2. 中国科学院计算技术研究所, 北京 100190;
3. 上海科技大学信息科学与技术学院, 上海 201210
2. Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, China;
3. School of Information Science and Technology, ShanghaiTech University, Shanghai 201210, China
物体检测是计算机视觉中一个重要的前置性任务,是指在图像或视频中给出物体的位置及对应的类别。因此物体检测包括2个子任务:定位物体的位置和识别物体的类别。近年来,物体检测领域取得显著进展,出现了若干具有代表性的物体检测方法[1-4],在若干个基准检测数据集上也取得越来越好的结果。但是对于未出现过的物体,例如使用不包含类别“dog”的训练集训练的物体检测模型,对如图 1所示的图片,则无法检测到“dog”这一类别,但却将检测框误判为“horse”、“sheep”或“cat”等这些训练集中出现过并且视觉特征比较相似的类别。这一现象表明,这类方法无法解决开放场景中的物体检测问题。究其原因,在于这些方法受限于训练集中的类别数量(Pascal VOC[5] 20类、MS COCO[6] 80类),试图以有限训练集应对无限开放世界是不可能的,由此必须另辟蹊径应对开放场景中的物体检测。图 1的现象也表明,对定位和识别2个子任务而言,前者具有更好的普适性,迁移相对容易,而识别任务因检测算法设计的原因,相对比较困难。

|
Download:
|
| 图 1 以往方法使用不包含类别“dog”的训练集训练得到检测器在包含“dog”类上的检测结果 Fig. 1 Detected results with previous object detection method and trained without "dog" | |
注意到人类应对开放场景的特点——当识别新的物体类别时,通常人们不仅仅依赖于其表观信息,而且还会借鉴日常生活以及学习过程中获取的先验知识。这得益于人们可以自动对不同的类别按照相似程度进行概念抽象,并形成层次化的类别结构,进而完成对未知类别的归类与识别。对未见过“dog”的人们可以基于已有先验知识,将图 1中的“dog”归类为一种与“horse”、“sheep”、“cat”相似的“quadruped”或者“animal”。因此可利用类似的层次化类别结构作为先验知识,通过有效的引导和约束深度网络,将检测的粒度加大,从而解决已往检测方法中识别子任务在未知类上迁移困难的问题。受上述过程的启发,本文提出一种尽力而为的物体检测方法。该方法可利用类别间的层级信息对检测到的未知物体识别或归类到虽不精确却一般且正确的类别,即将图 1的“dog”识别为“quadruped”,虽不精确但相对正确的较粗粒度类别,这种检测结果比图 1中以往方法的检测结果更准确。
已有物体检测方法在识别子任务的损失函数因仅考虑已知类别,通常将识别子任务看为一个多分类问题(softmax loss)或多个二分类问题(BCE loss)。正因如此,虽然在区域候选网络(RPN,region-proposal-network)阶段会产生多个未知类的候选区域(region of interest,RoI),但识别阶段却将此类候选区域丢弃或错误识别为已知类别。事实上,很多已有物体检测方法关注已知多个类别之间的判别性,而我们认为对没有训练数据的未知类,可利用简单的层级信息从多个已知类中蒸馏出超类信息进而泛化到未知类,这样的泛化对未知类检测更加重要。通常建模分布可以很好地在表达某个类别的同时兼具一定的泛化性,所以我们提出高斯层级损失(Gaussian hierarchical loss,GHL)。具体讲,假设层级结构上的每个类别服从多维高斯分布,模型不仅学习已知类别的分布情况,而且学习已知类中蒸馏出的超类分布。另外,使用KL散度(Kullback-Leibler divergence)显式地描述类别间的层级关系,增强超类在未知类上的泛化性,从而获得从已知类到未知类的迁移能力。本文通过实验验证了所提方法可在保持位置迁移性的前提下,增强模型识别未知物体的能力。
1 相关工作 1.1 通用物体检测基于深度学习的物体检测方法大致可分为2类。一类是基于候选区域RoI的两阶段方法,此类方法由Girshick等[7]在R-CNN中首次提出。两阶段检测器首先产生可能存在物体的候选区域,然后对每个候选区域进行分类。R-CNN利用底层的视觉信息产生候选框[8-9],随后将每个候选框区域内的图像分别送入卷积网络中计算,但这样造成很多冗余计算。之后,SPP-Net[10]和Fast-RCNN[1]使用候选区域池化层(RoI pooling)从卷积特征图中提取候选框的特征。为了可以进行端到端的训练,Faster-RCNN[2]引入RPN通过预定义的候选框(anchor boxes)增强产生候选框的效率。R-FCN[11]则通过限制某些通道表达的位置信息,将全连接子检测网络替换成全卷积层子检测网络,进一步提高了检测的效率。另一类不基于候选框的方法称为一阶段的方法,此类方法一般采用一个多任务网络,在对物体分类的同时回归物体的位置。YOLO[3]使用卷积网络直接预测物体的坐标和类别的概率,因位置参数更新范围较大,导致YOLO的检测精度比较差,所以YOLOv2[12]引入anchor box进一步提高精度。SSD[4, 13]、RetinaNet[14]进一步利用多尺度的特征。Anchor机制的引入增强了检测的精度,但其预定义的设置又成为发展的瓶颈,因此很多不依赖Anchor的方法[15-17]应运而生。另外,最近还有一些工作关注如何选取正负样例进行训练[14, 18],设置新的损失函数[14, 18-19]以及搜索合适的网络结构[20]等。
虽然很多方法在已有的检测数据集上都有不错的检测性能,但正如前文所述,大多方法因其根本缺陷对开放场景下的新类别检测依然束手无策,因此本文引入类别层级关系从更为一般的粒度上检测新类别。
1.2 类别层级关系在视觉中的应用作为人类先验知识的一种,类别间丰富的层级关系信息在很多视觉任务中有不错的表现。Srivastava和Salakhutdinov[21]尝试将类别间层级结构引入基于深度学习方法,主要利用类别间的层级关系在类别之间迁移知识,从而提高训练样本不足情况下的类别识别能力。HD-CNN[22]通过将深度神经网络嵌入一个类别层次结构,引入层次化的深度神经网络,使用粗糙的分类器识别简单类别,使用精细分类器识别困难类别。Ristin等[23]引入简单的层级结构主要关注提升子类的分类精度。层级信息还被用于多标签识别任务中,Deng等[24]提出使用层次-互斥图模型(hierarchy and exclusion graphs,HEX)利用类别间的关系辅助多标签分类,之后Ding等[25]进一步提出pHEX同样应用于多标签分类任务。另外层级信息还应用于细分类任务,Chen等[26]不但预测分类层级结构中各层级的类别,并将这种结构化关联信息集成到深度神经网络中,逐步约束标签的预测以及指导特征表达学习。Sfar等[27]集中关注于植物的细分类问题。Lee等[28]引入类别间的层级信息识别新的类别。
层级信息还应用于其他的视觉任务,Wu等[29]将层级结构关系利用到RGB图像的深度预测任务中。Zhang等[30]使用类别间的层级结构以及伴随类别的属性信息帮助图像检索任务。Wang等[31]关注自动图像注释,提出粒度感知分组概念,将语义相关的概念分组到不同的粒度级别,用以捕捉不同的人如何描述相同的图像内容变化。在小样本学习任务中,Li等[32]将源类和目标类之间的语义关系作为先验知识,通过源类和目标类的类别层次结构学习更具有可转移性的特征嵌入模型从而实现对目标类样本的识别。
鉴于类别间的层级信息可以辅助其他的非物体检测的视觉任务,所以我们利用类别间层级信息辅助开放场景下的物体检测任务。
1.3 层级物体检测为了应对检测数据集标注的检测类别过少的问题,YOLO9000[12]联合训练检测数据(MSCOCO[6])和分类数据(ImageNet[33]),在检测数据中学习物体位置定位,在分类数据中学习物体类别识别,通过引入WordNet[34]类别语义层级关系用于融合2种数据的标签,根据ImageNet中包含的概念建立分层树,对同一概念下的同义词进行分类。虽然YOLO9000[12]在对物体分类子任务中使用了类别的层级结构信息,但主要目的是利用分类数据增强检测类别的数量,可看作强监督检测和弱监督检测的融合。针对以上问题,本文提出利用类别的层级信息实现未知类别的检测。
2 高斯层级损失已有物体检测方法中,虽然RPN产生多个未知类的候选区域RoI,但识别阶段却将此类候选区域丢弃或误判为某个已知类别。因未知类没有训练数据,我们可通过类别间的层级信息从多个已知类中抽象出超类信息进而泛化到超类下的未知类别。
因此,不同于已有工作仅关注类别间判别性的损失函数,我们提出一种基于分布的识别损失——高斯层级损失,关注于如何描述已知类别和超类,在保证已知类别间判别性的同时使超类对所包含的未知类具有一定的泛化性。识别子任务的特征根据定位子任务阶段生成的每个RoI提取,在特征空间对每个类别进行高斯建模,同时对学习得到的特征空间进行层级约束。如图 2方法框架示意图所示,在模型刻画已知类“cat”和“dog”的同时,也刻画了超类“animal”的分布,因而未知类“sheep”的表现为符合超类“animal”的特征,但不同于“dog”和“cat”的特征。所以高斯层级损失学习描述已知类别的分布,同时从已知类中蒸馏出超类的分布,并加入KL散度进一步约束类别的层级关系,增强超类在未知类上的泛化性。未知类一般表现为:符合超类分布,但不同于其已知子类分布的样本。

|
Download:
|
| 图 2 基于高斯层级损失的检测方法示意图 Fig. 2 GHL based object detection | |
每个类别的图像分布都有其共性和相应的变化,很多工作,如Wan等[35]都曾使用统计分布建模这种类内的图像变化,本文将这种类内的图像变化建模成多维高斯分布,即假设每类由训练集图像样本获得的特征向量x服从式(1)表示的多维高斯分布:
| $ N(\boldsymbol{x} ; \boldsymbol{\mu}, \boldsymbol{\varSigma})=(2 {\rm{ \mathsf{ π} }})^{-\frac{d}{2}}|\boldsymbol{\varSigma}|^{-\frac{1}{2}} \mathrm{e}^{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}} \boldsymbol{\varSigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})}, $ | (1) |
其中:x为图像的特征,μ和Σ分别为其均值和方差。所以,对于样本xi是类别k的概率分布为
| $ \begin{gathered} p_{k}\left(x_{i}\right)=N\left(\boldsymbol{x}_{i} ; \boldsymbol{\mu}_{k}, \boldsymbol{\varSigma}_{k}\right) p\left(\boldsymbol{x}_{i} \in C_{k}\right)+ \\ \left(1-N\left(\boldsymbol{x}_{i} ; \boldsymbol{\mu}_{k}, \boldsymbol{\varSigma}_{k}\right)\right) p\left(\boldsymbol{x}_{i} \notin C_{k}\right), \end{gathered} $ | (2) |
其中:μk和Σk分别为类别k在特征空间的均值和协方差,Ck表示为类别k的集合,p(xi∈Ck)表示为类别k的先验概率。
在此假设下,在给定特征样本xi是否属于类别k的标签yik∈{0, 1}的条件下,特征xi的条件概率分布为
| $ p_{k}\left(\boldsymbol{x}_{i} \mid y_{i}^{k}=1\right)=N\left(\boldsymbol{x}_{i} ; \boldsymbol{\mu}_{k}, \boldsymbol{\varSigma}_{k}\right). $ | (3) |
因此,其后验概率分布可表示为
| $ p_{k}\left(y_{i}^{k} \mid \boldsymbol{x}_{i}\right)=\frac{N\left(\boldsymbol{x}_{i} ; \boldsymbol{\mu}_{k}, \boldsymbol{\varSigma}_{k}\right) p\left(\boldsymbol{x}_{i} \in C_{k}\right)}{p_{k}(\boldsymbol{x})}. $ | (4) |
为简化问题,假设各维独立,即协方差矩阵Σk是对角的,记为Λk;并假设先验概率p(xi∈Ck)=1/2。
如此,式(4)可重写为
| $ \begin{gathered} p_{i}^{k}=p_{k}\left(y_{i}^{k} \mid \boldsymbol{x}_{i}\right)=N\left(\boldsymbol{x}_{i} ; \boldsymbol{\mu}_{k}, \boldsymbol{\varLambda}_{k}\right)= \\ (2 {\rm{ \mathsf{ π} }})^{-\frac{d_{x_{i}}^{k}}{2}}\left|\boldsymbol{\varLambda}_{k}\right|^{-\frac{1}{2}} \mathrm{e}^{-d_{x_{i}}^{k}}, \\ d_{x_{i}}^{k}=\frac{1}{2}\left(\boldsymbol{x}_{i}-\boldsymbol{\mu}_{k}\right)^{\mathrm{T}} \boldsymbol{\varLambda}_{k}^{-1}\left(\boldsymbol{x}_{i}-\boldsymbol{\mu}_{k}\right), \end{gathered} $ | (5) |
其中:μk和Λk分别为均值和协方差矩阵。为使每个样本到同类的距离更近,到异类的距离更远,样本i在类别k上的分类损失为
| $ L_{i}^{k}=-\left[y_{i}^{k} \log \left(p_{i}^{k}\right)+\left(1-y_{i}^{k}\right) \log \left(1-p_{i}^{k}\right)\right]. $ | (6) |
相应地,分类损失定义为
| $ L_{\mathrm{cls}}=\frac{1}{N} \sum\nolimits_{i=1}^{N} \sum\nolimits_{k=1}^{K} L_{i}^{k}. $ | (7) |
为保证训练稳定,在具体实现中将常数项2π去掉,并使用sigmoid激活函数激活,从而得到样本i属于类别k的概率pik。
2.2 约束层级分布通过使用高斯分布建模类别分布得到的分类损失虽然可以衡量每个样本属于其类别的概率。但是,对某个超类的约束仅依赖其子类训练样本。因此,训练样本的多样性可使超类的分布具有更好的泛化能力,但仅优化分类损失不具有较强并且显示的类别层级关系。因每个类别单独学习,可能存在子类不符合超类表示的情况,即某个样本虽服从子类的分布,但并不服从超类的分布,如图 2中高斯建模得到的分布所示,“dog”分布的左上部分的样本以及“cat”右上部分的样本没有包含在“animal”类别分布中。因此,仅通过高斯分布建模得到的超类分布不具有较强的泛化性,从而影响未知类的识别,所以本文引入层级约束损失约束各类别分布具有层级关系的特点,最后得到如图 2右下角的分布。
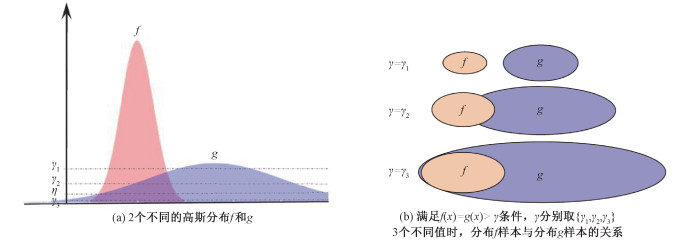
对于任意2个分布,如图 3(a)的f(左边)和g(右边),当γ取任意值时,在满足f(x)=g(x)>γ条件下,2个分布中样本x的关系应为图 3(b)所示的3种情况之一:当γ=γ1时,分布f和g的样本没有任何交集;当γ=γ2时,分布f和g的样本有部分交集;当γ=γ3时,分布f中的样本全部包含在g中。由图 3(b)可知,若使分布f和分布g的样本具有层级关系,则γ的取值范围为0≤γ≤η,随着γ取值的不同伴随着分布f和分布g包含程度的不同。
|
Download:
|
| 图 3 2个高斯分布及其不同阈值剖面 Fig. 3 Two Gaussian distributions and their profiles at different thresholds | |
因此,对于任意2个分布f和g,定义如下一种偏序关系:
| $ f ≼_{\gamma} g \Leftrightarrow\{x: f(x)>\gamma\} \subseteq\{x: g(x)>\gamma\}, $ | (8) |
其中{x: f(x)>γ}表示分布f大于阈值γ的所有样本集合,式(8)可表示为:在当且仅当g的样本集合包含f中的所有样本时,称g在γ程度下包含f。在式(8)中,分布g可以表示为超类的分布,分布f可以表示为子类的分布。
为使分布f和g具有层级关系,如果针对偏序关系
KL散度作为散度的一种,对于分布f和g,其KL散度为
| $ \mathrm{KL}(f \| g) \equiv \int f(x) \log \frac{f(x)}{g(x)} \mathrm{d} x. $ | (9) |
由式(9)可知,如果:
1) 样本x在分布f上具有较高概率,而在分布g上较低时,KL(f‖g)得一个较大的值,对应图 3分布f中与g不相交的样本,这种度量惩罚包含在f但不包含在g的样本,即如果分布f不被g所包含,KL散度会给予很高的惩罚。
2) 样本x在分布f上具有较低的概率值,而在分布g上较高时,KL(f‖g)是一个较小的值,这对应分布在f中与g相交的样本,即如果分布f被包含于g,KL散度给予的惩罚很小或为0。
因此当分布f=g时,KL(f‖g)=0;当f≠g且f≼g时,KL(f‖g)给予的惩罚较小,所以KL(f‖g)作为惩罚函数可约束分布f和g具有层级关系。
对于d维的高斯分布f=Nd(μf, Σf)和分布g=Nd(μg, Σg),KL散度表示为
| $ \begin{gathered} D_{\mathrm{KL}}(f \| g)=\frac{1}{2}\left(\log \left(\frac{\operatorname{det}\left(\boldsymbol{\varLambda}_{\mathrm{g}}\right)}{\operatorname{det}\left(\boldsymbol{\varLambda}_{f}\right)}\right)-d+\right. \\ \left.\operatorname{tr}\left(\boldsymbol{\varLambda}_{g}^{-1} \boldsymbol{\varLambda}_{f}\right)+\left(\boldsymbol{\mu}_{f}-\boldsymbol{\mu}_{g}\right)^{\mathrm{T}} \boldsymbol{\varLambda}_{g}^{-1}\left(\boldsymbol{\mu}_{f}-\boldsymbol{\mu}_{g}\right)\right). \end{gathered} $ | (10) |
所以,对于样本i,定义层级约束损失为
| $ \left.L_{\mathrm{KL}}=\max \left(0, \sum\nolimits_{f \in A_{k}^{i}, g \in A_{k}^{i}} D_{\mathrm{KL}}(f \| g)\right)\right), \text { s.t. } f ≼ g. $ | (11) |
其中,Aki为样本i所属类别k及其所有祖先类别节点的分布。
2.3 高斯层级损失分类损失Lcls主要约束样本识别为其类别及其祖先节点类别的概率可能性更高,层级约束损失LKL约束超类与其子类的分布具有更强的相似性,所以定义高斯层级损失LGH为
| $ L_{\mathrm{GH}}=L_{\mathrm{cls}}+\lambda L_{\mathrm{KL}}. $ | (12) |
其中λ为非负加权系数。
3 实验验证在本节中,通过在典型的物体检测数据集上进行的对比实验,验证提出的方法相对于以往方法的优越性。另外,通过消融实验验证所提出的层级高斯损失中各个损失的有效性,并对超参数的选取进行对比试验。
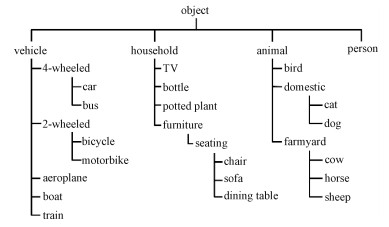
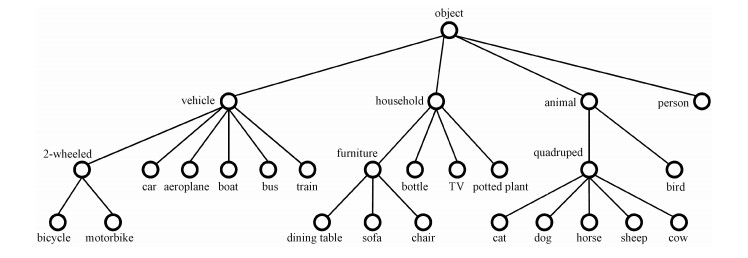
3.1 实验设置 3.1.1 层级结构建立基于Pascal VOC数据集的原始层级结构如图 4所示,原始层级结构仅利用语义信息,并未考虑类别在视觉上的相似性,以“domestic”超类和“farmyard”超类为例,虽然语义属于2个不同的类别,但若考虑形状和边缘信息的情况下,其子类在视觉上仍有很高的相似度,比如,“domestic”的子类“dog”和“farmyard”的子类“sheep”等。所以,基于视觉的相关信息,我们将层级结构调整为如图 5所示。
|
Download:
|
| 图 4 Pascal VOC原始类别层级树 Fig. 4 Original hierarchical category tree in Pascal VOC | |
|
Download:
|
| 图 5 Pascal VOC结合视觉信息调整后的类别层级树 Fig. 5 Modified hierarchical category tree with appearance constraint in Pascal VOC | |
采用Pascal VOC数据集的评测标准mAP(交并比IoU>0.5,intersection-over-union)作为评价指标。理想情况下,传统的物体检测方法检测不到未知的类别,但存在很多正确检测到框但误判为已知类别的检测结果,因此可基于重新构建的层级结构,将未知类别的兄弟类别检测结果作为未知类别的检测结果,从而计算未知类别的mAP。以图 5中的已知类别“dog”为例,以“dog”类别的兄弟类别(“cat”、“horse”和“sheep”)的检测结果作为未知类别“dog”的检测结果,从而计算“dog”的mAP值,本文中称之为Softmax_近似。本文实现的是尽力而为的检测,面对未知的类别,虽不能检测出具体未知类别,但其父节点类别包含了所有的未知类别,所以将父节点类别的检测结果作为未知类别的检测结果。同样以图 5中的未知类“dog”为例,将“quadruped”类别的检测结果作为未知类“dog”的检测结果。虽然YOLO9000[12]工作中提出的Softmaxtree层级分类损失未过多关注于未知类别的检测,但同样可实现超类的检测。另外使用多个Sigmoid二分类器同样也可实现超类的检测,所以这两种方法在一定程度上与本文提出方法具有类似的能力。
3.1.3 未知类别选取为模拟未见过的新类别,基于图 5的层级结构,分别在“vehicles”、“furniture”和“quadruped”这3个超类中随机选取2个、1个和2个类别作为未知类别。为验证所提出方法的有效性,排除选取不同未知类别对方法的影响,并保证对比的公平性,实验中选取了3种不同的未知类子集,具体如表 1所示。
|
|
表 1 3种不同未知类子集 Table 1 Three different subsets of unknown categories |
在Pascal VOC训练数据集中,选取仅包含已知类别实例,不含任何未知类别实例的图片作为训练子集。主要考虑2方面因素:一是问题的设定——提出的方法关注未知类别的检测,在训练集中不应直接出现包括图像在内的未知类别的任何信息;二考虑检测方法,在判断候选框是否包含物体时,需计算候选框与标注框的交并比IoU,当IoU大于某个阈值(如0.7)时,则此候选框为正例,当小于某个阈值(如0.3)则是负例。假设训练集中存在未知类别的实例,由于在此区域内没有正例标注框,在训练过程中会强制作为背景,产生误导行为,所以训练集中不含有任何未知类别实例的图片。
3.2 维度的影响因方法基于每个类别符合多维高斯分布的假设,所以维度数量作为一个可设置的超参数。在本节中,使用第1种未知类选取(子集1),VOC07trainval为训练集,在VOC07test数据集上测试不同的维度对检测结果的影响,不同维度的检测精度和召回率的结果如表 2所示。
|
|
表 2 高斯模型维度对检测精度和召回率的影响 Table 2 Dimensional factors on detection accuracy and recall with Gaussian model |
从表 2可以看出,不同维度的选取对AP影响比较大,但对RC的影响不大,而且不同超类偏好不同的维度——例如,“furniture”和“quadruped”在32维时对未知类的迁移性更强;“vehicles”类别则在使用16维的高斯分布建模时对未知类的迁移性已达到最好,后续维度的增加反而带来性能的下降。
其次,通过不同列AP的数值可以看出不同超类的数值差异比较大,数值大小关系为“quadruped”>“vehicles”>“furniture”。直观上,超类中包括的子类的差异性不同,因此各超类中已知类到未知类的迁移性难度也应不同,比如,超类“furniture”中从“dining table”类别和“chair”类别迁移到“sofa”类别,已知类与未知类的差异性较大,迁移较难;超类“quadruped”中从“cat”,“horse”和“sheep”3个类别迁移到“dog”和“cow”类别,“vehicles”超类中从“aeroplane”、“boat”和“bus”到“car”和“train”类别迁移,这2个超类对比“furniture”的迁移任务难度相对简单。虽不同超类AP的大小关系符合人们直观上对3个不同超类迁移困难度的理解,但不能排除方法的因素,所以数值的大小不能反映3个超类迁移困难的大小。但是,联合不同列的RC数值可以看出,3个超类RC的关系是”quadruped”>”furniture”>“vehicles”,但是AP的关系是”quadruped”>“vehicles”>”furniture”,可以看出相比超类“vehicles”,超类“furniture”候选框的噪声较多,识别难度更大。
3.3 层级约束有效性验证本节实验中,通过改变式(12)中λ的取值验证层级约束的有效性。为了对比的公平性,每个类别使用8维的高斯分布建模,实验结果如表 3所示。从表 3中第1行结果(λ=0,即没有引入层级约束)和其他几行的对比可以看到,除“furniture”超类在λ=1和λ=100时比不使用层级约束时性能有些许下降外,其他情况下层级约束的使用均带来不同程度的性能提升。所以,整体上使用层级约束可以增强已知类到未知类的迁移性或超类的泛化性。同时已知类的性能随λ增大得到了一定的提升,但约束过强会有些下降的趋势。
|
|
表 3 层级约束强度(公式(12)中λ)对检测精度和召回率的影响(VOC07test) Table 3 Affection of hierarchical Gaussian loss (λ in eq. (12)) on detection accuracy and recall (VOC07test dataset) |
为验证所提出方法的有效性,与检测方法中已有的损失函数在Pascal VOC数据集上进行对比实验。具体对比的方法有Softmax、Softmax_近似、Sigmoid和Softmaxtree[12],使用3.1节提到的评价方法和指标,实验结果如表 4和表 5所示。
|
|
表 4 与已有方法在VOC07test上的对比(使用VOC07trainval子集训练) Table 4 Comparison on VOC07test subset (training with VOC07trainval subset) |
|
|
表 5 与已有方法在VOC07test上的对比(使用VOC07trainval+VOC2012trainval子集训练) Table 5 Comparison on VOC07test subset (training with VOC07trainval+VOC2012trainval subsets) |
综合3个不同子集的结果,本文方法在未知类的检测精度上比已有的Sigmoid损失和Softmaxtree损失在VOC07训练集上平均分别提高5.4和5.7个百分点,在VOC07和VOC12训练集上平均分别提高5.6和6.4个百分点,验证了所提出的方法可更好地抽象出超类特征。
一个有趣的结果是不同方法在3个超类上的AP表现出类似相对性能趋势,即“quaruped”>“vehicles”>“furniture”。这很好地说明3个超类中已知类到未知类的迁移难度是不同的。另外,所提出的方法在“quadruped”和“vehicles”2个超类上都有明显的提升,而在“furniture”超类上本文所提出的方法与已有的方法大致相当,尤其在VOC07和VOC12训练集的结果中,这一现象与“furniture”超类内部各类别差异更大是直接相关的,从而迁移的难度更大。
同时注意到不同方法在3个子集划分上的性能表现也非常一致,AP值依次为:子集1>子集2>子集3,这一现象一方面说明3种划分的任务难度是不同的,同时说明所提出方法是稳定的。
从表 4和表 5的对比还可以看出,虽然不同数据集上结果的变化趋势略有,但整体上训练样本的增加有助于未知类检测任务性能的提升。
图 6给出本文方法与已有方法在未知类上检测的部分可视化结果。

|
Download:
|
| 图 6 所提出方法与以往方法在未知类上的检测结果 Fig. 6 The detection results of proposed method and existing methods on unknown categories | |
针对以往物体检测方法因受限于训练数据类别限制无法检测新类别的问题,本文从识别任务在已知类迁移到未知类过程中的问题出发,提出一种基于类别层次关系辅助未知类识别的方法,即高斯层级损失。在通用的物体检测评测数据集的实验表明,所提出的方法可在不损失已知类别性能的情况下,在未知类的检测中达到了目前最好的水平。
| [1] |
Girshick R. Fast R-CNN[C]//IEEE International Conference on Computer Vision: Santiago, Chile: IEEE Press, 2015: 1440-1448.
|
| [2] |
Ren S Q, He K M, Girshick R, et al. Faster R-CNN: Towards real-time object detection with region proposal Networks[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2017, 39(6): 1137-1149. |
| [3] |
Redmon J, Divvala S, Girshick R, et al. You only look once: unified, real-time object detection[C]//IEEE Conference on Computer Vision and Pattern Recognition: Las Vegas, USA: IEEE Press, 2016: 779-788.
|
| [4] |
Liu W, Anguelov D, Erhan D, et al. SSD: single shot multibox detector[C]//European Conference on Computer Vision: Amsterdam, The Netherlands: Springer International Publishing, 2016: 21-37.
|
| [5] |
Everingham M, Gool L V, Williams C K I, et al. The pascal visual object classes (VOC) challenge[J]. International Journal of Computer Vision, 2010, 88(2): 303-338. Doi:10.1007/s11263-009-0275-4 |
| [6] |
Lin T Y, Maire M, Belongie S, et al. Microsoft COCO: common objects in context[C]//European Conference on Computer Vision: Zurich, Swiss: Springer International Publishing, 2014: 740-755.
|
| [7] |
Girshick R, Donahue J, Darrell T, et al. Rich feature hierarchies for accurate object detection and semantic segmentation[C]//IEEE Conference on Computer Vision and Pattern Recognition: Columbus, USA: IEEE Press, 2014: 580-587.
|
| [8] |
Uijlings J, Sande K, Gevers T, et al. Selective search for object recognition[J]. International Journal of Computer Vision, 2013, 104(2): 154-171. Doi:10.1007/s11263-013-0620-5 |
| [9] |
Zitnick C, Doll'ar P. Edge boxes: locating object proposals from edges[C]//European Conference on Computer Vision: Zurich, Swiss: Springer International Publishing, 2014: 391-405.
|
| [10] |
He K M, Zhang X Y, Ren S Q, et al. Spatial pyramid pooling in deep convolutional networks for visual recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1904-1916. Doi:10.1109/TPAMI.2015.2389824 |
| [11] |
Dai J F, Li Y, He K M, et al. R-FCN: object detection via region-based fully convolutional networks[C]//Neural Information Processing Systems: Barcelona, Spain: 2016: 379-387.
|
| [12] |
Redmon J, Farhadi A. YOLO9000: better, faster, stronger[C]//IEEE Conference on Computer Vision and Pattern Recognition: Honolulu, USA: IEEE Press, 2017: 6517-6525.
|
| [13] |
闫凯, 沈汀, 陈正超, 等. 基于深度学习的SSD模型尾矿库自动提取[J]. 中国科学院大学学报, 2020, 37(3): 360-367. |
| [14] |
Lin T Y, Goyal P, Girshick R, et al. focal loss for dense object detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(2): 318-327. Doi:10.1109/TPAMI.2018.2858826 |
| [15] |
Zhu C C, He Y H, Savvides M. Feature selective anchor-free module for single-shot object detection[C]//IEEE Conference on Computer Vision and Pattern Recognition: Long Beach, USA: IEEE Press, 2019: 840-849.
|
| [16] |
Tian Z, Shen C H, Chen H, et al. FCOS: fully convolutional one-stage object detection[C]//IEEE International Conference on Computer Vision: Seoul, Korea: IEEE Press, 2019: 9627-9636.
|
| [17] |
Kong T, Sun F C, Liu H P, et al. FoveaBox: beyound anchor-based object detection[J]. IEEE Transactions on Image Processing, 2020, 29: 7389-7398. Doi:10.1109/TIP.2020.3002345 |
| [18] |
Pang J M, Chen K, Shi J P, et al. Libra R-CNN: towards balanced learning for object detection[C]//IEEE Conference on Computer Vision and Pattern Recognition: Long Beach, USA: IEEE Press, 2019: 821-830.
|
| [19] |
He Y H, Zhu C C, Wang J R, et al. Bounding box regression with uncertainty for accurate object detection[C]//IEEE Conference on Computer Vision and Pattern Recognition: Long Beach, USA: IEEE Press, 2019: 2888-2897.
|
| [20] |
Guo J Y, Han K, Wang Y H, et al. Hit-Detector: hierarchical trinity architecture search for object detection[C]//IEEE Conference on Computer Vision and Pattern Recognition: Seattle, USA: IEEE Press, 2020: 11405-11414.
|
| [21] |
Srivastava N, Salakhutdinov R. Discriminative transfer learning with tree-based priors[C]//Neural Information Processing Systems: Harrahs and Harveys, Lake Tahoe, USA: 2013: 2094-2102.
|
| [22] |
Yan Z C, Zhang H, Piramuthu R, et al. HD-CNN: hierarchical deep convolutional neural networks for large scale visual recognition[C]//IEEE International Conference on Computer Vision. Santiago, Chile: IEEE Press, 2015: 2740-2748.
|
| [23] |
Ristin M, Gall J, Guillaumin M, et al. From categories to subcategories: large-scale image classification with partial class label refinement[C]//The IEEE Conference on Computer Vision and Pattern Recognition: Boston, USA: IEEE Press, 2015: 231-239.
|
| [24] |
Deng J, Ding N, Jia Y P, et al. Large-scale object classification using label relation graphs[C]//European Conference on Computer Vision: Zurich, Swiss: Springer International Publishing, 2014: 48-64.
|
| [25] |
Ding N, Deng J, Murphy K, et al. Probabilistic label relation graphs with Ising models[C]//IEEE International Conference on Computer Vision: Santiago, Chile: IEEE Press, 2015: 1161-1169.
|
| [26] |
Chen T S, Wu W X, Gao Y F, et al. Fine-Grained representation learning and recognition by exploiting hierarchical semantic embedding[C]//The 26th ACM International Conference on Multimedia. New York, USA: ACM Press, 2018: 2023-2031.
|
| [27] |
Sfar A, Boujemaa N, Geman D. Confidence sets for fine-grained categorization and plant species identification[J]. International Journal of Computer Vision, 2015, 111(3): 255-275. Doi:10.1007/s11263-014-0743-3 |
| [28] |
Lee K, Lee K, Min K, et al. Hierarchical novelty detection for visual object recognition[C]//IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE Press, 2018: 1034-1042.
|
| [29] |
Wu C X, Lenz I, Saxena A. Hierarchical semantic labeling for task-relevant RGB-D perception[C]//Robotics: Science and Systems: Berkeley, USA: 2014: 1-9.
|
| [30] |
Zhang H W, Zha Z J, Yang Y, et al. Attribute-Augmented semantic hierarchy[C]//ACM Transactions on Multimedia Computing, Communications and Applications, 2014, 11(1s): 1-21.
|
| [31] |
Wang J, Yan F, Aker A, et al. A poodle or a dog? Evaluating automatic image annotation using human descriptions at different levels of granularity[C]//Third Workshop on Vision and Language: Dublin, Ireland: Dublin City University and the Association for Computational Linguistics, 2014: 38-45.
|
| [32] |
Li A X, Luo T G, Lu Z W, et al. Large-Scale Few-Shot learning: knowledge transfer with class hierarchy[C]//IEEE Conference on Computer Vision and Pattern Recognition: Long Beach, USA: IEEE Press, 2019: 7212-7220.
|
| [33] |
Russakovsky O, Deng J, Su H, et al. ImageNet large scale visual recognition challenge[J]. International Journal of Computer Vision, 2015, 115(3): 211-252. Doi:10.1007/s11263-015-0816-y |
| [34] |
Miller G A, Beckwith R, Fellbaum C, et al. Introduction to WordNet: an on-line lexical database[J]. International Journal of Lexicography, 1990, 3(4): 235-244. Doi:10.1093/ijl/3.4.235 |
| [35] |
Wan W T, Zhong Y Y, Li T P, et al. Rethinking feature distribution for loss functions in image classification[C]//IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA: IEEE Press, 2018: 9117-9126.
|
 2021, Vol. 38
2021, Vol. 38 


