在卫星导航定位解算中,通常釆用最小二乘法(least square method, LSM)[1-2],其思想是在含有误差与噪声的各个测量值之间寻求一个最优值,使得所有测量值的残差平方和最小。因为由定位方程解算出的坐标值与伪距测量值是非线性关系,为便于计算,使用最小二乘法之前需要对定位方程组进行线性化展开,舍去高阶项,其代价是会造成截断误差;同时最小二乘法只使用当前历元的伪距测量值,定位结果受测量噪声影响较大。从一系列伪距测量值中确定位置的问题可以表示为一个滤波问题,因此可以借鉴卡尔曼滤波的思想[3],通过用最新的测量值更新过去位置的估计值递归地估计当前位置,可以获得更加稳定的位置估计结果。但经典卡尔曼滤波通常只适用于线性系统,为解决非线性系统的滤波问题,可以对非线性系统进行线性化,即扩展卡尔曼滤波(extended Kalman filter, EKF)[3]。但EKF也是通过舍去高阶项对非线性系统进行近似,同样会引入高阶项截断误差,只能达到一阶精度。
容积卡尔曼滤波(cubature Kalman filter, CKF)[4]是Arasaratnam I和Haykin S在2009年提出的基于贝叶斯估计和容积变换的一种非线性滤波方法。它将高斯域非线性滤波问题归结为求解非线性函数和高斯概率密度乘积的数值积分[4-6],计算出一组具有相同权重的点,并直接通过非线性系统方程对系统状态和误差进行递推估计,其精度可以达到三阶以上[7],在非线性滤波领域得到越来越多的应用[5-12]。
1 容积卡尔曼滤波 1.1 贝叶斯估计在实际应用中,不论是线性系统还是非线性系统,其状态估计问题都可以用贝叶斯估计来描述。贝叶斯估计[6]的核心思想是:利用已知系统初始状态概率密度和系统测量值,以递推的方式求得状态后验概率密度函数。状态后验概率密度函数可以描述非线性系统的统计特性,求得后验概率密度函数就意味着得到了系统的最优估计。递推估计的过程可以看作是滤波的过程,主要目的是将系统的状态通过包含噪声的观测量估计出来。对于线性系统而言,最优滤波估计就是经典卡尔曼滤波;但对于非线性系统, 由于需要进行无穷维积分运算[6],使得最优估计无法实现。为此人们提出大量次优的近似非线性滤波方法,如扩展卡尔曼滤波、无迹卡尔曼滤波和容积卡尔曼滤波等。
在实际中高斯分布是最常见且应用最广泛的分布,因此本文重点针对高斯域的估计问题。高斯域非线性离散系统模型[4-6, 12]如下:
| $ \boldsymbol{x}_{k} =f\left(\boldsymbol{x}_{k-1}\right)+w_{k-1}, $ | (1) |
| $ \boldsymbol{z}_{k} =h\left(\boldsymbol{x}_{k}\right)+v_{k-1}, $ | (2) |
式中:xk为系统状态向量;zk为测量向量;f为系统非线性状态转移函数;h为测量函数;wk为系统状态转移噪声;vk为测量噪声。wk和vk均为高斯白噪声且不相关。式(1)和式(2)分别表示系统包含的2个随机过程:状态转移和测量。系统状态估计的目的是利用含有噪声的测量信息估计系统状态xk,即从式(2)描述的测量方程结合式(1)状态转移方程递推估计xk。
将系统状态转移模型和测量模型概率化,则对高斯域非线性离散系统模型式(1)和式(2)的状态估计[4-5, 13]一般形式如下:
| $ \left\{\begin{array}{l} \boldsymbol{x}_{k \mid k}=\hat{\boldsymbol{x}}_{k \mid k-1}+\boldsymbol{L}_{k}\left(\boldsymbol{z}_{k}-\hat{\boldsymbol{z}}_{k}\right), \\ \boldsymbol{P}_{k \mid k}=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{L}_{k} \boldsymbol{P}_{z z} \boldsymbol{L}_{k}^{\mathrm{T}}, \\ \boldsymbol{L}_{k}=\boldsymbol{P}_{x z} \boldsymbol{P}_{z z}^{-1} . \end{array}\right. $ | (3) |
式中:Pk|k为状态转移误差协方差矩阵;Pk|k-1为一步预测误差协方差矩阵;Lk为卡尔曼增益;Pzz为测量自相关协方差矩阵;Pxz为状态测量互相关协方差矩阵。上述变量具体计算可归结为求解形如“非线性函数×高斯概率密度”的函数的积分问题[4-5, 13],如下所示
| $ \int\limits_{R^{n}} f(\boldsymbol{x}) \exp \left(-\boldsymbol{x}^{\mathrm{T}} \boldsymbol{x}\right) \mathrm{d} \boldsymbol{x}. $ | (4) |
式中: x为积分向量;f(x)为非线性函数;Rn为积分区域,即n维实向量空间。一般情况下,式(4)所示积分的解析值无法得到,需用近似方法获得其解析值的近似解。采用不同的数值积分近似算法就可以推导出高斯域各种非线性近似滤波算法。
1.2 球面-径向容积准则CKF是根据贝叶斯估计理论及“球面-径向”容积(spherical-radial cubature)准则得出的滤波算法,使用一组容积点逼近具有附加高斯噪声的非线性系统的状态均值和误差协方差,可以有效地解决非线性系统的状态估计问题[4-6]。
| $ \int\limits_{\mathbb{R}^{n}} f(x) \exp \left(-\boldsymbol{x}^{\mathrm{T}} \boldsymbol{x}\right) \mathrm{d} \boldsymbol{x} \approx \frac{\sqrt{{\rm{ \mathsf{ π} }}^{n}}}{2 n} \sum\limits_{i=1}^{2 n} f\left(\sqrt{\frac{n}{2}}[1]_{i}\right), $ | (5) |
其中,n为系统状态向量维数。
| $ [1]=\left[\begin{array}{cccccc} 1 & \cdots & 0 & -1 & \cdots & 0 \\ \vdots & & \vdots & \vdots & & \vdots \\ 0 & \cdots & 1 & 0 & \cdots & -1 \end{array}\right]. $ | (6) |
其中,[1]i表示矩阵[1]的第i列。
对标准高斯分布函数f(x)求解积分IN(f)
| $ I_{N}(f)=\int\limits_{\mathbb{R}^{n}} f(x) N(\boldsymbol{x} ; 0, \boldsymbol{I}) \mathrm{d} \boldsymbol{x}. $ | (7) |
其中,N(x; 0, I)为f(x)的概率密度函数,表示f(x)满足均值为0、方差为单位阵I的高斯分布。因此式(7)可写为
| $ I_{N}(f)=\frac{1}{\sqrt{{\rm{ \mathsf{ π} }}^{n}}} \int\limits_{\mathbb{R}^{n}} f(\sqrt{2} \boldsymbol{x}) \exp \left(-\boldsymbol{x}^{\mathrm{T}} \boldsymbol{x}\right) \mathrm{d} \boldsymbol{x}, $ | (8) |
结合式(4)、式(5),式(8)可写为
| $ \begin{aligned} I_{N}(f) & \approx \frac{1}{\sqrt{{\rm{ \mathsf{ π} }}^{n}}}\left(\frac{\sqrt{{\rm{ \mathsf{ π} }}^{n}}}{2 n} \sum\limits_{i=1}^{2 n} f\left(\sqrt{2} \sqrt{\frac{n}{2}}[1]_{i}\right)\right) \\ &=\sum\limits_{i=1}^{m} \omega_{i} f\left(\xi_{i}\right). \end{aligned} $ | (9) |
其中
| $ \left\{\begin{array}{l} \xi_{i}=\sqrt{\frac{m}{2}}[1]_{i} ,\\ \omega_{i}=\frac{1}{m} ,\\ i=1, \cdots m ,\\ m=2 n . \end{array}\right. $ | (10) |
式中:ξi为容积点;ωi为权值;m为容积点数。
对于均值为μ、方差为∑的一般高斯分布函数f(x)求解积分
| $ \begin{aligned} I_{N}(f) &=\int\limits_{\mathbb{R}^{n}} f(x) N\left(\boldsymbol{x} ; \mu, \sum\right) \mathrm{d} \boldsymbol{x} \\ &=\int\limits_{\mathbb{R}^{n}} f\left(\sqrt{\sum \boldsymbol{x}} \boldsymbol{x}+\mu\right) N(\boldsymbol{x} ; 0, \boldsymbol{I}) \mathrm{d} \boldsymbol{x} \\ &=\sum\limits_{i=1}^{m} \omega_{i} f\left(\sqrt{\sum} \xi_{i}+\mu\right). \end{aligned} $ | (11) |
由以上推导可知,根据“球面—径向”容积准则,共选取2n个权值相等的容积点即可计算形如式(4)的积分。
1.3 容积卡尔曼滤波原理使用容积点集计算方程(3)中的各个参量,即可得出CKF递推公式,在每个滤波周期内进行时间更新和测量更新[4-6, 10]。
1) 时间更新
假设k-1时刻后验概率密度函数已知,通过Cholesky分解误差协方差矩阵Pk-1|k-1
| $ \boldsymbol{P}_{k-1 \mid k-1} =\boldsymbol{S}_{k-1 \mid k-1} \boldsymbol{S}_{k-1 \mid k-1}^{\mathrm{T}} . $ | (12) |
计算容积点(i=1, 2, …m, m=2n)
| $ X_{i, k-1 \mid k-1}= \boldsymbol{S}_{k-1 \mid k-1} \xi_{i}+\hat{\boldsymbol{x}}_{k-1 \mid k-1}, $ | (13) |
其中ξi见式(10)。
通过状态转移方程计算传播容积点
| $ X_{i, k \mid k-1}^{*}=f\left(X_{i, k-1 \mid k-1}\right) . $ | (14) |
根据式(11),估计k时刻的状态预测值
| $ \hat{\boldsymbol{x}}_{k \mid k-1}=\frac{1}{m} \sum\limits_{i=1}^{m} X_{i, k \mid k-1}^{*}. $ | (15) |
估计k时刻的状态误差协方差预测值
| $ \begin{aligned} \boldsymbol{P}_{k \mid k-1}=& \frac{1}{m} \sum\limits_{i=1}^{m} \boldsymbol{X}_{i, k \mid k-1}^{*} \boldsymbol{X}_{i, k \mid k-1}^{* \mathrm{~T}}-\\ & \hat{\boldsymbol{x}}_{k \mid k-1} \hat{\boldsymbol{x}}_{k \mid k-1}^{\mathrm{T}}+\boldsymbol{Q}_{k-1} . \end{aligned} $ | (16) |
其中Q为状态转移噪声协方差矩阵。
2) 测量更新
通过Cholesky分解Pk|k-1
| $ \boldsymbol{P}_{k \mid k-1}=\boldsymbol{S}_{k \mid k-1} \boldsymbol{S}_{k \mid k-1}^{\mathrm{T}}. $ | (17) |
计算容积点(i=1, 2, …m, m=2n)
| $ \boldsymbol{X}_{i, k \mid k-1}=\boldsymbol{S}_{k \mid k-1} \xi_{i}+\hat{\boldsymbol{x}}_{k \mid k-1}. $ | (18) |
通过测量函数h计算传播容积点
| $ \boldsymbol{Z}_{i, k \mid k-1}=h\left(\boldsymbol{X}_{i, k \mid k-1}\right) . $ | (19) |
估计k时刻的测量预测值
| $ \boldsymbol{\hat{z}}_{k \mid k-1}=\frac{1}{m} \sum\limits_{i=1}^{m} \boldsymbol{Z}_{i, k \mid k-1} . $ | (20) |
估计测量自相关协方差矩阵
| $ \begin{aligned} \boldsymbol{P}_{z z, k \mid k-1}=& \frac{1}{m} \sum\limits_{i=1}^{m} \boldsymbol{Z}_{i, k \mid k-1} \boldsymbol{Z}_{i, k \mid k-1}^{\mathrm{T}}-\\ & \boldsymbol{\hat{z}}_{k \mid k-1} \boldsymbol{\hat{z}}_{k \mid k-1}^{\mathrm{T}}+\boldsymbol{R}_{k} . \end{aligned} $ | (21) |
其中Rk为测量噪声协方差。
估计状态测量互相关协方差矩阵
| $ \boldsymbol{P}_{x z, k \mid k-1}=\frac{1}{m} \sum\limits_{i=1}^{m} \boldsymbol{X}_{i, k \mid k-1} \boldsymbol{Z}_{i, k \mid k-1}^{\mathrm{T}}-\hat{\boldsymbol{x}}_{k \mid k-1} \boldsymbol{\hat{z}}_{k \mid k-1}^{\mathrm{T}} . $ | (22) |
估计卡尔曼增益
| $ \boldsymbol{L}_{k}=\boldsymbol{P}_{x z, k \mid k-1} \boldsymbol{P}_{z z, k \mid k-1}^{-1}. $ | (23) |
k时刻状态估计值
| $ \hat{\boldsymbol{x}}_{k \mid k}=\hat{\boldsymbol{x}}_{k \mid k-1}+\boldsymbol{L}_{k}\left(\boldsymbol{z}_{k}-\hat{\boldsymbol{z}}_{k \mid k-1}\right) . $ | (24) |
k时刻状态误差协方差估计值
| $ \boldsymbol{P}_{k \mid k}=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{L}_{k} \boldsymbol{P}_{z z, k \mid k-1} \boldsymbol{L}_{k}^{\mathrm{T}} . $ | (25) |
式中
在卫星导航定位中,需要对接收机的5个状态进行估计:接收机三维位置坐标(xu, yu, zu)、接收机时钟偏差Δtu以及接收机时钟频率漂移Δfu。按照时间更新和测量更新2个环节进行估计。
1) 时间更新
根据式(10),容积点ξi及权值ωi分别为
| $ \left\{\begin{array}{l} \xi_{i}=\sqrt{5}[1]_{i}, \\ \omega_{i}=\frac{1}{10}, \\ i=1, \cdots 10. \end{array}\right. $ | (26) |
k时刻接收机位置坐标利用递推方式表示为
| $ \left[\begin{array}{c} x_{u}(k) \\ y_{u}(k) \\ z_{u}(k) \\ \Delta t_{u}(k) \\ \Delta f_{u}(k) \end{array}\right]=\left[\begin{array}{lllll} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & T \\ 0 & 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} x_{u}(k-1) \\ y_{u}(k-1) \\ z_{u}(k-1) \\ \Delta t_{u}(k-1) \\ \Delta f_{u}(k-1) \end{array}\right], $ | (27) |
则状态转移矩阵为
| $ \boldsymbol{F}=\left[\begin{array}{lllll} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & T \\ 0 & 0 & 0 & 0 & 1 \end{array}\right], $ | (28) |
式中T为观测历元时间间隔。
将式(26)、式(28)代入式(13)、式(14),即可计算时间更新环节传播容积点。
| $ \boldsymbol{Q}=\left[\begin{array}{ccccc} S_{\mathrm{P}} T & 0 & 0 & 0 & 0 \\ 0 & S_{\mathrm{P}} T & 0 & 0 & 0 \\ 0 & 0 & S_{\mathrm{P}} T & 0 & 0 \\ 0 & 0 & 0 & S_{\mathrm{f}} \frac{T^{3}}{3} & S_{\mathrm{f}} \frac{T^{2}}{2} \\ 0 & 0 & 0 & S_{\mathrm{f}} \frac{T^{2}}{2} & S_{\mathrm{f}} T \end{array}\right] . $ | (29) |
式中:SP为三维位置噪声功率谱密度,Sf为接收机时钟频率的噪声功率谱密度。
2) 测量更新
为确定接收机的位置坐标(xu, yu, zu),接收机需测量出自身与3颗卫星的距离ρ1、ρ2和ρ3。但由于接收机时钟与卫星时钟存在钟差Δtu(假设不同卫星之间的钟差为0),必须将钟差Δtu也作为1个未知数进行求解。因此,至少需要再增加1颗卫星参与测量,相应增加1个方程。实际中可视卫星数量往往多于4个,构成定位方程组
| $ \left\{\begin{array}{l} \rho_{1}=\sqrt{\left(x_{1}-x_{u}\right)^{2}+\left(y_{1}-y_{u}\right)^{2}+\left(z_{1}-z_{u}\right)^{2}}+c \cdot \Delta t_{u}, \\ \rho_{2}=\sqrt{\left(x_{2}-x_{u}\right)^{2}+\left(y_{2}-y_{u}\right)^{2}+\left(z_{2}-z_{u}\right)^{2}}+c \cdot \Delta t_{u}, \\ \rho_{3}=\sqrt{\left(x_{3}-x_{u}\right)^{2}+\left(y_{3}-y_{u}\right)^{2}+\left(z_{3}-z_{u}\right)^{2}}+c \cdot \Delta t_{u}, \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ \rho_{N}=\sqrt{\left(x_{N}-x_{u}\right)^{2}+\left(y_{N}-y_{u}\right)^{2}+\left(z_{N}-z_{u}\right)^{2}}+c \cdot \Delta t_{u}. \end{array}\right. $ | (30) |
式中:(xn, yn, zn)为卫星的三维坐标,N为可视卫星总数,c为光速。
式(30)即为式(19)中的测量函数h,根据式(19)、式(30),即可计算测量更新环节传播容积点。
假设接收机的伪距测量方差为σD2,根据卫星高度角不同,伪距测量精度会受到影响。考虑卫星高度角因素,伪距测量噪声协方差矩阵[14-15]为
| $ \boldsymbol{R}=\left[\begin{array}{cccc} \left(\frac{\sigma_{\mathrm{D}}}{\sin \theta_{n}}\right)^{2} & 0 & 0 & 0 \\ 0 & \left(\frac{\sigma_{\mathrm{D}}}{\sin \theta_{n}}\right)^{2} & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \left(\frac{\sigma_{\mathrm{D}}}{\sin \theta_{n}}\right)^{2} \end{array}\right]. $ | (31) |
式中,θn为第n颗卫星相对于接收机的高度角。根据以上参数,即可通过式(12)~式(25)递推估计接收机的位置坐标。
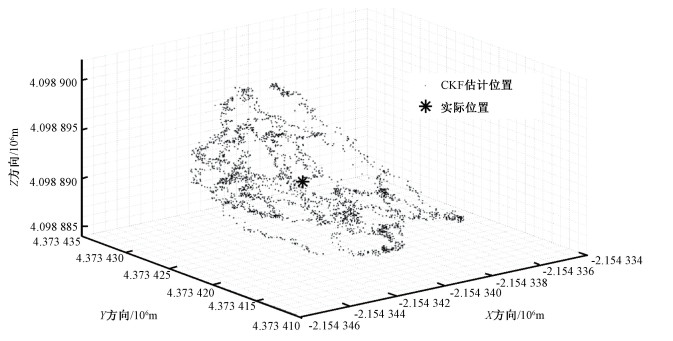
3 实测数据分析本文以静态三维定位为例,利用国际GNSS服务(International GNSS Service, IGS)官网提供的北京地区某GNSS监测站采集的GPS接收机测量的伪距及卫星星历数据,利用CKF算法估计GPS监测站接收机的三维位置坐标。系统参数设置如下:IGS监测接收机测量周期T=30 s;根据经验值,一般导航接收机伪距测量方差σD2=10 m2[11, 16];令接收机三维位置噪声功率谱密度SP=σD2/3;接收机时钟的频率噪声功率谱密度Sf= 10-12 [11, 16]。利用CKF算法估计的24 h GPS监测站接收机三维坐标如图 1所示。
|
Download:
|
| 图 1 CKF算法估计的三维坐标 Fig. 1 3-D coordinate estimated by CKF algorithm | |
对IGS监测接收机连续24 h的观测值, 利用CKF估计的结果与实际坐标偏差如图 2所示。

|
Download:
|
| 图 2 CKF算法估计结果与实际坐标偏差 Fig. 2 Deviation of CKF algorithm estimation result from the actual coordinates | |
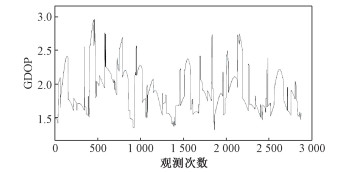
连续24 h可视的GPS卫星几何精度因子(geometric dilution precision, GDOP)如图 3所示。
|
Download:
|
| 图 3 24 h GDOP值 Fig. 3 GDOP for 24 h | |
基于同样的IGS监测站数据,分别用LSM、EKF和CKF 3种算法估计接收机三维坐标,3种算法定位偏差局部放大对比如图 4所示。

|
Download:
|
| 图 4 3种算法估计的定位偏差 Fig. 4 Positioning bias estimated by three algorithms | |
由图 4可见,EKF算法和CKF算法估计结果更加平缓,定位精度更高。由于初始坐标未知,接收机随机设置的初始坐标不准,EKF算法和CKF算法都需要经过震荡收敛,如图 5所示。

|
Download:
|
| 图 5 EKF与CKF估计收敛速度对比 Fig. 5 Comparison of convergence rates of EKF and CKF estimates | |
由图 5可见,随着滤波次数的增加,EKF和CKF坐标估计结果都可迅速收敛,而CKF比EKF具有更快的收敛速度。这是因为与EKF算法相比,由于基于贝叶斯估计和容积变换的CKF算法更适用于非线性的定位解算方程组,每次估计结果误差更小,因此定位解算结果可以更快地收敛。
在相同的场景下,对24 h的定位解算结果进行对比,3种算法估计位置坐标标准差结果如表 1所示。
|
|
表 1 3种算法估计误差对比 Table 1 Comparison of estimation errors of three algorithms |
可见,在定位解算的应用中,与传统的LSM算法相比,EKF算法和CKF算法可以获得更高的精度,CKF算法又优于EKF算法。
用Matlab对3种算法进行实现并进行测试,对全天2 880个观测历元的观测数据进行定位解算,3种算法的运行时间如表 2所示。
|
|
表 2 3种算法运行时间对比 Table 2 Comparison of running time of three algorithms |
由表 2可见,EKF算法的运算开销最少,而CKF算法由于涉及较多的矩阵变量,需要经过更多步骤的矩阵运算,因此运算量开销较大。综合性能与代价比较,在静态卫星导航定位解算中其经济性不如EKF算法。
4 结论本文将基于贝叶斯估计的非线性滤波方法CKF应用于导航定位解算。介绍CKF滤波算法的基本原理和递推过程,建立卫星导航定位解算的状态转移模型和测量误差模型。利用IGS实际观测数据进行验证,并与传统的LSM和EKF进行对比。结果显示:相比于LSM和EKF方法,CKF算法具有更高的导航定位解算精度,与EKF相比具有更好的收敛特性,为卫星导航定位提供了一种新的滤波解算途径。
| [1] |
Kaplan E D, Hegarty C. Understanding GPS: principles and applications[M]. 2nd edition. Norwood: Artech House, 2006: 322-332.
|
| [2] |
谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 96-106.
|
| [3] |
秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 2版. 西安: 西北工业大学出版社, 2012: 1-3.
|
| [4] |
Arasaratnam I, Haykin S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269. Doi:10.1109/TAC.2009.2019800 |
| [5] |
唐李军. Cubature卡尔曼滤波及其在导航中的应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [6] |
杨峻巍. 水下航行器导航及数据融合技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [7] |
Havlicek M, Jan J, Brazdil M, et al. Nonlinear estimation of BOLD signal based on cubature particle filter[C]//The 20th Int EURASIP Conf on BIOSIGNAL 2010. Brno, 2010: 328-332.
|
| [8] |
Roy A, Mitra D. Multi-target trackers using cubature Kalman filter for Doppler radar tracking in clutter[J]. IET Signal Processing, 2016, 10(8): 888-901. Doi:10.1049/iet-spr.2015.0540 |
| [9] |
葛磊. 容积卡尔曼滤波算法研究及其在导航中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [10] |
王宏健, 李村, 么洪飞, 等. 基于高斯混合容积卡尔曼滤波的UUV自主导航定位算法[J]. 仪器仪表学报, 2015, 36(2): 254-261. |
| [11] |
Pesonen H, Piché R. Cubature-based Kalman filters for positioning[C]//2010 7th Workshop on Positioning, Navigation and Communication (WPNC). Dresden, Germany: IEEE Press, 2010: 45-49.
|
| [12] |
Cui B B, Chen X Y, Tang X H. Improved cubature Kalman filter for GNSS/INS based on transformation of posterior sigma-points error[J]. IEEE Transactions on Signal Processing, 2017, 65(11): 2975-2987. Doi:10.1109/TSP.2017.2679685 |
| [13] |
Ito K, Xiong K. Gaussian filters for nonlinear filtering problems[J]. IEEE Transactions on Automatic Control, 2000, 45(5): 910-927. Doi:10.1109/9.855552 |
| [14] |
陈杨毅. GPS与BD双模GNSS接收机定位解算技术研究[D]. 厦门: 厦门大学, 2014.
|
| [15] |
Gao C F, Wu F, Chen W R, et al. An improved weight stochastic model in GPS Precise Point Positioning[C]//International Conference on Proceedings Transportation, Mechanical, and Electrical Engineering(TMEE). 2011 Changchun, China: IEEE Press, 2011: 629-632.
|
| [16] |
王慧, 王伟. 一种改进的卡尔曼滤波定位算法研究[J]. 船舶工程, 2006, 28(4): 34-38. Doi:10.3969/j.issn.1000-6982.2006.04.013 |
 2021, Vol. 38
2021, Vol. 38 


