2. 中国科学院大学, 北京 100049;
3. 上海科技大学, 上海 201210
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. ShanghaiTech University, Shanghai 201210, China
目前,MIMO(massive multi-input multi-output)雷达是雷达领域的研究热点[1-8]。MIMO雷达由多个不同的发射阵元天线和接收阵元天线组成。已有数学分析和实验仿真证明,MIMO雷达有很多潜在的优势[1-4]。例如提升检测性能、提高雷达自由度和估计精度等。MIMO雷达根据其天线布阵形式主要可以分为2大类:第1类是集中式MIMO雷达[5-6]。发射天线阵列和接收天线阵列之间紧凑分布。集中式MIMO雷达在发射端发射相互独立或正交的波形以获得波形分集特性,提升了系统的自由度[3, 6]。接收端通过波束成形技术来提高相干处理增益[5]。第2类是分布式MIMO雷达[7-8]。发射阵元和接收阵元之间相隔很远。分布式MIMO雷达由于阵元之间的位置分布较广,可以从多个不同的方向接收目标的后向散射回波,减轻目标的雷达横截面积(radar cross sections, RCSs)闪烁[3],提升检测性能[7]和估计精度[8]。
目标检测是雷达的一个重要功能。在干扰杂波相关性未知的情况下,分布式MIMO雷达的目标检测问题被广泛研究[1-3]。为了估计未知的协方差矩阵,一种常用的标准假设是有充足的训练数据。文献[9-10]在满足上述假设的前提下,在高斯杂波环境中利用抽样协方差矩阵方法设计一个新的检测器用于雷达目标检测。文献[11]将高斯杂波拓展为复合高斯分布,提出一种更鲁棒性的采样协方差矩阵检测器。实际雷达场景中,由于杂波频谱的快变性,很难得到充足的训练数据。文献[12]利用杂波协方差矩阵的斜对称结构减少对训练数据的依赖。上述算法都假设分布式MIMO雷达处于均匀性杂波环境中,即所有的发射-接收对的协方差矩阵都是相同的。文献[13]证明杂波特性与阵元所处位置具有强相关性,即发射-接收天线对的相对位置不同时,它们之间的杂波属性可能也具有差异。Gao等[14]在此基础上将杂波协方差矩阵建模为未知的随机矩阵,并模拟非均匀杂波环境,推导了基于知识辅助的GLRT检测器。由于以上算法仍然需要充足或者少量的训练数据,所以由于杂波快变性导致的训练数据不足的问题没有被完全解决。
此外,随着雷达分辨率的提升,当雷达距离分辨率小于目标尺寸时,目标回波可能占有多个距离单元。这将严重影响雷达的检测概率。因此,距离扩展目标检测已成为高分辨率雷达研究的重要课题。针对高斯白噪声中的距离扩展目标检测问题,文献[15]提出一种考虑目标散射体密度的广义似然比检测器(generalized likelihood ratio tests, GLRT);Maio和Orlando [16]将距离扩展目标检测问题转化为多秩子空间目标信号检测问题;Gao等[14]提出一种基于知识辅助的2步GLRT检测器,但是其计算耗时仍然很高;文献[17]研究非高斯杂波下扩展目标的检测问题,设计了一种基于知识辅助的Wald检测器;文献[18]将距离扩展目标建模为多级子目标信号进行处理。
针对杂波训练数据不足以及高分辨率雷达中距离扩展现象等问题,本文首先介绍分布式MIMO雷达对距离扩展目标检测的信号模型。将不同发送-接收对(Tx-Rx)所对应的干扰杂波协方差矩阵建模为随机矩阵。同时指定它们的先验分布为逆复Wishart分布,并通过设置不同发射-接收对的功率水平来模拟非均匀杂波环境。然后通过2步法设计2种新的贝叶斯检测器。首先,在假设协方差矩阵已知的情况下,推导出Rao和Wald检测器的表达式。然后利用先验信息分布,结合贝叶斯方法得到协方差矩阵的最大后验(MAP)估计量,并用该估计量对Rao和Wald检测器中的协方差矩阵进行替换,以此推导出的检测器不需要训练数据。仿真结果表明,本文设计的B-Rao(Bayesian-Rao)和B-Wald(Bayesian-Wald)检测器在检测性能上优于已存的抽样协方差矩阵SCM(sample-covariance-matrix)和鲁棒抽样协方差矩阵RSCM(robust-SCM)检测器,而与基于知识辅助的KA-GLRT检测器相比,检测性能相近,但是计算复杂度更低且不需要训练数据。
文中(·)*、(·)T和(·)†分别代表复共轭、转置和共轭转置。tr(·)代表矩阵的迹。exp(·)表示指数函数。|·|代表矩阵的行列式。I表示单位阵,符号“~
假设MIMO雷达的发射天线数和接收天线数分别为M和N。每个发射天线在一个相干处理间隔内发射L个脉冲,且发射天线之间发射的波形相互正交。在接收端,每个接收天线配备M个匹配滤波器,由于雷达的高分辨率,需要考虑距离扩展问题。假设一个目标可以扩展到H≥1个距离单元,那么在第n个接收天线关于第m个发射天线的匹配滤波器输出可以表示为
| $ \left\{\begin{array}{l} H_{0}: \boldsymbol{X}_{m n}=\boldsymbol{N}_{m n}, \\ H_{1}: \boldsymbol{X}_{m n}=\boldsymbol{\alpha}_{m n} \boldsymbol{p}_{\mathrm{r}, m n} \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m}+\boldsymbol{N}_{m n}. \end{array}\right. $ | (1) |
Sm是第m个发射天线发射的波形,αmn=[αmn, 1, …, αmn, H]T表示距离扩展目标的未知幅度参数。其中:
Nmn=[nmn, 1, …, nmn, H]表示干扰,可能包含杂波和热噪声。且假设Nmn的每一列都是独立同分布于零均值复高斯分布,即nmn, h~CN(0, Rmn), h=1, …, H。其协方差矩阵Rmn在不同的发射接收对之间互不相同。
传统求解上述问题的方法是假设协方差矩阵R为未知但确定的。但是采用此方法在求解协方差矩阵R的过程中,没有利用到杂波的先验信息。因此为了补偿训练数据的不足,本文为协方差矩阵R指定一个合适的先验分布。
文献[19-20]表明逆复Wishart分布是多维高斯分布中协方差矩阵的共轭先验分布。文献[21]通过对非均匀干扰杂波下协方差矩阵先验分布建模以及真实的雷达数据检测表明,逆复Wishart分布能反映实际的杂波信息。综合以上2点,本文采用逆复Wishart分布作为杂波协方差矩阵R的先验分布。为了模拟非均匀杂波环境,本文所采用的统计模型是文献[22]中随机协方差矩阵的扩展。即
| $ \boldsymbol{R}_{m n} \sim \mathcal{C} \mathcal{W}^{-1}\left(\mu, \boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{0}\right). $ | (2) |
其中:μ是自由度, λmn(μ-L)R0表示先验协方差矩阵结构。与之前的模型[20]相比,本文采用随机矩阵Rmn模拟不同发射-接收对所观测到的杂波信息。λmn表示不同Tx-Rx之间的功率水平,以此模拟非均匀杂波环境。R0是N×N维的正定矩阵。协方差矩阵Rmn的概率密度函数为
| $ \begin{gathered} f_{R}\left(\boldsymbol{R}_{m n} \mid \boldsymbol{\lambda}_{m n}\right)= \\ \frac{\left|\boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{0}\right|^{\mu}}{G(\mu, L)\left|\boldsymbol{R}_{m n}\right|^{\mu+L}} \exp \left\{-\operatorname{tr}\left[\boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{m n}^{-1} \boldsymbol{R}_{0}\right]\right\}, \end{gathered} $ | (3) |
| $ G(\mu, L)={\rm{ \mathsf{ π} }}^{L(L-1) / 2} \prod\nolimits_{l=1}^{L} \Gamma(u-l+1) . $ | (4) |
在实际应用中,矩阵R0代表杂波协方差矩阵的均值。可以通过地理信息系统、数字地形高程模型和综合脉冲孔径雷达SIAR成像等[3, 23]手段获取。逆复Wishart分布的自由度μ决定协方差矩阵结构R和R0的距离,μ越大表明R与R0之间的距离越小,即先验信息越可信。
2 基于贝叶斯的Rao检测器本节将推导出B-Rao检测器。假设Rmn和λmn已知的情况下,接收信号在假设H1和H0下的概率密度函数分别表示为
| $ \begin{gathered} f_{0}\left(\boldsymbol{X}_{m n} \mid \boldsymbol{\lambda}_{m n}, \boldsymbol{R}_{m n}\right)= \\ \frac{{\rm{ \mathsf{ π} }}^{-L H}}{\left|\boldsymbol{R}_{m n}\right|^{H}} \exp \left\{-\operatorname{tr}\left(\boldsymbol{X}_{m n} \boldsymbol{R}_{m n}^{-1} \boldsymbol{X}_{m n}^{\dagger}\right)\right\}, \end{gathered} $ | (5) |
| $ \begin{gathered} f_{1}\left(\boldsymbol{X}_{m n} \mid \boldsymbol{\alpha}_{m n}, \boldsymbol{\lambda}_{m n}, \boldsymbol{R}_{m n}\right)= \\ \frac{{\rm{ \mathsf{ π} }}^{-L H}}{\left|\boldsymbol{R}_{m n}\right|^{\mathrm{H}}} \exp \left\{-\operatorname{tr}\left(\boldsymbol{Y}_{m n} \boldsymbol{R}_{m n}^{-1} \boldsymbol{Y}_{m n}^{\dagger}\right)\right\}. \end{gathered} $ | (6) |
其中
| $ \boldsymbol{Y}_{m n}=\boldsymbol{X}_{m n}-\boldsymbol{\alpha}_{m n} \boldsymbol{p}_{\mathrm{r}, m n} \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m}. $ | (7) |
为了在推导过程中利用协方差矩阵Rmn的先验信息,拟采用2步法来推导B-Rao检测器。首先假设协方差矩阵Rmn是确定且已知的。在问题(1)中的相关参数可以表示为θr=αmn, θs=[λmn, ver(Rmn)]。θ=[θrT, θsT]T。
且Fisher信息矩阵如下
| $ \boldsymbol{I}(\boldsymbol{\theta})=\left[\begin{array}{ll} \boldsymbol{I}_{\mathrm{rr}}(\boldsymbol{\theta}) & \boldsymbol{I}_{\mathrm{rs}}(\boldsymbol{\theta}) \\ \boldsymbol{I}_{\mathrm{sr}}(\boldsymbol{\theta}) & \boldsymbol{I}_{\mathrm{ss}}(\boldsymbol{\theta}) \end{array}\right]. $ | (8) |
其中:
| $ \boldsymbol{I}_{x y}(\boldsymbol{\theta})=-E\left[\frac{\partial^{2}}{\partial \theta_{x}^{*} \partial \theta_{y}^{T}} \ln \left(f\left(x \mid \alpha, \boldsymbol{R}, H_{1}\right)\right)\right]. $ | (9) |
根据文献[24],Rao检测器可以表示为
| $ \left.\left.\frac{\partial \ln f_{1}(x)}{\partial \theta_{r}}\right|_{\theta=\theta_{0}} ^{T}\left\{\left[\boldsymbol{I}(\boldsymbol{\theta})^{-1}\right]_{\mathrm{rr}}\right\}_{\boldsymbol{\theta}=\theta_{0}} \frac{\partial \ln f_{1}(x)}{\partial \theta_{r}^{*}}\right|_{\boldsymbol{\theta}=\theta_{0}} \frac{>}{<} \eta. $ | (10) |
θ0是θ在假设H0下的最大似然估计,且
| $ \left[\boldsymbol{I}(\theta)^{-1}\right]_{\mathrm{rr}}=\left[\boldsymbol{I}_{\mathrm{rr}}(\theta)-\boldsymbol{I}_{\mathrm{rs}}(\theta) I_{\mathrm{ss}}^{-1}(\theta) \boldsymbol{I}_{\mathrm{sr}}(\theta)\right]^{-1}. $ | (11) |
对式(6)求对数,可知
| $ \begin{gathered} \ln f_{1}\left(\boldsymbol{X}_{m n} \mid \boldsymbol{\alpha}_{m n}, \boldsymbol{\lambda}_{m n}, \boldsymbol{R}_{m n}\right)= \\ -L H \ln {\rm{ \mathsf{ π} }}-H \ln \left|\boldsymbol{R}_{m n}\right|-\operatorname{tr}\left(\boldsymbol{Y}_{m n} \boldsymbol{R}_{m n}^{-1} \boldsymbol{Y}_{m n}^{\dagger}\right). \end{gathered} $ | (12) |
式(12)分别对αmn和αmn*求解导数, 并忽略无关常数项。
| $ \begin{gathered} \frac{\partial \ln f_{1}\left(\boldsymbol{X}_{m n} \mid \boldsymbol{\alpha}_{m n}, \boldsymbol{\lambda}_{m n}, \boldsymbol{R}_{m n}\right)}{\partial \boldsymbol{\alpha}_{m n}}= \\ \frac{\partial \operatorname{tr}\left(\boldsymbol{Y}_{m n} \boldsymbol{R}_{m n}^{-1} \boldsymbol{Y}_{m n}^{\dagger}\right)}{\partial \boldsymbol{\alpha}_{m n}}=\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{Y}_{m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n} . \end{gathered} $ | (13) |
| $ \begin{gathered} \frac{\partial \ln f_{1}\left(\boldsymbol{X}_{m n} \mid \boldsymbol{\alpha}_{m n}, \boldsymbol{\lambda}_{m n}, \boldsymbol{R}_{m n}\right)}{\partial \boldsymbol{\alpha}_{m n}^{*}}= \\ \frac{\partial \operatorname{tr}\left(\boldsymbol{Y}_{m n} \boldsymbol{R}_{m n}^{-1} \boldsymbol{Y}_{m n}^{\dagger}\right)}{\partial \boldsymbol{\alpha}_{m n}^{*}}=\boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{Y}_{m n} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} . \end{gathered} $ | (14) |
将式(13)代入式(9)中,并令αmn=0可得
| $ \boldsymbol{I}(\boldsymbol{\theta})_{\mathrm{rr}}=\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}. $ | (15) |
对式(13)求解关于vecT(Rmn*)的导数,然后对结果求期望
| $ \boldsymbol{I}(\boldsymbol{\theta})_{\mathrm{rs}}=0_{1 \times M N}. $ | (16) |
那么,式(11)可推导为
| $ [\boldsymbol{I}(\boldsymbol{\theta})]_{\mathrm{rr}}^{-1}=\left(\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m {n}} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}\right)^{-1} . $ | (17) |
将式(13)、式(14)和式(17)代入式(10)中并令αmn=0,可推导出当Rmn已知时的Rao检测器表达式为
| $ \prod\nolimits_{m, n} \frac{\left|\boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{X}_{m n} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n}\right|^{2}}{\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}} \frac{>}{<} \eta. $ | (18) |
为了推导出完整的B-Rao检测器,需求得Rmn在假设条件H0下的估计
| $ \begin{aligned} \hat{\boldsymbol{R}}_{m n} \mid \boldsymbol{\lambda}_{m n} &=\max \limits_{R}\left[f_{0}\left(\boldsymbol{X} \mid \boldsymbol{R}, \boldsymbol{\lambda}_{m n}\right) f_{R}\left(\boldsymbol{R} \mid \boldsymbol{\lambda}_{m n}\right)\right] \\ &=\max \limits_{R} \ln \left[f_{0}\left(\boldsymbol{X} \mid \boldsymbol{R}, \boldsymbol{\lambda}_{m n}\right) f_{R}\left(\boldsymbol{R} \mid \boldsymbol{\lambda}_{m n}\right)\right]. \end{aligned} $ | (19) |
代入式(3)、式(4)可知,关于Rmn的似然函数为
| $ \begin{gathered} \ln \left[f_{0}\left(\boldsymbol{X} \mid \boldsymbol{R}, \boldsymbol{\lambda}_{m n}\right) f_{R}\left(\boldsymbol{R} \mid \boldsymbol{\lambda}_{m n}\right)\right]= \\ -L H \ln {\rm{ \mathsf{ π} }}-H \ln \left|\boldsymbol{R}_{m n}\right|+\mu \ln \left|\boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{0}\right|- \\ \ln G(\mu, L)-(\mu+L) \ln \left(\left|\boldsymbol{R}_{m n}\right|\right)- \\ \operatorname{tr}\left(\boldsymbol{X}_{m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{X}_{m n}\right)-\operatorname{tr}\left(\boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{m n}^{-1} \boldsymbol{R}_{0}\right). \end{gathered} $ | (20) |
对式(20)求解关于Rmn的导数,并令其结果等于0。
| $ \begin{gathered} \boldsymbol{R}_{m n}^{-1} \boldsymbol{X}_{m n} \boldsymbol{X}_{m n}^{\dagger} \boldsymbol{R}_{m n}^{-1}+\boldsymbol{R}_{m n}^{-1} \boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{0} \boldsymbol{R}_{m n}^{-1}- \\ (H+\mu+L) \boldsymbol{R}_{m n}^{-1}=0. \end{gathered} $ | (21) |
则Rmn在假设H0下的估计为
| $ \hat{\boldsymbol{R}}_{m n} \mid \boldsymbol{\lambda}_{m n}=\frac{\boldsymbol{X}_{m n} \boldsymbol{X}_{m n}^{\dagger}+\boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{0}}{H+\mu+L} . $ | (22) |
式(22)是在假设λmn已知的情况下推导出的协方差矩阵估计量,但是实际λmn未知。因此也需要使用1个合适的估计量对其进行替换。根据文献[14]B4,可得λmn的MLE(maximum likelihood estimate)为
| $ \hat{\boldsymbol{\lambda}}_{m n}=\frac{\mu+1-L}{L} \boldsymbol{X}_{m n}^{\dagger}\left((\mu-L) \boldsymbol{R}_{0}\right)^{-1} \boldsymbol{X}_{m n}. $ | (23) |
利用推导出的
| $ \prod\nolimits_{m, n} \frac{\left|\boldsymbol{p}_{m n}^{\dagger}\left(\boldsymbol{X}_{m n} \boldsymbol{X}_{m n}^{\dagger}+\boldsymbol{X}_{m n}^{\dagger} \boldsymbol{R}_{0}^{-1} \boldsymbol{X}_{m n} \boldsymbol{R}_{0}\right) \boldsymbol{X}_{m n} \boldsymbol{p}_{\mathrm{t}, m n}\right|^{2}}{\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger}\left(\boldsymbol{X}_{m n} \boldsymbol{X}_{m n}^{\dagger}+\boldsymbol{X}_{m n}^{\dagger} \boldsymbol{R}_{0}^{-1} \boldsymbol{X}_{m n} \boldsymbol{R}_{0}\right) \boldsymbol{p}_{\mathrm{r}, m n}} \frac{>}{<} \eta_{1}. $ | (24) |
η1表示修改后的判决门限。
3 基于贝叶斯的Wald检测器本节将推导出B-Wald检测器。与B-Rao检测器推导过程类似,也采用2步法进行推导。首先假设Rmn和λmn都是确定且已知。根据文献[24],Wald检测器的判决公式为
| $ \left(\hat{\theta}_{r, 1}-\hat{\theta}_{r, 0}\right)^{\dagger}\left\{\left[\boldsymbol{I}\left(\theta_{1}\right)^{-1}\right]_{\mathrm{rr}}\right\}^{-1}\left(\theta_{r, 1}-\theta_{r, 0}\right) \frac{>}{<} \epsilon, $ | (25) |
其中:
代入Ymn†到式(13),并令其结果等于0可推导出
| $ \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m}\left(\boldsymbol{X}_{m n}-\boldsymbol{\alpha}_{m n} \boldsymbol{p}_{\mathrm{r}, m n} \boldsymbol{p}_{t, m n}^{\dagger} \boldsymbol{S}_{m}\right)^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}=0. $ | (26) |
进一步计算可知αmn在假设H1下的MLE估计为
| $ \hat{\boldsymbol{\alpha}}_{m n}=\frac{\boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{X}_{m n} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{r, m n}^{\dagger}}{\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m {n}} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}} . $ | (27) |
对式(17)求逆,可得
| $ \left\{\left[\boldsymbol{I}\left(\theta_{1}\right)^{-1}\right]_{\mathrm{rr}}\right\}^{-1}=\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}. $ | (28) |
代入式(27)、式(28)到式(25)中,可求得当Rmn已知时的Wald检测器表达式为
| $ \prod\nolimits_{m, n} \frac{\left|\boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m}^{-1} \boldsymbol{X}_{m n} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n}\right|^{2}}{\boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, {mn}}} \frac{>}{<} \epsilon. $ | (29) |
为了推导出完整的B-Wald检测器,与B-Rao检测器推导过程类似,需要推导出Rmn在假设H1下的估计
| $ \begin{aligned} \hat{\boldsymbol{R}}_{m n} \mid \boldsymbol{\lambda}_{m n} &=\max \limits_{R}\left[f_{1}\left(X \mid \boldsymbol{\alpha}_{m n}, \boldsymbol{R}, \boldsymbol{\lambda}_{m n}\right) f_{R}\left(\boldsymbol{R} \mid \boldsymbol{\lambda}_{m n}\right)\right] \\ &=\max \limits_{R} \ln \left[f_{1}\left(X \mid \boldsymbol{\alpha}_{m n}, \boldsymbol{R}, \boldsymbol{\lambda}_{m n}\right) f_{R}\left(\boldsymbol{R} \mid \boldsymbol{\lambda}_{m n}\right)\right], \end{aligned} $ | (30) |
代入式(3)、式(4)、式(6)和式(7),并对其求对数。
| $ \begin{gathered} \ln \left[f_{1}\left(X \mid \boldsymbol{\alpha}_{m n}, \boldsymbol{R}, \boldsymbol{\lambda}_{m n}\right) f_{R}\left(\boldsymbol{R} \mid \lambda_{m n}\right)\right]= \\ -L H \ln {\rm{ \mathsf{ π} }}-H \ln \left|\boldsymbol{R}_{m n}\right|+\mu \ln \left|\boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{0}\right|- \\ \operatorname{tr}\left(\boldsymbol{Y}_{m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{Y}_{m n}\right)-\operatorname{tr}\left(\boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{m n}^{-1} \boldsymbol{R}_{0}\right)- \\ \ln G(\mu, L)-(\mu+L) \ln \left(\left|\boldsymbol{R}_{m n}\right|\right). \end{gathered} $ | (31) |
对式(31)求关于Rmn的导数并令结果等于0,经变换可得
| $ \begin{gathered} (H+\mu+L) \boldsymbol{R}_{m n}=\boldsymbol{X}_{m n}^{\dagger} \boldsymbol{X}_{m n}+\boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{0}- \\ \frac{\boldsymbol{p}_{\mathrm{r}, m n} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{X}_{m n} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{X}_{m n}^{\dagger}}{\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}}+\\ \frac{\left|\boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{X} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n}\right|^{2} \boldsymbol{p}_{\mathrm{r}, m n} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger}}{\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n}\left(\boldsymbol{p}_{r, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}\right)^{2}}- \\ \frac{\boldsymbol{X}_{m n} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{X}_{m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger}}{\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}} . \end{gathered} $ | (32) |
式(32)左右两边同时乘以
| $ \begin{gathered} (H+\mu+L) \boldsymbol{p}_{\mathrm{r}, m n}=\boldsymbol{X}_{m n}^{\dagger} \boldsymbol{X}_{m n} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}+ \\ \boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{0} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}-\\ \frac{\boldsymbol{X}_{m n} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{X}_{m n}^{\dagger} \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}}{\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n}}= \\ \left(\boldsymbol{X}_{m n} \psi \boldsymbol{X}_{m n}^{\dagger}+\boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{0}\right) \boldsymbol{R}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n}. \end{gathered} $ | (33) |
最终可得Rmn在假设H1下的MAP估计为
| $ \hat{\boldsymbol{R}}_{m n}=\frac{\boldsymbol{X}_{m n} \psi \boldsymbol{X}_{m n}^{\dagger}+\boldsymbol{\lambda}_{m n}(\mu-L) \boldsymbol{R}_{0}}{H+\mu+L}. $ | (34) |
其中:
| $ \psi=I-\frac{\boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m}}{\boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{\mathrm{t}, m n}} . $ | (35) |
根据文献[14]B3,可得λmn在假设H1下的MLE估计为
| $ \hat{\boldsymbol{\lambda}}_{m n}=\frac{\mu+1-L}{L} \boldsymbol{Y}_{m n}^{\dagger}\left((\mu-L) \boldsymbol{R}_{0}\right)^{-1} \boldsymbol{Y}_{m n}. $ | (36) |
结合式(29)、式(34)、式(35)和式(36),忽略无关常数项,得到最终的B-Wald检测器为
| $ \prod\nolimits_{m, n} \frac{\left|\boldsymbol{p}_{\mathrm{r}, m n}^{\dagger}\left(\boldsymbol{X}_{\operatorname{mn}} \psi \boldsymbol{X}_{m n}^{\dagger}+\boldsymbol{Y}_{m n}^{\dagger} \boldsymbol{R}_{0}^{-1} \boldsymbol{Y}_{m n} \boldsymbol{R}_{0}\right) \boldsymbol{X}_{m n} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{t, m n}\right|^{2}}{\boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{S}_{m} \boldsymbol{S}_{m}^{\dagger} \boldsymbol{p}_{t, m} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger}\left(\boldsymbol{X}_{m n} \psi \boldsymbol{X}_{m n}^{\dagger}+\boldsymbol{Y}_{m n}^{\dagger} \boldsymbol{R}_{0}^{-1} \boldsymbol{Y}_{m n} \boldsymbol{R}_{0}\right) \boldsymbol{p}_{\mathrm{r}, {mn}}} \frac{>}{<} \epsilon_{1}. $ | (37) |
在本节中,通过仿真实验对比本文提出的检测器与传统的非贝叶斯检测器之间的检测性能。为了对比,这里给出文献[14]提出的KA-GLRT检测器
| $ \prod\nolimits_{m, n} \frac{\hat{\boldsymbol{\lambda}}_{m n, 0}^{\frac{u L}{\mu+H}}\left|\boldsymbol{X}_{m n} \boldsymbol{X}_{m n}^{\dagger}+\hat{\boldsymbol{\lambda}}_{m n, 0}(\mu-L) \boldsymbol{R}_{0}\right|}{\hat{\boldsymbol{\lambda}}_{m n, 1}^{\frac{u L}{\mu+H}}\left|\boldsymbol{Y}_{m n} \boldsymbol{Y}_{m n}^{\dagger}+\hat{\boldsymbol{\lambda}}_{m n, 1}(\mu-L) \boldsymbol{R}_{0}\right|} \frac{>}{<} \xi. $ | (38) |
对比本文提出的B-Rao和B-Wald检测器可知,因为KA-GLRT算法推导采用的是传统广义似然比检验的检测准则,其推导公式如下
| $ \frac{\max \limits_{\alpha, \lambda} \prod\nolimits_{m, n} \int f_{1}\left(\boldsymbol{X}_{m n} \mid \boldsymbol{\alpha}_{m n}, \boldsymbol{R}_{m n}\right) f\left(\boldsymbol{R}_{m n} \mid \boldsymbol{\lambda}_{m n}\right) \mathrm{d} \boldsymbol{R}_{m n}}{\max \limits_{\lambda} \prod\nolimits_{m, n} \int f_{0}\left(\boldsymbol{X}_{m n} \mid \boldsymbol{\alpha}_{m n}, \boldsymbol{R}_{m n}\right) f\left(\boldsymbol{R}_{m n} \mid \boldsymbol{\lambda}_{m n}\right) \mathrm{d} \boldsymbol{R}_{m n}} \frac{>}{<} \xi_{1}. $ | (39) |
在求解KA-GLRT时,需要做复杂的积分运算。而且需要同时求解假设H1和假设H0下关于αmn, h的似然函数和协方差矩阵Rmn的估计。而B-Rao和B-Wald在计算过程中不需要求积分,且只需要推导其中一个假设条件下的相关参数即可。在计算复杂度上B-Rao和B-Wald更低。
传统SCM检测器如下
| $ T_{\mathrm{scm}}=\prod\nolimits_{m, n} \sum\nolimits_{h=1}^{H} \frac{\left|\boldsymbol{x}_{m n, h}^{\dagger} \hat{\boldsymbol{R}}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n} \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger}\right|^{2}}{\boldsymbol{p}_{\mathrm{t}, m n} \boldsymbol{p}_{\mathrm{r}, m n}^{\dagger} \hat{\boldsymbol{R}}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n} \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger}} . $ | (40) |
其中:
| $ \hat{\boldsymbol{R}}_{m n}=\frac{1}{T} \sum\nolimits_{t=1}^{T} \boldsymbol{x}_{m n}^{(t)} \boldsymbol{x}_{m n}^{(t) \dagger}. $ | (41) |
RSCM检测器如下
| $ \begin{gathered} T_{\mathrm{rscm}}=\prod\nolimits_{m, n} \sum\nolimits_{h=1}^{H}(1-\\ \left.\frac{\left\|\boldsymbol{x}_{m n, h}^{\dagger} \hat{\boldsymbol{M}}_{m n}^{-1} \boldsymbol{p}_{r, m \boldsymbol{}} \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger}\right\|^{+}}{\boldsymbol{p}_{\mathrm{t}, m \boldsymbol{n}} \boldsymbol{\boldsymbol { p }}_{\mathrm{r}, m n}^{\dagger} \hat{\boldsymbol{M}}_{m n}^{-1} \boldsymbol{p}_{\mathrm{r}, m n} \boldsymbol{p}_{\mathrm{t}, m n}^{\dagger} \sum\nolimits_{h=1}^{H} \boldsymbol{x}_{m n, h}^{\dagger} \hat{\boldsymbol{M}}_{m n}^{-1} \boldsymbol{x}_{m n, h}}\right)^{-N}. \end{gathered} $ | (42) |
其中:
| $ \hat{\boldsymbol{M}}_{m n}^{-1}=\frac{L}{T} \sum\nolimits_{t=1}^{T} \frac{\boldsymbol{x}_{m n}^{(t)} \boldsymbol{x}_{m n}^{(t) \dagger}}{\boldsymbol{x}_{m n}^{(t) \dagger} \hat{\boldsymbol{M}}_{m n}^{-1} \boldsymbol{x}_{m n}^{(t)}}. $ | (43) |
因为推导出B-Wald检测器与B-Rao检测器的检测概率(probability of detection, PD)和虚警概率(probability of false alarm, PFA)的闭集表达式过于困难。本文采用蒙特卡罗仿真实验求解PD。在蒙特卡罗仿真实验中,PFA设为10-2,检测门限和检测概率通过100/PFA独立仿真实验求得。为了在相同的仿真环境下,比较KA-GLRT、SCM、RSCM检测器和本文推导的B-Rao、B-Wald检测器的检测性能,本文采用与文献[14]相同的仿真参数配置。
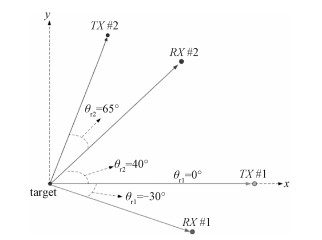
分布式MIMO雷达配置如图 1所示,发射天线阵元数和接收天线阵元数都为2。其中相对于目标0°和65°2个发射天线,相对于-30°和40°有2个接收天线。天线配置与文献[14]一致。为了模拟真实的雷达场景,假设发射脉冲重复频率为500 Hz,载波频率设为1 GHz,被测目标运动速度为108 km/h,由以上参数可得目标的归一化多普勒频率为0.2。假设发射脉冲数L=20,逆复Wishart分布的自由度μ=24以及λ11=1,λ12=2,λ21=3,λ22=4。为了简化运算,假设αmn, h在不同的距离单元内是相同的。R0采用指数相关的协方差矩阵,即第(m,n)个元素是
| $ \boldsymbol{R}_{0}(m, n)=\rho^{|m-n|}, $ | (44) |
|
Download:
|
| 图 1 分布式MIMO雷达配置图 Fig. 1 Distributed MIMO radar configuration | |
ρ=0.9表示1阶迟滞相关系数,信噪比(signal-to-noise ratio, SNR)定义为
| $ \mathrm{SNR}=L \sum\nolimits_{m n} \frac{\sum\nolimits_{h=1}^{H}\left|\alpha_{m n, h}\right|^{2}}{\lambda_{m n}}. $ | (45) |
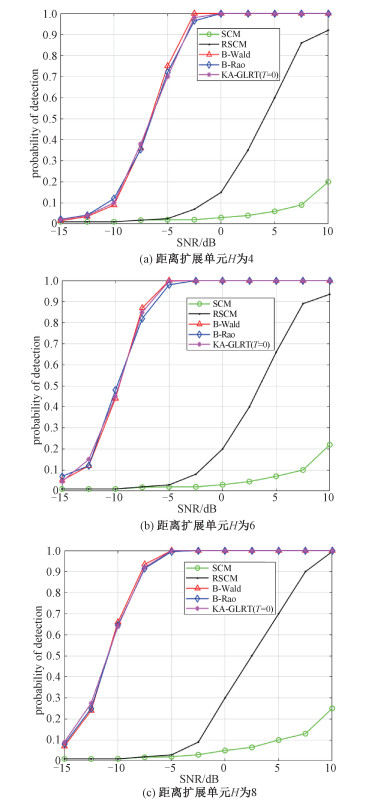
图 2(a)~2(c)分别对应着距离扩展单元H=4,H=6,H=8这3种情况下目标PD和SNR之间的关系曲线图。从图 2(a)可以看出:1)在相同SNR下,本文推导的B-Wald和B-Rao检测器的PD远高于现存的SCM检测器和RSCM检测器。这是因为B-Rao和B-Wald检测器在决策准则中包含杂波的先验信息,并以此实现了性能增益。2) 在相同SNR下,B-Wald和B-Rao检测器的PD与基于知识辅助的广义似然比(KA-GLRT) 检测器的PD相差不大。3) 图 2所有检测器的PD都随着SNR的增加而升高,且上升趋势相同。
|
Download:
|
| 图 2 不同距离扩展单元下,检测概率与SNR曲线图 Fig. 2 Probability of detection vs SNR diagram under different range cell | |
纵向比较图 2(a)~2(c)可知,随着距离扩展单元H的增大,各个检测器的检测性能都得到一定的提升。相较于传统的点源模型,目标回波扩展到多个距离单元。接收天线能收集到更多的回波信号,可以获得更多的目标信息,这在一定程度上提升了目标的检测概率。也从侧面印证了H越大,代表着雷达的距离分辨率越高,对目标的检测概率也相应更高。
由于本次蒙特卡罗仿真实验中设置M=N=2,发射阵元天线数和接收阵元天线数都比较小。但是在实际场景中,分布式MIMO雷达的发射阵元天线数和接收阵元天线数大于等于2甚至远远大于2。而且M个发射阵元天线和N个接收阵元天线可以组成MN个观测通道。此时接收端需要处理的数据以乘法增加。那么在M或者N比较大的雷达系统中,降低检测器的计算复杂度就显得尤为重要。
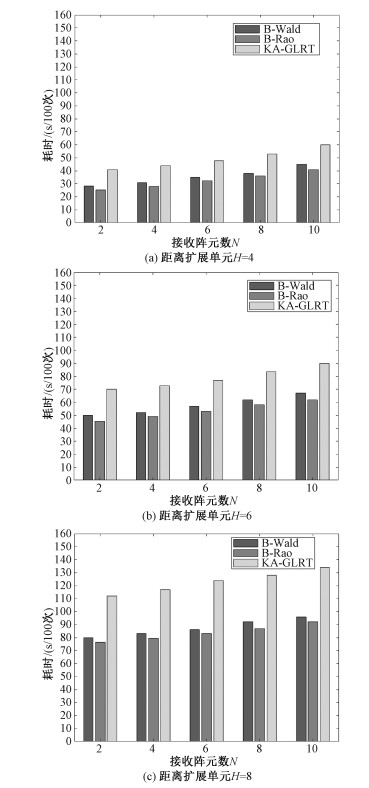
图 3(a)~3(c)分别表示在相同检测环境、不同的距离扩展单元下,B-Wald和B-Rao检测器与现存的KA-GLRT检测器的蒙特卡罗仿真实验耗时比较柱状图。由图 3(a)~3(c)可知,3种检测器的蒙特卡罗仿真耗时随着距离扩展单元H的增加而增大。这主要是因为距离扩展单元增大后,接收天线能收集到更多的回波信号,接收端需要处理的数据量更多。在相同距离单元H与相同接收阵元数N下,B-Wald和B-Rao检测器所花费的时间平均仅约为KA-GLRT检测器的68 %。这说明B-Rao和B-Wald检测器的计算复杂度低于KA-GLRT检测器。为了模拟大型分布式MIMO雷达系统,本文设置不同的N值仿真实现。N越大,代表雷达系统的阵元数越大。由图 3(a)可知,B-Rao、B-Wald、KA-GLRT检测器的计算耗时随着接收阵元数N的增加而增大,但是B-Rao与B-Wald检测器的耗时增量小于KA-GLRT检测器的耗时增量。当N=10(类比大型分布式MIMO雷达系统)时,B-Rao和B-Wald检测器的蒙特卡罗仿真耗时远远小于KA-GLRT检测器。这说明在大型的分布式MIMO雷达系统(很多阵元天线)中,B-Rao和B-Wald检测器能更快地计算出结果。
|
Download:
|
| 图 3 不同距离扩展单元下B-Rao、B-Wald、KA-GLRT蒙特卡罗仿真耗时比较 Fig. 3 Time comparison of B-Rao, B-Wald, KA-GLRT in Monte Carlo simulation under different range cell | |
本文主要研究分布式MIMO雷达对距离扩展目标的检测问题。首先介绍该检测问题的信号模型,并将其建模成一个二元假设检验问题。将不同发送-接收对(Tx-Rx)所对应的干扰杂波协方差矩阵建模为随机矩阵。同时指定它们的先验分布为逆复Wishart分布。然后在贝叶斯框架下结合传统的Rao和Wald检测准则推导出2个新的检测器:B-Rao和B-Wald检测器。新提出的2种检测器不需要训练数据,解决了均匀性训练数据不足的问题。最后通过仿真实验证明,在相同的检测环境下,与传统的SCM和RSCM检测器相比,B-Rao和B-Wald检测器由于在判决准则中加入了杂波的先验信息,检测性能优于SCM和RSCM。而与KA-GLRT检测器相比,3种检测器在相同SNR下,求得的PD相差很小。但是B-Wald与B-Rao平均花费的时间只有KA-GLRT的68 %,新推导出的2种检测器比KA-GLRT检测器具有更低的计算复杂度。进一步的实验仿真证明,在大型分布式MIMO雷达系统中,当接收天线或者发射天线数较多时,本文推导的B-Rao和B-Wald检测器的计算效率更高。
| [1] |
Liu W J, Wang Y L, Liu J, et al. Adaptive detection without training data in colocated MIMO radar[J]. IEEE Transaction on Aerospace and Electronic Systems, 2015, 51(3): 2469-2479. Doi:10.1109/TAES.2015.130754 |
| [2] |
Tang B, Zhang Y, Tang J. An efficient minorization maximization approach for MIMO radar waveform optimization via relative entropy[J]. IEEE Transactions on Signal Processing, 2018, 66(2): 400-411. Doi:10.1109/TSP.2017.2771726 |
| [3] |
韩金旺, 张子敬, 刘军, 等. 基于贝叶斯的高斯杂波背景下MIMO雷达自适应检测算法[J]. 雷达学报, 2019, 8(4): 501-509. |
| [4] |
王珽, 赵拥军, 胡涛. 机载MIMO雷达空时自适应处理技术研究进展[J]. 雷达学报, 2015, 4(2): 136-148. |
| [5] |
Bekkerman I, Tabrikian J. Target detection and localization using MIMO radars and sonars[J]. IEEE Transactions on Signal Processing, 2006, 54(10): 3873-3883. Doi:10.1109/TSP.2006.879267 |
| [6] |
Xu L Z, Li J, Stoica P. Target detection and parameter estimation for MIMO radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 927-939. Doi:10.1109/TAES.2008.4655353 |
| [7] |
程子扬, 何子述, 王智磊, 等. 分布式MIMO雷达目标检测性能分析[J]. 雷达学报, 2017, 6(1): 81-89. |
| [8] |
He Q, Blum R S, Haimovich A M. Noncoherent MIMO radar for location and velocity estimation: more antennas means better performance[J]. IEEE Transactions on Signal Processing, 2010, 58(7): 3661-3680. Doi:10.1109/TSP.2010.2044613 |
| [9] |
He Q, Lehmann N H, Blum R S, et al. MIMO radar moving target detection in homogeneous clutter[J]. IEEE Transactions Aerospace and Electron Systems, 2010, 46(3): 1290-1301. Doi:10.1109/TAES.2010.5545189 |
| [10] |
Haimovich A M, Blum R S, Cimini L J. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116-129. Doi:10.1109/MSP.2008.4408448 |
| [11] |
Chong C Y, Pascal F, Ovarlez J P, et al. MIMO radar detection in non-Gaussian and heterogeneous clutter[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1): 115-126. Doi:10.1109/JSTSP.2009.2038980 |
| [12] |
Liu J, Liu W J, Han J W, et al. Persymmetric GLRT detection in MIMO radar[J]. IEEE Transactions on Vehicular Technology, 2018, 67(12): 11913-11923. Doi:10.1109/TVT.2018.2877265 |
| [13] |
Li H B, Wang Z, Liu J, et al. Moving target detection in distributed MIMO radar on moving platforms[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1524-1535. Doi:10.1109/JSTSP.2015.2467355 |
| [14] |
Gao Y C, Li H B, Himed B. Knowledge-aided ranged-spread target detection for distributed MIMO radar in nonhomogeneous environments[J]. IEEE Transactions on Signal processing, 2017, 65(3): 617-627. Doi:10.1109/TSP.2016.2625266 |
| [15] |
Liu J, Zhang Z J, Cao Y H, et al. A closed-form expression for false alarm rate of adaptive MIMO-GLRT detector with distributed MIMO radar[J]. Signal Processing, 2013, 93(9): 2771-2776. Doi:10.1016/j.sigpro.2013.03.001 |
| [16] |
De Maio A, Orlando D. Adaptive radar detection of a subspace signal embedded in subspace structured plus Gaussian interference via invariance[J]. IEEE Transactions on Signal Processing, 2016, 64(8): 2156-2167. Doi:10.1109/TSP.2015.2507544 |
| [17] |
王楠, 孙进平, 王文光. 非均匀环境下基于知识辅助的扩展目标Wald检测器[J]. 信号处理, 2018, 34(6): 714-721. |
| [18] |
Liu J, Zhang Z J, Cao Y H, et al. Distributed target detection in subspace interference plus Gaussian noise[J]. Signal Processing, 2014, 95: 88-100. Doi:10.1016/j.sigpro.2013.08.012 |
| [19] |
Bouriga M, Féron O. Estimation of covariance matrix based on hierarchical inverse-Wishart priors[J]. Journal of Statistical Planning and Inference, 2013, 143(4): 795-808. Doi:10.1016/j.jspi.2012.09.006 |
| [20] |
Steven W, Nydick. The Wishart and inverse Wishart distributions[EB/OL]. (2012-05-23)[2019-11-13]. https://pdfs.semanticscholar.org/ac51/ee74af59c432d493da98bd950cc6f856a0ca.pdf.
|
| [21] |
De Maio A, Farina A, Foglia G. Knowledge-aided Bayesian radar detectors & their application to live data[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 170-183. Doi:10.1109/TAES.2010.5417154 |
| [22] |
Conte E, De Maio A, Ricci G. Recursive estimation of the covariance matrix of a compound-Gaussian process and its application to adaptive CFAR detection[J]. IEEE Transactions on Signal Processing, 2002, 50(8): 1908-1915. Doi:10.1109/TSP.2002.800412 |
| [23] |
马肖肖, 程博, 刘岳明, 等. 基于极化特征和纹理特征的PolSAR影像建筑物提取方法[J]. 中国科学院大学学报, 2019, 36(5): 682-693. |
| [24] |
Liu W J, Wang Y L, Xie W C. Fisher information matrix, Rao test, and Wald test for complex-valued signals and their applications[J]. Signal Processing, 2014, 94(1): 1-5. |
| [25] |
Bandiera F, Besson O, Coluccia A, et al. ABORT-like detectors: a Bayesian approach[J]. IEEE Transactions on Signal Processing, 2015, 63(19): 5274-5284. Doi:10.1109/TSP.2015.2451117 |
 2021, Vol. 38
2021, Vol. 38 


