2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
高分三号遥感卫星是中国第一颗分辨率达到1 m的C频段多极化SAR卫星,共有12种成像模式,可满足多种不同的应用需求。高分三号可全天时、全天候地监测全球海洋和陆地资源,是高分专项工程实现对地观测目标的重要基础[1]。高分三号卫星分辨率高、观测范围广、成像模式多,使得立体SAR图像对的获取变得更加便捷高效,这为立体SAR图像定位方法的研究提供了极大的便利,在地形图测绘和地表形变监测等多方面有着广泛的应用前景。
立体SAR图像定位是根据SAR图像构像模型,由构成立体的两幅SAR图像的同名点坐标计算相应地面点三维坐标的过程[2-4]。立体SAR图像定位技术可以反演地物目标的三维信息,获取高程数据。
近年来,国内对于基于斜距多普勒模型[5]的立体定位方法研究甚少,大多是基于通用构像模型的立体定位研究[6-7];而国际上对于SAR图像立体定位技术的研究发展迅速,尤其是德国的TerraSAR-X,利用不同成像时间获得的立体像对根据斜距多普勒模型进行立体定位的精度已达米级水平,经过精细化处理后可达分米量级[8-9]。对比于目前极具潜力的干涉SAR技术[10-12],立体定位技术是根据不同成像位置获取相同地物信息时的视差值获取高程值[13],不受相干性的限制,理论上来说,即便立体像对间存在一定的成像时间间隔与轨道差异,其立体定位结果应几乎不会受到影响。因此,SAR图像立体定位方法相对来说成本较低、效率较高,且具有较高的实用价值。所以研究如何根据立体定位获得高精度的目标点三维信息具有十分重要的意义。
构建定位模型、卫星状态矢量的解算及定位方程组的解算是立体SAR图像定位的3个关键环节。斜距多普勒模型是一种基于SAR成像原理的定位模型,物理意义明确,在已知星历参数和传感器参数的基础上,利用该模型可以得到精度较高的目标点三维信息。本文首先根据斜距多普勒模型构建立体定位方程组,并利用卫星辅助数据以多项式拟合法拟合曲线,解算卫星天线相位中心的瞬时状态矢量。由于牛顿法具有较为固定的公式,且具有局部收敛性和较高的收敛阶[14],运算效率高,应用方便,因此本文利用牛顿法求解立体定位方程组。最后结合成像时间多样的高分三号SAR图像对进行多组立体定位实验,实验结果证明,选取SAR立体图像对的限制性更小,具有很高的任意性,获取方便,即便在立体像对轨道差别较大、成像时间间隔长达100 d时,仍然得到了精度较高的目标点三维信息,可靠性较高。
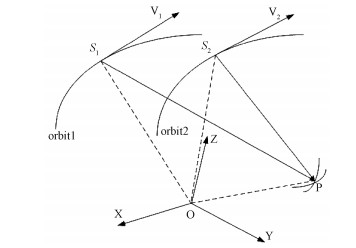
1 SAR图像立体定位原理SAR图像的立体定位原理可以描述为:雷达以2个不同的侧视角观测地面同一目标,获得包含该目标的2幅SAR图像,以人眼类比,此时可以产生立体感。因此,将这2幅SAR图像构成立体像对,根据相应的构像模型可以求解出地面目标点的三维坐标。示意图如图 1所示。
|
Download:
|
| 图 1 立体定位原理 Fig. 1 Principle of stereo positioning | |
斜距多普勒模型是一种符合SAR成像原理的严密模型,具有明确的物理意义,其包括1个距离条件方程和1个多普勒频移条件方程[6],其中距离条件方程表示为
| $ R=\left|\boldsymbol{R}_{s}-\boldsymbol{R}_{t}\right|, $ | (1) |
其中:R表示卫星天线相位中心的瞬时位置到地面目标点的斜距值,Rs表示卫星天线相位中心的瞬时位置矢量,
多普勒频移条件方程表示为
| $ f_{d c}=-\frac{2}{\lambda R}\left(\boldsymbol{R}_\boldsymbol{s}-\boldsymbol{R}_\boldsymbol{t}\right)\left(\boldsymbol{V}_\boldsymbol{s}-\boldsymbol{V}_\boldsymbol{t}\right), $ | (2) |
其中:fdc表示多普勒频移,λ表示波长,Vs表示卫星天线相位中心速度矢量,Vs=[Vx,Vy,Vz]T,Vt表示地面点目标速度矢量,Vt=[Vxt,Vyt,Vzt]T。
单幅SAR图像的斜距多普勒模型反映的是地面点三维坐标到SAR图像平面坐标的关系,是一个三维到二维的过程[15]。如果对地面同一目标点还存在着另一幅SAR图像,就可以得到另一组不同的斜距多普勒方程,即增加一个三维到二维的过程,此时对同一目标点一共存在2个距离条件方程和2个多普勒频移条件方程。
在地固坐标系下,地面点目标速度为0,此时立体定位方程组表示为
| $ \left\{\begin{array}{c} R_{1}=\left|\boldsymbol{R}_{\boldsymbol{s} 1}-\boldsymbol{R}_\boldsymbol{t}\right|, \\ R_{2}=\left|\boldsymbol{R}_{\boldsymbol{s} 2}-\boldsymbol{R}_\boldsymbol{t}\right|, \\ f_{d c 1}=-\frac{2}{\lambda R_{1}}\left(\boldsymbol{R}_{\boldsymbol{s} 1}-\boldsymbol{R}_\boldsymbol{t}\right) \boldsymbol{V}_{\boldsymbol{s} 1} ,\\ f_{d c 2}=-\frac{2}{\lambda R_{2}}\left(\boldsymbol{R}_{\boldsymbol{s} 2}-\boldsymbol{R}_\boldsymbol{t}\right) \boldsymbol{V}_{\boldsymbol{s} 2}. \end{array}\right. $ | (3) |
其中:Ri(i=1, 2)表示不同卫星天线相位中心的瞬时位置到地面目标点的距离矢量,Rsi表示不同卫星天线相位中心的瞬时位置矢量,Rsi=[Xsi,Ysi,Zsi]T(i=1, 2),Vsi表示不同SAR天线相位中心速度矢量,Vsi=[Vxi,Vyi,Vzi]T(i=1, 2),fdci(i=1, 2)表示多普勒频移。其余符号含义与上文相同。
2 求解立体定位方程组 2.1 卫星状态矢量的求解卫星辅助数据提供一定数量包含该图像范围的卫星状态矢量,为了能够获取任意时刻的卫星天线相位中心状态矢量,可以用多项式拟合得到状态矢量随时间变化的曲线方程。多个研究表明,当轨道参数精度较高时,多项式拟合法得到的值能达到很好的精度[16-17],其中使用6次多项式拟合位置矢量,表示为
| $ \left\{\begin{array}{l} X_{s}=a_{0}+a_{1} t+a_{2} t^{2}+a_{3} t^{3}+a_{4} t^{4}+a_{5} t^{5}+a_{6} t^{6}, \\ Y_{s}=b_{0}+b_{1} t+b_{2} t^{2}+b_{3} t^{3}+b_{4} t^{4}+b_{5} t^{5}+b_{6} t^{6}, \\ Z_{s}=c_{0}+c_{1} t+c_{2} t^{2}+c_{3} t^{3}+c_{4} t^{4}+c_{5} t^{5}+c_{6} t^{6}. \end{array}\right. $ | (4) |
其中:Xs、Ys、Zs表示卫星天线相位中心t时刻的位置,a0、a1,…,c0, c1, …,c6表示坐标拟合参数,t表示扫描时间。
使用3次多项式拟合速度矢量,表示为
| $ \left\{\begin{array}{l} V_{x}=a_{0}+a_{1} t+a_{2} t^{2}+a_{3} t^{3}, \\ V_{y}=b_{0}+b_{1} t+b_{2} t^{2}+b_{3} t^{3}, \\ V_{z}=c_{0}+c_{1} t+c_{2} t^{2}+c_{3} t^{3}. \end{array}\right. $ | (5) |
其中:Vx、Vy、Vz表示卫星天线相位中心t时刻的瞬时速度,其余数学符号含义同上文一致。
2.2 牛顿法求解立体定位方程组立体定位方程组是一个非线性方程组,形式复杂,当满足牛顿法收敛性时,使用牛顿法可以快速高效地进行求解。
利用矩阵的形式将该方程组表示为
| $ \boldsymbol{f}=\left[\begin{array}{l} \boldsymbol{f}_{1}(x, y, z) \\ \boldsymbol{f}_{2}(x, y, z) \\ \boldsymbol{f}_{3}(x, y, z) \\ \boldsymbol{f}_{4}(x, y, z) \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \end{array}\right]. $ | (6) |
在[x(0), y(0), z(0)]T处进行Taylor级数展开,取线性项并整理得牛顿法公式为
| $ \begin{array}{c} &{\left[\begin{array}{l} x_{(k+1)} \\ y_{(k+1)} \\ z_{(k+1)} \end{array}\right]=\left[\begin{array}{l} x_{(k)} \\ y_{(k)} \\ z_{(k)} \end{array}\right]-\left[\boldsymbol{f}^{\prime}\left(x_{(k)}\right)\right]^{-1} \times} \\ &{\left[\begin{array}{l} \boldsymbol{f}_{1}\left(x_{(k)}, y_{(k)}, z_{(k)}\right) \\ \boldsymbol{f}_{2}\left(x_{(k)}, y_{(k)}, z_{(k)}\right) \\ \boldsymbol{f}_{3}\left(x_{(k)}, y_{(k)}, z_{(k)}\right) \\ \boldsymbol{f}_{4}\left(x_{(k)}, y_{(k)}, z_{(k)}\right) \end{array}\right] .} \end{array} $ | (7) |
如果初始值不足够靠近准确解,那么牛顿法将收敛得很慢,或者根本不收敛。为避免这种情况,本文首先将待测目标点高程设为0对其进行单景图像定位,并将此定位结果作为对该点进行立体定位时的初始值。
迭代阈值设置为ε=0.001 m,迭代的判停标准为
| $ \left|x_{k+1}-x_{k}\right| \leqslant \varepsilon. $ | (8) |
当满足式(8)时则可停止迭代,输出当前求出的解,即得到目标点三维坐标。
3 实验 3.1 数据来源本文利用高分三号在3种不同成像模式下得到的7景SAR图像进行实验,实验环境是MATLAB R2014a。
为了能够获得较多特征明显的目标点进行测试,本文选择重叠区域在60 % 以上的2景影像为1组立体像对进行实验。其中,1、2、3这3景两两组合进行3组实验,4和5为1组实验,6和7为1组实验,5组立体像对信息如下表 1所示。
|
|
表 1 5组立体图像对 Table 1 Five groups of SAR image pairs |
各景影像的基本信息如表 2所示。
|
|
表 2 影像基本信息 Table 2 Information of the images |
每组均通过手工选取5个特征明显的地面目标点进行实验。待测目标点在Google Earth上的分布如图 2所示。

|
Download:
|
| 图 2 待测目标点在Google Earth上的分布 Fig. 2 Positions of the targets on Google Earth | |
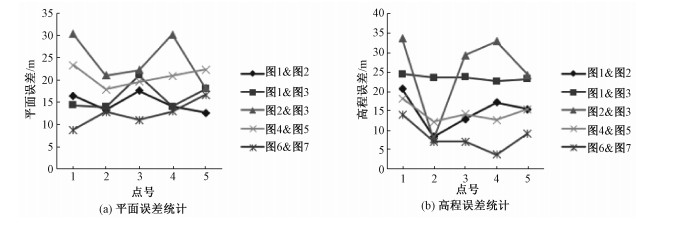
本文利用7景SAR图像得到5组实验结果,每组实验均手动选取5组特征明显的同名点,包括房屋一角、路口中心及广场一角等。将实验计算得到的三维信息与Google Earth上读取的位置坐标进行比较,得到平面误差和高程误差如图 3所示。
|
Download:
|
| 图 3 立体定位误差 Fig. 3 Stereo positioning errors | |
将所有立体像对定位得到的平均平面误差和平均高程误差统计见表 3。
|
|
表 3 立体定位平均误差统计 Table 3 Average errors of stereo positioning |
分析实验结果得到如下结论:
1) 从图 3可看出,利用本文立体定位方法得到的所有点的平面误差均不超过30 m,大多数点的平面误差集中在25 m内,高程误差均不超过34 m,多数集中在25 m内;
2) 分析第3组实验,即使立体像对的时间间隔长达100 d,其平面精度和高程精度最大值也都在35 m内,可靠性较高;
3) 比较表 3数据可以看出,虽然成像时间间隔最短的第5组实验定位误差最小、间隔最长的第3组实验定位误差最大,但是对比第1组和第4组结果来看,成像时间间隔短的立体像对定位误差反而更大一些,以上说明误差变化和立体像对的成像时间间隔并不相关,而出现以上结果的原因可能是手动选点时受到图像分辨率的影响,导致选点不够准确;
4) 基于以上结论进一步分析可知,3种成像模式中滑动聚束模式得到的立体像对定位精度最高,平面误差在17 m内,高程误差在14 m内。其中第1组同名点平面误差在10 m内,有4组同名点高程误差在10 m内,其中第4组同名点高程误差在5 m内。
4 结语本文介绍了一种定位精度较高的高分三号SAR图像立体定位方法。首先根据斜距多普勒模型建立立体定位方程组;求解卫星状态矢量时,分别利用6次多项式拟合法和3次多项式拟合法求解两卫星天线相位中心的瞬时位置矢量和速度矢量;最后利用牛顿法求解立体定位方程组,得到目标点的三维信息。
本文利用在3种不同成像模式下得到的7景SAR图像组成5组立体图像对进行立体定位实验,其成像时间间隔均在一周以上,最大时间间隔达100 d,均得到了精度较高的目标点三维信息,且在此基础上进一步分析可知,在滑动聚束模式下得到的立体像对定位精度最高。
| [1] |
丁赤飚, 刘佳音, 雷斌, 等. 高分三号SAR卫星系统级几何定位精度初探[J]. 雷达学报, 2017, 6(1): 11-16. |
| [2] |
张红敏. SAR图像高精度定位技术研究[D]. 郑州: 解放军信息工程大学, 2013.
|
| [3] |
Chen P H, Dowman I J. Space intersection from ers-1 synthetic aperture radar images[J]. The Photogrammetric Record, 1996, 15(88): 561-573. Doi:10.1111/0031-868X.00064 |
| [4] |
Eldhuset K, Weydahl D J. Geolocation and stereo height estimation using TerraSAR-X spotlight image data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3574-3581. Doi:10.1109/TGRS.2011.2160951 |
| [5] |
Curlander J C. Location of spaceborne SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 1982, GE-20(3): 359-364. Doi:10.1109/TGRS.1982.350455 |
| [6] |
Wang M, Wang Y L, Run Y, et al. Geometric accuracy analysis for GaoFen3 stereo pair orientation[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(1): 92-96. Doi:10.1109/LGRS.2017.2775204 |
| [7] |
Zhang G, Wu Q W, Wang T Y, et al. Block adjustment without GCPs for Chinese spaceborne SAR GF-3 imagery[J]. Sensors, 2018, 18(11): 4023. Doi:10.3390/s18114023 |
| [8] |
Balss U, Gisinger C, Eineder M. Measurements on the absolute 2-D and 3-D localization accuracy of TerraSAR-X[J]. Remote Sensing, 2018, 10(4): 656. Doi:10.3390/rs10040656 |
| [9] |
Gisinger C, Balss U, Pail R, et al. Precise three-dimensional stereo localization of corner reflectors and persistent scatterers with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 1782-1802. Doi:10.1109/TGRS.2014.2348859 |
| [10] |
马素颜. 基于高分辨率卫星遥感数据提取DEM方法研究[D]. 上海: 华东师范大学, 2009.
|
| [11] |
Sansosti E. A simple and exact solution for the interferometric and stereo SAR geolocation problem[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(8): 1625-1634. Doi:10.1109/TGRS.2004.831442 |
| [12] |
王琴, 陈蜜, 刘书军, 等. 利用升降轨道SAR数据获取DEM的试验研究[J]. 测绘通报, 2015(6): 39-43. |
| [13] |
荆创利. 使用SAR影像生成DEM的方法研究与精度分析[D]. 成都: 西南交通大学, 2008.
|
| [14] |
喻文健. 数值分析与算法[M]. 2版. 北京: 清华大学出版社, 2015.
|
| [15] |
尤红建, 付琨. SAR图像精准处理[M]. 北京: 科学出版社, 2010: 188-189.
|
| [16] |
袁修孝, 曹金山. 高分辨率卫星遥感精确对地目标定位理论与方法[M]. 北京: 科学出版社, 2012.
|
| [17] |
陈尔学. 星载合成孔径雷达影像正射校正方法研究[D]. 北京: 中国林业科学研究院, 2004.
|
 2021, Vol. 38
2021, Vol. 38 


