改革开放以来,中国工业化和城市化进程快速推进,经济持续高速增长并取得举世瞩目的辉煌成就。但粗放的经济发展模式使得经济总量增长的同时消耗大量资源、造成严重的环境污染,导致地区资源环境承载力下降。2014年以来,中国经济进入转型发展的“新常态”时期,经济发展不再只追求经济总量的上升,而是着眼于转变经济增长方式,提升经济发展质量,提高地区生态效率,以实现经济、生态和社会的综合可持续发展。
生态效率最初是1990年由Schaltegger和Sturm提出的,即增加的价值与增加的环境影响的比值[1]。世界可持续发展工商理事会认为,生态效率通过提供具有竞争力的商品与服务,在满足人类基本生活需求的同时,将生命周期中对环境的影响降到地球可承载的范围内[2]。生态效率的核心理念是用最少的资源消耗和最低的环境代价获取最大的经济效益。1995年,Fussler将生态效率引入中国[3],自此学者们对生态效率开展了大量富有成效的研究工作,可以概括为以下3个方面:一是对不同区域尺度、地区及城市[4-12]和不同行业[13-17]的研究,其中区域、地区层级的研究较多,而地级层面和县级层面的生态效率研究较少,因此生态效率的小尺度研究有待进一步完善。任宇飞等[18]利用传统和含有非期望产出的SBM模型(slack-based model)分析东部沿海四大城市群生态效率的时空特征及其影响因素。王敏和张晓平[19]利用主成分分析法和DEA(data envelopment analysis)相结合的方法对中国30个省市区的生态效率进行评价。郑德凤等[13]利用含有非期望产出的SBM模型测算甘肃省的农业生态效率。二是研究方法各异且日益拓展。主要有比值法[20-21]、指标体系法[22]、DEA法[23-26]等。比值法主要通过经济产出与资源消耗的比值计算生态效率;指标体系法主要针对不同的研究对象制定评价指标体系来计算生态效率;DEA法运用运筹学的思路,通过线性规划评价决策单元投入与产出之间的关系,测度相对有效程度。其中基于DEA及其扩展模型的研究方法可以有效避免主观设置权重,能够客观地测度城市的生态效率,因而应用广泛[27]。国内学者主要运用数据包络分析模型研究生态效率的时空格局演变特征,如方创琳和关兴良[28]利用传统DEA模型和Bootstrap-DEA方法测算中国城市群的投入产出效率,从时间和空间两个角度分析城市群投入产出效率的演变特征。王恩旭和武春友[29]利用超效率DEA模型计算1995—2007年中国省区的生态效率,并分析30个省区生态效率的时空演变特征。李青松等[30]运用SE-DEA模型和Malmquist指数模型计算2007—2012年河南省地级市的生态效率,分析生态效率的静态和动态变化趋势。三是在生态效率的影响因素研究方面,学者们结合不同的案例地区,主要从经济发展水平、经济外向度、产业结构、科技创新水平、环境规制、地区开放水平和城市化水平等方面,研究生态效率的影响因素[31-36]。但结合大样本、长时间序列的研究还有进一步深化的空间。综合学术界已有的研究,以地级市为空间单元进行较长时间尺度的对比和分析仍有待深化。
因此,本文以全国285个地级以上城市为研究对象,基于2005—2017年的面板数据,运用含有非期望产出的超效率SBM模型研究中国城市生态效率的时空演变特征,并运用面板回归模型探析中国城市生态效率的影响因素。
1 数据处理及研究方法 1.1 数据来源及指标选取考虑到近年来中国城市行政区划的变动情况和某些城市的数据缺失较多,本文以全国285个地级以上城市(不包括港澳台地区)为研究对象(以下简称为城市)。研究时段为2005—2017年,相关数据来源于《中国城市统计年鉴》、《新中国六十年统计资料汇编》、《中国统计年鉴》。
本文根据世界可持续发展工商理事会提出的生态效率的评价标准,参考其他学者的研究,并结合数据的可得性,构建生态效率的评价指标体系(表 1)。研究中,投入指标包括资本投入、劳动力投入、土地投入、能源投入和水资源投入,产出指标包括以经济收益为代表的期望产出和以污染物排放为代表的非期望产出。
|
|
表 1 中国城市生态效率评价指标体系 Table 1 Index for evaluation of urban eco-efficiency in China |
超效率Undesirable-SBM模型是数据包络分析DEA研究方法的拓展模型。DEA是一种不需要函数关系的非参数技术效率分析方法,它以多投入和多产出为基础,对决策单元进行相对有效性的评价。
传统的DEA模型有CCR模型和BCC模型,且在区域、经济、产业和企业等方面应用广泛。Tone[27]提出的SBM模型属于非径向、非角度的DEA模型,它在传统的径向、角度DEA模型基础上,将松弛变量(slack)纳入模型,能更有效地对决策单元进行效率评价;Tone[37]进一步提出超效率SBM模型,弥补了不能将同时有效的多个决策单元区分开来的问题。近年来,人们越来越关注环境质量,评价城市生态效率,必然要将污染物排放考虑进来,因此在现有模型的基础上将非期望产出纳入模型[38],从而更加有效地测算城市的真实生态效率。模型如下:
| $ \min \rho=\frac{1+\frac{1}{m} \sum_{i=1}^{m} s_{i}^{-} / x_{i k}}{1-\frac{1}{s} \sum_{r=1}^{s} s_{r}^{+} / y_{r k}}; $ | (1) |
| $ \text { s.t. } \sum_{j=1, j \neq k}^{n} x_{i j} \lambda_{j}-s_{i}^{-} \leqslant x_{i k}; $ | (2) |
| $ \sum_{j=1, j \neq k}^{n} y_{r j} \lambda_{j}+s_{r}^{+} \geqslant y_{r k}; $ | (3) |
| $ \left\{\begin{array}{c} \lambda, s^{-}, s^{+} \geqslant 0, \\ i=1, 2, \cdots, m \\ r=1, 2, \cdots, q, \\ j=1, 2, \cdots, n(j \neq k) . \end{array}\right. $ | (4) |
ρ为模型计算出来的城市生态效率,当ρ>1或者当ρ=1且s+=s-=0时,该城市的生态效率达到强有效状态;当ρ=1,s+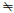
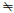
| $ \rho=P T E \times S E. $ | (5) |
本文基于上述模型和表 1的生态效率评价指标体系,运用MaxDEA7.0软件进行运算,以多投入和多产出模型为基础并设定非期望产出,计算样本城市相应的生态效率。基于ARCGIS空间分析模块对城市生态效率的空间格局进行分析。下文用TE(total efficiency)代表城市生态效率ρ。生态效率相关概念涵义如表 2所示。
|
|
表 2 生态效率及相关概念解释 Table 2 Definition of eco-efficiency and related concepts |
Spearman等级相关系数又称Spearman秩相关系数,是衡量2个变量间强弱关系的非参数检验方法。可以用单调函数来描述变量之间的相关性,若一个变量随另一个变量单调递增,Spearman秩相关系数为正,反之为负,Spearman秩相关系数取值范围为[-1, 1]。计算公式为
| $ r=1-\frac{6 \sum_{i=1}^{n} d_{i}^{2}}{n\left(n^{2}-1\right)}, $ | (6) |
式中:r表示等级相关系数,n为时间序列的长度,di为秩次之差。r的绝对值越接近于1,则单调递增(或递减)程度越高。本文利用SPSS计算2005—2017年的各城市生态效率的Spearman等级相关系数。
1.2.3 面板回归模型在对城市生态效率影响因素进行分析时,采用面板数据回归模型进行验证。回归模型公式如下
| $ Y_{i t}=\alpha_{i}+\sum_{k=1}^{k} \beta_{k i} X_{k i t}+u_{i t}, $ | (7) |
其中:i=1,2,3…N表示N个城市;t=1,2,3…T表示T个时期;Yit为被解释变量,表示t年份第i个城市的生态效率;Xkit为解释变量,表示在t时期第i个城市的第k个解释变量的值;βki为待估系数,uit为随机干扰项。
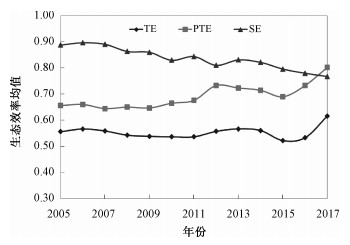
2 结果分析 2.1 中国城市生态效率的时间演变特征利用上述方法,对中国285个地级以上城市2005—2017年的城市生态效率进行测度,汇总结果如图 1所示。中国城市生态效率总体均值在2005—2014年间波动较小,在2014—2017年间呈现先下降后上升的趋势。总体来说,在研究期间生态效率呈现上升状态。纯技术生态效率在2005—2017年间呈现上升趋势,说明城市的资源配置及政府管理水平逐渐提升,对于生态效率的提升有促进作用。规模效率在2005—2017年间呈现逐渐下降的趋势,说明规模效率对城市生态效率的提升起着负向作用,规模扩张带来的增值效益日益减小。
|
Download:
|
| 图 1 2005—2017年全国城市生态效率均值变化趋势 Fig. 1 Trend of average urban eco-efficiency in China from 2005 to 2017 | |
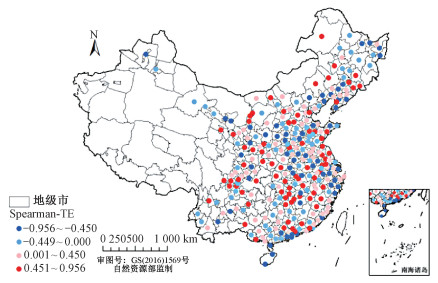
基于城市生态效率,计算2005—2017年285个城市的Spearman等级相关系数,并利用ArcGIS进行可视化(图 2)。由图 2可以看出,生态效率上升较快的城市主要分布在吉林、河北、陕西、湖北、湖南、江西、四川等中、西部省区,而沿海地区仅江苏、山东、广东等省的城市的生态效率上升较快。生态效率下降较快的城市主要分布在黑龙江、辽宁、山西、安徽、甘肃、山东等省区,浙江和广东等省的部分城市也位列其中。
|
Download:
|
| 图 2 2005—2017年城市生态效率的Spearman等级相关系数 Fig. 2 Spearman rank correlation coefficients of urban eco-efficiency from 2005 to 2017 | |
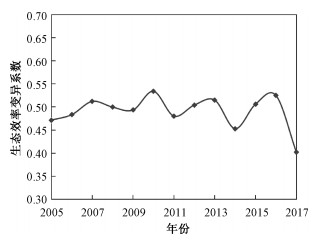
城市间生态效率的时间变化分析表明,中国城市的生态效率总体提升且城市间的差异减小。由于原来生态效率较低的城市在研究期内的生态效率水平不断提升,因此,缩小了与生态效率水平较高的城市间的差距。图 3是2005—2017年城市生态效率在全国总体的变异系数,略有波动,但总体呈下降趋势。
|
Download:
|
| 图 3 2005—2017年中国城市生态效率变异系数变化趋势 Fig. 3 Trend of variation coefficient of urban eco-efficiency in China from 2005 to 2017 | |
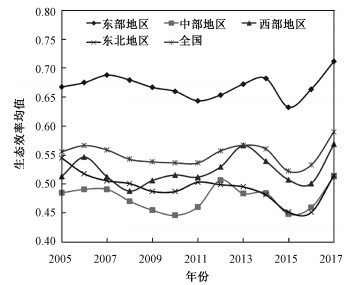
为了对比中国城市生态效率的地区间差异,将中国285个城市划分为东部地区、中部地区、西部地区和东北地区,并绘制2005—2017年全国及4大经济区域城市生态效率均值变化趋势图(图 4)。
|
Download:
|
| 图 4 2005—2017年中国4大区域城市生态效率均值变化 Fig. 4 The change of average urban eco-efficiency of four major regions in China from 2005 to 2017 | |
从区域层面来看,东、中、西、东北4个区域的城市平均生态效率分别为0.669、0.476、0.523、0.495,全国城市平均生态效率为0.551。东部地区高于全国平均水平,而中部、西部和东北地区低于全国平均水平。从图 4中可以看出,4大区域的城市生态效率均值与全国城市生态效率均值的变化趋势和变化过程相一致,其中东部地区的城市生态效率始终高于其他3大地区,整体上呈现东部地区>西部地区>东北地区>中部地区的态势。东部地区一直以来是中国经济最发达的地区,资源丰富,资本、劳动力均向东部地区集聚,新兴产业不断涌现带动了地区发展,因此生态效率与其他区域相比较高。而西部地区虽然经济发展水平不高,但污染物排放量相对较少,因此生态效率相对较高。东北地区经济发展方式较为粗放,以资源密集型产业为主且环境污染较严重,因此生态效率较低。中部地区在这个经济发展过程中处于国家优惠扶持政策的边缘化位置,区域内部缺少合作,经济发展不能形成整体合力,因而经济发展缓慢,进而导致生态效率较低。
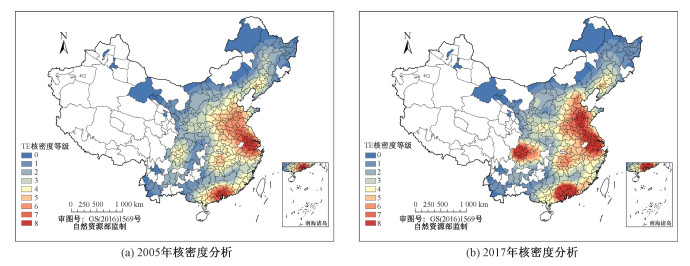
2.2.2 城市间差异为更清楚地反映中国城市生态效率的空间分异特征,根据计算得到的全国285个城市的生态效率,绘制2005和2017年中国城市生态效率分布图(图 5)及核密度图(图 6)。

|
Download:
|
| 图 5 2005—2017年中国城市生态效率空间分布对比 Fig. 5 Spatial distribution of urban eco-efficiency in China from 2005 to 2017 | |
|
Download:
|
| 图 6 2005—2017年中国城市总体生态效率分布格局对比 Fig. 6 Kernel density analysis of urban eco-efficiency in China from 2005 to 2017 | |
由图 5可以看出,2005年中国城市生态效率普遍较低,生态效率高于0.8的城市数量较少,主要分布在珠三角地区、长三角地区、海峡西岸城市群地区、山东等东部沿海地区及黑龙江、内蒙古、云南和贵州等省区。生态效率处于0.6~0.8的城市数量也较少,主要分布于东部沿海地区。生态效率处于0.4~0.6的城市最多,共有132个,在东部、中部、西部、东北地区均有较多分布。生态效率低于0.4的城市较多,主要分布在中西部地区。与2005年相比,2017年中国城市生态效率整体处于较高水平状态,全国城市总体生态效率有较大幅度的提高。2017年生态效率高于0.8的城市数量增多,主要分布在珠三角地区、北部湾地区、长三角地区、长江中游城市群地区、山东半岛城市群地区和黑龙江、吉林、辽宁、内蒙古地区。生态效率处于0.6~0.8的城市较2005年显著增多,增至92个,在东部沿海地区分布最为集中。生态效率处于0.4~0.6的城市数量较2005年减少,主要分布于中西部、东北地区。生态效率低于0.4的城市主要分布在中部地区和东北地区,其数量较2005年减少,其中以西部地区减少最为显著。
从图 6可以看出,2005年城市生态效率处于较高水平的城市主要分布在珠三角地区、长三角地区、山东半岛地区,而东北地区、内蒙古、甘肃、云南和贵州等地区的生态效率处于较低水平。与2005年相比,2017年城市生态效率处于较高水平的范围明显增大,生态效率处于较高水平的城市主要分布在珠三角、长三角、山东半岛、河北、河南和四川等地区,其他地区仍处于较低水平。
2.3 城市生态效率影响因素分析 2.3.1 变量的选取为进一步探讨影响生态效率的因素,基于生态效率的概念和对已有文献及理论的研究,本文选取经济发展水平、产业结构、工业化水平、技术水平、对外开放水平和城镇化水平6类影响因素作为解释变量,以2005—2017年的城市生态效率值作为被解释变量,运用面板回归模型(式(7))对影响因素进行考察。各因素表征指标如表 3所示。数据来源于相关年份的《中国城市统计年鉴》。为保证数据的平稳性,在回归之前将数据进行对数化处理。
|
|
表 3 城市生态效率影响因素 Table 3 Definition of explanatory variables for urban eco-efficiency |
为研究城市生态效率的影响因素,需要通过检验选择最佳模型进行拟合。首先运行混合面板回归模型,表 4第2列为混合OLS回归结果,可以看到所有变量的系数均显著。随后进行固定效应(fixed effects,FE)回归分析,可以看到各个解释变量系数均显著;自相关系数φ为0.760 9,说明个体效应显著,城市间差异明显;F检验结果表明固定效应模型拟合明显优于总体混合回归模型。随后运用随机效应(random effects,RE)回归模型进行拟合,结果可以看到各个解释变量系数均显著;自相关系数φ为0.653 2,说明存在显著的个体效应,城市间异质性明显;且LM检验结果表明随机效应模型明显优于总体混合回归模型。根据Hausman检验结果,判定为固定效应模型优于随机效应模型,因此下文基于固定效应模型的回归结果来探析城市生态效率的影响因素。
|
|
表 4 面板模型回归结果 Table 4 Results of panel regression models |
从固定效应回归结果来看,所选定的影响因子均通过显著性检验,表明城市生态效率高低受多种因素的综合影响。其中,经济发展水平(lnrgdp)、对外开放水平(lnFDI)均对城市生态效率提升有显著促进作用。产业结构(lnSecond)指标的回归结果表明产业升级对于提高城市经济效益有着显著的正向促进作用。科技水平(lnSCI)对城市生态效率有着显著的正向促进作用;城市科技水平高,对于环境的保护和治理能力更强,科技对于经济发展的促进作用明显,进而促进城市生态效率的提高。城镇化水平(lnurban)较高的区域,其生态效率也相对较高,因为经济的集聚和集约发展,提高了城市的经济运行绩效,加之城市的管理水平较强,人们的环保意识较高,因而城市的生态效率较高。城市工业化水平(lnindust)的回归系数为负,且通过显著性检验,说明工业规模扩张对城市生态效率有着显著的反向抑制作用;城市的工业规模越大,相应地资源消耗量也越大,环境污染亦较为严重,因而降低了城市的生态效率。
3 结论与讨论基于非期望产出超效率SBM模型,本文对2005—2017年中国285个地级以上城市的生态效率进行分析,并运用面板回归模型检验城市生态效率的影响因素。主要结论如下:
1) 2005—2017年间中国城市生态效率波动较小,整体呈现上升的趋势,且城市间的生态效率差异逐渐缩小。城市生态效率的提升主要源于城市纯技术效率的提升,城市的管理有效,资源配置较为合理,促进城市生态效率的提升,而规模效率对生态效率的提升起着负向作用,城市间的合作有待加强。
2) 从区域层面来看,全国4大板块的城市生态效率与全国城市平均生态效率的变化过程和趋势基本一致。东部地区生态效率高于全国均值,中部、西部和东北部地区的生态效率均低于全国均值,整体上呈现东部地区>西部地区>东北地区>中部地区的态势。
3) 全国城市生态效率时空格局演化特征明显。2005年生态效率较高的城市主要分布在珠三角、长三角、山东等省区,其他大部分地区城市生态效率处于较低水平;2017年城市生态效率较高的空间范围明显扩展,珠三角、长三角、山东、河南、河北、湖北和四川等地区的生态效率处于较高水平,其他地区仍处于较低水平。
4) 面板回归模型对城市生态效率影响因素的研究结果表明,城镇化水平、经济发展水平、对外开放水平、科技水平和产业结构对城市生态效率的提升起着显著的促进作用,而工业化水平则起负向抑制作用。
基于以上的研究结论,结合中国发展的实际情况,本文认为提高城市生态效率,要促进城市经济均衡发展,统筹发展战略与政策,缩小地区间的差距,调整产业结构,发展绿色产业,注重环境与经济之间的均衡发展,进而提升城市生态效率。
随着生态文明思想的推进和对区域高质量发展模式的关注,从多维视角刻画经济发展与资源环境耦合协调机理的研究也会倍受学术界和管理部门的重视。本文从经济、资源、环境3方面选取指标,构建城市生态效率评价指标体系,但受数据可获得性的限制,资源投入方面未引入矿产资源消耗数据,环境方面未来亦可考虑增加不同种类大气环境污染物浓度等指标来进行分析。
| [1] |
Schaltegger S, Sturm A. Ökologische rationalität[J]. Die Unternehmun, 2001, 2(3): 288-289. |
| [2] |
WBCSD. Eco-efficient leadership for improved economic and environmental performance[M]. Geneva, Switzerland: WBCSD, 1996: 3-16.
|
| [3] |
Fussler C. Development of industrial ecological efficiency[J]. Industry and Environment (Chinese version), 1995, 17(4): 71-74. |
| [4] |
潘兴侠. 我国区域生态效率评价、影响因素及收敛性研究[D]. 南昌: 南昌大学, 2014.
|
| [5] |
韩增林, 王倩雯, 刘天宝, 等. 中国生态效率时空动态分布与演进趋势[J]. 统计与决策, 2019, 35(22): 85-88. |
| [6] |
刘轩志, 赵文莉. 黄河流域沿线省份生态效率测度[J]. 区域治理, 2019(45): 117-119. Doi:10.3969/j.issn.2096-4595.2019.45.042 |
| [7] |
邓霞. 区域生态效率评价研究: 以长江经济带为例[J]. 价格理论与实践, 2019(11): 133-137. |
| [8] |
马骏, 曹芳, 周盼超. 长江经济带城市生态效率演变及驱动因素分析[J]. 资源与产业, 2020, 22(1): 32-40. |
| [9] |
易杏花, 刘锦钿. 我国西部地区生态效率评价及其影响因素分析[J]. 统计与决策, 2020, 36(1): 105-109. |
| [10] |
任宇飞, 方创琳. 京津冀城市群县域尺度生态效率评价及空间格局分析[J]. 地理科学进展, 2017, 36(1): 87-98. |
| [11] |
车国庆. 中国地区生态效率研究: 测算方法、时空演变及影响因素[D]. 长春: 吉林大学, 2018.
|
| [12] |
郝帅. 中国大陆生态效率评价与预测研究[D]. 辽宁大连: 辽宁师范大学, 2018.
|
| [13] |
郑德凤, 郝帅, 孙才志. 基于DEA-ESDA的农业生态效率评价及时空分异研究[J]. 地理科学, 2018, 38(3): 419-427. |
| [14] |
侯孟阳, 姚顺波. 1978-2016年中国农业生态效率时空演变及趋势预测[J]. 地理学报, 2018, 73(11): 2168-2183. Doi:10.11821/dlxb201811009 |
| [15] |
张新林, 仇方道, 王长建, 等. 长三角城市群工业生态效率空间溢出效应及其影响因素[J]. 长江流域资源与环境, 2019, 28(8): 1791-1800. |
| [16] |
李根, 刘家国, 李天琦. 考虑非期望产出的制造业能源生态效率地区差异研究: 基于SBM和Tobit模型的两阶段分析[J]. 中国管理科学, 2019, 27(11): 76-87. |
| [17] |
陈翔, 肖序. 中国工业产业循环经济效率区域差异动态演化研究与影响因素分析: 来自造纸及纸制品业的实证研究[J]. 中国软科学, 2015(1): 160-171. Doi:10.3969/j.issn.1002-9753.2015.01.017 |
| [18] |
任宇飞, 方创琳, 蔺雪芹. 中国东部沿海地区四大城市群生态效率评价[J]. 地理学报, 2017, 72(11): 2047-2063. Doi:10.11821/dlxb201711010 |
| [19] |
王敏, 张晓平. 基于PCA-DEA模型的中国省际生态效率研究[J]. 中国科学院大学学报, 2015, 32(4): 520-527. |
| [20] |
Vogtländer J G, Bijma A, Brezet H C. Communicating the eco-efficiency of products and services by means of the eco-costs/value model[J]. Journal of Cleaner Production, 2002, 10(1): 57-67. Doi:10.1016/S0959-6526(01)00013-0 |
| [21] |
Burritt R L, Saka C. Environmental management accounting applications and eco-efficiency: case studies from Japan[J]. Journal of Cleaner Production, 2006, 14(14): 1262-1275. Doi:10.1016/j.jclepro.2005.08.012 |
| [22] |
戴铁军, 陆钟武. 钢铁企业生态效率分析[J]. 东北大学学报, 2005, 26(12): 1168-1173. |
| [23] |
涂正革, 刘磊珂. 考虑能源、环境因素的中国工业效率评价: 基于SBM模型的省级数据分析[J]. 经济评论, 2011(2): 55-65. |
| [24] |
Zhang X P, Li Y F, Wu W J. Evaluation of urban resource and environmental efficiency in China based on the DEA model[J]. Journal of Resources and Ecology, 2014, 5(1): 11-19. Doi:10.5814/j.issn.1674-764x.2014.01.002 |
| [25] |
关伟, 许淑婷. 中国能源生态效率的空间格局与空间效应[J]. 地理学报, 2015, 70(6): 980-992. |
| [26] |
韩增林, 吴爱玲, 彭飞, 等. 基于非期望产出和门槛回归模型的环渤海地区生态效率[J]. 地理科学进展, 2018, 37(2): 255-265. |
| [27] |
Tone K. A slacks-based measure of efficiency in data envelopment analysis[J]. European Journal of Operational Research, 2001, 130(3): 498-509. Doi:10.1016/S0377-2217(99)00407-5 |
| [28] |
方创琳, 关兴良. 中国城市群投入产出效率的综合测度与空间分异[J]. 地理学报, 2011, 66(8): 1011-1022. |
| [29] |
王恩旭, 武春友. 基于超效率DEA模型的中国省际生态效率时空差异研究[J]. 管理学报, 2011, 8(3): 443-450. Doi:10.3969/j.issn.1672-884X.2011.03.018 |
| [30] |
李青松, 徐国劲, 邓素君, 等. 基于DEA-Malmquist-Tobit模型的河南省生态效率研究[J]. 环境科学与技术, 2016, 39(4): 194-199. |
| [31] |
常新锋, 管鑫. 新型城镇化进程中长三角城市群生态效率的时空演变及影响因素[J]. 经济地理, 2020, 40(3): 185-195. |
| [32] |
王兆峰, 刘庆芳. 长江经济带旅游生态效率时空演变及其与旅游经济互动响应[J]. 自然资源学报, 2019, 34(9): 1945-1961. |
| [33] |
孟凡生, 邹韵. 中国生态能源效率时空格局演化及影响因素分析[J]. 运筹与管理, 2019, 28(7): 100-107. |
| [34] |
杨勇, 邓祥征. 中国城市生态效率时空演变及影响因素的区域差异[J]. 地理科学, 2019, 39(7): 1111-1118. |
| [35] |
张新林, 仇方道, 谭俊涛, 等. 中国工业生态效率时空分异特征及其影响因素解析[J]. 地理科学, 2020, 40(3): 335-343. |
| [36] |
付丽娜, 陈晓红, 冷智花. 基于超效率DEA模型的城市群生态效率研究: 以长株潭"3+5"城市群为例[J]. 中国人口·资源与环境, 2013, 23(4): 169-175. Doi:10.3969/j.issn.1002-2104.2013.04.027 |
| [37] |
Tone K. A slacks-based measure of super-efficiency in data envelopment analysis[J]. European Journal of Operational Research, 2002, 143(1): 32-41. Doi:10.1016/S0377-2217(01)00324-1 |
| [38] |
Tone K, Tsutsui M. Applying an efficiency measure of desirable and undesirable outputs in DEA to US electric utilities[J]. Journal of CENTRUM Cathedra: The Business and Economics Research Journal, 2011, 4(2): 236-249. Doi:10.7835/jcc-berj-2011-0061 |
 2021, Vol. 38
2021, Vol. 38 


