人类的生产和生活以及社会的发展都依赖能源,目前全球的能源供应主要来自煤、石油、天然气等传统化石能源。化石能源会造成环境的污染和破坏,因此世界各国一直致力于对新能源的探索研究。可控核聚变是能量巨大、原材料取之不尽、干净、安全的新能源[1]。
磁约束的托克马克装置是可控的核聚变反应堆。聚变堆中面向等离子体的第一壁表面需要承受高强度的中子辐照和表面热负荷。采用流动的液态金属作为面向等离子体第一壁可以解决固态第一壁的很多不足,是未来托克马克装置中第一壁的重要可能途径[2]。实现将液态金属作为面向等离子体第一壁,首要任务是需要弄清液态金属液膜在外加磁场环境下的流动和换热特性。导电流体通过磁场时将产生诱导电流,此诱导电流与磁场相互作用在流体中产生一个与流动方向相反的洛仑兹(Lorentz)体积力,也即磁流体动力学(magnetohydrodynamics, MHD)效应[3]。齐天煜等[4]曾进行过展向磁场作用下液态金属GaInSn多层膜流实验研究,研究液态金属在平板上的铺展特性,表明磁场对液态金属流动产生很强的抑制性和阻尼性。液态金属的铺展除采用平板结构以外,也有学者探索微槽道结构,Xu等[5],Fiflis等[6]和Ruzic等[7]以聚变堆限制器为研究背景,提出可以基于LiMIT模型,利用热电磁流体力学(thermoelectric magnetohydrodynamics, TEMHD)效应驱动液体锂在微槽道中流动,并进行相关实验,初步的研究结果表明该方法可行。Xu等[8-9]以面向等离子体第一壁作为研究背景,利用TEMHD效应,驱动液态锂在竖直放置的实验板微槽道中流动,并测得液态锂的平均流速。Ren等[10]在HT-7装置上进行液态锂微槽道流动的实验研究,测得锂的平均流速并拟合了平均流速的经验关系式。Kaita等[11]通过实验研究以液态锂作为工质的面向等离子体部件。此外Hu等[12-13]为了实现液态锂在限制器壁面形成均匀铺展,设计微通道结构的分流器,并在EAST装置上进行了相关实验。
虽然目前已经有学者在外加磁场条件下,对液态金属在微槽道中的流动进行了相关的研究,但前人的工作主要关注液态金属的流动状态,对换热规律的研究较少。研究在强磁场环境下,液态金属在微槽道中的流动与换热特性,以及研究磁场对液态金属在微槽道中的流动与换热的影响对聚变堆的安全稳定运行具有重要意义。本文将开展无磁场条件下液态金属在微槽道中的流动与换热特性研究,完成无磁场条件下的实验之后,把实验段整体放入强磁场下,研究在外加磁场条件下液态金属在微槽道中的流动与换热特性,并对比有磁场和无磁场2种工况的区别,获得磁场对液态金属在微槽道中的流动与换热的影响规律。
1 实验装置与方法 1.1 实验装置液态金属微槽道流动与换热的实验系统如图 1所示,包括氩气驱动系统,微槽道实验段,电加热系统,温度测量系统,流量测量系统,强磁场装置等。图 2给出微槽道实验板实物图,实验板采用无磁性的316 L不锈钢材质加工而成,实验板总长280 mm,总宽61 mm,高35 mm,壁厚10 mm,实验板内部有20条微槽道,每条槽道宽1 mm、深2 mm、长220 mm。

|
Download:
|
| 图 1 实验装置图 Fig. 1 Schematic diagram of experimental apparatus | |

|
Download:
|
| 图 2 实验板实物图 Fig. 2 Diagram of microchannel experiment plate | |
液态金属通过氩气的驱动,自下而上流入实验板。为了使液态金属能够均匀地流入20条槽道,实验板的入口处设计成类似三角形,并在槽道入口处加盖板,强迫液态金属进入微槽道。同时为了使液态金属顺利从实验板中流出,出口处设计成漏斗状。加热器采用宽61 mm、长220 mm的金属加热片,加热片紧密贴合在实验板底部。实验板的侧面有3组小孔,小孔孔径1.5 mm,深度20 mm,用于布置热电偶。小孔内填充铜粉固定热电偶。此外在实验板的入口和出口管道处分别布置2个热电偶。为了减小散热对实验结果的影响,在实验板的四周侧面和底部使用保温棉进行保温处理。
1.2 实验介质与研究方法实验采用液态金属镓铟锡合金(Ga68%In20% Sn12%)作为工质,镓铟锡合金的物性参数如表 1所示。
|
|
表 1 液态金属合金物性参数 Table 1 Physical properties of liquid metal (GaInSn) |
实验所用的热电偶均为K型热电偶,热电偶和安捷伦数据采集器Agilent-34970A相连,用以采集温度数据。通过使用傅里叶定律,根据实验板两侧一定距离的温差和不锈钢的导热系数,求得实验板内部的热流密度。换热量通过液态金属的入口和出口的温差,结合液态金属的比热容和质量流量算得加热功率。为精确地测得液态金属的流量,实验台中配备了高精度的气压表和阀门用于控制液态金属的流量。在无磁场条件下的实验中,实验变量包括施加电源功率,功率大小分别为10、20、30 W 3组,驱动气压大小为0.066~0.078 MPa。外加磁场大小为0~1 T。
2 液态金属膜流流动实验结果分析 2.1 液态金属膜流铺展结果聚变堆中需要将流动的液态金属作为面向等离子体第一壁,首先需要实现液态金属在壁面上的均匀铺展。本实验的重点之一是探究液态金属在微槽道实验板表面的铺展特性。同时,为了后续采集实验数据的准确性,本实验也需要液态金属在实验板上实现均匀铺展。实验中利用氩气驱动液态金属,通过氩气的压力,将液态金属压入实验板中的微槽道,同时通过控制气压,调节液态金属的流量与流速。
图 3(a)~3(c)分别是驱动压力为0.066、0.078和0.072 MPa时液态金属在实验板中的铺展现象。由图 3(a)所示,当驱动气压较小时,液态金属的流量小、流速慢,又由于液态金属的表面张力较大,使得在槽道出口处液态金属不能均匀地铺展,产生了一个缺口。由图 3(b)所示,当气压过大时,液态金属的流量大,流速快。此时槽道的出口处实现了均匀铺展,但是由于流速过大,液态金属以较大的速度流入实验板,在槽道入口处冲刷产生了一片未铺展区域,同时在实验板上的流体呈现紊乱的流动状态。

|
Download:
|
| 图 3 不同驱动压力下液态金属在实验板中的铺展现象 Fig. 3 Spreading characteristics of liquid metal in experimental plate under different driving pressures | |
图 3(c)是较为理想的铺展,此时液态金属在实验板的所有区域都实现了均匀铺展,并且流动平稳。通过多次实验测试,发现当驱动气压在0.07 MPa左右时液态金属在实验板中的铺展效果较好,此时的流量在30~100 g/s,对应的流速为0.04~0.30 m/s,微槽道结构证明能够实现液态金属自由表面全液面均匀铺展。
2.2 液态金属流动阻力分析实验中液态金属由氩气驱动,储液罐中的气压是实验系统中的总动力来源。在实验系统中,产生压降的因素有:克服重力、管道沿程损失、实验板入口处局部损失、金属液膜流动剪切应力以及克服由于MHD效应产生的流动阻力。将以上5种因素产生的压降分别记为ΔPg、ΔPf、ΔPm、ΔPv、ΔPB,将总压(驱动压力)记为ΔP。存在如下关系
| $ \Delta P_{g}+\Delta P_{f}+\Delta P_{m}+\Delta P_{v}+\Delta P_{B}=\Delta P. $ | (1) |
1 )克服重力压降
令实验板与储液罐液面的高度差为h,则ΔPg=ρgh。在本实验平台中,h=1.05 m,结合工质(镓铟锡)的密度可以算得ΔPg=65 542 Pa。
2) 管道沿程损失
根据伯努利方程
| $ \left(\frac{V^{2}}{2 g}+z+\frac{p}{\rho g}\right)_{1}=\left(\frac{V^{2}}{2 g}+z+\frac{p}{\rho g}\right)_{2}+h_{f}. $ | (2) |
式中hf是沿程损失。由于管道内的流动可以近似视为定常流动,因此有
| $ h_{f}=\frac{p_{1}-p_{2}}{\rho g}=\frac{\Delta P_{f}}{\rho g}. $ | (3) |
达西-魏思贝奇阻力公式
| $ h_{f}=\lambda_{f} \frac{l}{d} \frac{V_{f}^{2}}{2 g}. $ | (4) |
式中:l、d、Vf、λf分别表示管道长度、直径、管内流态平均流速以及达西摩擦因子。实验中管道内部的流速较小,但由于工质中存在杂质扰动,因此视为湍流。对于达西摩擦因子λf,由布拉修斯公式可得
| $ \lambda_{f}=\frac{0.316\ 4}{R e^{0.25}} . $ | (5) |
联立式(3)~式(5)可得
| $ \Delta P_{f}=\lambda_{f} \frac{l}{d} \frac{1}{2} \rho V_{f}^{2}=\frac{0.316\ 4}{R e^{0.25}} \frac{l}{2 d} \rho V_{f}^{2}. $ | (6) |
3) 入口处局部损失
金属流体在流动过程中,局部损失主要产生在实验板的入口处。工质在入口处的流动较复杂,经历了多次流道面积变化、流速方向变化等过程。实验板的入口处存在一个深度为5 mm的缓冲储液池,在储液池上方添加盖板,盖板覆盖了储液池的全部区域以及微槽道表面前端20 mm的区域。由于入口处添加了盖板,金属流体在入口处流动可视为在20条方管中流体,方管尺寸为1 mm×2 mm,此处存在较大的局部损失。
| $ h_{m_{1}}=\lambda_{m} \frac{l_{m}}{d_{h}} \frac{V_{m}^{2}}{2 g}. $ | (7) |
式中:lm、dh分别为方管长度(本实验中为20 mm)以及方管水力直径。方管尺寸为a=1 mm,b=2 mm,水力直径
| $ d_{h}=\frac{2 a b}{a+b} . $ | (8) |
水力直径雷诺数
| $ \Delta P_{m_{1}}=\lambda_{m} \frac{l_{m}}{d_{h}} \frac{V_{m}^{2}}{2} \rho. $ | (9) |
在实验板的入口处流道面积发生变化,这也会产生局部损失ΔPm2。此处的损失因子
| $ K_{m_{2}}=0.42\left(1-\frac{A_{1}^{2}}{A_{2}^{2}}\right), $ | (10) |
| $ h_{m_{2}}=K_{m} \frac{V_{m}^{2}}{2 g}. $ | (11) |
式中:A1、A2分别为20条方管的流道面积和储液池的最大横截面积。由于存在
| $ h_{m_{2}}=\frac{\Delta P_{m_{2}}}{\rho g}, $ | (12) |
联立式(10)~式(12)可得
| $ \Delta P_{m_{2}}=0.21\left(1-\frac{A_{1}^{2}}{A_{2}^{2}}\right) V_{m}^{2} \rho. $ | (13) |
流速方向引起的局部损失因子

|
(14) |
式中:右边①部分表示此处存在流道面积的扩大,②部分是由于流速发生90°转折。在本实验中Km3≅1.98。于是得到
| $ \Delta P_{m_{3}}=K_{m_{3}} \frac{V_{m}^{2} \rho}{2}. $ | (15) |
综上可求得ΔPm=ΔPm1+ΔPm2+ΔPm3。
4) 金属液膜流动剪切应力
金属液膜在流动时,为了克服液膜流动时的剪切应力τx,会产生压降ΔPv。此时存在
| $ \int \Delta P_{v} \cdot \mathrm{d} S_{1}=\int \mu \frac{\partial \boldsymbol{u}}{\partial \boldsymbol{n}} \cdot \mathrm{d} S_{2}. $ | (16) |
式中:u、n分别为液膜的速度以及流速的法线方向;S1、S2分别为ΔPv的作用面积和液膜的铺展面积。在本实验中为无滑移边界条件,当流动稳定时近似等于
| $ \Delta P_{v} S_{1}=\mu \frac{\Delta \boldsymbol{u}}{\Delta \boldsymbol{n}} S_{2}. $ | (17) |
由式(17)可得
| $ \Delta P_{v}=\mu \frac{\Delta \boldsymbol{u}}{\Delta \boldsymbol{n}} \frac{S_{2}}{S_{1}}. $ | (18) |
5) MHD效应产生的流动阻力
液态金属在磁场中流动时由于MHD效应的存在,会产生一个与流动方向相反的洛伦兹力,克服该洛伦兹力会消耗一部分驱动压力。当计算得到克服重力、管道沿程损失、局部损失以及金属液膜流动剪切应力所产生的压降ΔPg、ΔPf、ΔPm、ΔPv之后,通过关系式
| $ \Delta P_{B}=\Delta P-\left(\Delta P_{g}+\Delta P_{f}+\Delta P_{m}+\Delta P_{v}\right), $ | (19) |
可以计算得到克服MHD效应所产生的压降。
当驱动压力为0.076 MPa,磁场强度分别为0、0.1、0.5和1.0 T时,液态金属的流量分别为125.3、123.8、111.7和99.2 g/s。结合工质的物性参数以及实验平台的相关参数,可以计算得到各工况下的ΔPg、ΔPf、ΔPm、ΔPv以及ΔPB,结果如表 2所示。
|
|
表 2 不同磁场强度下压力损失 Table 2 Pressure drop under different magnetic field intensitiesPa |
需要注意的是,当磁场强度为0 T时,ΔPB应该为0,而实际计算结果为62 Pa,这是由于实验误差以及数据处理误差所致。例如在管道与储液罐的接口以及储液罐内部的管道均会产生局部损失,由于这些压降损失较小,在计算时将其忽略,因此导致0 T时ΔPB不为0。总体而言,从表 2所示的实验结果可以看出,随着磁场强度的增大,各工况下的ΔPB(克服MHD效应所产生的压降)逐渐增大。压降的大小直接反映出流动阻力的大小,克服MHD效应所产生的压降随着磁场强度的增大逐渐增大,说明磁场增大了金属流体的流动阻力。
3 液态金属膜流换热实验结果分析 3.1 无磁场强迫对流换热特性对流换热系数是衡量对流换热强弱的重要特征变量。实验中通过采集液态金属的进出口温度以及流量通过牛顿冷却公式计算出平均换热系数
| $ Q=W C_{p}\left(T_{\text {out }}-T_{\text {in }}\right), $ | (20) |
| $ Q=h A\left(T_{s}-T_{f}\right), $ | (21) |
| $ h=\frac{Q}{A\left(T_{s}-T_{f}\right)}=\frac{W C_{p}\left(T_{\text {out }}-T_{\text {in }}\right)}{A\left(T_{s}-T_{f}\right)}. $ | (22) |
式中:W、Cp、Tout、Tin分别是镓铟锡(GaInSn)的质量流量、比热容、出口温度和入口温度。A是微槽道表面换热面积,Ts是根据微槽道实验板内部温度分布插值得到槽顶和槽底的平均温度,Tf是流体平均温度由出入口液态金属平均温度计算得到。
Nu数分别是表征对流换热特征,计算得到平均换热系数后,由Nu数的定义式
| $ N u=\frac{h L}{\lambda_{\mathrm{GaInSn}}}, $ | (23) |
可以计算得到平均Nu数。λGaInSn是镓铟锡的导热系数,L是特征长度,本文中用水力直径作为特征长度。水力直径定义如下
| $ D_{h}=\frac{4 A_{f}}{l}, $ | (24) |
式中:Af为流道横截面积,l为湿润周长。
在本文的微槽道研究中,槽道流动表面为自由表面流动,引入We数表征惯性力和表面张力之比的无量纲特征数,其定义式为
| $ W e=\frac{\rho v^{2} L}{\sigma}. $ | (25) |
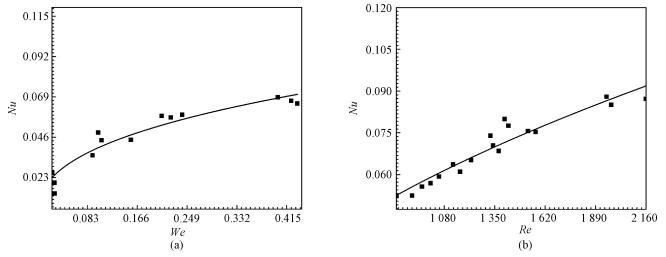
式中:ρ、v、σ分别为镓铟锡的密度、流速以及表面张力系数。当流速较小的情况下,We数小于1,说明液态金属在流动时受到表面张力的影响要大于惯性力的影响,所以选择拟合Nu数和We数之间的关系曲线;当流速较大的情况下,We数大于1,说明液态金属在流动时受到惯性力的影响要大于表面张力的影响。图 4(a)是实验板中心处的局部Nu数与We数的关系曲线图,图 4(b)是实验板中心处的局部Nu数与Re数的关系曲线图。其中Re数的定义式为
|
Download:
|
| 图 4 实验板中心处Nu与We及Re关系曲线 Fig. 4 Local Nusselt numbers of microchannel plate under different Weber numbers and Reynolds numbers | |
| $ R e=\frac{v \rho L}{\mu} $ | (26) |
通过调节加热功率和驱动气压,得到不同的加热热流密度和流速。实验结果如图 4(a)和4(b)所示,实验板的中心处的Nu数随We数和Re数的增大而增大,说明液态金属与实验板之间的对流换热随着We数和Re数的增大而增大。从We数和Re数的定义式中可以看出,当实验工质确定时,影响We数和Re数大小的因素是流体的流速,当流速增大时,液态金属以更大的速度冲刷实验板,所以对流换热增强。从图 4(a)和4(b)拟合的曲线可以看出,Nu数与We数及Re数总体呈幂指数关系。
3.2 磁场影响下强迫对流换热特性研究在外加磁场条件,液态金属与微槽道实验板之间的换热特性是本实验的重点。实验中通过改变磁场强度,研究在相同驱动压力下磁场对换热特性的影响。实验中驱动压力恒定为0.070、0.072、0.076 MPa 3组,磁场强度的变化范围为0~1 T。实验所用磁场由电磁铁产生,属于均匀磁场,磁场均匀度达90%以上,最大磁场强度可达1.7 T。
导电流体在磁场中运动,与磁场相互作用产生诱导电流J(J=Vi×B),诱导电流和磁场相互作用在流体内部产生洛伦兹力F(F=J×B)。式中B为磁场强度,设B=Bxex+Byey+Bzez(ex, ey, ez分别为笛卡尔坐标系单位向量),vi=uiex+uiey+uiez。那么F=(Vi×B)×B。磁场方向角度ϕ,tanϕ=By/Bx,在本实验属于三维流动,可以得到以下控制方程
连续性方程
| $ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0. $ | (27) |
动量守恒方程
| $ \begin{gathered} \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z}= \\ -\frac{1}{\rho} \frac{\partial p}{\partial x}+v \nabla^{2} u+\frac{\boldsymbol{B}^{2}}{\rho}\left(v \sin \emptyset \cos \emptyset-u \sin ^{2} \emptyset\right). \end{gathered} $ | (28) |
能量守恒方程
| $ \frac{\partial T}{\partial t}+u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y}+w \frac{\partial T}{\partial z}=\alpha \nabla^{2} T. $ | (29) |
实验中所用磁场方向为水平磁场,磁场方向与主流方向垂直,所以ϕ=0。从方程中可以得到产生的洛伦兹力平行于流体流动方向,且与流动方向相反,从而对流体的流动产生抑制作用。且流速越大,洛伦兹力越大,抑制效果越强,即MHD效应。
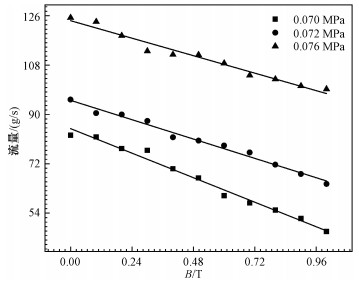
图 5是在3组(0.070、0.072、0.076 MPa)驱动压力下,液态金属的流量随磁场强度的变化趋势图。通过图 5可以明显看出,随着磁场强度的增大流量逐渐减小,即随着磁场的增强,液态金属的流动受到抑制,实验结果与理论相符。同时由图 5可以看出,流量与磁场强度整体呈线性关系。
|
Download:
|
| 图 5 流量随磁场强度变化趋势 Fig. 5 The mass flow rate of liquid metal under the influence of a magnetic field | |
哈特曼数是表征电磁力和黏滞力之比的无量纲准则数,其定义式为
| $ H a=\boldsymbol{B} L \sqrt{\frac{\sigma}{\mu}}. $ | (30) |
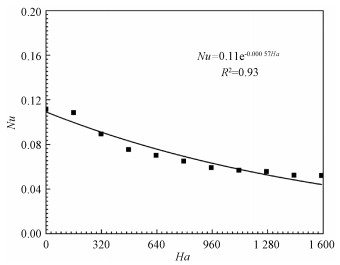
式中:B是磁场强度,L是特征长度,σ是流体的电导率,μ是流体的动力黏度。图 6是驱动压力为0.076 MPa,加热功率为10 W的工况下,实验板的平均Nu数随Ha数的曲线趋势图,两者之间总体呈幂指数关系。从图 6所示的实验结果可以看出,Nu数随着Ha数的增大而减小。Ha数同时也可以表征磁场对导电流体流动的影响,Nu数随着Ha数的增大而减小,说明随着磁场强度的增大对流换热逐渐减弱,即磁场抑制了对流换热。
|
Download:
|
| 图 6 平均Nu数随Ha数变化趋势 Fig. 6 The average Nusselt numbers of microchannel plate under different Hartmann numbers | |
综合分析图 5和图 6所示的实验结果,发现随着磁场强度的增大,液态金属流体的流量逐渐减小,同时换热逐渐受到抑制,可以判断磁场是通过影响流体流动从而影响换热特性。因为随着磁场强度的增大,液态金属的流动受到抑制,流量逐渐减小,平均流速随之减小,流体流过微槽道实验时冲刷实验板的速度减小,从而换热系数也随之减小,表现为磁场抑制对流换热。图 6中0.076 MPa的驱动压力下实验结果可得磁场影响下的换热实验关系式可拟合为
| $ N u=0.11 \mathrm{e}^{-0.000\ 57 H a} . $ | (31) |
从式(31)可以看出,磁场强度增大对微槽道液态金属的流动换热有显著的抑制作用。
4 结论本文研究液态金属在微槽道结构实验板中的铺展特性,证实相比于前人基于平板表面金属膜流的研究[4, 14],微槽道的表面结构有利于液态金属的均匀铺展。当液态金属流入实验板时,通过微槽道的分流,流体均匀地流入每一条槽道,从而形成均匀膜流。液膜的铺展和流动特性受到金属流体的流速影响。流速较小时,金属液膜难以实现完全均匀铺展,流速过大时,不仅会影响液膜铺展,同时液膜流动紊乱。为了得到理想的均匀铺展与平稳流动,需要将流速控制在适当的范围。本实验中的流速在0.04~0.30 m/s范围内。通过分析不同磁场强度下液态金属在流动过程中各部分的压力损失,发现金属流体克服MHD效应所产生的压降随着磁场强度的增大而逐渐增大,说明磁场增大了金属流体的流动阻力。
通过分析无磁场条件下的温度数据可知,在流速较小的情况下,实验板中心处的Nu数会随着We数的增大而增大, 且两者之间呈幂指数关系;在流速较大的情况下,实验板中心处的Nu数与Re数之间呈幂指数关系。通过分析外加磁场条件下的实验数据可知,磁场对换热具有抑制作用,随着Ha数的增大Nu数逐渐减小,且两者呈指数函数关系。实验发现磁场是通过影响流体流动从而影响换热特性。随着磁场强度的增大,液态金属的流动受到抑制,流量逐渐减小,平均流速随之减小,流体流过微槽道实验时冲刷实验板的速度减小,从而换热系数也随之减小,表现为磁场抑制对流换热。
| [1] |
张一鸣, 曾丽萍, 沈欣媛, 等. ITER计划与聚变能发展战略[J]. 核聚变与等离子体物理, 2013, 33(4): 359-365. Doi:10.3969/j.issn.0254-6086.2013.04.012 |
| [2] |
Narula M, Ying A, Abdou M A. A study of liquid metal film flow, under fusion relevant magnetic fields[J]. Fusion Science and Technology, 2005, 47(3): 564-568. Doi:10.13182/FST05-A745 |
| [3] |
Priest E, Forbes T. Magnetic reconnection: MHD theory and applications[M]. Cambridge: Cambridge University Press, 2000: 1-15.
|
| [4] |
齐天煜, 阳倦成, 倪明玖. 展向磁场作用下液态金属GaInSn多层膜流实验研究[J]. 中国科学院大学学报, 2019, 36(3): 320-325. |
| [5] |
Xu W, Curreli D, Andruczyk D, et al. Heat transfer of TEMHD driven lithium flow in stainless steel trenches[J]. Journal of Nuclear Materials, 2013, 438: S422-S425. Doi:10.1016/j.jnucmat.2013.01.085 |
| [6] |
Fiflis P, Morgan T W, Brons S, et al. Performance of the lithium metal infused trenches in the magnum PSI linear plasma simulator[J]. Nuclear Fusion, 2015, 55(11): 113004. Doi:10.1088/0029-5515/55/11/113004 |
| [7] |
Ruzic D N, Xu W, Andruczyk D, et al. Lithium-metal infused trenches (LiMIT) for heat removal in fusion devices[J]. Nuclear Fusion, 2011, 51(10): 102002. Doi:10.1088/0029-5515/51/10/102002 |
| [8] |
Xu W, Fiflis P, Szott M, et al. Vertical flow in the thermoelectric liquid metal plasma facing structures (TELS) facility at Illinois[J]. Journal of Nuclear Materials, 2015, 463: 1181-1185. Doi:10.1016/j.jnucmat.2014.12.045 |
| [9] |
Xu W, Surla V, Jaworski M A, et al. Investigation of the heat transfer in TEMHD driven swirling lithium flow[J]. Journal of Nuclear Materials, 2011, 415(Sup): S981-S984. |
| [10] |
Ren J, Hu J S, Zuo G Z, et al. First results of flowing liquid lithium limiter in HT-7[J]. Physica Scripta, 2014, T159: 014033. Doi:10.1088/0031-8949/2014/T159/014033 |
| [11] |
Kaita R, Majeski R, Gray T, et al. Low recycling and high power density handling physics in the Current Drive Experiment-Upgrade with lithium plasma-facing components[J]. Physics of Plasmas, 2007, 14(5): 056111. Doi:10.1063/1.2718509 |
| [12] |
Hu J S, Zuo G Z, Ren J, et al. First results of the use of a continuously flowing lithium limiter in high performance discharges in the EAST device[J]. Nuclear Fusion, 2016, 56(4): 046011. Doi:10.1088/0029-5515/56/4/046011 |
| [13] |
Zuo G Z, Hu J S, Maingi R, et al. Results from an improved flowing liquid lithium limiter with increased flow uniformity in high power plasmas in EAST[J]. Nuclear Fusion, 2019, 59(1): 016009. Doi:10.1088/1741-4326/aaedcb |
| [14] |
倪明玖, 阳倦成, 任东伟, 等. 聚变堆相关的液态金属膜流初步实验研究[J]. 力学学报, 2018, 50(6): 1379-1386. |
 2021, Vol. 38
2021, Vol. 38 


