2. Shandong Provincial Engineering and Technical Center of Light Manipulations & Shandong Provincial Key Laboratory of Optics and Photonic Device, School of Physics and Electronics, Shandong Normal University, Jinan 250358, China
2. 山东师范大学物理与电子科学学院 山东省光场调控工程技术研究中心&山东省光学与光子器件技术重点实验室, 济南 250358
Third-harmonic (TH) generated by femtosecond filamentation has attracted great attention due to the involved nonlinear processes[1] and its potential applications in remote sensing and supercontinuum generation[2-5]. During the filamentation of fundamental wave (FW) in air, the peak intensity is clamped at 1013~1014 W/cm2. Correspondingly, the peak intensity of TH generated in this process can reach the value that higher than 1012 W/cm2[6]. Due to the strong drive by the filamentation of the FW, the TH pulse keeps synchronization with the FW without the walk-off phenomenon[7], and the characteristics of the TH follow the filamentation dynamics of the FW[8]. It is important for the potential applications to investigate the co-propagation of FW and TH when the initial FW has complicated distribution in space and time. Up to date, several works on the co-filamentation of FW and TH have been reported for the FW with different initial conditions, such as different central wavelengths[9-11], different pulse durations[12], modulation by amplitude mask[13], and introducing plasma grating[14]. In recent years, the nonlinear propagation of femtosecond laser pulses with complex spatial and phase structures, such as Airy beam[15], Bessel beam[16] and optical vortex[17], has been intensively studied. Especially, the optical vortex which has a spiral phase structure and an annular intensity distribution with a singularity, can be used in many potential applications such as optical tweezers[18], optical communication[19] and astronomical observations[20]. The study of the TH generated by the filamentation of femtosecond vortex beam is important not only to the understanding of the nonlinear process of the optical vortex but also to the discovery of new potential applications. However, there have been very few reports on the TH generated by the filamentation of the optical vortex. Although the TH vortex is experimentally reported to be generated by the filamentation of the femtosecond vortex beam in air[21], the maintaining conditions of the two-color vortex, which are important to the applications, are still unknown during this nonlinear co-propagation.
In this paper, we perform simulations on the nonlinear co-propagation of the femtosecond vortex beam and the generated TH vortex in air. The influences of the perturbation distribution and peak power of the initial FW on the evolution of two-color vortex are investigated. Considering the real condition of the femtosecond laser beam, we introduce symmetrical and asymmetrical distributions of the perturbation to the FW in the transverse plane. The keeping conditions of the vortex characteristics, including the annular intensity and the spiral phase distributions, are investigated.
1 Numerical simulationThe equations which are used to simulate the TH generated by the filamentation of femtosecond vortex beam in air[6] are written as
| $ \begin{gathered} \left(\mathrm{i} \frac{\partial}{\partial z}+\frac{1}{2 k_{0}} \nabla_{\perp}^{2}-\frac{k_{\omega}^{\prime \prime}}{2} \frac{\partial^{2}}{\partial t^{2}}\right) E_{\omega}+k_{0} n_{2}\left[\frac { 1 } { 2 } \left(\left|E_{\omega}\right|^{2}+\right.\right. \\ \left.\tau_{k}^{-1} \int_{-\infty}^{t} \mathrm{e}^{-\left(t-t^{\prime}\right) / \tau_{k}}\left|E_{\omega}\left(t^{\prime}\right)\right|^{2} \mathrm{~d} t^{\prime}\right) E_{\omega}+ \\ \left.2\left|E_{3 \omega}\right|^{2} E_{\omega}+E_{\omega}^{* 2} E_{3 \omega}\right]-\frac{k_{0}}{2} \frac{\rho}{\rho_{c}} E_{\omega}+ \\ \frac{\mathrm{i}}{2} \beta_{\omega}^{\left(K_{\omega}\right)}\left|E_{\omega}\right|^{2 K_{\omega}-2} E_{\omega}=0, \end{gathered} $ | (1) |
| $ \begin{gathered} \left(\mathrm{i} \frac{\partial}{\partial z}+\frac{1}{6 k_{0}} \nabla_{\perp}^{2}+\mathrm{i} \Delta \vartheta^{-1} \frac{\partial}{\partial t}-\frac{k_{3 \omega}^{\prime \prime}}{2} \frac{\partial^{2}}{\partial t^{2}}-\Delta k\right) E_{3 \omega}+ \\ 3 k_{0}\left(n_{2}^{3 \omega}\left|E_{3 \omega}\right|^{2} E_{3 \omega}+2 n_{2}\left|E_{\omega}\right|^{2} E_{3 \omega}+\frac{n_{2} E_{\omega}^{3}}{3}\right)- \\ \frac{k_{0}}{6} \frac{\rho}{\rho_{c}} E_{3 \omega}+\frac{\mathrm{i}}{2} \beta_{3 \omega}^{\left(K_{3 \omega}\right)}\left|E_{3 \omega}\right|^{2 k_{3 \omega}-2} E_{3 \omega}=0, \end{gathered} $ | (2) |
| $ \frac{\partial \rho}{\partial t}=\left(\sigma_{\omega}\left|E_{\omega}\right|^{2 K_{\omega}}+\sigma_{3 \omega}\left|E_{3 \omega}\right|^{2 K_{3 \omega}}\right)\left(\rho_{0}-\rho\right), $ | (3) |
where Eω and E3ω describe the electric field envelops of the FW and TH, respectively, and z is the propagation distance. k0=2π/λ0 is the central wave number for the FW with the central wavelength λ0=800 nm. The parameters of the coupled equations are taken from Ref.[6]. The diffraction effect is described by the Laplace operator
The initial distributions of the FW and the TH are written as
| $ \begin{gathered} E_{\omega}(r, t, z=0)=A \frac{r}{r_{0}} \exp \left(-\frac{t^{2}}{2 t_{0}^{2}}\right) \\ \exp \left(-\frac{r^{2}}{2 r_{0}^{2}}\right) \exp \left(\mathrm{i} m_{\omega} \theta\right), \end{gathered} $ | (4) |
| $ E_{3 \omega}(r, t, z=0)=0, $ | (5) |
where, the diameter r0=0.5 mm, pulse duration (FWHM) ΔT=2
| $ A=1+A_{p}, $ | (6) |
where Ap is the amplitude of the initial perturbation. To study the influence of the initial perturbation on the evolution of the two-color vortex, we assume that the perturbation has symmetrical or asymmetrical distribution, respectively. For the symmetrical case, the amplitude of the perturbation is written as
| $ \begin{gathered} A_{p}=\varepsilon\left[\exp \left(-\frac{\left(x-r_{0}\right)^{2}+y^{2}}{2 r_{1}^{2}}\right)+\right. \\ \exp \left(-\frac{\left(x+r_{0}\right)^{2}+y^{2}}{2 r_{1}^{2}}\right)+\exp \left(-\frac{x^{2}+\left(y-r_{0}\right)^{2}}{2 r_{1}^{2}}\right)+\\ \left.\exp \left(-\frac{x^{2}+\left(y+r_{0}\right)^{2}}{2 r_{1}^{2}}\right)\right], \end{gathered} $ | (7) |
where the peak amplitude ε=0.02 is evaluated according to the experimental condition. The beam waist of the perturbation is assumed to be r1=0.15 mm. For the asymmetrical case, the amplitude of the perturbations is written as
| $ A_{p}=\varepsilon \exp \left(-\frac{\left(x-r_{0}\right)^{2}+y^{2}}{2 r_{1}^{2}}\right). $ | (8) |
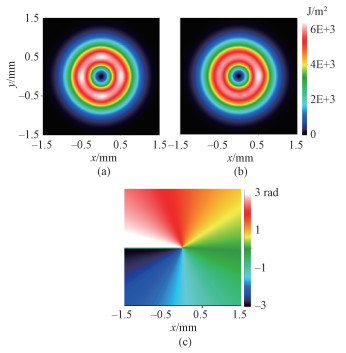
The fluence and phase distributions of the initial FW are plotted in Fig. 1.
|
Download:
|
|
(a) Fluence distribution of the FW with symmetrical perturbation; (b) Fluence distribution of the FW with asymmetrical perturbation; (c) Phase distribution of the FW. Fig. 1 Fluence distribution and phase distribution of the initial FW |
|
For the FW vortex beam with topological charge mω=1, the critical power for self-focusing is Pcr(mω)=2
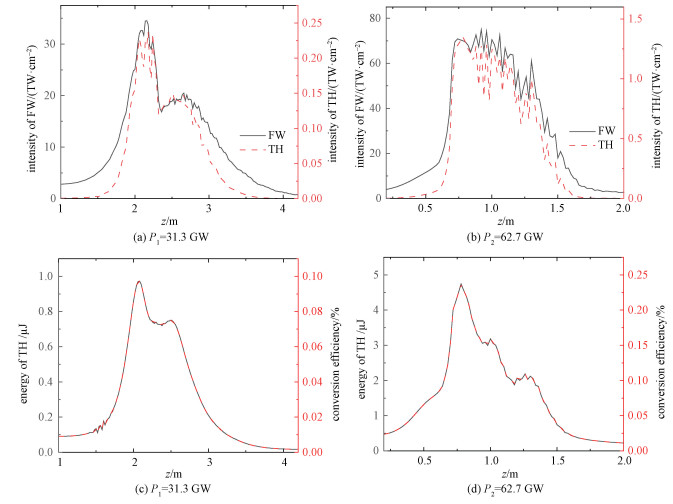
First, we simulate the co-propagation of the FW vortex beam and the generated TH for the initial FW with symmetrical perturbation. The initial distribution of the perturbation is described by Eq. (7), and the initial fluence distribution of the FW is shown in Fig. 1 (a). Figure 2 (a) and 2(b) show the peak intensities of the FW vortex beam and the generated TH for two input peak powers. For both cases, the evolution of the TH intensity follows that of the FW. The TH intensity increases when the filamentation starts, and decreases when the filamentation ends. Correspondingly, the energy and the conversion efficiency of the TH have a similar evolution, as shown in Fig. 2 (c) and 2(d). The energy of the TH increases with the formation of filamentation and is given back to the FW with the termination of filamentation. With the increase of the FW peak power from 31.3 GW to 62.7 GW, both the maximal intensities of the FW and TH have a big increase, from 35 TW/cm2 to 70 TW/cm2, and from 0.25 TW/cm2 to 1.3 TW/cm2, respectively. Correspondingly, the maximal energy of TH increases from 1 μJ to 4.7 μJ, and the maximal conversion efficiency increases from 0.1% to 0.24%, as shown in Fig. 2 (c) and 2(d). On the other hand, with the increase of the power, the onset of the two-color filament becomes earlier, and the filament becomes longer.
|
Download:
|
|
The symmetrical perturbation is initially introduced into the FW vortex beam. Fig. 2 Peak intensities of the FW and the TH, and the energy and conversion efficiency of the TH as a function of propagation distance for two input peak powers |
|
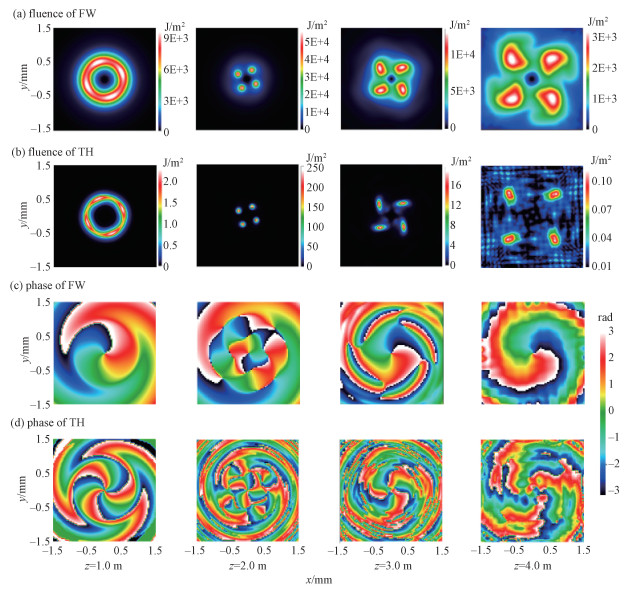
Figure 3 (a) and 3(b) show the fluence distributions of the FW and the TH at several typical propagation distances when the initial FW has symmetrical perturbation and peak power 31.3 GW. From Fig. 3 (a) and 3(b), we can see that during the filamentation (before z=3 m), the annular distributions of the FW and the TH in the transverse plane are kept. The evolution of the TH follows that of the FW. When the FW begins to self-focus, four peaks are formed symmetrically in the annulus (see Fig. 3 (a) z=1.0 m). Then four filaments are formed with the decrease of the radius of the annulus (see Fig. 3 (a) z=2.0 m). The positions of the four filaments are symmetrical and rotational. With the further propagation of the laser, the radius of the annulus increases and the filamentation disperses gradually and tends to termination. Because the TH is mainly generated by the intense FW filaments. The annulus of the TH is changed after the formation of the four filaments (see Fig. 3 (b) z=2.0 m). Most TH energy is concentrated in the four filaments. Moreover, the rotation of the TH filaments keeps synchronous with that of the FW. These results suggest that both the FW and the generated TH can keep the spatial distribution of the vortex in the filamentation regime.
|
Download:
|
|
The symmetrical perturbation is initially introduced into the FW vortex beam which has a peak power of 31.3 GW. Fig. 3 Fluence distributions and phase distributions of the FW and the TH at several typical propagation distances |
|
To make sure whether the FW and the TH are vortices during the co-filamentation, we plot the phase distributions of the two fields when the initial FW has symmetrical perturbation and peak power 31.3 GW, as shown in Fig. 3 (c) and 3(d). The initial phase distribution of the FW can be seen from the Fig. 1 (c). Because the initial topological charge of the FW mω equals 1, the change of phase in a circle is 2π, and the phase only depends on the azimuthal angle. When the FW vortex beam begins to self-focus and the intensity is not so high (z=1.0 m), the spiral distribution of the phase is kept. Because the intensity distribution relies on the radius for the FW, the phase modulation by Kerr effect results in that the phase distribution not only depends on the azimuthal angle but also depends on the radius. During this process, the FW keeps the characteristics of vortex. Correspondingly, for the TH, the spiral phase distribution is also observed at z=1.0 m. The change of the phase in a circle is 6π, three times that of the FW phase. It suggests that the topological charge of the TH m3ω equals 3. The conservation of the topological charge is in accordance with that in Ref. [21]. In the filamentation region (z=2.0 m), the phase distributions of the FW and TH have a slight change. Because the FW filaments intensity is much higher than that in other regions, the phase accumulation due to Kerr effect is much larger. The phase accumulation in the filaments region results in a distortion in the filamentation annulus. The spiral phase in the annulus is destroyed slightly. Correspondingly, the phase distribution of the TH is also distorted in the annulus. From Fig. 3 (c) and 3(d), we can also see that during the dispersion of the filaments, the most parts of the FW and TH keeps the spiral phase with a slight distortion (z=3.0 m and z=4.0 m). Therefore, during the co-filamentation, the most parts of the two fields keep the phase distribution of vortices. The fluence evolution and the phase distribution suggest that the topological charge of the TH equals 3, and both the FW and the TH keep the vortex characteristics in the filamentation regime.
The evolution of the two-color vortex is also investigated when the initial FW vortex beam has a higher power of 62.7 GW and symmetrical perturbation. In this case, the fluence and phase distributions of the FW and the TH are shown in Fig. 4.

|
Download:
|
|
The symmetrical perturbation is initially introduced into the FW vortex beam which has a peak power of 62.7 GW. Out of the black circle the phase distribution of TH is distorted in (d) at z=2.0 m. Fig. 4 Fluence distributions and phase distributions of the FW and the TH at several typical propagation distances |
|
During the co-propagation, the evolution of the TH also follows that of the FW. From Fig. 4 (a) and 4(b), we can see that for the FW and the TH, four filaments are formed at z=0.76 m. Correspondingly, the spiral phase distributions of the two fields are destroyed slightly in the annulus, as shown in Fig. 4 (c) and 4(d). Then, with the interaction of the four filaments, new filaments are generated. The filaments are distributed as a necklace. With the formation of more filaments, the spiral phase distributions are destroyed in most part, as shown in Fig. 4 (c) and 4(d) at z=1.0 m. After the termination of the filamentation, the annulus distributions of the intensity are distorted greatly (see Fig. 4 (a) and 4(b) z=2.0 m). The phase distributions in most parts of the two fields are also distorted. These results suggest that for the FW with symmetrical perturbation and much higher peak power, both the FW and the TH can maintain the annular intensity distribution of the vortex in the filamentation regime. But the phase distribution of the vortex cannot be maintained.
We also investigate the co-propagation of the FW and the generated TH when the initial FW vortex beam has an asymmetrical perturbation. The initial distribution of the perturbation is described by the Eq. (8), and the initial fluence distribution of the FW is shown in the Fig. 1 (b). Figure 5 (a) shows that for the FW with peak power of 31.3 GW, the evolutions of the peak intensity for both the FW and the TH are similar to those in the symmetrical perturbation condition. But the filament intensity is higher than that in the symmetrical perturbation condition, as shown in the Fig. 2 (a). Correspondingly, the evolutions of the energy and the conversion efficiency of the TH are also similar to those in the symmetrical perturbation condition. The maximal energy of TH is 1.4 μJ, and the maximal conversion efficiency is 0.14%, higher than those in the symmetrical perturbation condition, as shown in Fig. 5 (b) and Fig. 2 (c).

|
Download:
|
|
The asymmetrical perturbation is initially introduced into the FW vortex beam which has a peak power of 31.3 GW. Fig. 5 Peak intensities of the FW and the TH, and the energy and conversion efficiency of the TH as a function of propagation distance |
|
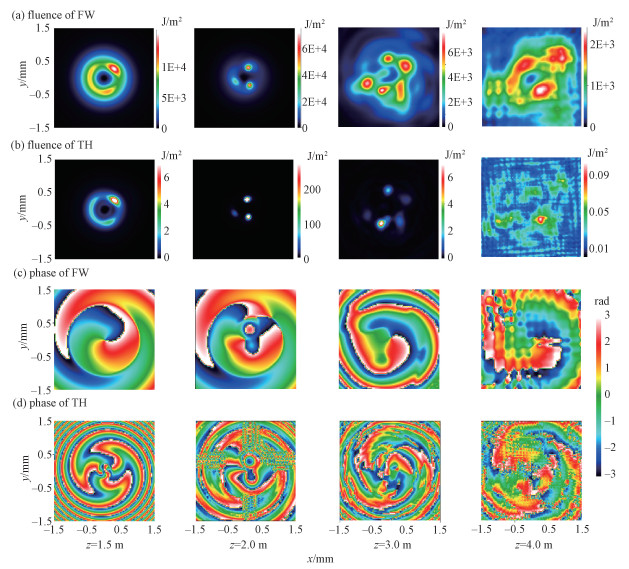
In this case, one hot spot is formed due to the self-focus of the asymmetrical perturbation at z=1.5 m, as shown in Fig. 6 (a). Then the multiple filaments are generated in the annulus at z=2.0 m. With the evolution of the multiple filaments, the intensity annulus is destroyed, as shown in Fig. 6 (a) at z=3.0 m and z=4.0 m. Figure 6 (b) shows that the evolution of the generated TH follows that of the FW. The annulus of TH is also destroyed with the generation of the multiple filaments. Therefore, the asymmetrical perturbation of the initial FW leads to the spatial breakdown of the two-color vortex. This is due to the asymmetrical energy replenishment during the filamentation, which is caused by the modulation instability[22]. The corresponding phase distributions of the FW and the TH are also plotted in Fig. 6 (c) and 6(d). At z=1.5 m, one spot is formed for the FW and the TH, and the intensities of the FW and the TH are lower. The phase accumulation of this spot is not large. Therefore, the phase distortion of the two fields is not obvious. The spiral phase is also observed for the two fields. After that, the filament intensity becomes higher and higher. With the formation of the multiple filaments, the phase accumulation of these filaments results in the obvious distortion in the phase distributions of the two fields. In this case, the spiral phase of the vortex for both fields is not observed. Therefore, the initial asymmetrical perturbation of the FW results in the damage of the two-color vortex, including the annular intensity distribution and the spiral phase.
|
Download:
|
|
The asymmetrical perturbation is initially introduced into the FW vortex beam which has a peak power of 31.3 GW. Fig. 6 Fluence distributions and phase distributions of the FW and the TH at several typical propagation distances |
|
In this paper, we have simulated the co-propagation of the femtosecond vortex beam and the generated TH vortex in air. The influences of the power and the perturbation distribution on the evolution of the two-color vortex have been investigated. It is shown that for the initial FW with symmetrical perturbation, the spatial annulus of the two-color vortex can be maintained in the filamentation regime. For the low peak power, the spiral phase in most parts of the FW and the TH can also be maintained. But with the increase of the initial peak power, the spiral phase of the two-color vortex is destroyed due to the phase accumulation of the multiple filaments. For the initial FW with asymmetrical perturbation, both the spatial annulus and the spiral phase of the two-color vortex are destroyed when multiple filaments are formed. This study is helpful to understand the nonlinear co-propagation of the two-color vortex and important for the potential applications.
| [1] |
Aközbek N, Iwasaki A, Becker A, et al. Third-harmonic generation and self-channeling in air using high-power femtosecond laser pulses[J]. Physical Review Letters, 2002, 89(14): 143901. DOI:10.1103/PhysRevLett.89.143901 |
| [2] |
Kasparian J, Rodriguez M, Méjean G, et al. White-light filaments for atmospheric analysis[J]. Science, 2003, 301(5629): 61-64. DOI:10.1126/science.1085020 |
| [3] |
Bergé L, Skupin S, Méjean G, et al. Supercontinuum emission and enhanced self-guiding of infrared femtosecond filaments sustained by third-harmonic generation in air[J]. Physical Review E, 2005, 71(1): 016602. DOI:10.1103/PhysRevE.71.016602 |
| [4] |
Kolesik M, Wright E M, Becker A, et al. Simulation of third-harmonic and supercontinuum generation for femtosecond pulses in air[J]. Applied Physics B: Lasers and Optics, 2006, 85(4): 531-538. DOI:10.1007/s00340-006-2415-7 |
| [5] |
Théberge F, Luo Q, Liu W, et al. Long-range third-harmonic generation in air using ultrashort intense laser pulses[J]. Applied Physics Letters, 2005, 87(8): 081108. DOI:10.1063/1.2033148 |
| [6] |
Xi T T, Lu X, Zhang J. Enhancement of third harmonic emission by interaction of two colored filament with droplet in air[J]. Optics Communications, 2009, 282(15): 3140-3143. DOI:10.1016/j.optcom.2009.04.038 |
| [7] |
Liu Y, Durand M, Houard A, et al. Efficient generation of third harmonic radiation in air filaments: a revisit[J]. Optics Communications, 2011, 284(19): 4706-4713. DOI:10.1016/j.optcom.2011.05.050 |
| [8] |
Feng L B, Lu X, Xi T T, et al. Numerical studies of third-harmonic generation in laser filament in air perturbed by plasma spot[J]. Physics of Plasmas, 2012, 19(7): 072305. DOI:10.1063/1.4737578 |
| [9] |
Ariunbold G O, Polynkin P, Moloney J V. Third and fifth harmonic generation by tightly focused femtosecond pulses at 22μm wavelength in air[J]. Optics Express, 2012, 20(2): 1662-1667. DOI:10.1364/OE.20.001662 |
| [10] |
Mao G L, Wu Y H, Singer K D. Third harmonic generation in self-focused filaments in liquids[J]. Optics Express, 2007, 15(8): 4857-4862. DOI:10.1364/OE.15.004857 |
| [11] |
O'Connor S P, Marble C B, Nodurft D T, et al. Filamentation in atmospheric air with tunable 1100~2400 nm near-infrared femtosecond laser source[J]. Scientific Reports, 2019, 9(1): 12049. DOI:10.1038/s41598-019-48542-1 |
| [12] |
Garejev N, Gražulevičiūtė I, Majus D, et al. Third- and fifth-harmonic generation in transparent solids with few-optical-cycle midinfrared pulses[J]. Physical Review A, 2014, 89(3): 033846. DOI:10.1103/PhysRevA.89.033846 |
| [13] |
Shipilo D E, Mokrousova D V, Panov N A, et al. Third-harmonic generation from regularized converging filaments[J]. Journal of the Optical Society of America B, 2019, 36(2): A66-A71. DOI:10.1364/JOSAB.36.000A66 |
| [14] |
Liu Z Y, Ding P J, Shi Y C, et al. Control of third harmonic generation by plasma grating generated by two noncollinear IR femtosecond filaments[J]. Optics Express, 2012, 20(8): 8837-8847. DOI:10.1364/OE.20.008837 |
| [15] |
Panagiotopoulos P, Papazoglou D G, Couairon A, et al. Sharply autofocused ring-Airy beams transforming into non-linear intense light bullets[J]. Nature Communications, 2013, 4: 2622. DOI:10.1038/ncomms3622 |
| [16] |
Porras M A, Ruiz-Jimenez C, Losada J C. Underlying conservation and stability laws in nonlinear propagation of axicon-generated Bessel beams[J]. Physical Review A, 2015, 92(6): 063826. DOI:10.1103/PhysRevA.92.063826 |
| [17] |
Polynkin P, Ament C, Moloney J V. Self-focusing of ultraintense femtosecond optical vortices in air[J]. Physical Review Letters, 2013, 111(2): 023901. DOI:10.1103/PhysRevLett.111.023901 |
| [18] |
Curtis J E, Koss B A, Grier D G. Dynamic holographic optical tweezers[J]. Optics Communications, 2002, 207(1-6): 169-175. DOI:10.1016/S0030-4018(02)01524-9 |
| [19] |
Tamburini F, Mari E, Sponselli A, et al. Encoding many channels on the same frequency through radio vorticity: first experimental test[J]. New Journal of Physics, 2012, 14(3): 033001. DOI:10.1088/1367-2630/14/3/033001 |
| [20] |
Swartzlander G A, Ford E L, Abdul-Malik R S, et al. Astronomical demonstration of an optical vortex coronagraph[J]. Optics Express, 2008, 16(14): 10200-10207. DOI:10.1364/OE.16.010200 |
| [21] |
Lin Y C, Nabekawa Y, Midorikawa K. Conical third-harmonic generation of optical vortex through ultrashort laser filamentation in air[J]. Optics Express, 2016, 24(13): 14857-14870. DOI:10.1364/OE.24.014857 |
| [22] |
Bespalov V I, Talanov V I. Filamentary structure of light beams in nonlinear liquids[J]. JETP Letters, 1996, 3(12): 307. |
 2021, Vol. 38
2021, Vol. 38 


