原子核物理与强子物理研究中一个重大的课题便是核子结构。核子是对质子和中子的统称，即构成原子核的粒子。最初人们认为质子自旋角动量的主要贡献来自组分夸克的自旋角动量以及它们之间的轨道角动量。然而电子与质子的散射实验发现，组分夸克的贡献仅占质子自旋的一小部分(约20%)。这一实验观测被称为“自旋危机(spin puzzle)”。现在质子自旋来源通常认为包括价夸克、海夸克和胶子的极化与轨道角动量贡献。质子内部结构的了解还远不足以解释其自旋的起源。这是因为测量质子内部各种成分的极化和轨道角动量十分困难。在粒子物理标准模型中，量子色动力学(quantum chromodynamics, QCD)是描述强相互作用的理论。在QCD因子化定理框架下，核子内部结构由部分子(夸克和胶子)分布函数所描述。横动量依赖(transverse momentum dependent, TMD)的部分子分布函数为描述部分子在横向动量空间的分布。轻子-核子半单举非弹性散射(semi-inclusive deep inelastic scattering, SIDIS)是实验测量TMD部分子分布函数的理想过程，其末态角分布结构为部分子分布函数与碎裂函数的卷积。实验上通过测量角分布结构抽取TMD函数和碎裂函数。

部分子碎裂到强子的产生过程无法精确计算，需要使用因子化方法引入夸克碎裂函数给出。Collins函数^[1-2]则是考虑了部分子自旋的碎裂函数。实验上测量的夸克碎裂函数将作为重要输入，理解强相互作用的非微扰性质。特别是极化夸克的碎裂函数测量，是深度非弹散射实验探测核子结构的关键输入。美国已经批准电子离子对撞机(electron ion collider，EIC)计划。中国原子核物理领域也正在推动中国电子离子对撞机计划(electron ion collider plan in China，EicC)。电子离子对撞机利用电子轰击极化质子靶，通过SIDIS研究质子的内部结构以及质子的自旋等问题。EicC实验要求Collins函数的测量能够达到2%的精度。实验上，HERMES实验通过测量Collins函数与部分子分布函数的耦合，观察到了Collins效应非零的证据^[3]，HERMES^[4]，COMPASS^[5]，JLab^[6]等一系列打靶实验都开展了进一步的相关测量，但是这些深度非弹实验都无法对Collins效应进行单独的抽取。另一方面，e⁺e^-对撞实验可以通过正负电子湮灭产生强子末态的过程(类时散射)，直接测量Collins函数，进而结合深度非弹实验抽取出TMD函数。Belle^[7-9]，BARBAR^[10]和BESⅢ^[11]等实验都给出了非零的Collins不对称度。但是Belle和BarBar都运行在高能区(Q²~100 GeV²)，而深度非弹的能区在Q²=2~50 GeV²。当前世界上仅有BESⅢ可以测量低能区Collins碎裂函数，更接近深度非弹的实验能标。超级陶粲装置(super tau-charm facility, STCF)设计能量在2~7 GeV，正好与EIC的设计能标2~50 GeV²相配。因此在STCF上开展Collins测量，一方面可以填补10~50 GeV²能区的测量空白，另一方面，其测量结果也可以作为EIC与EicC的输入，提高部分子分布函数测量的精度，并对理解自旋危机带来帮助。另外，由于目前世界上的SIDIS的K介子数据精度有限，因此大量的Collins测量对TMD的味道分离也有很大的帮助。

1 超级陶粲装置

北京正负电子对撞机(Beijing electron positron collider Ⅱ，BEPCⅡ)BESⅢ^[12]实验运行在陶-粲能区，是强相互作用理论从微扰到非微扰的过渡能区。为研究轻强子谱学、强子结构、陶轻子物理、粲强子物理、粲偶素以及新物理提供了独特的平台。北京谱仪实验将于5~8年内结束其历史使命，目前国内的粒子物理领域正在开展后BESⅢ时代的中国加速器粒子物理可能项目的预研。由于超级陶-粲装置是北京正负电子对撞机BESⅢ实验的自然延申，且覆盖更宽的能区，以及更为丰富的物理研究课题，被认为是后BESⅢ时代中国加速器粒子物理的重要选项之一。

物理分析使用的事例需要知道末态径迹的粒子种类信息，探测器一般通过粒子鉴别系统对带电径迹末态参数的计算以识别粒子种类。粒子鉴别是离线软件中的重要组成成分，对物理分析的结果有重要的影响。BESⅢ主要用漂移室的电离能量损失dE/dx，飞行时间计数器(time of flight, TOF)的飞行时间进行长寿命带电粒子的鉴别。然而这两种方式的粒子鉴别能力随粒子动量增长而下降^[13]。一方面，他们的鉴别效率随动量的增长而减小，动量大于1.4 GeV/c的粒子鉴别效率小于90%会导致高动量事例的减少。另一方面BESⅢ的研究表明动量小于700 MeV/c的粒子π→K误判率~1%，而动量高于1 GeV/c的粒子π→K误判率大于5%。一般认为dE/dx和TOF组成的粒子鉴别系统仅对动量 < 700 MeV/c的粒子区分能力较强，对高能粒子缺乏足够的分辨能力。因此，如果在STCF实验上采取契伦科夫探测器作为粒子鉴别系统的补充，将大幅提高高动量粒子的鉴别能力。

2 分析方法综述

Collins碎裂函数描述具有S_q和动量k的夸克q(部分子)碎裂到横动量为P_h⊥的强子过程。考虑到夸克自旋情形下，描述强子(h)的空间分布概率密度可以表达为

$ D_{\mathrm{h}, \mathrm{q} \uparrow}=D_{1}^{\mathrm{q}}\left(z, P_{\mathrm{h} \perp}^{2}\right)+H_{1}^{\perp \mathrm{q}}\left(z, P_{\mathrm{h} \perp}^{2}\right) \frac{\left(\hat{k} \times P_{\mathrm{h} \perp}\right) \cdot S_{\mathrm{q}}}{z M_{\mathrm{h}}}. $

(1)

式中：第1项含有非极化的碎裂函数D₁^q(z, P_h⊥²)，第2项为夸克自旋带来的影响。与Collins碎裂函数H₁^⊥q(z, P_h⊥²)和夸克的自旋方向有关，这里的z是强子带走的夸克能量分数。如果碎裂的夸克有确定的自旋方向，则末态强子在横动量空间的角度是不均匀的。在没有极化束流的情况下，可以利用e⁺e^-→γ^*→qq过程中夸克与反夸克自旋平行这一特性，同时观测2个Collins函数，也就是夸克和反夸克整体带来的效应。

可以将末态带电强子对分成电荷相同的组合(like-sign, π^±π^±)和电荷相反的组合(unlike-sign, π^±$\pi^{\pm}$)。对于碎裂函数描述的过程，如果碎裂产生的末态强子包含的价夸克包含碎裂的夸克类型(如u, d→π⁺; u, s→K⁺)，则对应的是favored碎裂函数，反之(u, d→π^-; u, s→K^-)则对应disfavored碎裂函数。因此，like-sign组合来自于1个favored和1个disfavored碎裂函数，而unlike-sign组合来自于2个favored碎裂函数或者2个disfavored碎裂函数贡献。采用Gottfried-Jackson定义^[14]，ϕ₀定义如图 1。考虑到Collins不对称，2ϕ₀的归一化分布可用R=1+A^U(L)cos2ϕ₀拟合，其中上标U(L)表示unlike-sign(like-sign)。但是因为探测器的接受度、效率不均匀问题，R的分布往往非常依赖于对于探测过程的模拟，带来很大的不确定性，不能精确地用于直接抽取Collins效应。

在我们的分析中，定义$R=\frac{N\left(2 \phi_{0}\right)}{\left\langle N_{0}\right\rangle}$，这里N(2ϕ₀)是每个2ϕ₀区间里介子对的产额，〈N₀〉是在每个2ϕ₀区间里2π(K)产额的平均值。分别构造unlike-sign，like-sign的归一化分布，称为R^U(2ϕ₀)，R^L(2ϕ₀)。将unlike-sign和like-sign的产额做比定义成DR(2ϕ₀)=R^U/R^L(DR：double ratio) 来抽取角不对称度。通过构造DR，电荷无关的来自探测器的效应被抵消了，依赖于电荷相关的不对称度得以显现。在一阶近似下DR的分布可以表示成

$ \operatorname{DR}\left(2 \phi_{0}\right)=\frac{R^{\mathrm{U}}}{R^{\mathrm{L}}}=1+A^{\mathrm{UL}} \cos \left(2 \phi_{0}\right). $

(2)

这里A^UL可以用来表示Collins不对称度。在模拟样本中并没有放入Collins效应，因此DR应该呈现平的分布。

为了研究Collins效应随π(K)粒子能量占束流能量分数z(z=E_π(K)/E_beam)的行为，将所有的强子对按照2条径迹的z₁, z₂的大小，分成不同的{z₁, z₂}区间。考虑每个区间的不同的统计量，将z₁(z₂)分成4个分划，[0.15, 0.2)，[0.2, 0.3)，[0.3, 0.5)和[0.5, 0.9]，对称的分组可以合成一组，如：z₁∈[0.2, 0.3), z₂∈[0.3, 0.5)与z₁∈[0.3, 0.5), z₂∈[0.2, 0.3)合并为一组。因此本来4×4的{z₁, z₂}可以简化为10个动量区间。{z₁, z₂}区间的定义见表 1。

3 模拟样本

考虑到大部分强子来自于e⁺e^-→qq，我们在质心能量为7 GeV利用产生子Lundarlw^[15]，大量模拟qq蒙特卡罗样本(Monte Carlo sample, MC)，亮度为2.5 fb^-1，用于Collins不对称度的敏感度研究。此外模拟了大量的QED本底过程，包含Bhabha事例(e⁺e^-→e⁺e^-)，e⁺e^-→γγ，μ⁺μ^-，e⁺e^-X等MC模拟样本。对于每种QED本底过程各自模拟了1 000 000个事例。

模拟样本的重建基于STCF项目组开发的快速重建包STCFastSimAlg。它可以读取样本中的末态粒子四动量信息，基于不同粒子的动量分辨、探测效率、粒子类型判断效率以及粒子误判几率等信息对末态粒子进行效率舍选和动量改变。舍选后的事例可以被当成假数据应用到STCF的预研工作中。作为初次预研，STCFastSimAlg采用BESⅢ实验的径迹重建以及粒子鉴别的效率曲线。由于分析的末态粒子是一对π(K)，粒子的K-π误鉴别将会对我们的分析带来很大影响。如前所述，传统的dE/dx和TOF的粒子鉴别系统只能很好地区分动量小于700 MeV/c的Kπ粒子，而对动量大于700 MeV/c的粒子dE/dx和TOF都缺乏足够的鉴别能力。而STCF的对撞质心系能量将会达到7 GeV，模拟的πK动量显示(参见图 2)，动量大于700 MeV/c的末态粒子将占用很大比例。因此高能区的K-π误鉴别将会对我们的信号带来污染。为了提高高动量下的粒子鉴别能力，STCF拟采用契伦科夫探测器作为粒子鉴别系统的补充，K-π误鉴别能力能够降低至1%以下。因此在分析中将K-π误鉴别水平设为1%。

4 事例选择

在B工厂，e⁺e^-→qq过程中的2个夸克携带有大量的能量。在接下来的强子化过程中会碎裂成2个背对背的喷注(jet)，通常定义冲度(Thrust，简称T)为末态径迹的动量在某一空间轴的投影：

$ T=\operatorname{Max}\left[\frac{\sum_{\mathrm{h}}\left|\boldsymbol{p}_{\mathrm{h}} \cdot \hat{\boldsymbol{n}}\right|}{\sum_{\mathrm{h}}\left|\boldsymbol{p}_{\mathrm{h}}\right|}\right]. $

(3)

其中：$\hat{\boldsymbol{n}}$是单位向量，p_h是质心系内强子动量，冲度轴是使得冲度值达到最大的方向。B工厂实验上，冲度轴可以认为是qq背对背的运动方向。冲度的取值范围为0.5~1，对于几乎各向同性的事例来讲，其冲度值接近0.5，对于背对背的两喷注事例，冲度值约等于1。B工厂要求T>0.8来排除胶子辐射e⁺e^-→qqg事例，因为这个过程不能保证q和q的量子关联。但是，由于STCF能区低于B工厂能量区，并没有明显的冲度轴，所以在预研中采用更贴近于BESⅢ的事例筛选条件选择可能的ππX和KKX事例。

4.1 好径迹的判选条件

径迹的极角|cosθ| < 0.93，即要求径迹在探测器接收度以内。径迹顶点和束流对撞顶点的距离在x-y平面上满足：d_r < 1 cm；径迹顶点和束流对撞点位置的距离在z方向满足|d_z| < 10 cm，即要求径迹来自于对撞顶点，以排除宇宙线或束流本底。

4.2 好光子选择条件

对于桶部光子(极角|cosθ| < 0.8)在电磁量能器沉积能量的E>25 MeV；对于端盖光子(0.86 < |cosθ| < 0.92) 的沉积能量E>50MeV。要求簇射的电子学时间：0≤t≤14(×50 ns)。

4.3 Kπ粒子鉴别

在模拟过程中，将K→π和π→K的误判率都设成1%。对于ππX(KKX)过程，要求事例中至少有3条好带电径迹，其中至少2条径迹被鉴别为π(K)。

4.4 其他的选择条件

为了排除QED本底过程，我们要求：1) 无鉴别为电子的径迹；2) 定义观测总能量E_vis为所有重建好带电径迹以及好光子的能量和，要求E_vis>1.5 GeV。目前在对Collins效应的理论估计中，都是考虑一对强子，分别来自于e⁺e^-产生的夸克以及反夸克的碎裂。对它们来自同一个夸克的情形不予考虑。在低能区，由于夸克携带的动量较小，不能够碎裂成喷注，难以区分一对强子是来自1个夸克还是来自于2个夸克的分别碎裂。因此在事例选择中我们要求2个强子的张角大于120°，尽量挑选背对背的强子，以避免来自于同一个夸克的碎裂。

5 本底成分研究

大部分强子来自于e⁺e^-→qq过程。利用信号样本和QED本底样本并使用dE/dx和TOF做粒子鉴别，经过样本估计QED本底中仅有τ⁺τ^-过程可以遗留下来，这个本底的来源是μ→π的误判，而在研究KKX时，由于μ→K的误判率较低，因此τ⁺τ^-对KKX过程的污染比例较少。

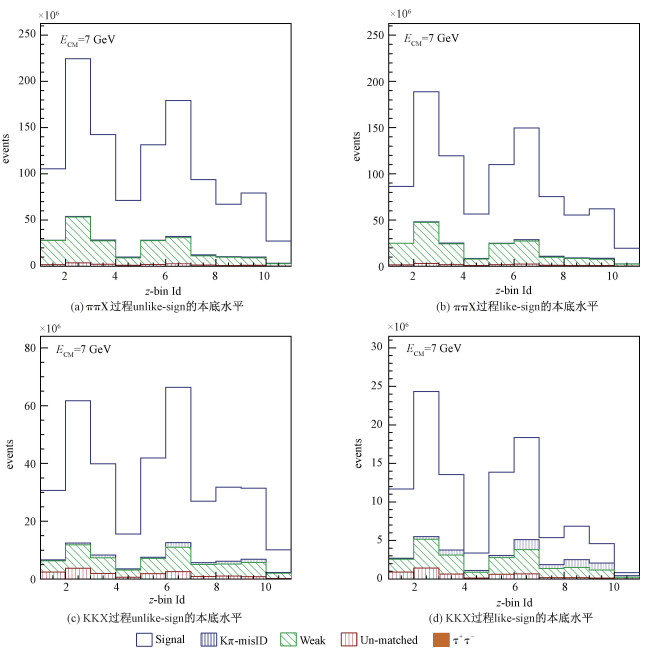
图 3为使用dE/dx和TOF做粒子鉴别的ππX和KKX过程的信号与本底分布。图 4为同样的样本，在STCFastSimAlg重建中控制π→K和K→π误判比例皆为1%，并忽略μ→π(K)误判。图 3和图 4中(a, b)代表ππX过程中{z₁，z₂}区间中不同成分的本底情况，(c, d)代表KKX过程中{z₁，z₂} 区间中不同成分的本底情况。亮度归一到1 ab^-1。橙色部分表示τ⁺τ^-本底，蓝色阴影为K-π误判本底，红色竖纹为假径迹本底，绿色斜纹为弱衰变本底。由于在STCFastSimAlg重建中控制了π→K和K→π误判比例皆为1%，并忽略μ→π(K)误判。所以图 4的τ⁺τ^-本底基本消失。

在e⁺e^-→qq过程中，只有一对π(K)都是来自于强衰变才可以认为是信号。在样本中，可以匹配重建粒子的四动量与样本真实动量值。如果重建粒子动量与样本真实动量夹角小于10°，可以认为这一条径迹是被探测器正确重建的，反之，则这一条径迹有可能是电子噪声所造成的假径迹。经过匹配的径迹，可以确定样本中对应真实的粒子类型以及这个粒子母粒子以判断是来自于强衰变还是弱衰变。如果其真实的粒子类型是π(K)，但重建的粒子类型是K(π)，那么这条径迹是被K-π误判的；因此对于qq样本里的的ππ(KK)组合存在以下几种本底：

1) 弱衰变本底：如果ππ(KK)组合中有1条是来自于弱衰变，这样的ππ(KK)组合认为是弱衰变本底。

2) K-π误鉴别本底：非弱衰变来源的π(K) 来自于K-π误鉴别，则这样的ππ(KK)组合认为是K-π误鉴别本底。

3) 假径迹本底：如果ππ(KK)组合中有1条是径迹-真值匹配失败的，这种本底认为是假径迹本底。

图 3显示出使用dE/dx和TOF做粒子鉴别时KKX过程中的本底比例比远高于ππX过程。这是由于在qq的末态粒子中，π粒子产额是K的10倍量级，因此KKX过程本底的主要来源是π→K误鉴别，并且动量越高，所受误鉴别本底的影响越大。由图 3(b)和3(c)所示，高动量区间事例50%以上来自于K-π误判，甚至like-sign的高动量区间K-π误判事例占到80%，这必然导致KKX过程事例绝大部分来自于πKX过程误混本底的贡献。因此，高鉴别能力的契伦科夫探测器是必须的。图 4控制了K-π误判比例，所带来的本底也被大大压低。

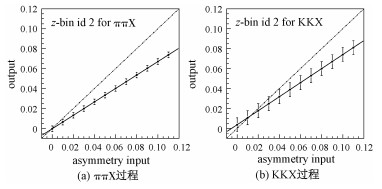
6 提取Collins效应

为了研究对于不同大小的Collins不对称度的测量精度，用舍选法将来自于强衰变的ππ(KK)的unlike-sign和like-sign组合分别按照1+A_input^U(L)cos2ϕ₀进行抽样。为方便起见，令unlike-sign组合的不对称度AU_input为0.000, 0.005, 0.010, …, 0.055，并且令A_input^L=-A_input^U。在一阶近似下相当于放入A_input^UL=A_input^U-A_input^L分别为0.00, 0.01, 0.02, …, 0.11。这里的A_input^UL称为研究测量值。将不同{z₁, z₂}区间里面的DR(2ϕ₀)分成20个区间，合理地考虑每个区间的统计误差，并用1+Acos(2ϕ₀)进行最小二乘拟合。其拟合结果A_output^UL对应不同输入值的测量输出值。在所有{z₁, z₂}区间中，由输出值和输入值所构成的二维点显示出明显的正相关趋势。图 5展示第2个{z₁, z₂}区间的ππX过程和KKX过程的输出值vs. 输入值的二维分布结果。带误差的黑点为输出值vs.输入值，虚线为y=x参考线，实线为拟合线。通过对每一个{z₁, z₂}区间用A_output^UL=b+kA_input^UL进行线性拟合，可以得到输出-输入线的截距与斜率，其物理意义在接下来的内容中会详细讨论。

7 结果讨论 7.1 对1 ab^-1数据的统计误差估计

利用2.5 fb^-1的7 GeV的qq模拟样本研究Collins效应的测量精度。作为初次预研，STCFastSimAlg采用BESⅢ实验上的径迹重建以及粒子鉴别的效率曲线，并将K-π误鉴别水平设为1%。由于ππX的截面高，其测量精度较高。取一个典型的假设A_input^UL=0.03，输出值A_output^UL在各{z₁, z₂}区间中最小的统计误差为2.8×10^-3，最大的统计误差是8.4×10^-3。在STCF 1 ab^-1的亮度条件下，其统计误差可以达到(1.4~4.2)×10^-4量级。

而KKX的截面较低，KKX的测量统计误差较大，同样取A_input^UL=0.03，输出值A_output^UL在各{z₁, z₂}区间中最小的统计误差为7×10^-3，最大的统计误差是39×10^-3。相应的在STCF 1 ab^-1的亮度条件下，其统计误差可以达到(3.5~20)×10^-4量级。

为了精确测量核子内的TMD分布函数，EicC将需要约2%的Collins输入精度。图 6展示不同动量区间1 ab^-1亮度的统计误差与EicC要求的2%的精度的比值随测量输入值的变化。可以看到1 ab^-1的亮度足以使得对Collins效应>0.07的测量精度优于2%。作为粒子鉴别系统的补充，使用契伦科夫探测器有利于提高高动量粒子鉴别的效率，测量精度会进一步提高。因此1 ab^-1的亮度完全满足需求。

7.2 A_output^UL和A_input^UL拟合线的截距

图 5显示出A_output^UL和A_input^UL存在线性关系，其截距为A_input^UL=0时对应的A_output^UL值。除个别动量区间以外截距是在误差内与0一致。这也与我们的预期相符——当测量的输入的Collins不对称为零时，输出的数值也应与零一致。因此我们认为A_output^UL=kA_input^UL。

7.3 A_output^UL和A_input^UL拟合线的斜率

上文所述，我们认为截距为0，因此拟合线化简为A_output^UL=kA_input^UL。理想情况下，输入值应与输出值相等，即斜率k=1，但是在ππX和KKX这2种情况下，所有的{z₁, z₂}动量区间里，k都小于1。为了合理地解释这个斜率，需要考虑到本底的贡献。

只有强相互作用产生的ππ(KK)对会存在有Collins效应，除了2个π(K)都来自强产生的信号，本底包含有弱衰变本底、K-π误判带来的本底和假径迹过程带来的本底。

假设这3种本底都会引入平本底，f^U(L)代表unlike-sign (like-sign)的平本底水平。DR可以这样构造：

$ \mathrm{DR}=\frac{R^{\mathrm{U}}}{R^{\mathrm{L}}}=\frac{f^{\mathrm{U}}+\left(1-f^{\mathrm{U}}\right)\left(1+A^{\mathrm{U}} \cos 2 \phi_{0}\right)}{f^{\mathrm{L}}+\left(1-f^{\mathrm{L}}\right)\left(1+A^{\mathrm{L}} \cos 2 \phi_{0}\right)} .. $

(4)

在一阶近似下

$ \mathrm{DR}=1+\left(1-f_{\mathrm{bk}}\right) A^{\mathrm{UL}} \cos \phi_{0}. $

(5)

其中: f_bk代表本底的比分，$f_{\mathrm{bk}} \approx \frac{1}{2}\left(f^{\mathrm{U}}+f^{\mathrm{L}}\right)$。用A_true^UL和A_meas^UL表示样本中真实存在的与测量到的不对称度，两者满足：

$ A_{\text {meas }}^{\mathrm{UL}}=\left(1-f_{\mathrm{bk}}\right) A_{\text {true }}^{\mathrm{UL}}. $

(6)

而这导致的结果就是A_output^ULvs.A_input^UL的拟合线斜率k=1-f_bk。

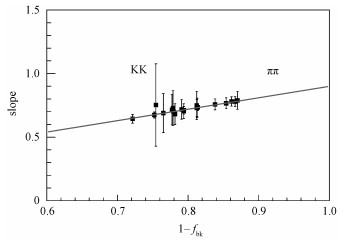
分别选取不同z区间的斜率，与每个z区间的底水平1-f_bk做二维点图，画入图 7。由于在ππX过程的本底较少，点集中在右边，KKX的本底较多，点集中在左边。用k_bk(1-f_bk)进行拟合。拟合结果k_bk=0.900±0.012，也即A_meas^UL=0.9(1-f_bk)A_true^UL。

如果考虑到KπX本底本身是具有Collins不对称度的本底，可以假设

$ \begin{gathered} R^{\mathrm{U}(\mathrm{L})}=f_{\text {flat }}+f_{\mathrm{K} \pi}\left(1+A_{\mathrm{K} \pi} \cos 2 \phi_{0}\right)+ \\ \left(1-f_{\text {flat }}-f_{\mathrm{K} \pi}\right) \times\left(1+A_{\pi \pi} \cos 2 \phi_{0}\right)= \\ 1+\left[f_{\mathrm{K} \pi} A_{\mathrm{K} \pi}+\left(1-f_{\text {flat }}-f_{\text {К\pi }}\right) A_{\pi \pi}\right] \cos 2 \phi_{0}, \end{gathered} $

(7)

$ A_{\text {meas }}^{\pi \pi}=\left(1-f_{\text {flat }}-f_{\text {К\pi }}\right) A_{\text {true }}^{\pi \pi}+f_{\text {K } \pi} A_{\text {true }}^{\text {K } \pi} .. $

(8)

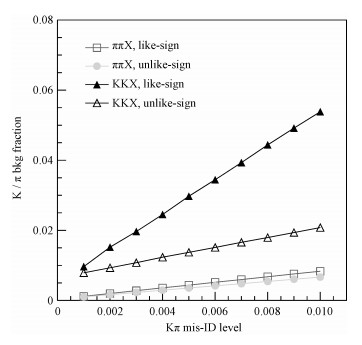
其中：f_flat主要由弱衰变本底贡献，其大小范围为(0.12~0.25)。由K-π误鉴别贡献导致的系统误差有f_KπA_true^ππ和f_KπA_true^Kπ。因此提高K-π的分辨能力能够大大压制f_Kπ从而减小系统误差。手动设置K-π误鉴别比例为0.001到0.01，由K-π误鉴别贡献的平均本底水平f_Kπ见图 8。在K-π误判在1%的水平下，KKX过程中like-sign的K-π误鉴别本底水平能达到近6%，甚至在个别高动量区间内，按照$f_{\mathrm{K} \pi}=\frac{1}{2}\left(f_{\mathrm{K} \pi}^{\mathrm{U}}+f_{\mathrm{K} \pi}^{\mathrm{L}}\right)$计算unlike-sign和like-sign综合的f_Kπ=15%，平均的f_Kπ也有4%。按照到A_true^ππ，A_true^KK和A_true^Kπ的大小相当来做一个简单的估计，f_flat将会导致Collins测量的绝对值12%~25%的偏小，因此测量中需确定平本底比例以修正结果。K-π误鉴别导致的f_Kπ在KKX过程的本底水平为4%，并且在个别高动量区间可能达到15%。这要求探测器在设计时选择合适的PID系统减小K-π误鉴别水平。同时KKX过程更容易受到KπX过程的Collins不对称度污染，因此提高KπX的Collins测量精度也是必要的控制误差手段。

8 结论

预研中的超级陶-粲装置，对撞质心系能量将覆盖2~7 GeV，是测量Collins效应的理想平台。由于其覆盖能区与EicC和EIC的能区符合，相关测量不仅会填补这个能区Collins测量的空白，也会极大地推动部分子分布函数的测量精度。同时也可以提供KKX的测量帮助理解TMD函数的味道分离。我们预计在7 GeV取数1 ab^-1，在这个亮度下，拟使用契伦科夫探测器，在其效率不低于BESⅢ的粒子鉴别效率时，预计ππX的Collins测量精度会达到(1.4~4.2)×10^-4量级，而KKX的精度会达到(3.5~20)×10^-4量级，在Collins效应>0.07的条件下完全可以满足EicC上2%的精度要求。输入输出检查显示由于假径迹与弱相互作用本底的存在，在2ϕ₀谱上可能会引入平本底，导致我们最终的测量结果绝对值偏小。平本底水平一般在12%~25%量级，会对测量结果的绝对值带来12%~25%的减小。此外，本研究对高能区的粒子鉴别提出了要求。模拟显示，高能区的K-π误判会显著影响相关测量。特别是使用dE/dx和TOF作为粒子鉴别系统时，KKX过程的高动量区间受K-π误判所导致的本底事例高达50%以上，因此提高粒子鉴别系统能力是必要的。STCF拟采用契伦科夫探测器作为粒子鉴别系统的补充，将K-π误鉴别水平降至1%以下。在STCF快速模拟重建软件STCFastSimAlg中，控制π→K和K→π误判比例皆为1%的条件下，KKX过程中的K-π误混比例降低至4%，这对KKX过程的分析造成4%的误差。因此本研究强烈建议在STCF实验上采用契伦科夫光探测技术，提高高动量的K-π鉴别。