2. 中国科学院大学, 北京 100049;
3. 三维及纳米集成电路设计自动化技术北京市重点实验室, 北京 100029
2. University of Chinese Academy of Science, Beijing 100049, China;
3. Beijing Key Laboratory of Three-dimensional and Nanometer Integrated Circuit Design Automation Technology, Beijing 100029, China
随着芯片电路的规模和工作时钟频率的提高,功耗大成为集成电路设计必须面对和解决的问题,且时钟树功耗所占比重也越来越大,因此如何降低时钟树功耗是近年来芯片设计领域研究的热点。文献[1]采用缓冲器与反相器相结合的方法,实现了功耗的降低,但并未具体研究反相器(inverter)与缓冲器(buffer)应该如何选择。文献[2]通过直接设置功耗优化指令来降低时钟树功耗。文献[3]通过采用9种不同的参数约束条件得到功耗与时序的折中方案。文献[4]采用时钟缓冲器优化技术,删除冗余缓冲器,进而实现时钟树功耗的降低。目前针对如何更好地选择驱动器去降低功耗尚未有相关研究。本文将基于时钟树设计中的扇出数与驱动器选择策略这2个变量,对时钟树进行低功耗研究。
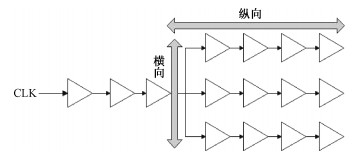
1 时钟树功耗分析图 1为时钟树的结构图,时钟树是由时钟驱动器连接而成的树形结构。时钟树分为纵向和横向分布,由图 1可以看出,横向分布由时钟树的扇出数决定。在电路时钟汇入点分布确定的前提下,当扇出数增大时,其横向分布增大,纵向分布减小[5],驱动时钟树横向分布和纵向分布的驱动器的数量就随之发生变化,进而引起功耗的变化。也即,时钟树的扇出数会影响时钟树的功耗,选择合理的扇出数会降低时钟树的功耗。
|
Download:
|
| 图 1 时钟树结构图 Fig. 1 Clock tree structure diagram | |
另一方面,驱动器是时钟树功耗的主要贡献者,同时其输入电容又影响着时钟树的负载电容。于是,选择合适的驱动器也会降低时钟树功耗。本文中,驱动器为标准单元库中的反相器和缓冲器。
由上可知,时钟树的扇出数和驱动器的选择策略都直接影响时钟树的功耗,于是,本文将结合时钟树的扇出数与驱动器选择策略这2个变量,对时钟树的功耗优化进行分析和研究。
2 时钟树功耗优化设计 2.1 面向低功耗的驱动器选择策略标准单元库中驱动器的驱动能力和功耗的关系主要表现在以下3个参数,即面积S、输入电容Cin以及最大输出电容Cout。驱动器的面积(尺寸)越大,其驱动能力越强,可以驱动的最大输出电容越大,但其自身功耗和输入电容形成的负载对功耗的影响也越大。
时钟树综合的目的就是形成驱动时钟信号的驱动器网络,将具有合适驱动能力的时钟信号按时序要求传递到各个不同负载的时钟汇入点,在此基础上同时降低钟树功耗是有相当难度的。为满足时钟树时序要求且功耗最小化,本文结合描述驱动器的驱动能力和功耗关系的3个参数,以选择标准单元库中全部反相器/缓冲器的驱动器选择策略为参考策略,同时提出如下3种新的驱动器选择策略以期获得最优策略:
1) 策略1:电容比值法
| $ f_1=\max \left(\alpha_1, \alpha_2, \cdots\right) \cdot \alpha_i(i=1, 2, 3 \cdots)=\frac{C_{\mathrm{out}, i}}{C_{\mathrm{in}, i}} . $ | (1) |
如式(1)所示,f1为策略1的驱动器选择函数,max()表示选取最大值,采用上述3个参数中最大输出电容与输入电容的比值进行选取,选取比值较大的驱动器组合。α越大,意味着驱动能力强且作为负载时其电容小、功耗低。电容比值法综合考虑了驱动能力与功耗:驱动能力是时钟树的正向指标,功耗是时钟树的负向指标,因此根据α来进行选择具有可行性;
2) 策略2:平均值法
| $ f_2=\min \left(\left|C_{\text {out }}-\operatorname{avg}\left(C_{\text {out }}\right)\right|\right). $ | (2) |
如式(2)所示,f2为策略2的驱动器选择函数,avg()表示产生平均值,采用数学方法中的平均值法,即同时考虑驱动和功耗的情况下,采取折中原则,选择输出电容靠近于平均输出电容的驱动器;
3) 策略3:去除极端值法
| $ f_3=1-\{\max (S), \min (S)\} . $ | (3) |
如式(3)所示,f3为策略3的驱动器选择函数,max()表示选取面积最大值,min()表示选取面积最小值。去除极端值法是一般数学计算中常用的数据处理方法。也即不选择驱动能力过小、面积过大的驱动器。
2.2 不同时钟树对时序的影响针对某个具体的电路,基于不同驱动器选择策略,时钟树综合所产生的时钟树规模是不同的,时钟树规模的减少会使得时钟树对时钟偏差的调控变得粗糙[6],对时序会有不利的影响;同时使用不同的驱动器,在一定的时序约束下,时钟树综合所产生的时钟树的时钟偏差也有所差异。下边两式为建立时间和保持时间的时序检查公式
| $ T>t_{\text {clk-q }}+t_{\text {logic }}+t_{\text {setup }}+t_{\text {skew1 }} . $ | (4) |
| $ t_{\text {clk-q }}+t_{\text {logic }}>t_{\text {hold }}+t_{\text {skew} 2}. $ | (5) |
其中:tclk-q为寄存器的传输时间、tlogic为逻辑电路的延时、tsetup为寄存器的建立时间、thold为寄存器的保持时间。时钟偏差对建立时间和保持时间时序的检查至关重要[7-10]。结合图 2,时钟偏差tskew1为时钟信号到达FF1时钟端口的时间与到达FF2时钟端口的时间之差,时钟偏差tskew2为时钟信号到达FF2时钟端口的时间与到达FF1时钟端口的时间之差。由此可知,时钟偏差越大,对建立时间和保持时间的检查都是不利的。

|
Download:
|
| 图 2 时序分析模型 Fig. 2 Timing analysis model | |
由上可知,不同的时钟树选择策略对功耗和时序会产生不同的影响,因此,为了实现功耗和时序的综合优化,本文以最小化时钟树功耗和时钟偏差的乘积为目标。设功耗值和时钟偏差值是2个高斯分布的独立变量,考虑优化的精确度,本文以2个变量方差相等的原则进行优化,也即,采用如下式的优值因子W进行选择优化
| $ W=P^3 \times \text { skew. } $ | (6) |
其中:P为时钟树功耗,单位为mW;skew为时钟偏差,单位为ps。
优值因子W为功耗与时钟偏差的乘积公式。在某一具体情况下,W获得最小值,就认为是优值因子W的最优值。
3 实验结果和分析下面,以优值因子W为评价标准,对第2节提出的4种驱动器选择策略进行对比实验,并对比分析扇出数与驱动器选择策略对时钟树设计的影响。
基于130 nm工艺设计的专用信号处理器芯片,用后端设计软件IC Compiler下进行实验验证,验证中所使用的工艺角是tt(1.25 V/25 ℃)、ff(1.32 V/-40 ℃)、ss(1.08 V/125 ℃)。所用工艺的标准单元库中的缓冲器和反相器的面积S、输入电容Cin以及最大输出电容Cout的典型参数值如表 1所示。
|
|
表 1 标准单元库中缓冲器/反相器参数值 Table 1 Parameter value of buffer/inverter in standard cell library |
针对本文中电路的规模,同时考虑到扇出数设置过大会导致时钟树上驱动器数量较少,影响到时钟树的转换时间(transition),造成时序违例,所以,初步设置时钟树扇出数为40、60、80和100用于扇出数的优化选择。
相比于驱动器选择参考策略,本文提出的3种驱动器选择策略需要从表 1中按各自的规则选择出反相器/缓冲器的组合。从表 1可知,缓冲器共有8种类型、反相器共有9种类型。为更好地与驱动器选择参考策略进行比较,设本文提出的3种驱动器选择策略分别选择反相器和缓冲器的个数为J个和K个,这里,J和K分别取3、4、5、6中的任一个数。也即,在某个驱动器选择策略下,基于不同扇出数,采用的反相器/缓冲器用Q(JK)表示,其中J代表该策略中反相器的个数、K代表该策略中缓冲器的个数。
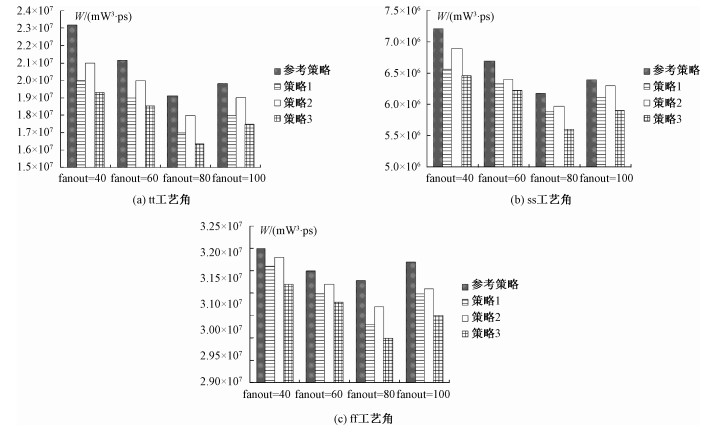
实验结果表明,在tt工艺角下,4种驱动器选择策略在不同扇出数情况下的W值如图 3(a)所示。从图 3(a)中可以看出,不同扇出下,本文提出的3种新的驱动器选择策略均比驱动选择参考策略要好;4种驱动选择策略的最优扇出数均为80;在最优扇出数为80情况下,除去驱动器选择参考策略是选择全部的反相器/缓冲器外,本文提出的3种驱动器选择策略的最优驱动器组合分别为Q(55)、Q(56)和Q(63)组合,具体如表 2所示。同理,在ss和ff工艺角下,4种驱动器选择策略在不同扇出数情况下的W值如图 3(b)、3(c)所示。从图 3(b)、3(c)可知,除W优值因子的绝对值有差异外,其他结论与tt工艺角下的结论相同。
|
Download:
|
| 图 3 不同工艺角下实验结果对比图 Fig. 3 Comparison chart of experimental results under different process corner | |
|
|
表 2 本文提出的3种驱动器选择策略的最优驱动器选择 Table 2 The optimal drive selection tof the three drive selection strategies proposed in this article |
由上可知,基于W优值因子,本文提出的3种驱动器选择策略要优于参考策略;时钟树的最优扇出数与驱动器选择策略相关性不大,本文中的最优扇出数为80;最优驱动器选择策略为选择策略3,且与驱动器选择参考策略相比,tt、ss和ff工艺角下的功耗分别降低5.82%、5.77%和6.10%。
由以上数据分析,从时钟树设计方法学的角度讲,可以得到一种新的低功耗时钟树设计方法:首先,基于任一驱动器选择策略,利用优值因子W选择出最优扇出数;然后,在选择出的最优扇出数下,采用本文提出的驱动器选择策略3(去除极端值法)选取驱动器,就可以设计出功耗低、时序优的时钟树。
4 结束语以扇出数与驱动器选择策略这2个变量,对时钟树功耗进行优化。以全部反相器/缓冲器的驱动器选择策略作为参考策略,同时提出电容比值法、平均值法和去除极端值法的驱动器选择策略。实验结果表明,本文提出的3种驱动器选择策略均比参考策略要好;最优扇出数与驱动器选择策略相关性不大。最后,总结出一种基于优值因子的低功耗时钟树设计方法。
| [1] |
潘静, 吴武臣, 侯立刚, 等. ASIC物理设计中的时钟树综合优化研究[J]. 微电子学, 2011, 41(6): 872-875. DOI: CNKI:SUN:MINI.0.2011-06-022.
|
| [2] |
杨兵, 张玲, 魏敬和, 等. ULSI后端设计低功耗技术研究[J]. 微电子学, 2014, 44(1): 10-13. DOI: CNKI:SUN:MINI.0.2014-01-003.
|
| [3] |
常晓夏, 潘亮, 李勇. 射频识别芯片设计中时钟树功耗的优化与实现[J]. 中国集成电路, 2011, 20(9): 36-39, 68. Doi:10.3969/j.issn.1681-5289.2011.09.051 |
| [4] |
戈喆, 付娟, 王沛东, 等. 低功耗时钟树的结构分析和缓冲器优化[J]. 中国集成电路, 2018, 27(12): 44-48. Doi:10.3969/j.issn.1681-5289.2017.09.006 |
| [5] |
王成龙, 张万荣, 万培元, 等. 一种UHF RFID标签低功耗物理设计与实现[J]. 固体电子学研究与进展, 2015, 35(3): 253-258. DOI: CNKI:SUN:GTD2.0.2015-03-009.
|
| [6] |
王延升, 刘雷波. SoC设计中的时钟低功耗技术[J]. 计算机工程, 2009, 35(24): 257-258, 261. Doi:10.3969/j.issn.1000-3428.2009.24.086 |
| [7] |
Joo D, Kim T. Managing clock skews in clock trees with local clock skew requirements using adjustable delay buffers[C]//2015 International SoC Design Conference (ISOCC). November 2-5, 2015, Gyeongju, Korea (South). IEEE, 2016: 137-138. DOI: 10.1109/ISOCC.2015.7401696.
|
| [8] |
Chakrabarti P. Clock tree skew minimization with structured routing[C]//2012 25th International Conference on VLSI Design. January 7-11, 2012, Hyderabad, India. IEEE, 2012: 233-237. DOI: 10.1109/VLSID.2012.76.
|
| [9] |
Ravi S, Trehan S, Jain M, et al. High performance clock path elements for clock skew reduction[C]//2019 2nd International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT). July 5-6, 2019, Kannur, India. IEEE, 2020: 1663-1670. DOI: 10.1109/ICICICT46008.2019.8993375.
|
| [10] |
罗恰嗣, 郭立, 周云超, 等. 一种EPC Gen2 RFID标签时钟校准方法[J]. 中国科学院研究生院学报, 2009, 26(6): 846-849. Doi:10.7523/j.issn.2095-6134-2009.6.017 |
 2023, Vol. 40
2023, Vol. 40 


