2. 中国科学院大学, 北京 100049;
3. 上海科技大学, 上海 201210
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. ShanghaiTech University, Shanghai 201210, China
卫星通信系统是未来全球通信系统的重要组成部分之一[1],其中低轨道(low earth orbit, LEO)卫星网络具有覆盖广、时延低和部署灵活等优势[2],将为全球提供低成本的商业通信服务。尤其在基础设施不完善、人口密度小的偏远地区,LEO卫星网络具有非常大的应用前景和发展潜力[3]。近年来,许多商业公司开始研究和部署大型LEO卫星网络为全球提供通信服务,代表性的网络有Starlink、OneWeb和天地一体化空间信息网络等[4]。
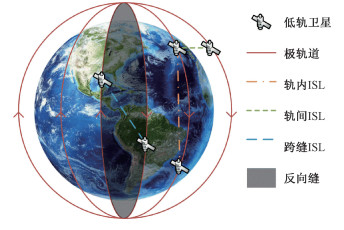
目前主流LEO卫星网络多数采用Walker星座,卫星之间通过星间链路(inter-satellite link, ISL)进行连接。按照部署轨道可将星座分为Walker倾斜轨道星座和Walker极轨道星座。对于Walker极轨道星座,由于第1轨道和最后1个轨道的卫星运行方向相反,将形成一个绕地心360°的反向缝。图 1给出了Walker极轨道星座反向缝示意图,圆形的极轨道导致反向缝左侧的卫星由南向北运行,右侧的卫星由北向南运行。
|
Download:
|
| 图 1 Walker极轨道星座反向缝 Fig. 1 Cross seam of Walker polar orbit constellation | |
反向缝两侧的卫星运行方向相反,可视时间短,需要针对性地设计建链策略。文献[5]分析得出,如果反向缝两侧的卫星之间不建链,将会极大增加网络的传输时延。文献[6-7]针对极轨道星座的反向缝问题,分别提出基于IP的路由最小化算法和数据包路由算法,降低传输时延。文献[8]提出一种跨轨道建链策略,通过减少路由跳数降低传输时延,但是会带来传输距离远、链路衰减严重等问题。这些研究工作无法从根本上解决反向缝不建链带来的传输时延问题。传统的波束固定指向天线无法直接用于反向缝建链,部分学者指出可以使用具有快速摆动和跟踪能力的新型空间微波或激光天线,实现反向缝建链。文献[9]提出一种基于射频天线的反向缝建链模型,简化了跨缝建链过程。在此基础上,文献[10]设计一种用于反向缝跟踪与传输的双转盘跨缝天线系统,实现了反向缝建链。
综上所述,通过合理设计能够在技术上实现反向缝建链。但已有文献大多通过优化同轨或者同向异轨建链策略降低传输时延,没有从根本上解决反向缝问题。针对极轨道LEO卫星网络的反向缝建链,本文提出一种星形交叉循环建链策略(star cross looping link-building strategy, SCLBS),通过在反向缝间智能建链,系统性地降低传输时延。首先参考卫星的允许建链距离,将反向缝处的可建链区划分为多个交叉建链区,然后在交叉建链区内星形建链,最后通过改变允许建链距离,在跨缝ISL的持续时间和数量之间进行权衡。通过优化网络容量,找到最优允许建链距离和参考纬度集合。最后利用参考纬度集合和卫星的星历数据,实现反向缝智能建链,降低系统的传输时延。本文使用自相关播报系统(automatic dependent surveillance broadcast, ADS-B)和自动识别系统(automatic identification system, AIS)实时采集的飞机与船舶数据,构建不同业务场景的用户数据分布模型,并且基于该模型对SCLBS进行仿真。结果表明,与基于最近卫星准则的建链策略[11]、基于最长可视时间准则的建链策略[12]和不跨缝建链策略[13]相比,SCLBS可以降低30%~60%的传输时延,改善反向缝附近的传输环境,明显减少全网卫星节点对之间的路由跳数。
1 系统模型与问题描述本节介绍极轨道LEO卫星网络的星座模型和业务模型,通过对研究问题进行建模,详细描述反向缝建链问题。
1.1 星座模型极轨道LEO卫星网络由多个经过极点的圆形轨道组成,每个轨道上运行着多个卫星。如图 1所示,2个相邻卫星之间存在3种ISL类型,分别是轨内ISL、轨间ISL和穿过反向缝的跨缝ISL[14]。轨内ISL始终保持不变,轨间ISL在极地之外的地区也比较稳定,怎样合理地在反向缝两侧的卫星之间建立稳定的跨缝ISL是本文研究的重点。
本文的星座模型假设每个卫星最多与4个相邻卫星建立ISL,对于反向缝两侧的卫星来说,包括2个轨内ISL、1个轨间ISL和1个跨缝ISL。将极轨道LEO卫星网络建模为无向图G=(S, L),其中S表示卫星集合,L表示ISL集合。因为传输距离和可视时间等因素的限制,只有形成反向缝的2条轨道上的卫星之间可以跨缝通信,这些卫星被称为可通信邻星,其他轨道的卫星需要通过可通信邻星转发才能实现跨缝通信。由于轨间ISL和跨缝ISL的周期性通断,LEO卫星网络拓扑会周期性地发生变化。本文将连续时间划分为一系列离散时隙,充分考虑各时隙之间网络拓扑的连续性。
1.2 业务模型考虑到LEO卫星网络的主要应用范围,使用ADS-B和AIS实时采集的数据建立全球用户数据分布模型。其中ADS-B由本单位的STU-2C立方星搭载,对全球空中交通信息进行采集;AIS由本单位的STU-2B立方星搭载,对全球海上交通信息进行采集[15]。
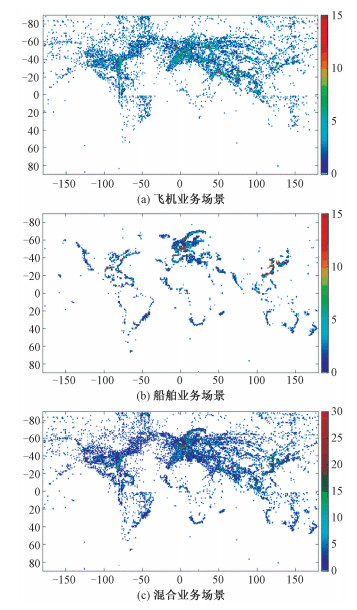
根据ADS-B和AIS实时采集的数据,分别建立不同业务场景下一个月内的数据分布,如图 2所示,包括飞机业务场景、船舶业务场景和混合业务场景3种。
|
Download:
|
| 图 2 不同业务场景下的用户数据分布 Fig. 2 User data distribution in different business scenarios | |
从图中可以看出,用户数据在全球范围内呈不均匀分布。飞机不受大陆和海洋的限制,数据分布比较随机。受到地形限制,船舶主要集中在港口和航海线附近,数据分布比较固定[15]。将两者相结合可以得到混合业务场景的用户数据分布。本文将根据3种业务场景的用户数据分布,随机确定进行跨缝通信的卫星对,对比不同建链策略的传输时延。
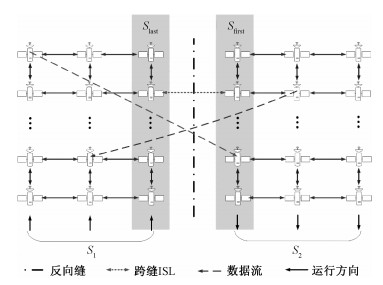
1.3 问题描述如图 3所示,反向缝两侧的卫星集合分别记为S1和S2,第1轨道和最后1个轨道内的卫星集合记为Sfirst和Slast。本文研究的重点是在同时考虑卫星运行周期和网络拓扑连续性的情况下,如何对Sfirst和Slast的卫星建立跨缝ISL,使得S1和S2之间进行数据传输的总传输时延最小。
|
Download:
|
| 图 3 卫星集合和数据流 Fig. 3 Satellite collection and data flow | |
2个卫星之间可以建立ISL的条件是它们之间的星间距离不能超过最远可视距离dmax,节点i在时刻t的可建链集表示为
| $N_i(t)=\left\{j \mid d_{i j}(t) \leqslant d_{\max }\right\}, $ | (1) |
其中dij(t)表示从节点i到节点j的距离。
令K表示S1和S2之间的数据流集合,Dk表示数据流k的传输时延,本文研究的优化问题可以表示为
| $\begin{aligned} & \qquad \min \sum\limits_{k \in K} D_k, \\ & \text { s. t. C1: } \sum\limits_j B_{j i}(t) \leqslant \sum\limits_{j^{\prime}} B_{i j^{\prime}}(t), i \neq j \neq j^{\prime}, \\ & \ \ \ \ \mathrm{C} 2: t_{i j^{\prime}}^{\mathrm{s}} \geqslant t_{i j}^{\mathrm{e}}+\Delta \tau, \\ & \ \ \ \ \mathrm{C} 3: l_{i j}^{\prime}(t)=l_{j i}^{\prime}(t), \\ & \ \ \ \ \mathrm{C} 4: \sum_j l_{i j}^{\prime}(t)=1, i \in S_{\mathrm{first}}, j \in S_{\mathrm{last}}, \end{aligned}$ | (2) |
其中:C1表示流量守恒约束条件,除转发的数据以外,节点本身也有需要传输的数据,在某个时刻流出节点的流量大于等于流入节点的流量。j表示向节点i传输数据的前向节点,j′表示从节点i接收数据的后向节点,Bji(t)表示时刻t从节点j到节点i的占用带宽。C2表示链路建立的时序约束条件,卫星在切换到下一条ISL的开始时间晚于上一条ISL的结束时间。lij表示节点i到节点j的ISL,tijs表示lij的开始时间,tije表示lij的结束时间。Δτ表示卫星从lij切换到lij′的时间开销,表示为
| $\Delta \tau=\tau_\theta+\tau_{\mathrm{t}}+\tau_{\mathrm{p}},$ | (3) |
其中:τθ是偏转时延,与2条链路的夹角θ有关,τt是跟踪时延,τp是准备时延,这2项在每次切换时都是固定的。约束条件C3表示链路的可视性是双向的,l′ij(t)表示时刻t的链路状态,l′ij(t)为1代表lij可以通信,为0代表lij不可通信。C4表示卫星在同一时刻只能建立1条跨缝ISL。
上述问题是一个近似NP的多变量混合非线性整数规划问题[14, 16],直接求解的复杂度极高,无法应用在计算能力有限的卫星载荷上。下一节将提出一种循环式的建链策略,快速求解公式(2)的优化问题。
2 算法设计针对极轨道LEO卫星网络的反向缝建链问题,将设计一种高效的建链策略。首先对研究问题的2个主要难点进行分析,然后详细介绍SCLBS建链策略。
2.1 问题分析本文的重点是研究高效可行的反向缝建链策略,通过在反向缝处选择部分卫星建立跨缝ISL,实现跨缝通信的同时最小化网络的传输时延。由于低轨卫星一直处于高速运动的状态,反向缝两侧运行方向相反的卫星之间可视时间短,可用的传输窗口有限。因此,在设计极轨道反向缝的建链算法时,面临着以下2个关键挑战:
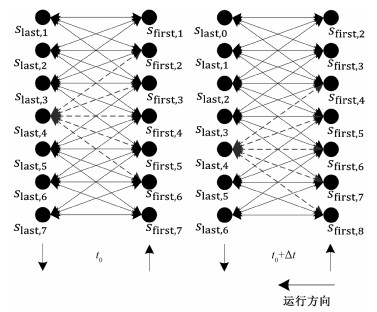
1) 相邻卫星的可建链卫星集合之间存在交集。如图 4所示,在时刻t0卫星slast, 4同时存在于sfirst, 2、sfirst, 3、sfirst, 4、sfirst, 5和sfirst, 6的可建链集中。在这种多星对多星的情况下,如何建立跨缝ISL,在任意时刻都能最大限度地利用跨缝ISL进行数据传输,并且避免卫星之间发生冲突,这是研究难点之一。
|
Download:
|
| 图 4 可建链集的变化情况 Fig. 4 Changes in the buildable link set | |
2) 反向缝处的星间链路切换频繁。因为反向缝两侧的卫星运行方向相反,相对速度变为运行速度的2倍,所以卫星可建链集的变化明显,导致跨缝ISL无法像轨内ISL与轨间ISL一样长时间保持稳定。同样如图 4所示,假设2个相邻时隙之间的时间间隔为Δt,从时刻t0变到时刻t0+Δt,slast, 4的可建链集减少了sfirst, 2和sfirst, 3,增加了sfirst, 7和sfirst, 8。每次切换链路的时间开销为Δτ,它与2个新旧链路之间的夹角有关。在这种情况下,如何从整体最小化切换带来的时间开销,是另一个重要的研究问题。
2.2 算法描述基于上述研究问题和难点,提出一种高效稳定的星形交叉循环建链策略SCLBS,其思路是首先根据允许建链距离将可建链区划分为多个交叉建链区,然后在每个交叉建链区内按照星形结构建链,最后通过最大化网络容量选择出最优允许建链距离和交叉建链区参考纬度集合,实现反向缝的智能建链。下面详细介绍每个步骤如何实现。
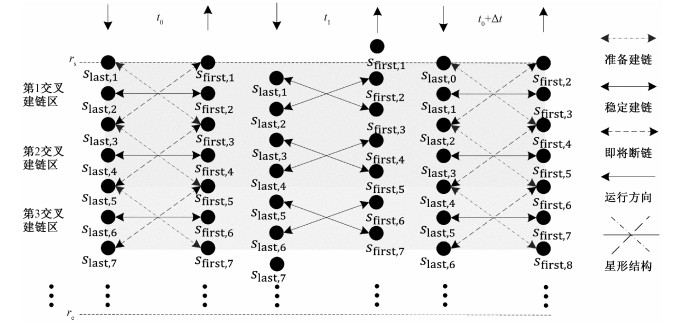
因为极轨道星座的轨道交点靠近极点,在极点附近地区卫星之间的相对位置变化过快,终端难以满足卫星建链的性能要求,所以设定纬度rs到re之间为可建链区。首先设定允许建链距离d,然后根据d将可建链区划分为多个对角线长度约为d的交叉建链区。允许建链距离最小为最近卫星距离dmin,最大为最远可视距离dmax。通过改变d,SCLBS可以动态调整每个卫星的可建链集大小m,最小为1,最大为可视卫星数M。对于最近卫星准则,m始终为1;对于最长可视时间准则,m始终为M。交叉建链区的示意图如图 5所示,其中m=5。
|
Download:
|
| 图 5 交叉建链区与星形结构 Fig. 5 Cross link-building areas and star structure | |
由2.1节的分析可知,同一时刻每个卫星与反向轨道上的多个卫星之间满足可建链条件,或者说相邻卫星的可建链集之间存在交集。为避免2个卫星选择相同的卫星建链,SCLBS按照星形结构确定建链卫星对(slast, i, sfirst, j)。如图 5所示,将卫星slast, 1进入第1交叉建链区的时隙记为t0,它的可建链集Nlast, 1(t0)包括sfirst, 1、sfirst, 2和sfirst, 3。
本文提出的SCLBS规定优先与最晚进入可建链集的卫星建立跨缝ISL,因此slast, 1将选择sfirst, 3建链。此时,slast, 2和sfirst, 2在上一个时隙已经建链,而slast, 3和sfirst, 1之间的距离将要超过d。在运行到下一个时隙之前的任一时刻t1,第1交叉建链区都有2条稳定的跨缝ISL,分别是(slast, 1, sfirst, 3)和(slast, 2, sfirst, 2),稳定建链数为m/2。在下一个时隙t0+Δt,slast, 0与sfirst, 4进入第1交叉建链区,网络拓扑与上一个时隙相同,同样按照星形结构进行建链。2个时隙第1交叉建链区的建链状态如表 1所示,其中-1表示即将断链,0表示准备建链,1表示稳定建链。
|
|
表 1 第一交叉建链区的建链状态 Table 1 The link-building status of the first cross link-building area |
在按照d对可建链区进行划分后,以卫星绕轨道运行一周为一个周期,记录一个周期内slast上的每个卫星进入交叉建链区起始纬度的时刻t,将它们作为一系列时隙,构成时隙集合Td。计算d取不同值的时候,t到t+Δt之间的稳定跨缝ISL总数L(d, t),并在一个周期内求和。增加的网络容量可以表示为整个周期内跨缝ISL总数与每条跨缝ISL可提供带宽B的乘积,通过最大化增加的网络容量可以得到最优的允许建链距离,即
| $d_{\mathrm{opt}}=\underset{d_{\min } \leqslant d \leqslant d_{\max }}{\operatorname{argmax}}\left(B \sum\limits_{t \in T_d} L(d, t)\right) .$ | (4) |
对上述问题求解得到最优允许建链距离dopt后,重新划分交叉建链区,记录每个交叉建链区的起始纬度,可以得到反向缝建链的参考纬度集合Rdopt。卫星在运行期间可以根据星历获取当前纬度,Sfirst或Slast的卫星运行到同一纬度时具有相同的建链条件。因此,通过记录参考纬度集合,将卫星运行到各交叉建链区起始纬度作为建立跨缝ISL的触发事件,SCLBS实现了反向缝的智能建链。每当卫星运行到集合Rdopt中的参考纬度时,就自动与上一个卫星断开跨缝ISL,与下一个卫星建立跨缝ISL。SCLBS的伪代码如表 2所示。
|
|
表 2 星形交叉循环建链策略 Table 2 Star cross looping link-building strategy |
本文设计的反向缝建链策略选择星形交叉结构是因为在前期采集分析数据的阶段发现反向缝两侧卫星的星历数据符合轮换对称性,这说明通过合理设计能够最大限度地实现反向缝处拓扑结构的循环性。通过研究和对比各个拓扑结构,星形结构在总体利用率和稳定性方面明显优于其他拓扑结构。星形结构保证每个卫星在进入交叉建链区时都选择与同一交叉建链区内距离最远的卫星建立跨缝ISL,所以不存在冲突问题,同时每条跨缝ISL的持续时间相对比较长,不会发生频繁的切换。此外,从图 5中可以看出,在地面业务点的角度,2个时隙t0和t0+Δt的网络拓扑完全相同。SCLBS的循环性为整个卫星通信系统提供了稳定的网络拓扑,让跨缝ISL的变化对地面业务点是不可见的。得益于此时网络拓扑的连续性,地面业务点的通信方案不需要进行任何改变。
在实际应用场景中,地面控制中心按照设计好的星座提前统计反向缝处卫星的星历数据,然后运行SCLBS,集中式计算得到全局最优的建链策略,将建链策略的具体指令上传到反向缝处的卫星。建链卫星根据指令在相应的纬度偏转激光终端,同时进一步根据实时位置分布式计算跟踪和捕获的参数,实时调整激光终端,完成跨缝ISL的建立。
3 实验与分析本节介绍仿真实验的参数设置,对SCLBS进行仿真,通过与其他建链策略对比,分析它在优化传输时延和路由跳数方面的表现。
3.1 实验设置使用Satellite Tool Kit (STK)软件对SCLBS进行仿真,它是Analytical Graphics公司提供的一款分析工具软件,科研工作者或工程师可以使用它的集成化仿真环境对陆地、海洋、航空与太空设备进行复合分析。
1) 系统参数
仿真基于Walker极轨道星座,其构型为Walker 200/10/5,轨道倾角为89°,轨道高度为1 025 km。星座共有10个轨道,平均间隔为18.6°;每个轨道上运行有20个卫星,同轨卫星间的夹角为18°。星间链路主要通过激光终端完成通信,激光终端具备指向、获取和跟踪等功能,精度符合反向缝建链对方位角和俯仰角的旋转要求[17]。极轨道星座和激光终端的详细参数分别如表 3和表 4所示。
|
|
表 3 极轨道星座参数 Table 3 Polar orbit constellation parameters |
|
|
表 4 激光终端参数 Table 4 Laser terminal parameters |
2) 业务模型
在1.2节业务模型的基础上,利用虚拟拓扑法将地球表面划分为200个业务区域,每个业务区域的经纬度大小为18°×18°。如图 6所示,分别表示飞机、船舶以及复合业务的业务量分布,每个业务区域里的数字表示当前区域的业务量指数。其中混合业务场景将飞机业务场景和船舶业务场景直接混合,可以更真实地反映出实际应用的业务量分布。受地球自转和轨道漂移等因素影响,以地面为参照物,反向缝会自东向西平移,周期约为24 h。因此本次仿真的周期设为24 h,步长设为60 s,仿真的开始时间为2020年10月12日4时。

|
Download:
|
| 图 6 不同业务场景的业务量分布 Fig. 6 Business volume distribution in different business scenarios | |
3) 对比算法
目前针对反向缝建立跨缝ISL的研究比较有限,为验证SCLBS的有效性,本文在选取对比算法时,参考同样具有频繁切换问题的星地之间馈电链路的切换准则。将SCLBS与基于最近卫星准则的建链策略(nearest satellite criterion link-building strategy, NSBS)、基于最长可视时间准则的建链策略(longest visible time criterion link-building strategy, LVTBS)和不跨缝建链策略(no cross seam link-building strategy, NCSBS)进行对比。
NSBS将星地间的最近卫星切换准则直接用于反向缝建链,认为跨缝ISL距离越小,传输速率越快,可以提供的通信服务质量越高。在选择建链卫星时,所有卫星节点都会时刻选择星间距离最短的卫星建立跨缝ISL。因为轨道内卫星等间距分布,轨道交点附近不属于可建链区,所以不会出现2个卫星选择同一卫星建立跨缝ISL的情况,解决了冲突问题。
LVTBS将星地间的最长可视时间准则直接用于反向缝处建链,认为跨缝ISL持续时间越长,连接越稳定,可以提供的通信服务质量越高。在选择建链卫星时,所有卫星节点都会选择与可视范围内最远的卫星建立跨缝ISL,直到建链的2个卫星之间不可见。这种建链策略保证每条跨缝ISL的持续时间最久,最大限度地降低链路切换带来的时间开销。
NCBS表示不在反向缝处建立跨缝ISL。因为反向缝处的卫星相对运行速度快,建链情况复杂,所以部分系统选择不在反向缝处建链,通过多次轨内和轨间转发实现跨缝传输。这种建链策略实现简单,但是会极大增加网络的传输时延,主要作为以上3种建链策略的对照。
3.2 结果与分析在上述实验参数和业务模型的基础上,使用SKT对SCLBS、NSBS、LVTBS以及NCSBS进行仿真。按照图 6的业务量分布,有跨缝通信需求的卫星主要集中在反向缝两侧的3个轨道内。首先根据不同业务场景的业务量分布随机生成一个周期内需要跨缝通信的卫星对,然后使用不同的建链策略在反向缝处建立跨缝ISL,最后计算网络的传输时延与路由跳数对建链策略进行分析。
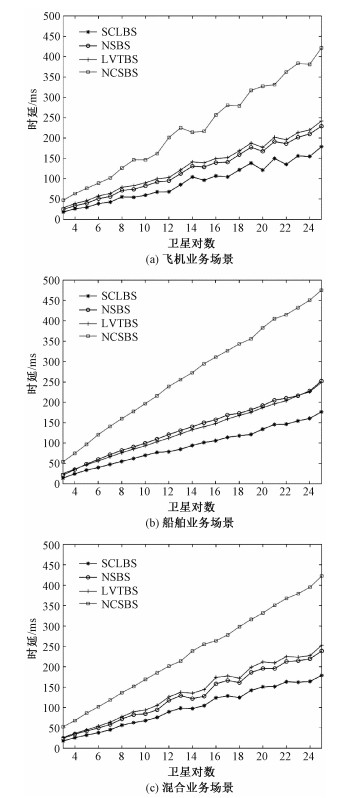
首先对比不同建链策略的传输时延表现,结果如图 7所示,横坐标为一个周期内需要跨缝通信的卫星对数量,纵坐标为卫星网络的总体传输时延。与飞机和复合业务相比,船舶业务场景下的传输时延与卫星对数成强相关。因为这种业务场景下的业务量分布更加集中,跨缝通信的卫星对相对固定。飞机业务场景的整体业务量分布更加分散,生成的跨缝通信卫星对随机性更大,传输时延容易出现波动。比如源卫星和目的卫星大量出现在远离反向缝的第3轨道上,即使业务量小,总体传输时延也可能比较大。混合业务场景将飞机业务场景和船舶业务场景直接混合,所以时延波动情况介于二者之间。因为在采集的原始数据中船舶业务量本身小于飞机业务量,所以混合业务场景的的仿真结果更加贴近飞机业务场景。从整体趋势看,各业务场景下传输时延和卫星对数都是正相关。
|
Download:
|
| 图 7 不同建链策略的网络传输时延 Fig. 7 Network transmission delay in different link-building strategies | |
然后对不同建链策略进行对比,同样如图 7所示。可以看到在所有业务场景下,SCLBS都是最优的。NCSBS因为没有在反向缝处建立跨缝ISL,遇到需要跨缝通信的业务需求时,只能通过大量的轨内和轨间转发,没有办法直接传输数据。它的传输时延最大,是其他建链策略的2~4倍。NSBS和LVTBS的时延表现比较接近,因为反向缝处卫星相向运动,最近卫星会经常发生变化,所以NSBS的每条跨缝ISL持续时间短。这种建链策略会导致卫星频繁切换跨缝ISL,造成非常大的时间开销。LVTBS的每条跨缝ISL持续时间长,不会频繁切换,但是过远的传输距离会导致链路衰减严重,同时在可建链区的边界处有可能发生建链冲突。SCLBS在两者之间进行权衡,通过选择最优的允许建链距离,提高网络容量的同时明显降低了系统的传输时延。因为严格按照星形结构建链,不会发生冲突。与NSBS相比,切换频率比较低。从图中可以看出,相比于NSBS和LVTBS,SCLBS的时延降低约30%,相对于NCSBS,降低约60%。
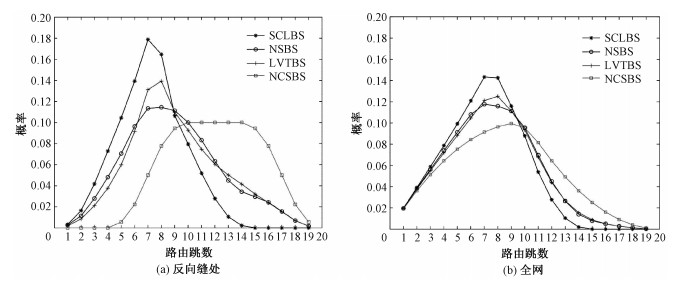
最后从网络拓扑方面分析几种建链策略的性能,仿真计算每种建链策略下反向缝处和全网的路由跳数分布,结果如图 8所示。与前面分析一致,通过优化反向缝处的建链策略,无论是反向缝处还是全网的路由跳数都有明显降低。在使用SCLBS对反向缝智能建链后,反向缝处的最大路由跳数由19跳降低到14跳,低路由跳数占比明显高于其他几种建链策略。对于全网路由跳数,SCLBS的低路由跳数占比也更低,全网平均路由跳数从8.5降低到6.8。
|
Download:
|
| 图 8 不同建链策略的路由跳数分布 Fig. 8 Route hop distribution in different link-building strategies | |
各个建链策略的低路由跳数占比如表 5所示。对于SCLBS,反向缝处路由跳数中低于10跳的占比大约为83%,而在NSBS、LVTBS和NCSBS中分别为59.6%、60%和35%。对于全网路由跳数,在SCLBS的优化下,低于10跳的路由跳数占比为90.6%,而在NSBS、LVTBS和NCSBS中这一占比分别为81.9%、82.1%和71.3%。
|
|
表 5 低路由跳数占比 Table 5 Percentage of low route hops |
综上所述,与NSBS、LVTBS和NCSBS相比,SCLBS在传输时延和路由跳数上的优化明显,对于不同业务场景,SCLBS都有优秀的表现。
4 结论本文针对极轨道LEO卫星网络的反向缝建链问题,提出一种星形交叉循环建链策略SCLBS。首先参考卫星的允许建链距离,将反向缝处的可建链区划分为多个交叉建链区。然后在交叉建链区内按照星形结构建链,通过在跨缝ISL的持续时间和数量之间进行权衡,优化网络容量,寻找最优的允许建链距离dopt。最后使用dopt重新对可建链区进行划分,记录每个交叉建链区的起始纬度集合,利用星历数据和起始维度集合实现反向缝智能建链。使用ADS-B和AIS实时采集的数据建立业务模型对SCLBS进行仿真,结果表明与其他建链策略相比,SCLBS可以降低30%~60%的传输时延,将全网平均路由跳数从8.5降低到6.8,明显提升LEO卫星网络的传输性能。
| [1] |
3GPP. TR 38.821 v16.0.0: Solution for NR to support non-terrestrial networks (NTN)[R/OL]. (2020-01-16)[2021-02-05]. https://www.3gpp.org/ftp/Specs/archive/38_series/38.821/38821-g00.zip.
|
| [2] |
刘沛龙, 陈宏宇, 魏松杰, 等. LEO卫星网络海量遥感数据下行的负载均衡多径路由算法[J]. 通信学报, 2017, 38(S1): 135-142. |
| [3] |
Tian F, Huang L L, Liang G, et al. An efficient resource allocation mechanism for beam-hopping based LEO satellite communication system[C]//2019 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB). Jeju, Korea (South): IEEE, 2019: 1-5.
|
| [4] |
刘婉莹, 夏师懿, 姜泉江, 等. 低轨卫星网络基于跳波束的资源调度算法[J]. 中国科学院大学学报, 2020, 37(06): 805-813. |
| [5] |
Ferreira A, Galtier J, Penna P. Topological design, routing, and handover in satellite networks[M]. New York, USA: John Wiley & Sons, 2002: 473-493.
|
| [6] |
De Sanctis M, Cianca E, Ruggieri M. Ip-based routing algorithms for Leo satellite networks in near-polar orbits[C]//2003 IEEE Aerospace Conference Proceedings (Cat. No. 03TH8652). Big Sky, MT, USA: IEEE, 2003: 1273-1280.
|
| [7] |
Ekici E, Akyildiz I F, Bender M D. A distributed routing algorithm for datagram traffic in LEO satellite networks[J]. IEEE/ACM Transactions on Networking, 2001, 9(2): 137-147. Doi:10.1109/90.917071 |
| [8] |
Gavish B, Kalvenes J. The impact of intersatellite communication links on LEOS performance[J]. Telecommunication Systems, 1997, 8(2/3/4): 159-190. |
| [9] |
Yeo B S, Turner L F. An approach to the modeling of counter-rotating seam communication links for LEO satellite systems[C]//2004 IEEE Wireless Communications and Networking Conference (IEEE Cat. No. 04TH8733). Atlanta, GA, USA: IEEE, 2004: 2016-2020.
|
| [10] |
Guo Z, Yan Z. A weighted semi-distributed routing algorithm for LEO satellite networks[J]. Journal of Network and Computer Applications, 2015, 58: 1-11. Doi:10.1016/j.jnca.2015.08.015 |
| [11] |
Jamalipour A, Chen J. Performance study of handoff schemes in broadband ATM mobile satellite networks[C]//ATM 2000. Proceedings of the IEEE Conference on High Performance Switching and Routing (Cat. No. 00TH8485). Heidelberg, Germany: IEEE, 2000: 501-508.
|
| [12] |
Gkizeli M, Tafazolli R, Evans B. Performance analysis of handover mechanisms for non-GEO satellite diversity based systems[C]//GLOBECOM'01. IEEE Global Telecommunications Conference (Cat. No. 01CH37270). San Antonio, TX, USA: IEEE, 2001: 2744-2748.
|
| [13] |
卢勇, 赵有健, 孙富春, 等. 卫星网络路由技术[J]. 软件学报, 2014, 25(05): 1085-1100. |
| [14] |
Tang F L, Zhang H T, Yang L T. Multipath cooperative routing with efficient acknowledgement for LEO satellite networks[J]. IEEE Transactions on Mobile Computing, 2018, 18(1): 179-192. |
| [15] |
Xia S Y, Jiang Q J, Zou C, et al. Beam coverage comparison of LEO satellite systems based on user diversification[J]. IEEE Access, 2019, 7: 181656-181667. |
| [16] |
Chen L, Zhang Q, Li M L, et al. Joint topology control and routing in IEEE 802.11-based multiradio multichannel mesh networks[J]. IEEE Transactions on Vehicular Technology, 2007, 56(5): 3123-3136. |
| [17] |
Qi S Y, Zhang Q, Xin X J, et al. Research on scanning method in satellite laser communication[C]//201918th International Conference on Optical Communications and Networks (ICOCN). Huangshan, China: IEEE, 2019: 1-3.
|
 2023, Vol. 40
2023, Vol. 40 


