2. 浙江大华技术股份有限公司,杭州 310053
2. Zhejiang Dahua Technology Co., Ltd, Hangzhou 310053, China
自然对流换热是一种生活和工程应用中常见的对流换热方式,其驱动原理与强迫对流不同,流体运动仅由浮力引起,而浮力通常是由温度变化引起的密度梯度和重力共同作用的结果[1]。尽管自然对流的换热系数小于强迫对流,但是简单的驱动原理和低成本等优点使其在许多工业领域或设备中得到广泛使用,如球形电子设备、循环流化床、固定床气化炉[2-3]和核工程设备中。后者包括加速器驱动次临界堆系统(accelerator driven subcritical system, ADS)的流态固体靶[4]和安全性高的第4代核反应堆——球床式高温气冷反应堆的堆芯[5]。
在针对球形颗粒的自然对流换热早期阶段,大部分学者的研究对象集中在单球上。由于NS方程的强非线性,单球自然对流早期研究成果大多借助实验得到。Yuge[6]研究1≤Gr≤105范围内定温单球在空气中的自然对流换热。Amato和Chi[7]将Gr数进一步扩展,分析3×105≤Gr≤8×108范围内的定温单球在水中的换热,其宽广的Gr数范围涵盖层流、过渡和湍流状态的开端。除上文提到的针对常见的空气和水的研究外,学者们也通过实验研究其他许多介质的自然对流换热。Kranse和Schenk[8]研究108 < Gr < 109和Pr=8.3范围内液态苯中熔化苯球的自然对流换热情况,Tsubouchi等[9]研究10-10 < Gr < 5×108和0.71 < Pr < 105范围内的介质为油的单球换热。上述研究者也得到了Nu与Gr、Pr数或Ra数之间的关联式。Churchill[10]总结前人实验结果并将针对单球的自然对流换热关联式适用范围扩展到Ra≤1011和Pr≥0.7。由于其宽广的适用范围和高精度,该关联式得到了工业界广泛使用和作为数值模拟的常见验证对象, 并被传热学经典教材收录[1]。
随着计算机性能的提高和各种稳定的、精确的数值算法的提出,越来越多的学者开始通过数值模拟方法研究球类自然对流换热问题。Jia和Gogos[11-12]数值模拟10 < Gr < 108,Pr=0.72和7范围内的定温单球在稳态和瞬态情况下的层流自然对流换热情况。Yang等[13]分析Pr数(0.02、0.7、7和100)对于定温单球层流自然对流换热的影响。此外,许多学者研究幂流体的自然对流换热,详细介绍可参见文献[14]。
除对于单球的自然对流研究,一部分学者重点关注竖直布置两球、三球结构。Chamberlain等[15]实验得到10≤Ra≤107范围内竖直两球的自然对流换热关联式,其与通过Raithby-Hollands方法[16]获得的结果平均误差约为3%。另外,通过文中提到的修改方案,作者将关联式扩展到了其他Pr数流体和更低的Ra数。Jafarpur和Yovanovich[17]提出0 < Ra < 108和全范围Pr数内的竖直两球自然对流换热的半经验关联式,其研究方案基于理论扩散极限法(Ra→0)的线性叠加和薄边界层限制。Musong等[18]采用三维浸入边界法(immersed boundary method, IBM)数值研究5 < Gr < 500和5 < Pr < 125范围的两球和三球的自然对流换热。此外,Zhang等[19]探索间距对于两球自然对流换热的影响,得到2≤S/D≤24, Ra=105和Pr=0.72范围两球Nu和S/D的关联式。
鉴于自然对流换热研究具有极其重要的学术价值,虽然简单单球和双球结构的关联式已存在于教科书和手册之中,但是对于多球结构的相关研究还很少。另外,在实际工程应用中多球结构的布置种类十分丰富。跟其他核工程一样,ADS流体固体靶也要考虑如当系统故障、电源失效等极端情况下反应堆的安全运行及如何防止堆芯过热问题。因此研究通过自然对流这种非能动的方式带走靶内钨球的体积热对系统安全运行很重要。虽然Liu等[14]研究紧密接触水平三球这一简单且基本结构的自然对流换热,但对于高温气冷反应堆的堆芯和ADS流态固体靶中的球床等领域,其中存在的大数量的多球的自然对流换热无法通过简单单球、双球、三球结构进行预测。因此,本文通过将“极限”的数学思想引入三维数值模拟中,研究顺排布置下的水平单层球自然对流换热,模拟得到Nu=f(N)关联式,同时获得不受周围球数增加影响的中心球Nu数。其他结果包括不同排列数下的温度、流线分布,局部阻力系数分布和局部努塞尔数。上述研究将丰富多球自然对流传热领域的结果,既能为ADS流态固体靶结构的传热优化设计提供参考,也能为其他包含大数量多球系统的工业应用提供可靠依据。此外,本文用到的三维计算模型是基于二维Bejan模型[19]扩展得到的,该模型计算量小、且计算结果准确,这将在下节给予详细说明。
1 模型及方法本文研究Gr=103情况下排列数范围为3×3至15×15的水平单层球自然对流换热情况,将“极限”的数学思想引入数值模拟的具体操作中,通过逐步模拟3×3排列、5×5排列直至具有代表性的(2N+1)×(2N+1)排列(数字代表每排每列的球数, N≥1且为整数)来逼近目标情况,示意图见图 1。每个球表面温度维持Tw不变,且高于环境温度T∞。由于温差存在,附近空气被加热,在热膨胀系数作用下,其密度减小。附近流体进而会在浮升力的驱动下向上运动并且和球形结构进行换热。随着中心球周围的球不断增多,当Nu数逐渐趋近某个值时,即表示中心球换热过程不再受周围球数增加的影响,此时该值就约等于大数量的球床中任意单个球的Nu数。

|
Download:
|
| 图 1 “极限”的数学思想 Fig. 1 Idea of the limit in mathematics | |
在层流自然对流传热的数值研究中,浸没在广延和静止空气的物体需要足够大的计算空间,即保证边界层能自由地发展而不受外边界影响。在前人研究中,习惯上将球体浸入足够大的外环境中,此时外内边界的比率d∞/D约为12.5、25和40[14]。然而,巨大的计算域会严重降低计算效率。为此,Bejan等[20]在5~8根水平错排管束的自然对流优化换热计算中提出一种更经济的二维计算模型。与常规模型相比,二维Bejan模型在远端气体出口附近设置一个入口来中和换热过程中由于密度变化产生的压力差,避免烟囱效应,同时可以使计算域的宽度减小到d∞/D=3或10从而大幅度提高计算效率。需要指出的是:烟囱效应是指在细长区域内流体被施加一个额外的加速度现象,其会影响计算的准确性。该模型在对称条件下的应用已被证明是可行的,包括在二维条件下的半球(轴对称结构)[19, 21]和圆柱(对称结构)[22-24]。然而它不适用于本文研究的顺排布置的水平单层球结构。因此本文基于二维Bejan模型,提出拓展后的三维模型,减少计算域和提高计算效率的同时避免烟囱效应的产生,如图 2所示。此外,局部结果的展示采用图 2(b)中的球坐标系(r, θ, φ)以便于分析后文数据。

|
Download:
|
| 图 2 三维拓展计算模型 Fig. 2 Expanded 3D computational model | |
这里以3×3排列水平单层球为例解释三维模型,如图 2(a)所示。坐标原点在中心球的球心。由于流动对称性,仅选取切割后的1/8等腰直角三棱柱(由灰色面组成)的拓展模型进行模拟,这样可以极大地减少计算量。对于切割后的拓展模型,每个球体和空气的温度分别保持恒定值Tw和T∞(Tw>T∞)。这里假设空气(Pr= 0.72)不可压缩,其热物性参数通过恒定的膜温Tm(=(Tw+T∞)/2)来获得,除了Z方向上的动量方程的密度项中,使用布辛涅斯克假设(Boussinesq approximation)说明密度变化和温度变化之间的关系:
| $ \left(\rho_{\infty}-\rho\right)=\rho \beta\left(T-T_{\infty}\right) . $ | (1) |
为减少误差,本文在数值模拟中使用大约1 K的温度差来保证布辛涅斯克假设的有效性。由于温差极小,空气可近似为理想气体,所以其热膨胀系数β可简化为β=1/Tm。另外,由于本文中自然对流是低速层流且采用空气不可压缩假设,所以能量方程中忽略黏性耗散和辐射。因此,三维、稳态、常物性等条件下的无量纲控制方程可以简化成如下:
连续性方程
| $ \frac{\partial u^*}{\partial X^*}+\frac{\partial v^*}{\partial Y^*}+\frac{\partial w^*}{\partial Z^*}=0. $ | (2) |
X方向动量方程
| $ \begin{gathered} u^* \frac{\partial u^*}{\partial X^*}+v^* \frac{\partial u^*}{\partial Y^*}+w^* \frac{\partial u^*}{\partial Z^*}= \\ -\frac{\partial p^*}{\partial X^*}+\frac{1}{\sqrt{G r}} \Delta u^*, \end{gathered} $ | (3) |
Y方向动量方程
| $ \begin{gathered} u^* \frac{\partial v^*}{\partial X^*}+v^* \frac{\partial v^*}{\partial Y^*}+w^* \frac{\partial v^*}{\partial Z^*}= \\ -\frac{\partial p^*}{\partial Y^*}+\frac{1}{\sqrt{G r}} \Delta v^*, \end{gathered} $ | (4) |
Z方向动量方程
| $\begin{gathered} u^* \frac{\partial w^*}{\partial X^*}+v^* \frac{\partial w^*}{\partial Y^*}+w^* \frac{\partial w^*}{\partial Z^*}=\\ -\frac{\partial p^*}{\partial Z^*}+\frac{1}{\sqrt{G r}} \Delta w^*+T^*. \end{gathered} $ | (5) |
能量方程
| $ u^* \frac{\partial T^*}{\partial X^*}+v^* \frac{\partial T^*}{\partial Y^*}+w^* \frac{\partial T^*}{\partial Z^*}=\frac{1}{\operatorname{Pr} \sqrt{G r}} \Delta T^* . $ | (6) |
其中拉普拉斯算子Δ定义为
上述控制方程中无量纲变量的定义,图 2(a)中计算域的边界条件的设定和文献[14]保持一致。
控制方程(2)~方程(6)通过有限体积法进行离散化。压力-速度耦合采用SIMPLE算法,在离散选项组中,梯度项和压力项分别采用最小二乘法和二阶格式。动量和能量方程中的对流项采用精度高的二阶迎风格式。控制方程收敛标准设置为10-6量级。此外还通过监视Nu和C参数来判断数值迭代求解是否收敛。
在开始本文研究内容之前,需要进行区域无关性验证和网格无关性验证,消除计算域大小和网格数量对于结果的影响。入口段和出口段的垂直长度参考文献[14]使用恒定的3D,如图 2(a)所示。对于计算域宽度d∞,(2N+1)×(2N+1)排列模型选择d∞=0.52N+1D+N×0.01D+2D。举例来说,3×3排列模型选择d∞=1.5D+0.01D+2D,1.5D+0.01D表示中心球球心到最外围球的距离,其中0.01D表示3×3排列模型只存在一个间隙,2D表示最外围球到模型外边界的距离。间隙的存在是由于模型无法做到任意两球紧密接触,因此在网格划分时采用极小间距(0.01D) 来代替紧密接触,同时避免产生质量差的网格。这里要说明的是,本文模拟的多组排列模型中最外围球到模型外边界的距离均使用2D,这是由于固定的Gr数使得温度和速度边界层不会因为排列数的增多而有剧烈变化。
为验证上述计算域尺寸的合理性,以3×3排列模型为例进行区域无关性验证,结果如表 1所示。当计算域长度和宽度都增大1倍时,如区域D1和D3,所有球的
|
|
表 1 区域无关性验证(3×3排列) Table 1 Domain independence tests for 3×3 array |

|
Download:
|
| 图 3 3×3排列模型网格示意图 Fig. 3 Schematic representation of the computational grid for 3×3 array | |
另一方面,对于自然对流的数值研究,网格是影响计算结果的另一个重要因素,对其进行合理划分不仅可以得到更加准确的结果,还可以有效减少网格数量,减少不必要的计算。本文采用非结构化网格,网格的最小正交质量保持在0.4左右。图 3是3×3排列模型计算域的网格划分示意图,采用三视图的形式进行展示。其中正视图与XZ平面不平行,而是在俯视图上的φ=π/4切面;侧视图与YZ平面平行;俯视图在XY平面上的水平剖面。从图中可以发现区域被划分为两部分:对应于多球附近区域的区域Ⅰ,其大小是从中心球球心沿Y方向延伸2.51D,沿Z方向延伸1.5D;区域Ⅱ则对应着余下的外部区域。在区域Ⅰ,速度和温度边界层中的速度和温度梯度变化剧烈,特别是中心球周围区域,为捕获球表面附近较大的速度和温度的梯度以及多球之间的相互作用,在该区域使用非常精细的网格。然而,对于区域Ⅱ,其速度和温度则变化缓慢,因此在该区域使用相对较粗的网格以避免计算工作的浪费。结果如表 2所示,对于3×3排列,当网格数量增大1倍时,如网格G1和网格G2,
|
|
表 2 网格无关性验证(3×3排列) Table 2 Grid independence tests for 3×3 array |
综合上述区域无关性验证和网格无关性验证,顺排布置的水平单层球自然对流换热模型使用以下参数:纵向长度Z=±3D, 横向宽度d∞=0.52N+1D+N×0.01D+2D,另外网格始终使用G1。
2 结果及讨论 2.1 模型方法验证除进行区域和网格无关性验证外,还需对计算模型本身进行验证。虽然前人已经验证了二维情况下Bejan等提出的模型的正确性和精确度[19, 21-23],但为保证三维拓展模型(切割后)的正确性和精确性,本文以三维单球为验证对象,与前人的实验和数值结果[10-11, 25]进行比较,结果如表 3所示。通过三维拓展模型得到的Nu数与Jia和Gogos[11]以及Prhashanna和Chhabra[25]的数据符合较好,在不同Gr数下的误差均小于2%。其中,与Churchill[10]的数据进行比较,其误差随着Gr数的增加从8% 左右逐渐变为1% 左右,这是因为Churchill[10]的Nu数关联式拟合考虑多种介质的自然对流换热(包括空气、水和油等)。对于C,最大误差为4.2%,而与Prhashanna和Chhabra[25]在Gr=10时的数据相比,误差仅为0.77%。需要说明的是,表 3中的“/”表示Prhashanna和Chhabra的单球自然对流换热没有包含Gr=102和104情况下的结果。
|
|
表 3 三维单球的验证结果 Table 3 Verification results of three-dimensional single sphere |
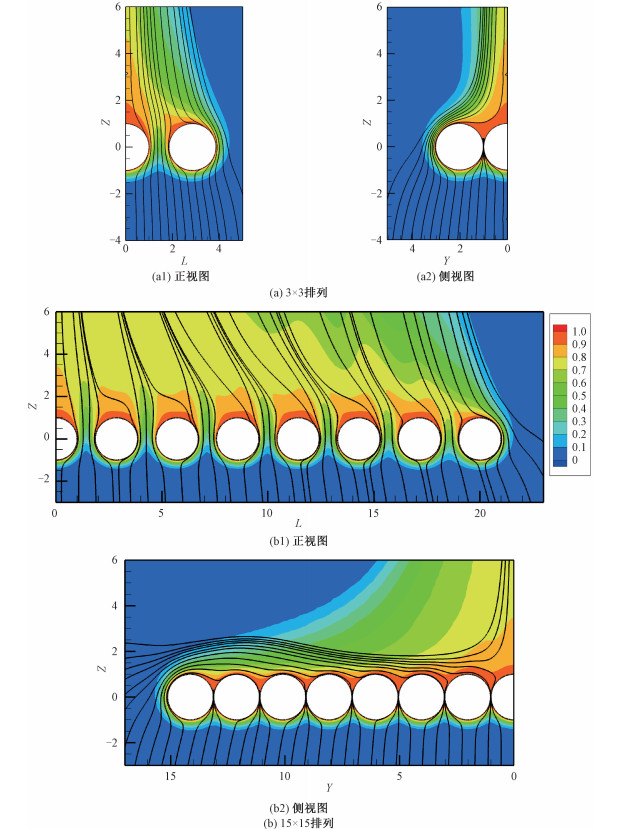
为了定性说明排列数对于水平单层球自然对流换热的影响,本节展示3×3和15×15排列的水平单层球自然对流的温度分布和流线分布。由于球面是定温的,所以持续与球周围的冷空气发生热交换,而这些冷空气吸热后产生密度差,进而在浮升力作用下围绕球体不断向上运动,在这个过程中还裹挟多球区域外围的大量空气来形成稳定运动的卷流。随着排列数的增加,最外围球附近的温度分布的整体情况没有改变,但是对于其他位置的大多数球,15×15排列的温度分布与3×3排列不相同,特别是对于层球间隙附近的温度场。从图 4(a1)和图 4(b1)的温度分布可以看出,随着排列数增加,层球间隙附近区域吸入了更多的冷空气。这是因为随着排列数增加,层球上方的热空气被进一步加热,在强浮力的驱动下向上运动,由此导致该区域负压增大,具体可见2.3节中的CP分布。虽然这会导致外围空气快速补充进来,但中间区域因为无法直接和这些补充的空气接触,从而会通过单层球的间隙从下方吸入大量冷空气,这使得球和周围空气换热增强,具体可见2.4节的Nu数分布。该负压区存在范围较广,基本涵盖大多数的球,且越靠近单层球排列的中心,负压越大,通过间隙吸入的冷空气越多。此外,与单球的温度和流线分布不同,由于外围空气向中间位置靠拢,单层球上方的温度边界层会受到挤压,流线产生明显的弯曲,这从图 4(a2)和图 4(b2)之间的温度和流线分布的对比可以看出。
|
Download:
|
| 图 4 不同排列数下水平单层球的温度分布和流线分布 Fig. 4 Isothermal and streamline contours in the vicinity of the horizontal multi-spheres | |
图 5中展示方位角为φ=π/4位置处中心球的自然对流换热的CF分布(图 5(a))和CP分布(图 5(b))。总的来说,随着排列数增加,CF逐渐增大,CP的绝对值也逐渐增大。这是因为层球上方的卷流随着排列数的增加受到的加热效应更强,导致层球附近区域负压增大,即压力梯度增大,由此增强了流体的流动能力。而且层球下游负压受排列数的影响更明显。对于某一排列数而言,随着θ的减小(从上游导向下游),中心球壁面附近的流体首先在顺压力梯度下加速,速度梯度也相应增大。当θ减小到π/2时,虽然流体在顺压力梯度下依然会加速,但因为受到下游卷流的影响,速度边界层逐渐增厚,速度梯度开始随着θ的减小而减小。当θ减小到3π/7时,流体在逆压力梯度下开始减速,在下游卷流的共同作用下,速度梯度减小幅度加大,并在θ=0~π/4区间达到最小且基本保持为零。

|
Download:
|
| 图 5 φ=π/4下中心球的局部阻力系数分布 Fig. 5 Variation of local drag coefficient along the surface of central sphere from 3×3 to 15×15 for φ=π/4 | |
图 6展示方位角为φ=π/4位置处不同排列数(从3×3至15×15)的Nu数的影响。总的来看,Nu数随着排列数增加而增大。这是由于对流效应随着排列数增加而增强,从而加大了球体和流体之间的换热,这种区别在上游区域更加明显。这是因为上游区域的温度边界层相对于下游区域受排列数的影响更大。对比13×13和15×15这2种排列,可以发现当排列数增加到一定限度后,Nu数分布基本不变,这表明本文引入的“极限”的数学思想的合理性。通常来说,Nu数随着θ的减小而单调递减,即球体底端的Nu数最大而顶端的Nu数最小。在θ=5π/8~π区域,Nu数变化不大。这是因为虽然流速的增加会增强换热,但中心球附近球体对流体的预热减小了温差。两种因素共同作用使得中心球Nu数变化不大。当θ从5π/8开始减小,附近球体对流体的预热作用增强,中心球Nu数逐渐减小。随着θ进一步减小,流体速度的减小使得Nu数减小幅度变大。在θ=0~π/4区间,换热方式主要是热传导,因为上方卷流及周围球体的作用,中心球和流体之间的温差较小,换热能力较弱。

|
Download:
|
| 图 6 φ=π/4下中心球的局部努赛尔数分布 Fig. 6 Variation of local Nusselt number along the surface of two horizontal spheres from 3×3 to 15×15 for φ=π/4 | |
Nu数由于关系到自然对流传热的平均速率而在实际的工程应用中扮演着重要角色,所以通过引入“极限”的数学思想来获得不受周围球数增加影响的中心球Nu数。这种极限情况下的Nu数能为有限空间内的有限球数的自然对流换热提供参考。另外在实际的数值模拟过程中,除接近极限情况下的排列数外,还模拟中间过程的不同排列数情况。一方面,拟合的Nu=f(N)关联式可以使得对于有限球数的自然对流换热的参考更加准确;另一方面也是考虑到三维模型网格数量大和计算缓慢的原因,通过循序渐进的数值模拟来探索前进。
图 7展示排列数N对于中心球Nu数的影响及其拟合关系。中心球的Nu数呈现出与N正相关分布。这是由于随着排列数增加,对流效应的增强使得中心球的Nu数升高。与Gr数相同情况下的单球的Nu数相比,单层球的中心球的Nu数处在更低的水平。Nu数所对应的换热速率的整体弱化是因为球与球的换热互相影响导致的。此外,为了更好预测极限情况下Gr=103情况下顺排布置的水平单层球的中心球Nu数,数值模拟结果已经通过拟合得到公式
| $ \overline{N u}=4.1628 \cdot\left(1-0.4301 \cdot 0.9329^{(2 N+1)}\right) . $ | (7) |

|
Download:
|
| 图 7 中心球的平均努赛尔数分布 Fig. 7 Average Nusselt number distribution of the central sphere | |
其中(2N+1)表示排列数,如图 1(c)所示。决定系数R2分别为0.999 4,且关联式与数值结果平均误差仅为0.15%,最大误差为0.25%,这些数据表明上述公式拟合程度极好。关联式减号后的部分为指数函数,即随着N的增加而趋向于零,所以可以预测中心球不受周围球数增加影响时的Nu数为4.162 8,这比Gr数相同情况下的单球的Nu数下降30.2%。
3 结论本文研究Gr=103情况下排列数范围为3×3至15×15的水平单层球自然对流换热情况,计划获得不受周围球数增加影响的中心球Nu数。其他结果包括温度和流线分布、局部阻力系数分布、Nu数分布和Nu数等。结论如下:
1) 随着排列数增加,卷流作用的增强使得单层球上方区域负压增大。这不仅导致层球上方温度边界层受到挤压,而且使得通过球体间隙从下方吸入的流体速度升高。越靠近单层球排列的中心,负压越大,吸入的流体速度越大。
2) 总的来看,Nu数与排列数呈正相关。由于上游区域温度边界层受排列数影响更大,排列数对该区域Nu数的影响更明显。通常来说,Nu数随着θ的减小而单调递减。对于θ=5π/8~π区域,Nu数随θ减小幅度较小。随着流体的减速及周围球体对中心球预热的增强,Nu数随θ减小幅度加大。在θ=0~π/4区间,Nu数达到最小。
3) 中心球的Nu数呈现出与排列数的正相关分布,且与单球相比,单层球中的中心球的Nu数处在更低的水平,这种整体弱化是因为球与球的换热互相影响导致的。中心球的Nu数与排列数拟合关系式为Nu=4.162 8 ·(1-0.430 1 ·0.932 9(2N+1))。从中可预测中心球不受周围球数增加影响时的Nu数为4.162 8,这比Gr数相同情况下的单球的Nu数下降30.2%。
| [1] |
Bergman T L, Lavine A S. Fundamentals of heat and mass transfer[M]. 8th ed. Hoboken: John Wiley & Sons, 2017: 540-576.
|
| [2] |
Openyshev P V, Sheremet M A. Influence of a porous insert on the fluid flow inside the gasifier shaft[J]. Key Engineering Materials, 2016, 685: 235-239. Doi:10.4028/www.scientific.net/kem.685.235 |
| [3] |
Pichler M, Haddadi B, Jordan C, et al. Effect of particle contact point treatment on the CFD simulation of the heat transfer in packed beds[J]. Chemical Engineering Research and Design, 2021, 165: 242-253. Doi:10.1016/j.cherd.2020.11.005 |
| [4] |
Yang L, Zhan W L. New concept for ADS spallation target: gravity-driven dense granular flow target[J]. Science China Technological Sciences, 2015, 58(10): 1705-1711. Doi:10.1007/s11431-015-5894-0 |
| [5] |
Yamoah S, Akaho E H K, Ayensu N G A, et al. Analysis of fluid flow and heat transfer model for the pebble bed high temperature gas cooled reactor[J]. Research Journal of Applied Sciences, Engineering and Technology, 2012, 4(12): 1659-1666. |
| [6] |
Yuge T. Experiments on heat transfer from spheres including combined natural and forced convection[J]. Journal of Heat Transfer, 1960, 82(3): 214-220. Doi:10.1115/1.3679912 |
| [7] |
Amato W S, Chi T. Free convection heat transfer from isothermal spheres in water[J]. International Journal of Heat and Mass Transfer, 1972, 15(2): 327-339. Doi:10.1016/0017-9310(72)90078-6 |
| [8] |
Kranse A A, Schenk J. Thermal free convection from a solid sphere[J]. Applied Scientific Research, Section A, 1966, 15(1): 397-403. Doi:10.1007/BF00411573 |
| [9] |
Tsubouchi T, Sato S, Masuda H. Effect of Prandtl number on the natural convection heat transfer of small particles[J]. Transactions of the Japan Society of Mechanical Engineers, 1964, 30(219): 1386-1393. Doi:10.1299/kikai1938.30.1386 |
| [10] |
Churchill S W. Comprehensive, theoretically based, correlating equations for free convection from isothermal spheres[J]. Chemical Engineering Communications, 1983, 24(4-6): 339-352. Doi:10.1080/00986448308940090 |
| [11] |
Jia H, Gogos G. Laminar natural convection heat transfer from isothermal spheres[J]. International Journal of Heat and Mass Transfer, 1996, 39(8): 1603-1615. Doi:10.1016/0017-9310(95)00259-6 |
| [12] |
Jia H, Gogos G. Transient laminar natural convection heat transfer from isothermal spheres[J]. Numerical Heat Transfer, Part A: Applications, 1996, 29(1): 83-101. Doi:10.1080/10407789608913780 |
| [13] |
Yang S, Raghavan V, Gogos G. Numerical study of transient laminar natural convection over an isothermal sphere[J]. International Journal of Heat and Fluid Flow, 2007, 28(4): 821-837. Doi:10.1016/j.ijheatfluidflow.2006.08.004 |
| [14] |
Liu Z Y, Chu Y, Liu J, et al. Numerical investigation of the laminar natural convection heat transfer from the equilateral triangular cluster of three horizontal spheres[J]. International Journal of Heat and Mass Transfer, 2019, 136: 924-937. Doi:10.1016/j.ijheatmasstranster.2019.02.084 |
| [15] |
Chamberlain M J, Hollands K G T, Raithby G D. Experiments and theory on natural convection heat transfer from bodies of complex shape[J]. Journal of Heat Transfer, 1985, 107(3): 624-629. Doi:10.1115/1.3247469 |
| [16] |
Raithby G D, Hollands K G T. A general method of obtaining approximate solutions to laminar and turbulent free convection problems[J]. Advances in Heat Transfer, 1975, 11: 265-315. Doi:10.1016/s0065-2717(08)70076-5 |
| [17] |
Jafarpur K, Yovanovich M M. Laminar free convective heat transfer from isothermal spheres: a new analytical method[J]. International Journal of Heat and Mass Transfer, 1992, 35(9): 2195-2201. Doi:10.1016/0017-9310(92)90063-x |
| [18] |
Musong S G, Feng Z G, Michaelides E E, et al. Application of a three-dimensional immersed boundary method for free convection from single spheres and aggregates[J]. Journal of Fluids Engineering, 2016, 138(4): 041304. Doi:10.1115/1.4031688 |
| [19] |
Zhang J, Liu J, Lu W Q. Study on laminar natural convection heat transfer from a hemisphere with uniform heat flux surface[J]. Journal of Thermal Science, 2019, 28(2): 232-245. Doi:10.1007/s11630-018-1051-y |
| [20] |
Bejan A, Fowler A J, Stanescu G. The optimal spacing between horizontal cylinders in a fixed volume cooled by natural convection[J]. International Journal of Heat and Mass Transfer, 1995, 38(11): 2047-2055. Doi:10.1016/0017-9310(94)00312-J |
| [21] |
Liu J, Zhao C J, Liu H, et al. Numerical study of laminar natural convection heat transfer from a hemisphere with adiabatic plane and isothermal hemispherical surface[J]. International Journal of Thermal Sciences, 2018, 131: 132-143. Doi:10.1016/j.ijthermalsci.2018.05.013 |
| [22] |
Liu J, Liu H, Zhen Q, et al. Laminar natural convection heat transfer from a pair of attached horizontal cylinders set in a vertical array[J]. Applied Thermal Engineering, 2017, 115: 1004-1019. Doi:10.1016/j.applthermaleng.2017.01.029 |
| [23] |
Liu J, Liu H, Zhen Q, et al. Numerical investigation of the laminar natural convection heat transfer from two horizontally attached horizontal cylinders[J]. International Journal of Heat and Mass Transfer, 2017, 104: 517-532. Doi:10.1016/j.ijheatmasstransfer.2016.08.075 |
| [24] |
石宏岩, 刘捷, 卢文强. 水平紧密接触品字形三圆管自然对流换热的数值模拟[J]. 中国科学院大学学报, 2018, 35(5): 595-601. Doi:10.7523/j.issn.2095-6134.2018.05.004 |
| [25] |
Prhashanna A, Chhabra R. Free convection in power-law fluids from a heated sphere[J]. Chemical Engineering Science, 2010, 65(23): 6190-6205. Doi:10.1016/j.ces.2010.09.003 |
 2023, Vol. 40
2023, Vol. 40 


