2. 中国科学院大学工程科学学院, 北京 100049
2. School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China
瑞利-贝纳德对流(Rayleigh-Bénard,RB对流)是一种由温差产生的浮升力引起流体运动的经典流体力学现象,它广泛存在于自然界和工业应用领域[1-3],如地幔对流运动与大气对流、换热器中的热对流、微电子设备冷却等。对这种现象的研究最先开始于20世纪初,Bénard[4]和Rayleigh[5]通过实验研究建立了相应的对流运动控制方程。此后大量国内外学者通过数值模拟和实验探索流体的对流特性和物理机理。Chandrasekhar[6]从稳定性的角度出发研究了RB对流产生不稳定流动现象的条件。Oberbeck[7]将湍流热对流系统进一步简化:只考虑流体的密度与温度线性相关,流体其余的物性参数,如热扩散系数、热膨胀系数、黏性系数均不随温度发生改变。Grossmann和Lohse[8-10]提出的GL理论分析了能量耗散率和温度耗散率对系统的影响。认为对流系统的传热与流动结构息息相关,羽流由蘑菇形头冠和茎干组成,在混合区,蘑菇状羽流和片状羽流相互转化,并通过分析给出了流动和传热的标定律。周全和夏克青[11-12]发现RB系统中热量的传递主要是通过边壁附近的羽流来完成的,当羽流数目增加时,系统的换热效率也得到增强。大尺度环流是一种在RB系统中充分发展时存在的流动结构,Sun和Xia[13]通过实验测量了大尺度环流频率和对流壁面处速度的概率密度函数,得到大尺度环流的特征速度,总结了Re ~ Ra1/2的标定律关系。大尺度环流下准二维涡胞运动,时常伴随着角向运动、停滞和反转等现象。然而,上述研究主要集中于普朗特数(Pr, 表征黏性扩散和热扩散的比值)较大的常规流体,针对于液态金属这种普朗特数极低(~0.03)的流体研究较少。然而,液态金属热对流同样广泛存在于工业应用领域,例如核聚变装置中包层的热量输运,以及电磁冶金的晶体生长过程的对流控制等。这种流体将在更低的Ra数下过渡到湍流状态,更容易出现大尺度湍流流动[14]。目前对于液态金属的对流现象研究较少,其形成湍流的方式和大尺度的流动结构的机理尚不清楚,亟需开展大量的研究工作。然而,通过实验的方法能直接获得液态金属内部的速度和温度信息,不仅能更好地理解液态金属的对流特征,还能验证数值模拟和理论分析的相关结果,具有重要的意义。
对于液态金属而言,当Ra数略高于临界值时,对流涡胞会发生振荡,进一步增大瑞利数,流动容易形成湍流,腔内流体速度呈现各向异性波动。当磁场作用于液态金属对流时,洛伦兹力破坏了无磁场环境下惯性力与黏性力的平衡。根据磁场的方向和强度,涡胞会产生不同的运动形态。当施加水平或垂直磁场后,发生振荡的临界值增大,不易形成湍流,呈现规则的涡胞运动[15-16]。同时,一系列的理论研究也表明[17-18],对于液态金属等低Pr数流体,无磁场下准二维状态容易向三维状态转变,而磁程场的存在推迟了对流的振荡以及下一步转捩的发生[19-20]。
对液态金属在水平无限大平面中RB对流的理论研究表明[6],垂直磁场延缓了对流运动的发生,临界瑞利数随着磁场强度的平方成比例增大,水平波数也随之增大;而当施加水平磁场,临界瑞利数与水平波数则不发生改变[21],仅改变对流的对称轴方向,使之沿磁场的方向排列。Yu等[22]通过数值模拟探索了垂直磁场作用下的流场结构和流态的演变,而水平磁场作用下的流态变化机理仍值得进一步的研究。Horanyi等[23]通过开展液态钠在大宽高比的圆柱体中的对流现象的研究,获得了Ra数大于106时,Nu数与Ra数的标定律关系。Burr和Müller[24]研究磁场作用下钠钾合金在矩形方腔中的对流特性。Aurnou和Olson[25]利用液态金属镓研究磁场和旋转作用时,矩形方腔内液态金属的对流特性。Takeshita等[26]通过宽高比较小的圆柱腔体研究水银在大Ra数下的湍流特性。这些实验通过研究不同Ra数下腔内的温度波动特性,间接分析了RB系统的大尺度流动特征,但缺乏对液态金属内部速度的直接测量。然而,液态金属不透明,无法采用激光的方法(如粒子图像测速、激光多普勒测速等)来获得其内部的速度分布。超声波因具有对不透明介质的较好穿透性以及在传播过程中遇到运动障碍物产生的多普勒效应,而被认为是测量不透明液态金属内部速度分布的一种可行方法。周仲恺等[27]通过超声波多普勒测速技术研究强磁场下液态金属在竖直平板内的流动过程。Yanagisawa等[28-29]系统性地采用超声波测量方法,展现了液态金属在方腔内流动结构的转变、反转等过程。Vogt等[30-31]采用实验和数值模拟结合的方法,定量地表征了无磁场和磁场影响下液态金属在方腔和圆柱内的热对流结构,补充了磁场作用下液态金属流动结构变化的相图,通过调节Ra数和Chandrasekhar数的比值可以获得多种涡胞的运动形态。Akashi等[32]通过多个超声波探头在2个不同方向布置的方式,基于有限的速度场信息,较好地展现了无磁场下液态金属在方腔内的大尺度环流特征。Zürner等[33]对宽高比为1的圆柱内液态金属热对流的流动和传热特性开展了详细的研究,通过对多个超声波探头和温度探头测量的速度和温度信息分析圆柱内的液态金属大尺度动量和热量传递过程。在数值模拟方面,Lim等[34]模拟方腔内的准静态磁对流的传热增强现象,并通过对热边界层厚度和速度边界层厚度的分析,解释了磁场存在下液态金属对流传热特性变化的规律。然而,目前对磁场作用下的液态金属热对流特性研究还处于起步阶段,缺乏从速度测量的角度来详细表征磁场存在时的各种流动结构特征、速度和温度边界层的尺度以及液态金属磁热对流的流动和传热标定律等。
本文以此为背景,基于多通道的超声波多普勒测速方法,对宽高比为0.5的方腔内液态金属热对流结构进行详细测量和分析。
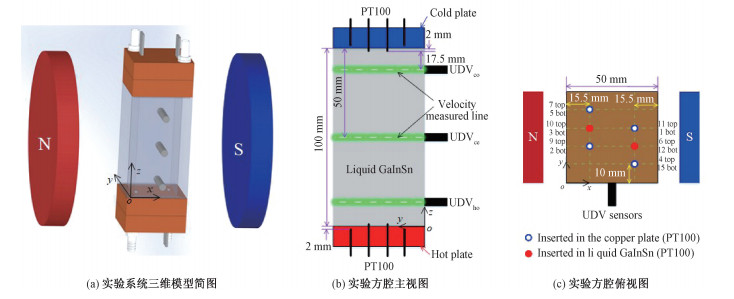
1 实验系统介绍 1.1 实验系统为开展水平磁场作用下热对流的实验特性研究,搭建了包含速度、温度测量的液态金属Rayleigh-Bénard流动实验平台,实验系统如图 1所示。
|
Download:
|
| 图 1 实验系统图 Fig. 1 Sketch of the experimental system | |
图 1(a)给出了实验系统的三维示意图,其中包含由永磁体组成的磁体,有机玻璃制成的内部长宽高分别为50 mm、50 mm和100 mm的方腔(后统称宽高比为0.5的方腔),上下铜块组成的温差系统,其中铜块内部为复杂的槽道用于通入恒定温度的水以保证整个铜板与液态金属接触的部位实现恒温边界条件。实验采用的液态金属为室温下为液态的镓铟锡合金,该流体对应的物性参数详见文献[31]。实验的磁场环境是由2块永磁体产生,通过对永磁体磁头的外形设计和外围铁芯结构的设计实现在120 mm直径、95 mm磁极宽度的圆柱体空间内产生强度为282 mT、均匀度为99.2%的磁场。由于磁头之间的间距已经为设定的最大值,本次实验仅研究了一种磁场强度对不同温差作用下的RB对流现象的影响。整个方腔的外围由导热系数较低的保温棉包裹,以最大程度实现实验段与外界环境的隔热;而开展磁场环境实验时,我们将包裹好的实验段先放入2个永磁铁所组成的磁极间,然后放置于密闭的填充保温棉的泡沫箱中进行实验。采用此种方法的主要目的是进一步降低实验系统的热损失。
1.2 测量及数据处理方法在液态金属的流动和传热特征定量测量方面,在实验方腔和铜板分别布置了用于测量速度和温度的探头。由于液态金属不透明,本实验采用超声波多普勒测速(UDV)技术对液态金属内部的速度分布进行测量。超声波探头的位置详见图 1(b),3个超声波探头分别布置于实验段靠近热/冷板(距离为17.5 mm)和实验段中心位置,用于测量沿超声波发射方向多个点位置的速度,速度测量的空间分辨率为1.1 mm,其中UDV下标co、ce和ho分别表示靠近冷(cool)端、中(centre)端和热(hot)端位置的探头。受限于实验空间和探头的长度,本次实验仅在垂直磁场方向布置了3个探头,可以获得沿y方向的液态金属流动速度,通过对3个探头获得的速度分布进行分析可以获得方腔内大尺度速度环流的流动结构特征。在温度测量方面,采用铠装式铂电阻(PT100)分别插入铜板(距离靠近液态金属的壁面2 mm)和液态金属内部(插入深度2 mm)以获得铜板的平均温度以及液态金属的温度波动特征,测温探头的详细布置信息如图 1(c)所示,其中的top表示为顶(冷)端铜板内插入的温度传感器,bot表示为底(热)端铜板内插入的温度传感器。在速度测量精度方面,选用瑞士Signal Processing SA生产的DOP3010主机并结合8 MHz的探头实现约0.1 mm/s的速度测量精度;在温度测量精度方面,选用PT100铂电阻,经过温度校准后能实现在标定温度范围10~80 ℃内0.01 ℃的测量精度。本实验中,最低测量速度为2 mm/s,实验段温度范围控制在15~35 ℃,上下铜板的最低温差为0.2 ℃,因此仪器测量的精度满足实验的要求。
通过调节连接上下铜板的恒温水浴的温度实现对冷热端的温差调节,进而改变实验对应的无量纲瑞利数。这里瑞利数(Ra)是表征浮升力和黏性力比值的一个无量纲参数,其定义为
| $R a=\alpha g \Delta T H^3 / \kappa \nu .$ | (1) |
其中:α为体积热膨胀系数,g为重力加速度,ΔT为冷热端铜板的温差,H为流体层的厚度(100 mm),ν为液态金属的运动黏度,κ为热扩散系数。
采用Chandrasekhar数(Q)表征洛伦兹力与黏性力之比,其定义式为
| $Q=H a^2=B^2 W^2 \sigma / \rho \nu.$ | (2) |
其中:B为磁场的强度,Ha为哈特曼数,σ为液态金属的导电率,ρ为流体的密度,W为方腔的宽度。
根据热湍流的相关性质可知,对于具有一定温差的对流腔,其所实现的理论对流速度Ufree可按下式进行计算
| $U_{\text {free }}=\sqrt{g \alpha H \Delta T} .$ | (3) |
对实验数据处理时,采用Ufree对测量得到的速度进行无量纲化。
相应对流时间定义为
| $t_{\text {free }}=\sqrt{H / g \alpha \Delta T} .$ | (4) |
本实验通过调节冷端和热端的温差实现Ra数在5.3×105~3.2×106之间变动,对应磁场下的Q数为3.09×105。
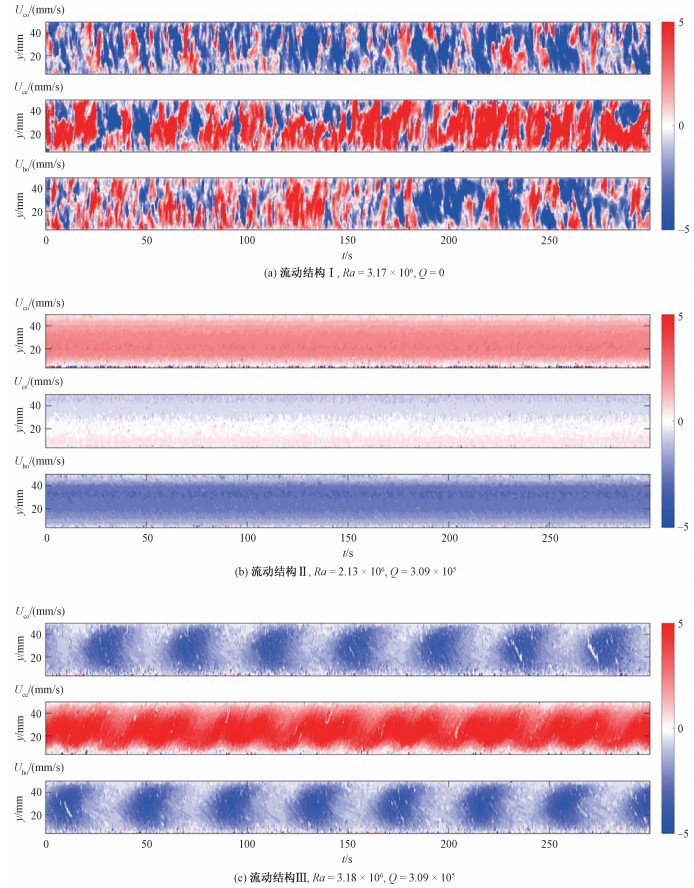
2 实验结果与讨论 2.1 典型流动结构基于超声波多普勒测速方法,实验中获得不同工况下上、中、下3个测量位置的速度随时间变化特性,这里给出3种典型工况下的速度时空分布云图,如图 2所示。图 2(a)为无磁场的实验结果,图 2(b)和2(c)为固定磁场强度、变化瑞利数的实验结果。从整体实验结果可以看出,无磁场环境下速度变化呈现无序的状态,而水平磁场存在下(磁场方向与温差方向垂直)速度的变化较为规则,出现稳定的流动结构和周期性变化的流动结构。
|
Download:
|
| 图 2 3种典型流动结构对应的速度时空分布云图 Fig. 2 The spatio-temporal velocity distribution of three typical flow patterns | |
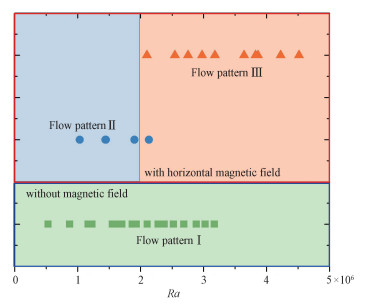
从图 2(a)可以看出,沿着探头方向测量得到的速度在时间和空间方向均正负交替出现,具有较强的波动,而且在同一时刻不同探头测量得到的速度也明显不同,体现出热湍流的主要特征。对于相近Ra数,当水平磁场作用时(对应Q = 3.09 × 105),速度分布的时空图出现了明显的变化:上下探头测量得到的速度均为负值,速度的幅值呈现周期性的波动,且波动呈现一定的相位差;中心位置的探头测量得到的速度始终为正,且与上下探头测量的速度具有类似的波动特征,这种速度分布类似于沿着温度梯度方向的对涡结构。而在不改变磁场强度、减小Ra数时,流动又转变成另外一种形态,此时,从速度云图可以明显看出:对应的速度幅值明显减小,速度的波动性也明显减弱;上下探头测量得到的速度方向相反,中间探头得到的速度接近于零,此时对应的流动形态类似于在整个实验方腔内形成稳定的大涡结构。而对于本实验参数范围内的其他工况,流动的大体形态均与这3种典型的流态类似,图 3给出了本实验参数范围内3种流动形态产生的对应Ra数区间。实验参数范围无磁场情形对应的是与图 2(a)类似的流动形态Ⅰ,而在固定磁场强度环境下,流动呈现出2种不同的流动形态,Ra小于2×106对应的流动形态Ⅱ(对应图 2(b))以及Ra大于2.5×106对应的流动形态Ⅲ(对应图 2(c)),而在Ra为2 × 106~2.5×106的范围内,流动形态Ⅱ和流动形态Ⅲ均可在实验中出现。虽然本实验参数范围内的流动基本符合这3种流动形态,但在同一流动形态范围内,不同Ra条件下对应的流动细节有些许差异,其差异对应的详细特征以及解释将在后文阐述。
|
Download:
|
| 图 3 3种典型流动结构相图 Fig. 3 The phase diagram of three typical flow patterns | |
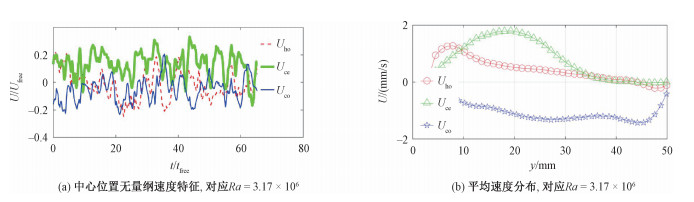
首先分析无磁场对应的详细流动特征。图 4(a)给出了典型工况实验方腔上、中、下测量线位置的中心点位置(y=25 mm)无量纲速度随时间的波动特性,其中速度采用公式(3)进行无量纲化。从图中可以看出,3个监测点的速度波动幅值基本保持一致,而中间测点位置无量纲速度以正为主,冷端和热端测量点的速度呈现正负交替的变化特征。进一步对测量速度做时间平均处理,将该工况下的结果绘制于图 4(b)。从图中可看出,沿着探头测量方向,速度的整体变化较为平缓,且平均后热端和中心位置的速度为正,靠近冷端的速度为负。结合图 4(a)和4(b)发现,无磁场环境下液态金属所形成的流动虽然在时间上具有较为明显的波动特性,但也具有一定的倾向性,即速度整体会呈现正向和负向。
|
Download:
|
| 图 4 无磁场下速度分布特性 Fig. 4 The fluctuation of velocity in non-magnetic | |
为进一步分析不同工况下速度分布的趋势,对3个探头的测量速度结果进行统计分析,计算了速度的概率密度分布,并将3种典型工况的速度概率密度分布结果绘制于图 5。从图 5(a)可以看出,速度整体呈现高斯分布,但靠近热端的速度以负值为主,靠近冷端的速度以正值为主,中心位置的速度以负值为主;然而当Ra数产生较小变化时整个流动结构产生明显的反转,如图 5(b)所示。进一步增加Ra数,3个测量位置速度概率密度分布的整体形态基本保持不变,但曲线的幅度变大且更陡峭。速度的这种类高斯分布特征表明无磁场下流动具有典型的湍流特征。同时,无磁场环境下不同工况所产生的流动统计速度方向相反的现象可能主要是由于热对流的初始条件引起的。更多定量的流动结构变化特征可能需要通过借助数值模拟的手段分析整个方腔内的速度分布来实现。
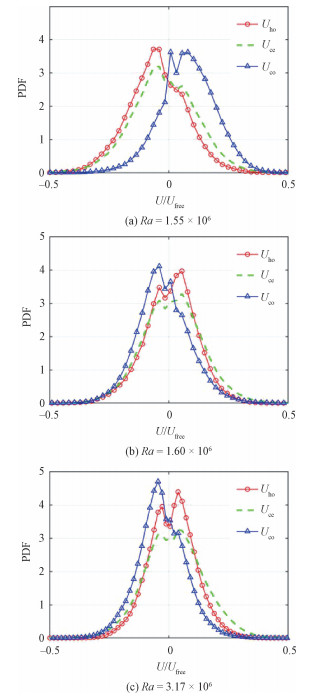
|
Download:
|
| 图 5 速度概率密度分布 Fig. 5 The probability density function of velocity | |
对于热湍流而言,浮升力主导的热对流一般满足Bolgiano-Obukhov(BO)标定率,即-11/5,而惯性主导的流动一般满足Kolmogorov-Obukhov(KO)标定律,即-5/3[35]。随后,对3个不同Ra数工况下UDV测量得到的实验段几何中心位置的速度进行频谱分析,以验证本实验条件下液态金属热对流的湍流特性,相关结果如图 6所示。从图中可以看出,3种不同Ra数条件下速度衰减均与KO标定率接近,表明液态金属在本实验的Ra区间内满足惯性对流的基本特征。
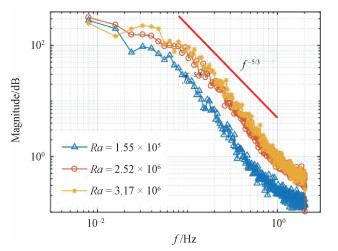
|
Download:
|
| 图 6 速度能谱图 Fig. 6 The energy spectrum diagram of velocity | |
磁场环境下,运动的液态金属会因为切割磁感线而产生感应电流,感应电流与磁场相互作用形成与运动方向相反的洛伦兹力。这种体积力的作用极大地改变了液态金属内部的流场结构和相应的传热特性。本节主要通过对实验获得的速度数据进行分析,深入理解磁场对液态金属热对流的流动结构的影响。
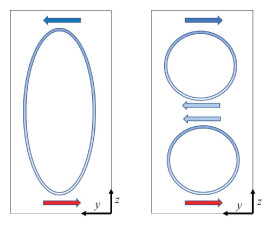
图 7给出水平均匀磁场作用下3个探头的测量线中心位置速度无量纲化后随时间的变化特征。相比无磁场的工况(图 4 (a)),磁场的存在使得无量纲速度的波动幅度明显减小,当Q/Ra较大(图 7(a),对应流动结构Ⅱ)时,即洛伦兹力占主导的情形,此时3个UDV探头速度测量线的中心位置速度随时间的波动幅值相比无磁场工况明显减小,且呈现非常有规律的特征:靠近热端的流体速度始终为正,靠近冷端的流体速度始终为负,且幅值大小与热端保持一致,几何中心位置的速度在零附近波动,结合图 2(b)和8(a)可以非常清晰判断出此时对应的流动形态为典型的稳定单涡胞结构,流动示意图如图 9(a)所示。这种稳定单涡胞运动的产生主要是由于水平磁场的作用极大削弱了沿磁力线方向的速度梯度,进而使得涡胞的运动轴线与磁力线平行,涡胞运动形态稳定。
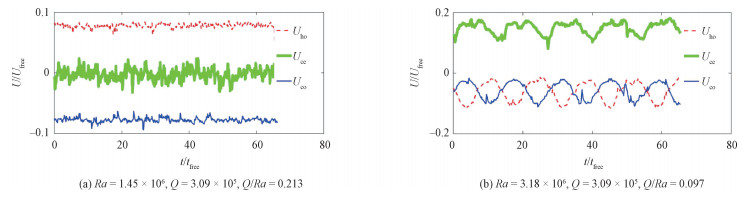
|
Download:
|
| 图 7 速度波动图 Fig. 7 Velocity fluctuations | |
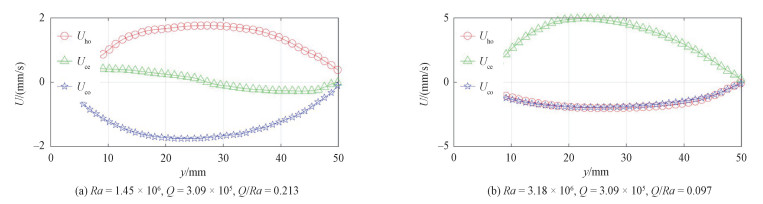
|
Download:
|
| 图 8 平均速度分布图 Fig. 8 Averaged velocity distribution | |
|
Download:
|
| 图 9 磁场作用下2种典型的流动结构示意图 Fig. 9 Typical two flow structures under the influence of magnetic field | |
进一步对几何中心点的速度进行频谱分析可以发现(图 10),当Q/Ra不为零,即存在磁场时,整个能谱曲线的幅值明显减小,且随着Q/Ra的增大,对应的幅值进一步减小。而由于本实验的磁场强度为固定值,且其幅值较小,磁场的存在虽然改变了能量谱的整体幅值大小,但并没有改变能量衰减的斜率,在高频位置仍与无磁场下惯性主导的流动特征一致,即符合-5/3的KO标定律。当Q/Ra较小(图 7(b),对应流动结构Ⅲ)时,磁场使得无量纲速度随时间的变化呈现出类似于三角函数的周期性变化特征,且靠近冷端的流体中心位置速度与靠近热端的流体中心位置速度方向相同,但幅值的相位差刚好为90°,说明在方腔内的热端和冷端存在明显的脉动羽流结构,且热端速度极大值的出现与冷端速度极小值的出现具有较强的关联性,而中心测量位置速度的变化频率接近于上下端速度交替变化频率的1/2。结合图 8(b)的3个探头测量得到速度的时间平均分布结果可以初步认为此时在方腔内的流动结构为在重力方向分布的2个交替振荡涡胞结构,为典型的双涡胞振荡形态,流动结构示意图如图 9(b)所示。进一步地,对方腔内几何中心的速度测量结果进行FFT变化,并绘制在能谱图上。从图 10可以看出,此时的能谱曲线在低频位置存在2个峰值点,对应的频率分别为0.023和0.046。这2个频率值分别与图 7(b)中的中心位置速度变化频率和上下段速度峰值交替变化频率完全对应。这说明,冷端附近流体的变化和热端附近流体的变化在中心位置进行组合,形成一个除主频外的2倍高频变化特征。这也进一步验证此工况下对应的流动形态为双涡胞振荡结构。然而,受限于超声波测速法在空间测量方面的局限性,后期可通过直接数值模拟的方法进一步对这种双涡振荡形态流动结构进行精细的研究,以深入解释当Q/Ra增加时涡胞数目增加的原因。

|
Download:
|
| 图 10 速度能谱图 Fig. 10 The energy spectrum diagram of velocity | |
本文通过实验研究了固定水平磁场强度影响下液态镓铟锡在宽高比为0.5方腔内Rayleigh-Bénard对流特性,采用超声波多普勒测速技术获得方腔内3个不同位置的速度分布,并结合温度测量对不同工况下液态金属的流动结构特征进行详细分析,具体结论如下:
1) 通过对速度的分析得到了有/无水平磁场存在下的3种典型流动结构,并将本文的所有实验工况绘制在相图上,无磁场时流动始终处于流动结构Ⅰ,而磁场存在时存在流动结构Ⅱ和流动结构Ⅲ,2种流动的转变临界Ra数区间约为2.0×106~2.5×106。
2) 无磁场情形下,液态金属的热对流流动结构Ⅰ的基本特征为:3个不同测量位置的速度波动幅值较大,且与平均流动同量级;不同工况下系统的大尺度环流会存在相反的旋转方向;速度能谱处在由惯性主导对流的-5/3标定律区间。
3) 水平磁场存在时,液态金属热对流流动结构Ⅱ的基本特征为:此时洛伦兹力占主导地位,冷、热端附近的流体运动速度大小相等,方向相反,且中心位置的流动速度分布接近正弦分布的特征;3个探头测量得到的速度随时间的脉动均较小,流动为稳定的大涡胞结构。
4) 水平磁场存在时,液态金属热对流流动结构Ⅲ的基本特征为:此时洛伦兹力和惯性力共同作用,冷、热端附近的流体速度方向相同,大小呈现此消彼长的变化趋势,且这一变化频率为中心位置流体速度变化频率的2倍,这一速度周期性变化的频率与频谱图上所获得的主频信息保持一致。
| [1] |
Brent A D, Voller V R, Reid K J. Enthalpy-porosity technique for modeling convection-diffusion phase change: application to the melting of a pure metal[J]. Numerical Heat Transfer, 1988, 13(3): 297-318. Doi:10.1080/10407788808913615 |
| [2] |
Hartmann D L, Moy L A, Fu Q. Tropical convection and the energy balance at the top of the atmosphere[J]. Journal of Climate, 2001, 14(24): 4495-4511. Doi:10.1175/1520-0442(2001)014<4495:TCATEB>2.0.CO;2 |
| [3] |
McKenzie D P, Roberts J M, Weiss N O. Convection in the earth's mantle: towards a numerical simulation[J]. Journal of Fluid Mechanics, 1974, 62(3): 465. Doi:10.1017/S0022112074000784 |
| [4] |
Bénard H. Les tourbillons cellulaires dans une nappe liquid[J]. Revue Générale des Sciences Pures et Appliquées, 1900, 11: 1261-1271. |
| [5] |
Rayleigh L. LIX. On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1916, 32(192): 529-546. Doi:10.1080/14786441608635602 |
| [6] |
Chandrasekhar S. Hydrodynamic and hydromagnetic stability[M]. New York: Oxford University Press, 1961.
|
| [7] |
Oberbeck A. Ueber Die Wärmeleitung der Flüssigkeiten Bei berücksichtigung der strömungen infolge von temperaturdifferenzen[J]. Annalen Der Physik Und Chemie, 1879, 243(6): 271-292. Doi:10.1002/andp.18792430606 |
| [8] |
Grossmann S, Lohse D. Scaling in thermal convection: a unifying theory[J]. Journal of Fluid Mechanics, 2000, 407: 27-56. Doi:10.1017/50022112099007545 |
| [9] |
Grossmann S, Lohse D. Thermal convection for large Prandtl numbers[J]. Physical Review Letters, 2001, 86(15): 3316-3319. Doi:10.1103/PhysRevLett.86.3316 |
| [10] |
Grossmann S, Lohse D. Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection[J]. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 2002, 66(1 pt 2): 016305. Doi:10.1103/PhysRevE.66.016305 |
| [11] |
Zhou Q, Xia K Q. Physical and geometrical properties of thermal plumes in turbulent Rayleigh-Bénard convection[J]. New Journal of Physics, 2010, 12(7): 075006. Doi:10.1088/1367-2630/12/7/075006 |
| [12] |
周全, 夏克青. Rayleigh-Bénard湍流热对流研究的进展、现状及展望[J]. 力学进展, 2012, 42(3): 231-251. Doi:10.6052/1000-0992/11-163 |
| [13] |
Sun C, Xia K Q. Scaling of the Reynolds number in turbulent thermal convection[J]. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 2005, 72(6 Pt 2): 067302. Doi:10.1103/PhysRevE.72.067302 |
| [14] |
Yanagisawa T, Yamagishi Y, Hamano Y, et al. Structure of large-scale flows and their oscillation in the thermal convection of liquid gallium[J]. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 2010, 82(1 Pt 2): 016320. Doi:10.1103/PhysRevE.82.016320 |
| [15] |
Busse F H, Clever R M. Stability of convection rolls in the presence of a vertical magnetic field[J]. The Physics of Fluids, 1982, 25(6): 931-935. Doi:10.1063/1.863845 |
| [16] |
荣升. 导电流体热对流中磁场的致稳作用[J]. 力学学报, 1993, 25(6): 658-664. |
| [17] |
Busse F H. The oscillatory instability of convection rolls in a low Prandtl number fluid[J]. Journal of Fluid Mechanics, 1972, 52(1): 97-112. Doi:10.1017/S0022112072002988 |
| [18] |
Clever R M, Busse F H. Transition to time-dependent convection[J]. Journal of Fluid Mechanics, 1974, 65(4): 625-645. Doi:10.1017/S0022112074001571 |
| [19] |
Fauve S, Laroche C, Libchaber A, et al. Effect of a horizontal magnetic field on convective instabilities in mercury[J]. Journal De Physique Lettres, 1981, 42(21): 455-457. Doi:10.1051/jphyslet:019810042021045500 |
| [20] |
Libchaber A, Fauve S, Laroche C. Two-parameter study of the routes to chaos[J]. Physica D: Nonlinear Phenomena, 1983, 7(1/2/3): 73-84. Doi:10.1016/0167-2789(83)90117-3 |
| [21] |
Lehnert B, Little N C. Experiments on the effect of inhomogeneity and obliquity of a magnetic field in inhibiting convection[J]. Tellus, 1957, 9(1): 97-103. Doi:10.3402/tellusa.v9il.9063 |
| [22] |
Yu X X, Zhang J, Ni M J. Numerical simulation of the Rayleigh-Bénard convection under the influence of magnetic fields[J]. International Journal of Heat and Mass Transfer, 2018, 120: 1118-1131. Doi:10.1016/j.ijheatmasstransfer.2017.11.151 |
| [23] |
Horanyi S, Krebs L, Müller U. Turbulent Rayleigh-Bénard convection in low Prandtl-number fluids[J]. International Journal of Heat and Mass Transfer, 1999, 42(21): 3983-4003. Doi:10.1016/s0017-9310(99)00059-9 |
| [24] |
Burr U, Müller U. Rayleigh-Bénard convection in liquid metal layers under the influence of a vertical magnetic field[J]. Physics of Fluids, 2001, 13(11): 3247-3257. Doi:10.1063/1.1404385 |
| [25] |
Aurnou J M, Olson P L. Experiments on Rayleigh-Bénard convection, magnetoconvection and rotating magnetoconvection in liquid gallium[J]. Journal of Fluid Mechanics, 2001, 430: 283-307. |
| [26] |
Takeshita T, Segawa T, Glazier J A, et al. Thermal turbulence in mercury[J]. Physical Review Letters, 1996, 76(9): 1465-1468. Doi:10.1103/PhysRevLett.76.1465 |
| [27] |
周仲凯, 王增辉, 陈然. 强磁场下液态金属在竖直平板外的自由对流换热[J]. 中国科学院大学学报, 2020, 37(1): 13-19. Doi:10.7523/j.issn.2095-6134.2020.01.003 |
| [28] |
Yanagisawa T, Yamagishi Y, Hamano Y, et al. Detailed investigation of thermal convection in a liquid metal under a horizontal magnetic field: Suppression of oscillatory flow observed by velocity profiles[J]. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 2010, 82(5 pt 2): 056306. Doi:10.1103/PhysRevE.82.056306 |
| [29] |
Yanagisawa T, Yamagishi Y, Hamano Y, et al. Spontaneous flow reversals in Rayleigh-Bénard convection of a liquid metal[J]. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 83(3 Pt 2): 036307. Doi:10.1103/PhyRevE.83.036307 |
| [30] |
Vogt T, Horn S, Grannan A M, et al. Jump rope vortex in liquid metal convection[J]. Proceedings of the National Academy of Sciences of the United States of America, 2018, 115(50): 12674-12679. Doi:10.1073/pnas.1812260115 |
| [31] |
Vogt T, Ishimi W, Yanagisawa T, et al. Transition between quasi-two-dimensional and three-dimensional Rayleigh-Bénard convection in a horizontal magnetic field[J]. Physical Review Fluids, 2018, 3: 013503. Doi:10.1103/physrevfluids.3.013503 |
| [32] |
Akashi M, Yanagisawa T, Tasaka Y, et al. Transition from convection rolls to large-scale cellular structures in turbulent Rayleigh-Bénard convection in a liquid metal layer[J]. Physical Review Fluids, 2019, 4(3): 033501. Doi:10.1103/PhysRevFluids.4.033501 |
| [33] |
Zürner T, Schindler F, Vogt T, et al. Combined measurement of velocity and temperature in liquid metal convection[J]. Journal of Fluid Mechanics, 2019, 876: 1108-1128. Doi:10.1017/jfm2019.556 |
| [34] |
Lim Z L, Chong K L, Ding G Y, et al. Quasistatic magnetoconvection: Heat transport enhancement and boundary layer crossing[J]. Journal of Fluid Mechanics, 2019, 870: 519-542. Doi:10.1017/jfm.2019.232 |
| [35] |
Shang X D, Xia K Q. Scaling of the velocity power spectra in turbulent thermal convection[J]. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 2001, 64(6 Pt 2): 065301. Doi:10.1103/PhysRevE.64.065301 |
 2023, Vol. 40
2023, Vol. 40 


