2. 上海科技大学, 上海 201210;
3. 中国科学院大学, 北京 100049
2. ShanghaiTech University, Shanghai 201210, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
在传统的蜂窝无线通信系统中,为优化时频资源的分配和选取合适的调制编码方式,通常采用导频的方法对无线信道进行评估。这要求系统不断传输导频信号对信道进行测量;另一方面,5G无线通信系统采用了大规模多输入多输出(massive multiple input multiple output,MIMO)技术[1]。MIMO基站配备数十甚至数百个天线,通过多根天线实现多发多收,在不增加频谱资源和天线发射功率的情况下,成倍地提高系统信道容量[2-4]。但是天线数目的大规模增加也意味着通过导频的方式进行信道测量的复杂度大幅增加[5-6],因此基于导频的信道估计在采用大规模MIMO的系统中面临极大的挑战。
一种可能缓解上述问题的方法是采用信道预测,对时间序列分析,即通过某一时刻之前一段连续时间序列的信道数据,预测之后时间序列的信道特征。传统的时间序列分析方法如ARMA模型(autoregressive moving average model)[7],实际的时间序列往往是带有非线性的、非平稳、不规则和混沌的特性,这使得传统的统计学方法在时间序列的实际应用中很难准确地进行分析和预测。ARMA本质上只能捕捉线性关系,不能捕捉非线性关系,而且ARMA方法需要提前估计阶数,不能很好地适应时间序列模型的复杂变化。
文献研究表明,相空间重构理论预测时间序列常用于自然灾害、风力发电、股票等的预测[8-10],很少被用在小尺度信道衰落的预测中。本文提出一种运用混沌理论处理时间序列的方法,通过对历史信道数据构成的时间序列进行相空间重构,结合机器学习预测信道数据。在文献[11]中,作者提出一种混沌通信中FIR信道盲辨识的自适应算法,利用混沌信号的短时可预测性来均衡混沌通信系统的信道失真。文献[12]提出利用极大极小概率机选择学习样本的最佳嵌入维数后,利用极大极小概率机进行非线性预测,得到时间序列的预测值。然而文献[11-12]都没有基于相空间重构方法对MIMO信道数据构成的相空间相关参数展开深入研究。本文使用时间序列对单变量进行预测,并与神经网络预测结合,以提升预测稳定性。利用时间的相关性,文献[13]中AR将时变信道的脉冲响应建模为自回归过程;文献[14]采用ARMA模型预测信道,并根据预测的信道生成PCA中的压缩矩阵,通过过去CSI来预测未来CSI;文献[15]提出ARMA-mmWave信道预测模型, 有效提高了吞吐量。虽然文献[13-15]提出的ARMA方法预测信道数据,但都不涉及3D MIMO信道模型,本文提出的相空间重构结合神经网络的预测方法是针对3D MIMO无线信道的,能够快速、准确地预测信道参数,并用实测数据验证方法的可行性,对3D MIMO无线信道预测的研究有一定的贡献。
本文深入研究MIMO信道数据构成的相空间的相关参数,并根据分析输出的最优参数对信道时间序列数据进行相空间重构,结合神经网络对信道系数和高斯信道容量进行预测。与传统ARMA方法相比,本文所提出的方法适用于非线性的情形,在系统变化时可以学习到高阶非线性特征。具体贡献包括:1)通过大量实验数据分析3D信道数据的最大Lyapunov指数的特征,证实MIMO三维信道系数构成的时间序列具有混沌性;2)在无线传播环境保持基本不变的前提下,通过实验和分析,发现基于MIMO信道系数计算的吸引子维数的经验概率分布接近正态分布以及延迟时间为固定值,并将2个参数值作为先验参数设定,在动态的信道系数预测时,不再实时求解2个参数,大大减少了对动态信号进行分析处理的工作量;3)根据设定的先验参数重构相空间,再用机器学习实现MIMO信道系数及其高斯信道容量的预测,从而实现多天线相关性、信道容量等基本MIMO信道特征的准确预测。并且因已有先验参数(嵌入维数和延迟时间),使用小样本即可实现BP神经网络的自适应训练,大大节约训练时间。
实验结果表明,采用文中的实验设置,预测高斯信道容量的平均误差最小为5.91%,同时预测效率相比传统的ARMA方法提升6倍左右。最后,采用在某市区场景下测试的真实信道数据验证相空间重构方法的有效性,基于实测信道数据的高斯信道容量的平均预测误差最小为0.91%。
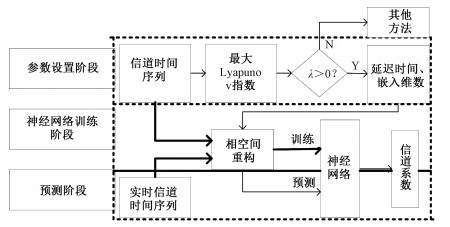
1 系统模型整体分析方法示意图如图 1所示。第一部分先设置参数,根据最大Lyapunov指数判断时间序列是否具有混沌性,这是关键的一步,然后求重构相空间的2个参数:嵌入维数m和延迟时间τ,并将这2个参数设置为先验参数;第二部分训练神经网络,在相空间重构之后通过训练BP神经网络得到训练模型;最后一部分是预测,基于实时训练样本重构相空间后通过神经网络预测信道系数及其高斯信道容量。
|
Download:
|
| 图 1 整体分析方法示意图 Fig. 1 Illustration of overall analysis method | |
本文是在以下条件下进行研究的,接收端反射点(或散射点等影响传播环境的模型要素)不变,用户低速移动下在短时间内(即在预测的时间内,一般为百毫秒)沿着固定路线移动,且用户的分布服从均匀随机分布。文献[16-17]对无线信道模型的生成进行了研究,本文信道模型为3GPP中的标准3D-UMa模型。由于3GPP标准化的工作,以及各大设备供应商、运营商的共同努力,目前5G实际生产、测试、网络规划、优化等应用场景中基本上都是采用3GPP 38.901标准模型。其频率为2 GHz, 带宽为20 MHz,基站的天线阵列是面阵天线,定向天线,天线单元的辐射方向图参照3GPP TR 38.901 7.3 Antenna modelling,每行16根天线单元,一共4行,垂直方向天线单元间隔为0.8个波长,水平方向天线单元间隔为0.5个波长;用户的天线阵列是线阵天线,天线单元间隔为0.5个波长。天线的极化方式为双极化。本文的模型是标准的3GPP 3D-UMa模型,其他参数可参考3GPP TR 38.901。
本文使用的MIMO信道数据基于3D-UMa模型生成,数据结构是一个9维的信道系数矩阵。其中第4维是接收端用户的天线数,一共10个用户,每个用户分配2根接收天线。第8维是发射端基站的天线数,本文使用的数据有8根发射天线。第9维是TTI(transmission time interval,TTI),1个TTI对应1 ms时长。信道数据为复数形式的频域信道数据,数据一共有10组,分别在不同用户速度下采集,用户移动速度(单位:km/h)分别设置为:{5, 25, 30, 50, 60, 70, 75, 80, 90, 100}。
2 相空间重构的参数设置相空间重构技术用于恢复混沌系统的相空间,相当于恢复混沌系统。混沌时间序列的判定、训练和预测都是在这个重构的相空间中进行的,因此相空间的重构就是混沌时间序列研究的关键,而相空间重构的2个参数又是重构相空间的关键。混沌时间序列的预测方法与传统的预测方法不同,混沌理论的应用很大程度上依赖Takens提出的相空间重构方法[18],相空间重构是来自于混沌动力学的一种预测方法,可避免人为造成的主观性,提高预测的精度。本文将基于相空间重构方法研究MIMO信道数据构成的相空间重构参数的设置方法,并利用先验参数进行信道容量的预测,同时,基于相空间重构方法预测信道存在的参数在线寻优问题,提出一种应用射线传播模型特征快速预测最优相空间参数的配置方法,然后通过延迟时间和嵌入维数参数确定的信道数据的时间序列建立相空间重构,再结合机器学习对信道数据预测。
2.1 分析MIMO信道时间序列的混沌特征混沌运动对初值条件极为敏感,2个很相近的初值所产生的轨道,随时间推移按指数方式分离。Lyapunov指数就是定量描述这一现象的量。将迭代次数取平均,平均每次迭代所引起的指数分离中的指数为λ,λ < 0意味着相邻点最终要靠拢合并成一点,这对应于稳定的不动点和周期运动,若λ > 0,则意味着相邻点最终要分离,这对应于轨道的局部不稳定,长时间行为对初始条件敏感,运动呈混沌状态。
确定信道数据的时间序列具有混沌性是进行相空间重构的基础,Lyapunov指数是区分系统混沌状态或非混沌状态的最直接特征量之一,可以反映系统小扰动随时间的发散或收敛[19]。如果信号的最大Lyapunov指数大于零,则该系统是混沌的。由于获得的信道数据是有限长度的,所以本文用小数据量法计算最大Lyapunov指数。
对序列{x(i), i=1, 2, …, N}进行傅里叶变换计算时间序列的平均周期,得到延迟时间和嵌入维数之后重构相空间,相点用下式表示
| $ \begin{gathered} \boldsymbol{X}(i)=[x(i), x(i+\tau), x(i+2 \tau), \cdots, \\ x(i+(m-1) \tau)], i=1, 2, \cdots, M . \end{gathered} $ | (1) |
对相空间每个相点Xj找到它的最近邻点Xk并限制短暂分离,即下式所示
| $ d_j(0)=\min \limits_k\left\|\boldsymbol{X}_j-\boldsymbol{X}_k\right\|, |j-k|>P . $ | (2) |
对相空间每个相点Xj计算出该邻点对的i个离散时间步后的距离dj(i)和y(i), 如下式
| $ \begin{gathered} d_j(i)=\left|\boldsymbol{X}_{j+i}-\boldsymbol{X}_{k+i}\right|, i=1, 2, \cdots, \\ \min (M-j, M-k) . \end{gathered} $ | (3) |
| $ y(i)=\frac{1}{q(t)} \sum\limits_{j=1}^q \ln d_j(i). $ | (4) |
q是非零dj(i)的数目,并用最小二乘法对式(4)做回归直线,直线的斜率就是最大Lyapunov指数。式(1)中的τ为延迟时间,M为相点个数,m为嵌入维数。
本文利用最小数据量法计算,与其他方法相比,计算结果可靠, 所用数据较少,对相空间的嵌入维数、延迟时间具有鲁棒性。经过大量数据分析,同一射线数据下不同用户速度下的最大Lyapunov指数λ都大于零,信道数据时间序列是混沌的。
2.2 相空间重构参数:延迟时间参数嵌入维数和延迟时间是重构相空间的基本输入参数。一般用自相关函数法(autocorrelation function,ACF)或互信息函数法(mutual information,MI)来确定延迟时间,若延迟太小,相轨迹互相挤压,信息显示不足;若延迟太大,会导致前后时刻变化过于剧烈,信息显示太复杂,甚至失真。ACF只测量变量之间的线性相关性,所以不一定适用于非线性系统[20],互信息的方法考虑了时间序列的非线性特征,计算结果一般优于自相关法得到的结果。文献[21]建议使用第一局部最小值,它根据概率分布而不是线性参数来测量连续点之间的一般相关性。
互信息函数可以定义为
| $ I(\tau)=\sum\limits_{i=1}^N P\left(x_i+x_{i+\tau}\right) \log _2\left[\frac{P\left(x_i, x_{i+\tau}\right)}{P\left(x_i\right) P\left(x_{i+\tau}\right)}\right] . $ | (5) |
其中:N是数据集{x1, x2, …, xN}的个数,P(xi)和P(xi+τ)分别是在时间序列{x1, x2, …, xN}和{x1+τ, x2+τ, …, xN+τ}出现的概率,P(xi, xi+τ)是xi和xi+τ出现在2个序列中的联合概率。
本文利用等间距划分空间格子的方法确定互信息函数的第一极小值,应用方便、简洁省时。因为信道矩阵系数是复数,预测时需要对实部、虚部分别进行预测,所以对实部、虚部都要求取延迟时间。经不同射线数据下得到的信道数据大量实验得到实部、虚部的延迟时间都为2个TTI,可作为先验参数设定,减少对动态信号分析的工作量。
2.3 相空间重构参数:嵌入维数选取合适的延迟时间以后,时间序列可以被重构为m维的相空间,若m太小, 不能展现复杂行为的细致结构,但若m太大,会使计算工作复杂化,同时随之引起的噪声也不可忽视。本文用Grassberger-Procaccia算法(G-P算法),即相关积分方法计算时间序列的吸引子维数d。相关积分可以用下式计算:
| $ C(r)=\frac{2}{N(N-1)} \sum\limits_{i=1}^N H\left(r-\left\|\boldsymbol{X}_i-\boldsymbol{X}_j\right\|\right) . $ | (6) |
其中,令u=r-‖Xi-Xj‖,H是阶跃函数,
| $ H(u)= \begin{cases}1, & u>0, \\ 0, & u \leqslant 0 .\end{cases} $ | (7) |
r是以Xi或Xj为中心球体的半径,‖·‖是范数,C(r)给出2个随机选择的向量在一定距离内的概率[22]。吸引子维数d与相关积分相关,如下所示:
| $ C(r) \propto r^d. $ | (8) |
由式(8)得
| $ d=\ln C(r) / \ln r. $ | (9) |
式(9)是一种线性关系,斜率为关联维数d。因为系统是混沌的,相关维数将会达到饱和值,此时关联维数等于吸引子维数,后期再根据m≥2d+1得到嵌入维数[23]。在文献[24]中,作者认为m > d足以描述系统动力学,本文根据信道容量预测的误差大小确定在信道预测时嵌入维数的选取。
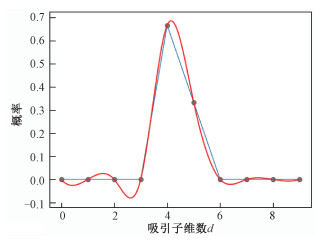
延迟时间为2个TTI, 根据式(9)求出吸引子维数,得到在3 D信道中求出的吸引子维数的经验概率分布接近于以4~5之间的值为中心的正态分布的结论。根据文献[23]吸引子维数的值向上取整,本文吸引子维数为5,并作为先验参数设定,减少后期研究其他信道数据重复求取吸引子维数的工作量。如图 2所示,为用户在不同移动速度下吸引子维数d的分布图。
|
Download:
|
| 图 2 吸引子维数的分布 Fig. 2 Distribution of attractor dimension | |
由图 2可以看出,吸引子维数可以拟合出接近正态分布的曲线图形,得出吸引子维数d=5的结论。
2.4 相空间重构设时间序列{x(i), i=1, 2, …, N},N是时间序列总长度,以延迟时间τ和嵌入维数m进行相空间重构
| $ \left[\left(\begin{array}{cccc} x(1) & x(2) & \cdots & x(M) \\ x(1+\tau) & x(2+\tau) & \cdots & x(M+\tau) \\ \vdots & \vdots & & \vdots \\ x(1+(m-1) \tau) & x(2+(m-1) \tau) & \cdots & x(M+(m-1) \tau) \end{array}\right)\right] \text {. } $ | (10) |
相空间中的相点可以表示为
| $ \begin{gathered} \boldsymbol{X}(i)=[x(i), x(i+\tau), x(i+2 \tau), \cdots, \\ x(i+(m-1) \tau)], i=1, 2, \cdots, M . \end{gathered} $ | (11) |
由矢量X构成的空间称为伪相空间(即重构的相空间),伪相空间中状态矢量X的轨迹成为伪相轨迹,伪相空间共有M=N-(m-1)τ个相点,满足嵌入维数与吸引子维数之间的m≥2d+1或m > d,这时重构的相空间与实际的动力系统具有相同的几何性质与信息性质。
3 AI赋能的相空间重构预测方法 3.1 相空间重构结合BP神经网络模型相空间重构和BP神经网络都适合解决非线性复杂的问题,本文将两者结合,发挥它们在处理信道数据时间序列这种复杂非线性问题上的有效性和互补性。相空间重构预测的模型式如下所示
| $ \begin{gathered} x(i+1+(m-1) \tau)=f[x(i) , \\ x(i+\tau), \cdots, x(i+(m-1) \tau)]. \end{gathered} $ | (12) |
其中:f(·)为待求解的映射函数。本文将通过BP神经网络代替求解映射函数f(·),通过神经网络,直接得到预测的结果。
利用相空间重构确定BP神经网络模型的输入,从而建立神经网络时间序列模型预测。一般情况下,输入层的点数为嵌入维数m,每个输入点之间的间隔为时延τ,即相空间每个维的相点X作为神经网络的输入,输出层有一个节点,为时间点x(i+1+(m-1)τ)的预测值。本文利用3层神经网络进行预测,根据经验选取BP神经网络的隐含层节点个数。由多次试验经验可得,选取隐含层节点的个数是输入层节点个数2倍时可达到理想效果,因此隐含层的节点数定为44,得到的预测数据是信道系数,信道系数是复数,因此同时预测虚部、实部,即BP神经网络的输入层的节点个数为2m, 输出层节点个数为2。
为提高准确率,本文利用窗口滑动的方法预测,W为滑动窗口的大小,输入W个相点训练模型,预测第W+1个相点的输出。窗口逐次滑动,可以预测连续时间序列的信道矩阵系数。W的设置方法后面进一步说明。
3.2 信道容量的计算信道矩阵系数组成信道矩阵H,信道容量由下式根据信道矩阵H计算得到
| $ C=\log _2\left(\operatorname{det}\left(\boldsymbol{I}_n+\operatorname{SINR}\left(\boldsymbol{H} * \boldsymbol{H}^{\mathrm{T}}\right)\right)\right). $ | (13) |
其中:
利用相对误差来度量实际信道容量与预测信道之间的差距, 如下所示
| $ e=\frac{\left|C-C^{\prime}\right|}{C} \times 100 \%. $ | (14) |
其中:e表示相对误差,C表示信道容量的实际值,C′表示预测值。
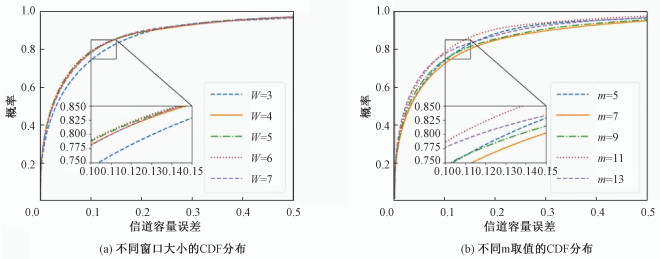
4 实验结果 4.1 嵌入维数及滑动窗口的确定求出吸引子维数d,可得到嵌入维数m,本文根据信道容量的预测误差大小确定嵌入维数m的大小以及窗口的大小。设置窗口大小W范围为3~7,画出10个用户在不同速度时各个窗口下的CDF图,如图 3(a)所示。由图可以看出,当m=11时,W=3时误差最大,窗口W越大误差越小,但增大计算窗口误差降低不明显,计算量增加,出现边际效应递减现象。因此在本文中W=5,此时误差较低,且计算量不大。
|
Download:
|
| 图 3 滑动窗口、嵌入维数的确定 Fig. 3 Determination of the sliding window and embedding dimension | |
确定窗口大小W=5之后,比较m=5和m=11时的误差CDF分布,确定m的取值。同时,测试嵌入维数取其他值时的CDF分布,如图 3(b)所示,显然m=11时CDF图在左上方,误差最小。
当m=11时的最大误差为19.46%,最小为5.91%,而m=5时,最大误差可达到28.83%。因此,在3D信道中,m≥2d+1时,重构的相空间才能够描述原相空间的动力系统。图 3(a)和3(b)确定了滑动窗口W的大小以及嵌入维数m的取值。
同时,为验证本方法对多天线的适用性,用户的移动速度为50 km/h时,接收端的每个用户天线增加到8根,发射端基站天线增加到64根进行信道预测,得到平均误差为10.5%,说明本文所运用到方法同样适用多天线的场景。
4.2 方法比较将本文提出的相空间重构结合BP神经网络方法、传统ARMA方法与BP神经网络方法预测时间序列对比。其中,BP神经网络使用3层神经网络,输入层的节点数为2m,通过4.1节的结论,输入层节点数为22,隐含层节点数定为44,输出层节点数为2。ARMA的阶数p和q针对不同用户移动速度有不同的最佳值,设置范围为1~4。
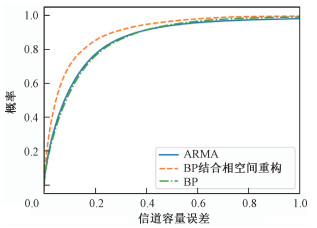
图 4是3种方法信道容量误差分布的CDF分布图,从图中可以看出,本文提出的相空间重构结合BP神经网络的方法预测方法优于传统ARMA预测方法,同时也优于仅用BP神经网络进行预测的方法。
|
Download:
|
| 图 4 3种方法误差的CDF分布 Fig. 4 CDF distribution of errors of three methods | |
使用主频为1.8 GHz、内存为16 GB的CPU硬件设备进行仿真。通过设备仿真,预测10个TTI的数据,利用BP神经结合相空间重构的方法预测所需的平均时间为5.02 s,传统ARMA方法预测需要的平均时间为31.13 s,前者比后者快6倍左右,提高了预测的时效性。本文只是进行算法有效性(精度)的验证,算法执行性能将后期进行进一步的优化。
4.3 实测数据验证本文还基于由某5G设备供应商提供的实测数据验证了BP神经网络结合相空间重构方法的有效性。测试仪器是使用某5G设备供应商自研的5G测试终端,用该终端对信道进行估计并输出实测的信道数据,通过该5G设备商开放的云平台上获取实测信道数据。所用数据来自上海市浦东新区某条城区道路上测试得到的数据,通过将接收信号做信道估计得到信道响应。实测数据样本中包含了测试终端不同移动速度、不同采样周期、不同采集地点的各类场景。
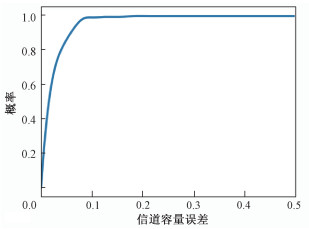
实测数据的信道矩阵是4维的,其中,第1维是间隔TTI的时间序列信号,第2维是子载波,第3维是基站天线数,第4维是用户天线数。通过3.2节所提出的方法计算信道容量,得到用户在各个实测数据的信道容量误差,误差CDF分布图如图 5所示。
|
Download:
|
| 图 5 实测数据误差的CDF分布 Fig. 5 CDF distribution of errors of measured data | |
如表 1所示,根据不同速度、不同采样周期、不同地点的实测数据,计算得到误差的平均值和方差,平均误差不到10%,比上文仿真数据的误差更小。误差的方差接近零,即各误差与平均误差接近。
|
|
表 1 实测数据平均误差和方差结果 Table 1 Results of mean error and variance of measured data |
随着速度提升,预测精度略优下降,但还能保持在较好水平,说明相空间重构法在10~40 km/h区间段对多普勒频移不太敏感,具有较好的鲁棒性。由于缺失更高速度的真实信道数据,高速条件下的真实信道数据的预测误差暂时还无法评估。
5 结论和总结本文提出混沌理论解决信道中的时间序列预测问题,在实时预测前需要在线计算延迟时间参数和嵌入维数参数,导致大量时间开销在参数探索寻优的过程,一方面严重影响了算法实时性,另一方面计算开销大,增加了成本和功耗。本文主要研究相空间重构的重要参数设置方法,在无线环境基本不变的条件下,得到最大Lyapunov指数大于零、延迟时间和嵌入维数可作为先验数值的结论。
本文提出的非线性相空间重构方法的数据采样是以延迟时间为间隔采样的,与传统线性ARAM方法以连续时间采样不同。且本文利用的BP神经网络方法是结合先验信息(嵌入维数和延迟时间)的小样本自适应的在线训练,能够拟合高阶非线性系统的特征,与传统的BP神经网络运用大量数据训练模型不同,计算开销小。此方法预测精度高,参数预置的相空间重构结合简单BP神经网络的小样本训练和预测方法,在精度上有一定的提升,最小平均误差为5%左右,且在运行效率上提升了10倍左右。
基于某5G设备供应商提供的真实MIMO信道测试数据,通过相空间重构法对信道数据进行预测,90%以上样本能够达到低于10%预测误差的水平,在低于40 km/h时速的场景中的确能够较为有效地预测信道容量,即能够正确预测天线相关性,在给定的测试数据集中可以说明相空间重构的有效性。
本文利用的神经网络是BP神经网络,后期将利用长短期记忆网络(long short-term memory,LSTM)结合相空间重构对无线信道数据进行预测,比较是否可以进一步降低高斯信道容量的预测误差。同时,计划后续进一步研究无线传播环境的几何特征对相空间重构参数的影响。此外,计划用GPU设备进行仿真,提高预测效率,减少预测所需时间。
本研究体现了信道预测的优势与必要性,信道预测能够有效减少大规模MIMO的导频测量频次、信道反馈的资源开销,对于减少测量开销、提升空口资源、降低系统综合成本有重要意义。
| [1] |
Chen C M, Volski V, van der Perre L, et al. Finite large antenna arrays for massive MIMO: characterization and system impact[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(12): 6712-6720. Doi:10.1109/TAP.2017.2754444 |
| [2] |
Hassan M E, Falou A E, Langlais C. Performance assessment of linear precoding for multi-user massive MIMO systems on a realistic 5G mmWave channel[C]//2018 IEEE Middle East and North Africa Communications Conference (MENACOMM). April 18-20, 2018, Jounieh, Lebanon. IEEE, 2018: 1-5. DOI: 10.1109/MENACOMM.2018.8371025.
|
| [3] |
Gao Y, Vinck H, Kaiser T. Massive MIMO antenna selection: switching architectures, capacity bounds, and optimal antenna selection algorithms[J]. IEEE Transactions on Signal Processing, 2018, 66(5): 1346-1360. Doi:10.1109/TSP.2017.2786220 |
| [4] |
Björnson E, Hoydis J, Sanguinetti L. Massive MIMO has unlimited capacity[J]. IEEE Transactions on Wireless Communications, 2018, 17(1): 574-590. Doi:10.1109/TWC.2017.2768423 |
| [5] |
Duel-Hallen A. Fading channel prediction for mobile radio adaptive transmission systems[J]. Proceedings of the IEEE, 2007, 95(12): 2299-2313. Doi:10.1109/JPRDC.2007.904443 |
| [6] |
Zhao J W, Xie H X, Gao F F, et al. Time varying channel tracking with spatial and temporal BEM for massive MIMO systems[J]. IEEE Transactions on Wireless Communications, 2018, 17(8): 5653-5666. Doi:10.1109/TWC.2018.2848259 |
| [7] |
He P, Yuan Y, Liu G. Web services quality prediction based on multivariate time series analysis[C]//2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS), November 23-25, 2018, Beijing, China. IEEE, 2018: 881-884. DOI: 10.1109/ICSESS.2018.8663771.
|
| [8] |
Miao T. Research of regional drought forecasting based on phase space reconstruction and wavelet neural network model[C]//2018 7th International Conference on Agro-geoinformatics (Agro-geoinformatics). August 6-9, 2018, Hangzhou, China. IEEE, 2018: 1-4. DOI: 10.1109/Agro-Geoinformatics.2018.8475999.
|
| [9] |
Han Y J, Liu J. The online forecasting research of short-term wind speed and power generation at wind farm based on phase space reconstruction[C]//2015 Seventh International Conference on Measuring Technology and Mechatronics Automation. June 13-14, 2015, Nanchang, China. IEEE, 2015: 1234-1237. DOI: 10.1109/ICMTMA.2015.300.
|
| [10] |
Guo Z Q, Chen L J, Liu P. Short-term stock forecasting based on phase space reconstruction and cluster analysis[C]//2019 11th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC). August 24-25, 2019, Hangzhou, China. IEEE, 2019, 2: 50-53. DOI: 10.1109/IHMSC.2019.10107.
|
| [11] |
Wang B Y, Zheng W X. Blind adaptive channel identification/equalization in chaotic communications by using nonlinear prediction technique[C]//Proceedings 7th International Conference on Signal Processing, 2014. Proceedings. ICSP ' 04.2004. August 31-September 4, 2004, Beijing, China. IEEE, 2004: 372-375. DOI: 10.1109/ICDSP.2004.1452659.
|
| [12] |
Zhou Y T, Wang R, Xia K W. Nonlinear prediction of fast fading channel based on minimax probability machine[C]//2011 6th IEEE Conference on Industrial Electronics and Applications. June 21-23, 2011, Beijing, China. IEEE, 2011: 451-454. DOI: 10.1109/ICIEA.2011.5975626.
|
| [13] |
Jiang W, Schotten H D. A comparison of wireless channel predictors: artificial intelligence versus Kalman filter[C]//ICC 2019—2019 IEEE International Conference on Communications (ICC). May 20-24, 2019, Shanghai, China. IEEE, 2019: 1-6. DOI: 10.1109/ICC.2019.8761308.
|
| [14] |
Nagashima R, Ohtsuki T, Jiang W J, et al. Channel prediction for massive MIMO with channel compression based on principal component analysis[C]//2016 IEEE 27th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC). September 4-8, 2016, Valencia, Spain. IEEE, 2016: 1-6. DOI: 10.1109/PIMRC.2016.7794949.
|
| [15] |
Gu S S, Jiao J, Huang Z X, et al. ARMA-based adaptive coding transmission over millimeter-wave channel for integrated satellite-terrestrial networks[J]. IEEE Access, 2018, 6: 21635-21645. Doi:10.1109/ACCESS.2018.2825256 |
| [16] |
Yang Y, Li Y, Zhang W X, et al. Generative-adversarial-network-based wireless channel modeling: challenges and opportunities[J]. IEEE Communications Magazine, 2019, 57(3): 22-27. Doi:10.1109/MCOM.2019.1800635 |
| [17] |
Huang J, Wang C X, Bai L, et al. A big data enabled channel model for 5G wireless communication systems[J]. IEEE Transactions on Big Data, 2020, 6(2): 211-222. Doi:10.1109/TBDATA.2018.2884489 |
| [18] |
Abarbanel H D I, Brown R, Kadtke J B. Prediction in chaotic nonlinear systems: methods for time series with broadband Fourier spectra[J]. Physical Review A, 1990, 41(4): 1782. |
| [19] |
Rosenstein M T, Collins J J, de Luca C J. A practical method for calculating largest Lyapunov exponents from small data sets[J]. Physica D: Nonlinear Phenomena, 1993, 65(1/2): 117-134. Doi:10.1016/0167-2789(93)90009-P |
| [20] |
Abarbanel H D I, Brown R, Sidorowich J J, et al. The analysis of observed chaotic data in physical systems[J]. Reviews of Modern Physics, 1993, 65(4): 1331-1392. Doi:10.1103/REVMODPHYS.65.1331 |
| [21] |
Fraser A M, Swinney H L. Independent coordinates for strange attractors from mutual information[J]. Physical Review. A, General Physics, 1986, 33(2): 1134-1140. Doi:10.1103/physreva.33.1134 |
| [22] |
Ng W W, Panu U S, Lennox W C. Chaos based Analytical techniques for daily extreme hydrological observations[J]. Journal of Hydrology, 2007, 342(1/2): 17-41. Doi:10.1016/j.jhydrol.2007.04.023 |
| [23] |
Takens F. Detecting strange attractors in turbulence[M]//Lecture Notes in Mathematics. Berlin, Heidelberg: Springer Berlin Heidelberg, 1981: 366-381.
|
| [24] |
Abarbanel H D I, Brown R, Kadtke J B. Prediction and system identification in chaotic nonlinear systems: time series with broadband spectra[J]. Physics Letters A, 1989, 138(8): 401-408. Doi:10.1016/0375-9601(89)90839-6 |
 2023, Vol. 40
2023, Vol. 40 


