全球导航卫星系统(global navigation satellite system, GNSS)可为用户提供全方位、高精度的导航及授时信息。随着GNSS在智能设备及传感器网络中的普及，人们对GNSS接收机的性能及功耗要求更高。捕获模块作为GNSS信号接收中的关键步骤，运算量大、资源消耗多，是影响接收机接收性能的重要因素。

GNSS一般采用扩频调制技术，卫星信号的捕获需要进行多个码相位及大动态多普勒频率的搜索，搜索量较大。传统串行搜索方法，对信号所有可能的码相位和频率进行二维搜索，运算量大。因此，降低捕获模块运算量是接收机性能优化的关键。文献[1]提出一种基于圆周移位的并行码相位算法，将搜索中的多次快速傅里叶变换(fast Fourier transform，FFT)用计算量很小的频谱搬移来代替，使运算量大幅下降。文献[2]在基于FFT的并行码相位捕获算法基础上，提出稀疏傅里叶变换的方法，通过提高捕获过程中相关运算的效率，减少了运算量。文献[3]提出一种双块零扩展截断相关的捕获算法，根据复序列频谱的非对称性对信号进行截断预处理，同时结合双块零扩展与圆周移位，减少了运算量。

压缩感知(compressed sensing，CS)是由Donoho^[4]、Candes等^[5]提出的一种新的信号处理方法。该方法充分利用信号的稀疏特性，可大大降低信号的采样速率，为降低捕获所需的运算量提供了新途径。压缩感知用于GNSS信号捕获的关键点主要在于：信号稀疏性和合适的测量重构算法。基于这2个关键点，文献[6]提出以C/A码的正交基矩阵为稀疏域，利用卡尔曼滤波重构信号的压缩感知捕获算法，但重构过程复杂。文献[7]提出基于峰值位置的压缩感知方案，但稀疏矩阵存储量巨大。文献[8]将CS理论融入交错方向乘子法的框架, 提出一种高效的并行捕获算法。文献[9]提出基于压缩感知改进的部分匹配滤波FFT算法，降低了运算量和资源消耗，但没有考虑低信噪比问题。

本文基于对GNSS信号稀疏性的分析，利用C/A码构造稀疏矩阵，提出一种基于奇异值分解的压缩感知捕获方法，该方法通过对高斯随机测量矩阵进行奇异值平均，使其列向量线性非相干性更好，能更好地测量信号，改进后的测量矩阵测量所得的信号可保留更多信息，使得压缩感知捕获算法在较低信噪比条件下的捕获性能得到提高。

1 GNSS信号稀疏性

压缩感知过程有3个关键步骤：信号的稀疏表示、信号测量以及信号重构。其中信号的稀疏性是压缩感知应用的前提。

当长度为N的信号中只有K(K≪N)个非零的值，或其他值都接近于零时，我们认为信号具有稀疏性，其稀疏度为K。但通常实际处理信号不稀疏，这就需要对原始信号进行稀疏表示，即对原始信号进行某种变换，变换到某个域，使其在该域的表示是稀疏的。

以全球定位系统(global positioning system，GPS)为例，GNSS信号由载波、测距码和导航信息组成。在卫星发射端，先将测距码与导航信息调制为组合码，再通过载波扩频调制形成最终信号。接收信号时，射频前端接收信号并采样成为离散的中频信号，然后进行捕获处理，中频信号的数学表达式为

$ \begin{gathered} x(n)=A D(n) C(n) \exp \left(\mathrm{j}\left(\left(w_{\mathrm{IF}}+w_{\mathrm{d}}\right) n+\varphi\right)\right)+ \\ v(n), n=0, 1, \cdots, N-1 . \end{gathered} $

(1)

式中：A为信号幅度；D(n)为导航信息；C(n)为伪随机的测距码，即C/A码；w_IF为中频频率；φ为载波相位；w_d表示卫星与用户终端相对运动产生的多普勒频移；v(n)为高斯白噪声；N为信号长度。

C/A码是码率为1.023 Mbit/s的Gold码，码长为1 023。每个GPS卫星有唯一的C/A码，不同GPS卫星的C/A码相互正交，同一GPS卫星的C/A码及其循环移位序列也相互正交。卫星接收信号本身并不具有稀疏性，但由于C/A码良好的自相关性和互相关性，在码相位搜索域上，只有本地伪码相位与接收信号码相位对齐时相关结果才具有峰值，因此其码相关结果具有稀疏性, 可选择C/A码的循环移位矩阵作为信号的稀疏变换域^[6]。

假设$c(0)=\left[c_0, c_1, \cdots, c_{N-1}\right] \in \mathbb{R}^{N \times 1} $为任意GPS卫星的C/A码，将其循环移位i个码片后，得到序列$c(i)=\left[c_i, c_{i+1}, \cdots c_{N-1}, c_0, \cdots c_{i-1}\right] \in \mathbb{R}^{N \times 1} $，i=0, 1, …N-1。构造稀疏矩阵如下：

$ \boldsymbol{G}=\left(\begin{array}{cccc} c_0 & c_1 & \cdots & c_{N-1} \\ c_1 & c_2 & \cdots & c_0 \\ \vdots & \vdots & & \vdots \\ c_{N-1} & c_0 & \cdots & c_{N-2} \end{array}\right) . $

(2)

捕获是通过2次相关进行多普勒频率和C/A码相位的二维搜索，根据相关峰位置获得频率和码相位估计值。首先载波发生器产生本地载波$\exp \left(-\mathrm{j}\left(\left(w_{\mathrm{IF}}+\hat{w}_{\mathrm{d}}\right) n+\hat{\varphi}\right)\right), \hat{w}_{\mathrm{d}} $为多普勒频率估计值，$ \hat{\varphi}$为本地载波相位。产生的本地载波与输入的中频信号相关，剥离载波及多普勒，下变频信号为

$ \begin{gathered} r\left(n, \hat{w}_{\mathrm{d}}\right)=x(n) \exp \left(-\mathrm{j}\left(\left(w_{\mathrm{IF}}+\hat{w}_{\mathrm{d}}\right) n+\hat{\varphi}\right)\right)= \\ A D(n) C\left(n, \hat{w}_{\mathrm{d}}\right) \exp \left(\mathrm{j}\left(\left(w_{\mathrm{d}}-\hat{w}_{\mathrm{d}}\right) n+\varphi-\hat{\varphi}\right)\right)+ \\ v_r(n), n=0, 1, \cdots, N-1 . \end{gathered} $

(3)

根据式(2)可对$r\left(n, \hat{w}_d\right) $进行稀疏表示如下

$ r\left(n, \hat{w}_{\mathrm{d}}\right)=\boldsymbol{G}\left[\begin{array}{c} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_{N-1} \end{array}\right]+v_r(n)=\boldsymbol{G} \boldsymbol{\theta}+v_r(n), $

(4)

式中：θ=β[p(0), p(1)，…，p(N-1)]^T是$ r\left(n, \hat{w}_{\mathrm{d}}\right)$在码域的系数表示向量, [p(0), p(1)，…，p(N-1)]^T为C/A码的相位信息，β=$ A D(n) \exp \left(\mathrm{j}\left(\left(w_{\mathrm{d}}-\hat{w}_{\mathrm{d}}\right) n+\varphi-\hat{\varphi}\right)\right)$为信号幅度相位及导航数据的表示。v_r(n)为下变频信号的噪声分量，在信号稀疏性分析中可不做考虑。可将下变频信号简化表示为r=Gθ.如果多普勒频率搜索成功，即$ \hat{w}_{\mathrm{d}}=w_{\mathrm{d}}$，则θ是一个稀疏向量，仅有少数较大的非零值，其峰值位置为C/A码相位估计值。如果多普勒的估计值误差较大，其稀疏性就会受到影响，峰值位置不明显。基于式(4)中GPS信号的稀疏表示，可利用压缩感知理论完成对码相位的搜索。

2 改进的压缩感知捕获算法 2.1 基于奇异值分解的测量矩阵构造

信号的测量是进行信号由高维到低维的映射，使用和稀疏矩阵G不相关的M×N(M≪N)维的测量矩阵B对信号进行压缩采样，定义压缩比a=M/N。得到M×N维的测量序列：即

$ \boldsymbol{Y}=\boldsymbol{B r}. $

(5)

测量矩阵B必须保证不会把2个不同的稀疏信号映射到同一个采样集中，这就要求测量矩阵中任意M个列向量组成的矩阵行列式不为零，即为非奇异矩阵^[10]。

满足上述条件的矩阵可作为测量矩阵对矩阵进行压缩。目前测量矩阵主要有随机矩阵、确定性矩阵和部分随机矩阵等^[11]。高斯随机测量矩阵与大多数正交稀疏矩阵都不相关，是压缩感知中适应性最广的测量矩阵^[10]，但其自身的不确定性会造成捕获结果的不确定性，使捕获成功率下降。本文根据奇异值分解(singular value decomposition，SVD)^[12]对其进行改进。

奇异值分解定理如下：设S是秩为z(0 < z)的m×n阶实矩阵，则存在一个分解使得

$ \boldsymbol{S}=\boldsymbol{U}\left(\begin{array}{ll} \boldsymbol{\varSigma} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{0} \end{array}\right) \boldsymbol{V}^{\mathrm{T}}, $

(6)

其中：$ \boldsymbol{\varSigma}=\left(\begin{array}{ccc} \sigma_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_z \end{array}\right)$，U是m×m阶酉矩阵；V^T即V的共轭转置，是n×n阶酉矩阵，这样的分解就称作矩阵S的奇异值分解，σ₁, σ₂, …，σ_z为S的全部奇异值，且σ₁≥σ₂≥σ₃≥…σ_z > 0。

设‖S‖_p是与向量范数‖X‖_p相容的范数，则有当奇异矩阵S，存在S⁺，若向量X₁，X₂分别满足SX₁=Y₁，SX₂=Y₂，令$ d_1=\frac{\left\|\boldsymbol{X}_1-\boldsymbol{X}_2\right\|_p}{\left\|\boldsymbol{X}_1\right\|_p}, d_2=\frac{\left\|\boldsymbol{Y}_1-\boldsymbol{Y}_2\right\|_p}{\left\|\boldsymbol{Y}_1\right\|_p}$, 则有

$ \frac{d_1}{d_2} \leqslant\|\boldsymbol{S}\|_p \cdot\left\|\boldsymbol{S}^{+}\right\|_p . $

(7)

根据矩阵奇异值理论可知：矩阵奇异值代表矩阵中隐含的特征信息^[13]，且特征重要性和奇异值大小成正比。

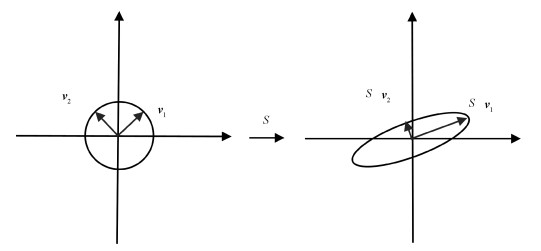
几何上来说SVD就是将一个复杂的空间变换分解为3个基本变换，V是旋转，Σ是缩放，U是投影。以二维矩阵的图解为例，在图 1中：奇异值σ_i就是映射后的正交基u_i的模的大小，即σ_i=|Sv_i|，向量u_i为Sv_i方向上的单位向量。

结合矩阵理论，奇异值σ_i衡量每个列向量对于S的权重，表示矩阵S对应的第i个列向量在子空间的分布。矩阵S的z个奇异值的大小差距越小，则表明其列向量分布越分散，其线性独立性越好，符合压缩感知对于测量矩阵的要求。

本文基于以上分析，对高斯随机测量矩阵进行改进：先得到高斯随机测量矩阵B，B是一个M×N(M≪N)的矩阵；然后对其进行奇异值分解，得到奇异值；最后通过求奇异值均值得到改进的测量矩阵B，使矩阵的列向量分布更随机，从而含有更多信息，使测量后的信号更完整，便于之后更好的重构。算法如下:

1) 生成高斯随机测量矩阵B_M×N

$ \begin{gathered} \boldsymbol{B}_{i, j} \sim N\left(0, \frac{1}{M}\right) \\ i=1, 2, \cdots, M ; j=1, 2, \cdots, N . \end{gathered} $

(8)

2) 对B进行奇异值分解

$ \boldsymbol{B}=\boldsymbol{U}\left(\begin{array}{ll} \boldsymbol{\varSigma} & \mathit{\pmb{0}} \\ \mathit{\pmb{0}} & \mathit{\pmb{0}} \end{array}\right) \boldsymbol{V}^{\mathrm{T}}. $

(9)

其中：$\boldsymbol{\varSigma}=\left(\begin{array}{ccc} \sigma_1 & \cdots & 0 \\ \vdots & & \vdots \\ 0 & \cdots & \sigma_M \end{array}\right), \sigma_1 \geqslant \sigma_2 \geqslant \cdots \sigma_M $.

3) 对Σ对角线上的值求平均Mean=(σ₁+σ₂+…σ_M)/M；令

$ \overline{\boldsymbol{\varSigma}}=\left(\begin{array}{ccc} \sigma_1^{\prime} & \cdots & 0 \\ \vdots & & \vdots \\ 0 & \cdots & \sigma_M^{\prime} \end{array}\right). $

(10)

其中：$\sigma_1^{\prime}=\sigma_2^{\prime}=\cdots \sigma_M^{\prime}=\text { Mean } $。

4) 得到改进的测量矩阵

$ \overline{\boldsymbol{B}}=\boldsymbol{U}\left(\begin{array}{ll} \overline{\boldsymbol{\varSigma}} & \mathit{\pmb{0}} \\ \mathit{\pmb{0}} & \mathit{\pmb{0}} \end{array}\right) \boldsymbol{V}^{\mathrm{T}}. $

(11)

根据矩阵奇异值的分析可知：以上改进保证矩阵的空间几何度量不变的同时，避免了所选列特征冗余。改进的测量矩阵B最小奇异值得到增大，线性非相干性较好，能更好地测量信号，且在相同范数意义下有更高的重构精度^[14]。

得到新的测量矩阵之后，就可以利用式(5)对信号进行测量，得到测量信号Y。

$ \boldsymbol{Y}=\boldsymbol{B r}=\boldsymbol{B G \theta}. $

(12)

其中，BG定义为感知矩阵A_(M×N)

$ \boldsymbol{A}_{(M \times N)}=\boldsymbol{B} \boldsymbol{G}. $

(13)

感知矩阵是信号重构的关键，基于文献[15]感知矩阵互不相关性理论: 对于相互不相关性较小的感知矩阵，能够很好地满足RIP。互不相关性定义：$ \mu(\boldsymbol{A})=\max \limits_{i \neq j} \frac{\left|\boldsymbol{A}_i^{\mathrm{T}} \boldsymbol{A}_j\right|}{\boldsymbol{A}_i^{\mathrm{T}} \boldsymbol{A}_i}$，A_j为列向量。互不相关性越小，感知矩阵越能准确地恢复稀疏信号。通过对不同压缩比下的高斯随机矩阵及奇异值改进的矩阵的μ值计算对比，改进矩阵μ值均略小，表明改进矩阵的互不相关性更小，理论上能更好恢复信号。捕获结果也表明改进的感知矩阵能使信号捕获成功率得到提升。

2.2 信号重构

信号的重构是由测量信号Y及感知矩阵A求解稀疏信号θ的过程，这是一个求解欠定方程组的问题，在信号稀疏或可压缩的前提下，求解欠定方程组的问题可转化为最小l₀范数问题。最小l₀范数在一定条件下和最小l₁范数具有等价性, 可得到相同的解，则该问题可以转化为最小l₁范数下的最优化问题^[5]

$ \min \|\boldsymbol{\theta}\|_1 \text { s. t. } \boldsymbol{A} \boldsymbol{\theta}=\boldsymbol{Y} . $

(14)

这样的转化使得问题变成了一个凸优化问题, 于是可以方便地化简为线性规划问题。常用的重构算法有贪婪算法、凸优化、迭代阈值等^[16]。

利用测量信号Y及感知矩阵A_(M×N)对信号进行重构，基于信号捕获的特殊性，重构算法只需重构稀疏度很小的稀疏信号，且主要关注峰值位置，可选择计算量小、稳定的正交匹配追踪(orthogonal matching pursuit, OMP)算法^[6]。

重构得到稀疏估计数据$\hat{\boldsymbol{\theta}} $后，该频率点的搜索即结束。改变多普勒频率，进行下一个频率点的搜索。将所有频率范围搜索完毕后，找出相关值最高峰，该最高峰值与该频率下的平均相关值的比值大于门限V_t时，则捕获成功，记录该恢复信号对应的多普勒频移和码相位；否则捕获失败。

2.3 算法框图

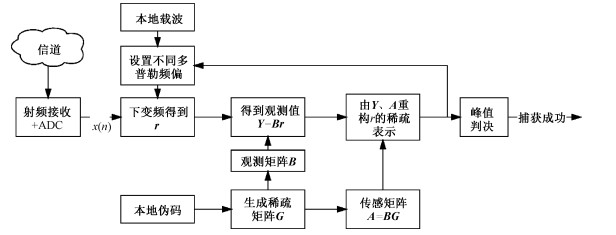
基于以上分析，本文提出基于奇异值分解的压缩感知(SVD-CS)捕获算法，其算法流程如图 2所示：对于接收机射频接收并ADC采样的中频数字信号x(n)进行捕获处理，首先初始化捕获参数，基于本地伪码的循环相关获得稀疏矩阵G，根据式(8)~式(11)获得随机测量矩阵B，并由式(13)计算出传感矩阵A；然后在本地载波基础上设置多普勒估计值，根据式(3)剥离中频信号x(n)的载波和多普勒频率，得到信号$r\left(n, \hat{w}_{\mathrm{d}}\right) $；接着利用本文改进测量矩阵测量并重构信号得到$ \hat{\boldsymbol{\theta}}$，结束该频点搜索；最后遍历所有多普勒估计值，找出峰值，门限判别捕获是否成功。捕获成功后输出到下一步进行处理。

3 仿真与分析 3.1 计算复杂度分析

捕获算法的计算复杂度主要是因为需要多次相关运算。本文算法的测量过程可视为由测量矩阵与输入信号进行相关运算，测量矩阵的M个行向量可视为M个压缩相关器，完成对输入信号的相关运算。因此在引入压缩感知理论对传统串行捕获算法进行改进之后，在相关器数量上降低到1/a，同时数据量的降低也减少了寄存器等资源消耗和后续信号处理压力。

捕获中一周期信号的相关次数取决于码相位搜索精度、频率搜索步长及多普勒频率搜索范围3个值的大小。本文算法主要对信号码域进行压缩，频率点的搜索与传统串行算法的搜索次数一致，所以简化频域搜索分析，主要以长度为N的信号为例进行每个频点的计算复杂度分析。

对于传统串行的捕获算法，在每个频率点需要对码相位偏移N次，每次偏移进行一次N点相关计算并累加，一共需要N×N次乘法，N×(N-1)次加法，其算法复杂度为O(N²)。

对于本文算法，计算量主要由相关运算及信号重构产生。当测量矩阵为M×N的矩阵时，本文相关运算需要M×N次乘法，M×(N-1)次加法，计算复杂度为O(MN)。OMP重构算法的复杂度目前已有很多文献进行分析^[17-18]，其计算量约为O(KMN)；最后关于测量矩阵改进部分的计算量主要体现在奇异值分解，可提前计算存储，对捕获过程计算量不产生影响。所以压缩感知算法的复杂度为O(KMN)。表 1为各算法计算量对比。

3.2 仿真

对本文提出的基于奇异值分解的压缩感知捕获算法(SVD-CS)进行仿真。模拟产生通过加性高斯白噪声信道的接收信号，中频频率40 MHz，捕获时假设信号降采样到2.046 MHz，每次取2 046个点进行相关运算，随机产生码相位偏移及频率偏移。捕获中码相位搜索步长设为半码片。频率搜索步长设为500 Hz，门限值V_t设为2。

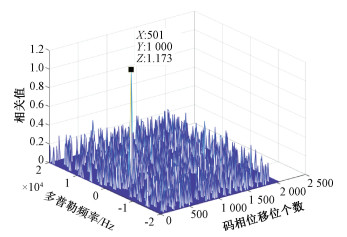
图 3是信噪比为-15 dB，测量长度为512，重构稀疏度设为10时本文算法的捕获结果。捕获结果出现明显的峰值，表明捕获到了信号。同时，峰值位置对应的多普勒频率与码相位结果与模拟接收信号的结果一致。结果表明，本文算法能成功捕获信号。

图 4是同信噪比下，捕获性能的分析与对比，以传统高斯矩阵捕获算法(GS-CS)^[19]作为对照组，信噪比为-15 dB。(a)是测量长度M与捕获成功率曲线图，(b)是稀疏度K与捕获成功率曲线图，由仿真结果可知：在同信噪比下，SVD-CS算法在不同测量长度，不同稀疏度下捕获结果均明显优于GS-CS算法，且测量长度越大捕获结果越好，稀疏度越小捕获结果越好。

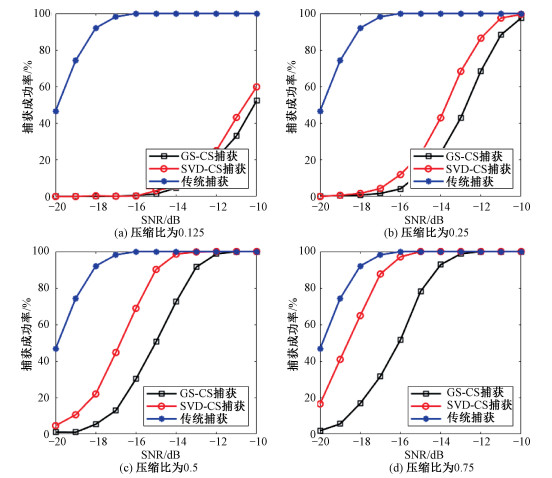
图 5是不同信噪比下，以传统串行算法为对照组，GS-CS算法与本文SVD-CS算法的捕获性能对比，本组仿真中稀疏度设为1。通过4组不同测量长度对比可知：在一定信噪比范围内，不同测量长度本文算法的捕获成功概率均有明显提高，且压缩比越大，提高越明显，表明本文算法改进的有效性。

表 2是不同信噪比下本文算法的最小测量长度M_min仿真。M_min定义为捕获成功率能达到90%的最小测量长度。仿真表明该算法在一定信噪比下可以以较小的测量长度达到捕获性能要求，且信号信噪比越高，算法减少运算量的优势越明显。

4 总结

基于GNSS信号的稀疏性，压缩感知可用于信号捕获，降低捕获过程的运算量，但其算法在低信噪比条件下的捕获概率会有较大的降低。本文以提高捕获概率为目标，从改进测量矩阵出发，提出一种基于奇异值分解的压缩感知捕获算法。首先基于GNSS信号稀疏性构造稀疏矩阵；其次，对高斯随机测量矩阵进行奇异值平均，产生新的测量矩阵，最后利用稀疏矩阵和新的测量矩阵完成信号的压缩感知捕获。仿真结果验证了本文算法的有效性，在计算量略有增加的情况下，可明显提高一定信噪比条件下压缩感知捕获算法的捕获性能。