2. 中国科学院大学材料科学与光电技术学院材料科学与光电工程中心, 北京 100049;
3. 中国科学院过程工程研究所绿色过程与工程重点实验室, 北京 100190;
4. 东方汽轮机有限公司长寿命高温材料国家重点实验室, 四川 德阳 618000
2. Center of Materials Science and Optoelectronics Engineering, College of Materials Science and Opto-Electronic Technology, University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Green Process and Engineering, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China;
4. State Key Laboratory of Long-Life High Temperature Materials, Dongfang Turbine Co., Ltd, Deyang 618000, Sichuan, China
电磁冶金技术经过近100年的发展,在电磁感应加热、电磁搅拌、电磁制动、电磁净化等领域取得长足进步[1-4],已经成为生产高质量金属材料必不可少的技术之一。电磁搅拌技术具有非接触、易控制以及环保等优点,能有效控制高电导率金属熔体(> 105 S/m)的三传过程[5-8]。目前电磁搅拌技术在低电导率液体(小于102 S/m)上的应用十分少见,技术手段尚不成熟且暂无成型产品。然而,低电导率液体的驱动和强化传输的应用场合却十分广泛,常见的化学化工领域的大多数液体,冶金中的高温熔融氧化物等都属于低电导率液体的范畴[9]。就搅拌流体的特点而言,机械搅拌方式其速度场主要集中在搅拌桨叶附近[10],速度场梯度大,流场分布不均匀,而电磁驱动的方式由于洛伦兹力是体积力,在优化的磁场设计下,洛伦兹力可均匀地作用在整个导电液体上,使得搅拌更加均匀和充分[11]。并且,电磁驱动是一种非接触式的驱动方式,能在高温、高压以及强腐蚀性等不适合机械搅拌的环境中使用。
传统的电磁搅拌技术不适合低熔点液体驱动的原因在于,工业中常用的电磁搅拌的工作频率一般小于10 Hz[12-13],由于低电导率液的电导率相较于金属液低了几个数量级,所产生的洛仑兹力相当弱,无法实现电磁搅拌的目的。Ernst等[14]根据单相异步电机的原理,设计了工作频率100 kHz以上的高频电磁搅拌器,实现了电导率为40 S/m的NaCl溶液的cm/s量级的电磁驱动。这意味着将电磁搅拌技术应用范围从高电导率金属液(105~107 S/m量级)拓展到低电导率液体(1~102 S/m量级),无疑是个巨大的技术进步。李勇[15]进行了高频行波磁场的理论分析,并从电路分析角度,通过探究两相线圈距离对互感系数的影响,寻找到最佳的电路工作点,从而实现对低电导率液体的有效搅拌,但其并未研究不同电学参数对低电导率液体传输的影响。由于实际电学参数相互影响且高频磁场的热效应显著,为非线性动力学问题,实验规律复杂,本文在Ernst等[14]和李勇[15]模拟与实验工作的基础上,采用多物理场耦合的数值模型,以流场速度大小的平均值为评判标准,探究各参数对低电导率液体驱动效果的影响,可为高频行波磁场的电路优化提供参考。
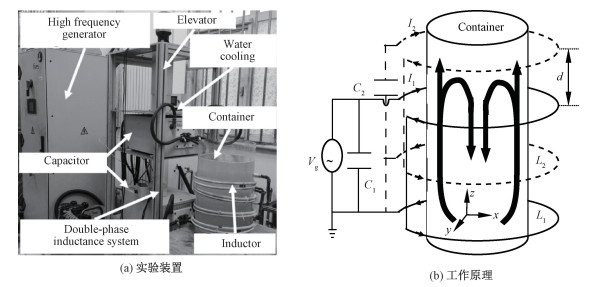
1 高频行波磁场装置描述 1.1 高频行波磁场的工作原理高频行波磁场装置实物如图 1(a)所示,该装置的设计受单相异步电动机的原理启发,主要由高频电源、电容组以及两相电感系统组成。图 1(b)的示意图中,驱动相线圈L1(实线线圈)与高频电源V1相连接并与电容C1并联构成驱动相回路,感应相线圈L2(虚线线圈)与电容C2并联构成感应相回路。其中,驱动相线圈和感应相线圈均由上下2个反向绕制连接起来的线圈组成,该绕制方式使得同一相线圈的上下2个线圈中的电流方向相反。当高频电源通电时,驱动相线圈中间产生高频电流I1,从而在驱动相线圈周围产生高频磁场,该磁场与感应相线圈相互感应,使得感应相线圈中也产生高频电流I2。通过计算并配置合适的电容值,并通过实验调整两相线圈的间距d获得合适的两相间的互感,使得I1与I2产生一定的相位差,从而在容器的轴线方向上形成高频行波磁场,其中行波磁场的运动方向取决于相位差,当I2滞后于I1时,磁场运动方向向上,反之磁场运动则向下。低电导率液体在高频行波磁场中感应出涡流,若行波磁场的运动方向向上,涡流与行波磁场相互作用后,低电导率液体将受到持续向上的洛伦兹力,从而达到如图 1(b)中所示的驱动低电导率液体的目的。
|
Download:
|
| 图 1 高频行波磁场的实验装置和工作原理图 Fig. 1 Experimental device and working principle diagram of high frequency traveling wave magnetic field | |
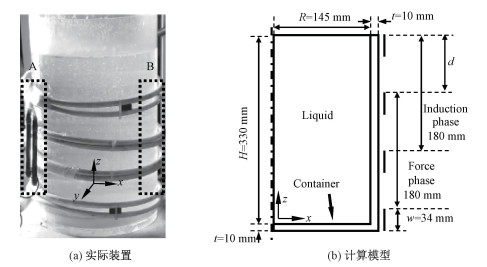
主要研究两相线圈中电流的大小、相位差和频率以及两相线圈间距对容器内低电导率液体传输的影响,且不考虑高频电源的感性变化,只对容器内低电导率液体与两相线圈部分建模,如图 2(a)所示。虽然图 2(a)中区域A与区域B处的线圈由于绕制原因并不完全对称,但根据几何特征与物理场特征,为简化模型并减少计算量,采用二维轴对称模型,如图 2(b)所示。其中驱动相线圈和感应相线圈的上下2个反绕串联线圈的距离均为固定值180 mm,两相线圈之间的距离d可调节,变化范围为40~120 mm,线圈中的电流大小I变化范围为100~900 A,两相线圈电流相位差φ变化范围为0°~180°,线圈电流频率f变化范围为100~400 kHz。
|
Download:
|
| 图 2 高频行波磁场的计算模型 Fig. 2 A computational model of high frequency traveling wave magnetic field | |
该问题为磁流耦合的多物理场问题,为便于数学建模作如下假设与简化:1)位移电流忽略不计;2)被驱动的低电导率液体的特征速度为10-2 m/s量级,磁雷诺数Rm很小,约为10-6,因而可忽略液体流动对电磁场的影响;3)低电导率液体为弱可压缩流体,其密度随温度变化,变化关系为ρ=12 010.1-80.4T+0.31T2-5.38×10-4T3+3.63×10-7T4,其中ρ为密度(kg/m3),T为温度(K)。4)假设低电导率液体的电导率、黏度、等压热容以及热导率均不随温度变化,具体数值如表 1所示。
|
|
表 1 低电导率液体属性 Table 1 Properties of the low conductivity liquid |
电磁场控制方程:
为求解容器内的电磁场分布,需求解简化的Maxwell方程组:
| $ \begin{aligned} & \nabla \times \boldsymbol{E}=-\frac{\partial \boldsymbol{B}}{\partial t}, \nabla \times \boldsymbol{H}=\boldsymbol{J}, \nabla \cdot \boldsymbol{B}=0, \\ & \boldsymbol{B}=\mu_{\mathrm{m}} \boldsymbol{H}, \boldsymbol{J}=\sigma \boldsymbol{E}, \end{aligned} $ | (1) |
其中:E为电场强度,V/m;B为磁感应强度,T;t为时间,s;H为磁场强度,A/m;J为电流密度,A/m2;μm为磁导率,H/m;σ为电导率,S/m。
电磁场与流场耦合计算时采用时均电磁体积力:
| $ \boldsymbol{F}_{\mathrm{m}}=\frac{1}{2} \operatorname{Re}\left(\boldsymbol{J} \times \boldsymbol{B}^*\right), $ | (2) |
其中:Fm为时均电磁力,N/m3;B*为B的共轭复数;Re为取复数的实部。
连续方程:
| $ \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho \boldsymbol{u})=0, $ | (3) |
式中:ρ为流体密度,kg/m3;u为流体速度,m/s。
动量方程:
不考虑热对流的情形:
| $ \rho \frac{\mathrm{d} \boldsymbol{u}}{\mathrm{d} t}=-\nabla p+\mu \nabla^2 \boldsymbol{u}+\rho \boldsymbol{g}+\boldsymbol{F}_{\mathrm{m}}, $ | (4) |
式中: t为时间,s;p为压强,N/m2;μ为动力黏度,Pa·s;g为重力加速度,m/s2。
考虑热对流的情形,采用Boussinesq近似:
| $ \rho \frac{\mathrm{d} \boldsymbol{u}}{\mathrm{d} t}=-\nabla p+\mu \nabla^2 \boldsymbol{u}+\beta_0\left(T-T_0\right) \boldsymbol{g}+\boldsymbol{F}_{\mathrm{m}}, $ | (5) |
式中:β0为参考点的热膨胀系数,1/K;T为热力学温度,K;T0为参考点的温度,K。
能量方程:
| $ \rho c_{\mathrm{p}} \frac{\mathrm{d} T}{\mathrm{~d} t}=\nabla \cdot(\lambda \nabla T)+Q, $ | (6) |
式中:λ为流体的热导率,W/(m·K);cp为流体的等压热容,J/(kg·K);Q为焦耳热,W/m3。
| $ Q=\frac{J^2}{\sigma}, $ | (7) |
该模型使用多物理场软件COMSOL 5.5进行数值模拟计算,电磁场边界条件为磁力绝缘。计算流场时容器壁面为无滑移边界条件,流体液面为开放边界条件。计算温度场时,容器壁面设为绝热边界条件,液面设为对流传热边界条件,对流传热系数设为10 W/(m2·K)。
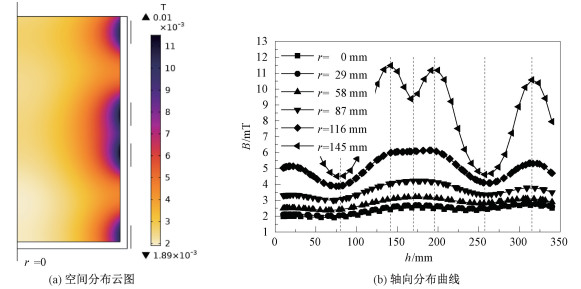
2 结果与讨论 2.1 磁场分布特征的数值模拟结果图 3为磁感应强度的模(B)在容器中的分布,其中I为900 A,f为400 kHz,φ为90°,d为120 mm。如图 3(a)所示,B的空间分布与两相感应线圈的位置有关,距离线圈越近的位置B越大,最大值为11.48 mT,最小值为1.89 mT,这与工业上的工频或低频电磁搅拌技术中磁场的量级相仿。图 3(b)表明在相同高度下离中心轴线越远B越大,且在线圈对应高度位置的B为极大值,相邻线圈的中心高度位置的B为极小值。
|
Download:
|
| 图 3 磁感应强度模的分布 Fig. 3 Distribution of the modulus of magnetic induction intensity | |
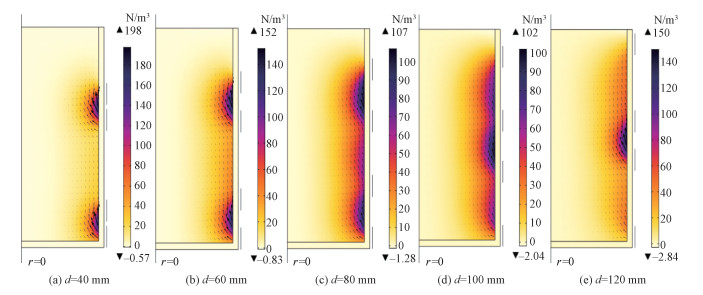
图 4为不同d对应的电磁力(Fm)分布,其中I为900 A,f为400 kHz,φ为90°。由图 4(a)~4(e)可以得出Fm的分布形式与线圈的位置有关,Fm主要集中在两相线圈之间,且线圈的距离越近,线圈间的Fm越大。在d=40 mm处最大的电磁力为198 N/m3,在d=100 mm时,最大的电磁力为107 N/m3。造成这一现象的原因主要有2个,其一是磁感应强度分布在线圈附近最强,其二是磁场主要在两相线圈之间运动,导致感应电流密度在两相线圈之间最大。根据式(2)可得在线圈之间的电磁力较其他区域更大。
|
Download:
|
| 图 4 不同d对应的电磁力分布 Fig. 4 Distribution of electromagnetic force at different d values | |
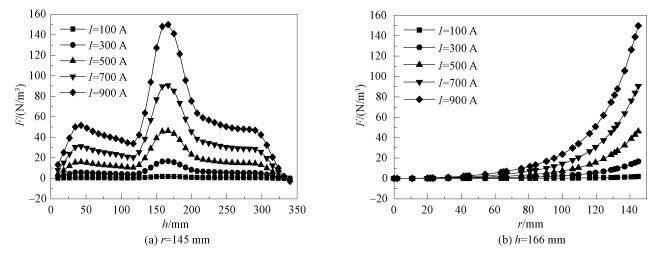
图 5为不同线圈电流强度(I)时的轴向电磁力大小(F)分布,其中f为400 kHz,φ为90°,d为120 mm。由图 5(a)可见,容器边缘的F在166 mm高度处最大,这与图 4(e)所示的电磁力分布一致。F的最大值由I=100 A时的1.85 N/m3增加到I=900 A时的149.84 N/m3。经曲线拟合后可得F的最大值与I的平方成正比,这与Maxwell方程组推导结果是一致的,可见I对F的影响很大。图 5(b)为容器高度166 mm处F的径向分布,F由中心向容器边界逐渐增大,且F与径向位置r近似成指数函数关系。因此容器中的电磁力主要集中在容器的壁面附近,类比于趋肤深度的计算,在r≥122 mm时
|
Download:
|
| 图 5 不同电流强度时的轴向电磁力分布 Fig. 5 Axial electromagnetic force distribution of different current intensities | |
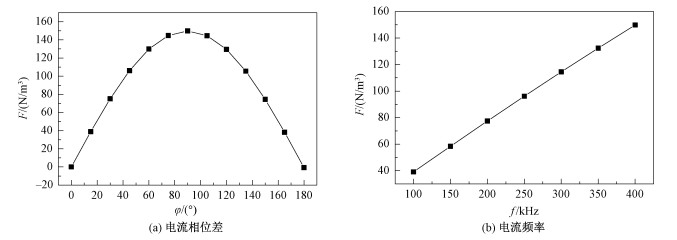
图 6(a)为不同相位差的轴向电磁力大小,其中I为900 A,f为400 kHz,d为120 mm,r为145 mm,h为166 mm。由图 6(a)可知,F随φ增大先增大而后减小,在ϕ=90°达到最大值。这是因为在单相异步电机的原理中,只有在相位差为90°时才能在线圈内产生持续运动的行波磁场,类似地,此时流体中的感应电流最大,根据公式(2)可知此时的电磁力最大。在大于或者小于90°时磁场不能形成稳定的定向运动,因而电磁力较小。线圈电流的相位差在75°~105°的范围内时电磁驱动力可达到最大电磁驱动力的96.6%以上,因此,选取这个相位差区间可获得较大的电磁力。
|
Download:
|
| 图 6 轴向电磁力大小随线圈电流相位差和电流频率的变化 Fig. 6 Variation of axial electromagnetic force magnitude with coil current phase difference and current frequency | |
图 6(b)是轴向电磁力大小随线圈电流频率变化的关系图,其中I为900 A,d为120 mm,φ为90°,r为145 mm,h为166 mm。由图 6(b)可知轴向电磁力与线圈电流频率成线性关系, 频率越大,轴向电磁力越大。当频率f从100 kHz增加到400 kHz时,电磁趋肤深度δ=1/
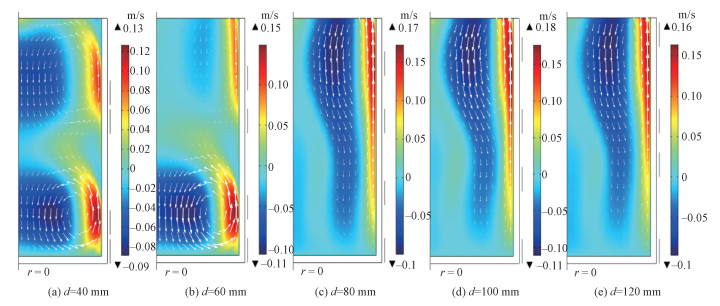
由于实验过程中电磁力驱动和热对流的效应无法分开,并不能考察电磁力驱动效果在其中所占的比例,本文采用对比模拟的策略:首先仅考虑电磁力的驱动,再研究同时考虑电磁力与热对流时的驱动效果。图 7为不考虑热对流时,计算时间在300 s,流场稳定时不同线圈距离的流场分布,其中I为900 A,f为400 kHz,φ为90°。图 7中红色表示轴向速度分量为向上,蓝色表示轴向速度分量向下,白色箭头为流速的方向。从图中可以看出流场分布的形式与线圈之间的距离有关,在线圈距离较小时,如d=40 mm时,流场分布为两涡结构,2个涡旋的旋转方向均为逆时针方向,且向上最大流速为0.13 m/s,向下最大流速为0.09 m/s。随着线圈距离的增大,流场的分布形式逐渐从双涡漩转化为单个大环流,旋转方向依旧为逆时针,在d=80 mm时流场形式转变为单个大环流,且最大向上流速为0.17 m/s,最大向下流速为0.1 m/s。图 4中随着d增大电磁力从2个集中区转变为一个集中区,因此电磁力的分布形式的转变可以解释这种流场形式的转变。
|
Download:
|
| 图 7 不同d的子午面上的流场分布 Fig. 7 The distribution of the flow field on the meridian plane of different d values | |
为评价高频行波磁场的驱动效果,本文采用容器内流场流速大小的平均值v为评价标准,v的计算式如下:
| $ v=\frac{\iint\limits_{\mathrm{A}} V \mathrm{~d} S}{\iint\limits_{\mathrm{A}} \mathrm{d} S}, $ | (8) |
其中: v为容器内流场流速大小的平均值,m/s;A为计算域;V为流场流速大小,m/s;dS为面元,m2。
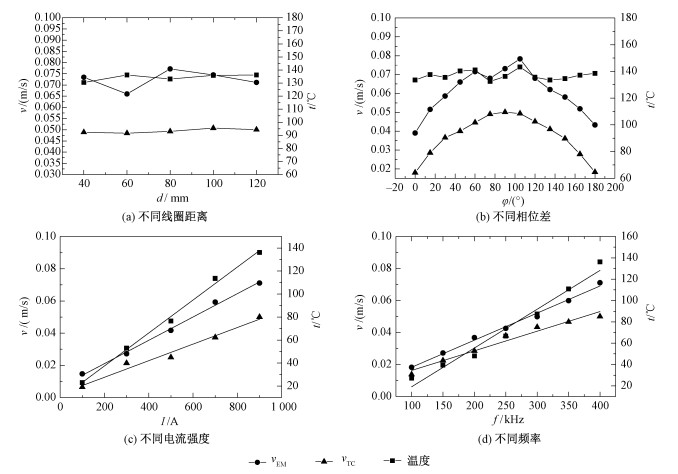
图 8为不同操作参数对容器内流场流速大小的平均值(vEM为仅电磁力驱动的平均流速,vTC为电磁力与热对流共同作用的平均流速)以及平均温度(t)的影响,其中I为900 A,f为400 kHz,φ为90°,d为120 mm。从图 8的4幅图可得出,在考虑热对流后的vTC整体上比仅考虑电磁力驱动时的vEM大。如图 8(a),尽管d不同会影响流场的流动形态,但不同的d对v以及t的影响并不大,其中vEM变化范围是0.048 6~0.507 m/s,vTC变化范围为0.066~0.077 m/s。这是因为从能量守恒的角度分析,仅改变d并不会改变线圈中的电能馈入到流体内的热能与动能。由此可知在设计高频行波磁场装置时,可以通过调整线圈的距离来获得合适的流场分布形式。图 8(b)表明t并不随电流相位差明显变化,而平均流速随电流相位差先增大后减小,在ϕ=90°附近达到最大值。电磁力对流体做功转化为流体的动能,而电磁力所做的功与电磁力成正比,因此图 8(b)与图 6(a)轴向电磁力大小和线圈电流相位差的关系类似。由式(1)~式(2)以及式(7)可推得流体获得的动能均与I2和f2成正比,因此图 8(c)与8(d)均显示了I与f对v成线性关系。当电流大于700 A或频率大于350 kHz,在通电300 s时流体的t大于100 ℃,因此在使用高频行波磁场驱动低电导率液体时应注意该液体的沸点,以及适宜的工作温度范围。
|
Download:
|
| 图 8 不同操作参数对平均流速以及平均温度的影响 Fig. 8 The influence of different operation parameters on average flow rate and average temperature | |
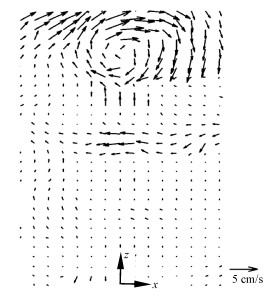
图 9是使用粒子图像测速软件分析得到的高频行波磁场驱动下的流场分布,其中实验条件是: f为237 kHz,φ为48°,d为120 mm,|I1/I2|为0.623。由于分析区域有线圈遮挡,遮挡区域的流速计算结果偏小。图 9中显示在容器的最上方形成了一个顺时针的流场,且最大流速可达4.8 cm/s,平均流速达1.1 cm/s,这证明高频行波磁场可以驱动低电导率液体。容器区域A的线圈由于绕制方式的原因数量多于区域B,如图 2(a)所示。这导致流体受到的电磁力不对称,因此流场不是轴对称分布。使用图 9相同操作参数进行数值计算可得流场中最大流速为7.2 cm/s,平均流速为2.8 cm/s。因此从驱动效果上分析,实验和数值模拟结果均证明了高频行波磁场驱动低电导率液体的有效性。
|
Download:
|
| 图 9 实验测量的流场分布 Fig. 9 The flow field distribution of experimental measurement | |
高频行波磁场对低电导率液体具有显著的驱动效果,这是一种较为新颖的低电导率液体的驱动方式,对流体的三传一反过程可能起到强烈地促进作用。本文针对该驱动方式建立了多物理场磁流耦合数值模型。通过该模型研究电流大小、频率、相位差以及线圈距离对容器内电磁场、流场以及温度场的影响,探究它们对驱动的具体影响,并获得最佳的工作参数。同时,还验证了高频行波磁场驱动低电导率液体的可行性。研究结论如下:
1) 在研究电磁力对流场分布的影响时,发现两相线圈距离对流场分布形式有明显的影响,随线圈距离增加子午面上的流场形态逐渐从2个涡流转变为单个大环流,因此可以通过设计线圈结构来满足不同的流场形态需求。
2) 电流相位差对平均流速的影响是先增大后减小,并在φ=90°附近达到最大值,因此在设计高频行波磁场发生装置时可通过调节相位差在这一范围内来获得较好的驱动效果。
3) 电流大小与频率对平均温度与平均流速的影响均为线性关系。在驱动时间达到300 s时,若频率较高或电流较大则液体温度会超过100 ℃,因此电流的大小和频率并不是越高越好,应在所选液体的适用温度范围内选取最大的电流与频率。
4) 数值和实验结果均表明被驱动流体具有cm/s量级的流动强度。
| [1] |
任忠鸣, 雷作胜, 李传军, 等. 电磁冶金技术研究新进展[J]. 金属学报, 2020, 56(4): 583-600. Doi:10.11900/0412.1961.2019.00373 |
| [2] |
Li X, Wang X H, Bao Y P, et al. Effect of electromagnetic stirring on the solidification behavior of high-magnetic-induction grain-oriented silicon steel continuous casting slab[J]. The Journal of the Minerals, Metals & Materials Society, 2020, 72(10): 3628-3633. Doi:10.1007/S11837-020-04058-y |
| [3] |
Liu H P, Wang X H, Si L Y, et al. Numerical simulation of 3D electromagnetic-thermal phenomena in an induction heated slab[J]. Journal of Iron and Steel Research International, 2020, 27(4): 420-432. Doi:10.1007/S42243-020-00362-8 |
| [4] |
Damoah L N W, Zhang L F. High-frequency electromagnetic purification of silicon[J]. Metallurgical and Materials Transactions B, 2015, 46(6): 2514-2528. Doi:10.1007/S11663-015-0447-2 |
| [5] |
Zhang L S, Zhang X F, Wang B, et al. Numerical analysis of the influences of operational parameters on the braking effect of EMBr in a CSP funnel-type mold[J]. Metallurgical and Materials Transactions B, 2014, 45(1): 295-306. Doi:10.1007/S11663-013-9948-z |
| [6] |
王进进, 张杰, 倪明玖. 均匀磁场中初始静止的液态金属在电流作用下三维运动的数值研究[J]. 中国科学院大学学报, 2015, 32(2): 166-171. Doi:10.7523/j.issn.2095-6134.2015.02.004 |
| [7] |
Iwata H, Yamada K, Fujita T, et al. Electromagnetic stirring of molten core in continuous casting of high carbon steel[J]. Transactions of the Iron and Steel Institute of Japan, 1976, 16(7): 374-381. Doi:10.2355/isijinternational1966.16.374 |
| [8] |
Khine Y Y, Walker J S. Thermoelectrically driven melt motion during floating zone crystal growth with an axial magnetic field[J]. Journal of Fluids Engineering, 1998, 120(4): 839-843. Doi:10.1115/1.2820748 |
| [9] |
Farahat R, Eissa M, Megahed G, et al. Effect of EAF slag temperature and composition on its electrical conductivity[J]. ISIJ International, 2019, 59(2): 216-220. Doi:10.2355/isijinternational.isijint-2018-507 |
| [10] |
王璐璐, 周勇军, 鲍苏洋, 等. 改进型INTER-MIG桨搅拌槽内流场的PIV实验[J]. 过程工程学报, 2017, 17(3): 447-452. Doi:10.12034/j.issn.1009-606X.216263 |
| [11] |
谢开旺, 刘明, 刘静, 等. 电磁泵驱动室温金属流体的数值模拟与试验研究[J]. 电子机械工程, 2009, 25(3): 1-5, 23. Doi:10.19659/j.issn.1008-5300.2009.03.001 |
| [12] |
任兵芝, 朱苗勇, 王宏丹, 等. 大方坯连铸结晶器电磁搅拌三维电磁场与流场的数值模拟[J]. 金属学报, 2008, 44(4): 507-512. |
| [13] |
赵菲. 圆坯连铸结晶器电磁搅拌磁场及流场的数值模拟[D]. 秦皇岛: 燕山大学, 2017.
|
| [14] |
Ernst R, Perrier D, Brun P, et al. Multiphase electromagnetic stirring of low conducting liquids[J]. COMPEL-the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2005, 24(1): 334-343. |
| [15] |
李勇. 高频行波磁场增强低电导率液体传输的研究[D]. 北京: 中国科学院大学, 2019.
|
 2023, Vol. 40
2023, Vol. 40 


