2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
近年来,中国自然灾害频繁剧烈,造成严重的经济损失和人员伤亡。灾害场景下的路径规划主要针对人员、移动机器人、无人机等进行物资输送和救援工作,因此对规划路径的距离、平滑性、安全性等具备较高的精度要求。合理且高精度的路径规划算法无疑能最大程度地降低因自然灾害带来的各项损失。
路径规划算法常被应用于移动机器人[1]、无人机[2-6]、人群疏散[7-8]、无线传感网络[9]、B5G/6G[10-11]等领域并发挥重要作用。常见算法包括Dijkstra算法和A*算法,但存在算法复杂度高且不一定能找到最优路径的弊端,神经网络算法存在收敛慢且易收敛到局部最优的弊端。而群智能算法通过个体间相互协作和组织的天然分布式和自组织特性,在路径规划方面表现出更好的收敛速度和寻优能力。常见的群智能算法包括布谷鸟算法、粒子群算法、萤火虫算法、灰狼优化算法、人工蜂群算法[12-14]等。
人工蜂群(artificial bee colony, ABC)算法的性能优于许多其他基于种群的启发式算法[15],但是与开发能力相比,ABC算法更注重探索,导致ABC算法的开发能力差,存在收敛速度慢及易陷入局部最优等弊端[16]。文献[17-18]在初始化阶段生成一般初始化解的基础上,加入了异构的、对称的或对立的解集,增强了ABC算法的全局探索能力,但并没有有效提升收敛速度。Zhang等[15]通过在食物源更新方程中加入自适应步长因子来加快收敛速度,但是自适应步长因子的值随着地图模型的变化而变化,不具备完备性,并且自适应步长的确定需要花费大量的计算资源。文献[19-22]中在食物源更新方程中引入全局最优个体信息来提升收敛速度和精度,但同时也伴随着收敛过快、收敛至局部最优解等弊端。文献[23-24]则分别将ABC算法与概率路线图方法和快速随机搜索树结合来解决收敛速度慢、易陷入局部最优的弊端,但增加了算法复杂度。
通过借鉴先前研究学者研究经验,本文将随机初始化改进为全域采样随机初始化以保证初始解集完备性,并把开采次数加入到选择概率计算中抑制部分局部最优解,提升潜在较优解选中概率,同时根据解在各个维度的开采次数设计全局最优个体引导下的自适应局部开发方程,提升局部开发精度。最后通过在不同灾害场景下与各算法进行仿真对比,改进后的ABC算法具备更优的求解精度以及全局收敛性。
1 ABC算法原理分析ABC算法是一种模拟蜜蜂群体智能搜索行为的生物优化方法。该算法通过3种类型的蜂群相互合作从而寻找到最优蜜源。第1种蜂群是雇佣蜂蜂群,其任务是寻找潜在的解决方案。第2种蜂群是跟随蜂蜂群,其任务是对雇佣蜂所找到的潜在解决方案做进一步精确搜索。第3种蜂群是侦察蜂蜂群,该蜂群通过重新生成新解替代那些陷入局部最优的解决方案,提高ABC算法的全局搜索能力。
ABC算法与大多数仿生学算法类似,主要包含全局探索和局部开发2个过程。初始时随机初始化以及侦察蜂阶段对陷入局部最优个体进行随机初始化主要实现全局探索,公式如下
| $ x_i^j=x^{j_{\min }}+R \times\left(x^{j_{\max }}-x^{j_{\min }}\right). $ | (1) |
式(1)表示第i个个体的第j维度的随机初始化过程,其中R为[0, 1]之间随机数,xjmin和xjmax分别表示第j维度的最小值和最大值。
ABC算法的局部开发主要发生在雇佣蜂阶段以及跟随蜂阶段,开发过程主要通过与一个随机选择的个体进行信息交互完成局部开发,公式如下
| $ x_i^{j *}=x_i^j+R \times\left(x_k^j-x_i^j\right) . $ | (2) |
式(2)表示第i个个体的第j维度进行局部开发的过程,其中k≠i,R∈[-1, 1]。
另外,在跟随蜂阶段的轮盘赌选择前需要评估每一个解的好坏,由于实验采用的是灾害场景模型,故目标函数和适应度值计算如下:
| $ \mathrm{obj}_i=\alpha \times J_{\mathrm{thr}, i}+\beta \times J_{\text {len. } i}+\gamma \times J_{\theta, i}, $ | (3) |
| $ \mathrm{fit}_i=\left\{\begin{array}{cc} 1 /\left(1+\mathrm{obj}_i\right), & \mathrm{obj}_i \geqslant 0, \\ 1+\left|\mathrm{obj}_i\right|, & \mathrm{obj}_i <0 . \end{array}\right. $ | (4) |
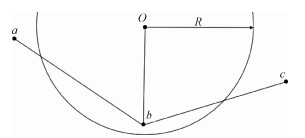
其中: Jthr、Jlen和Jθ分别代表路径危险系数、路径长度和路径平滑因子,α、β和γ为加权系数,用来平衡三者的影响强度。以图 1为例三者的计算如下所示
| $ J_{\operatorname{thr}(b)}=N \times\left(1-L_{o b} / R\right), $ | (5) |
| $ J_{\operatorname{len}(a b)}=L_{a b} /\left(x_b-x_a\right), $ | (6) |
| $ J_{\theta(b)}=\left(\frac{L_{a b}^2+L_{b c}^2-L_{a c}^2}{2 L_{a b} L_{b c}}+1\right) / 2 . $ | (7) |
|
Download:
|
| 图 1 部分路径规划结果 Fig. 1 Screenshot of path planning | |
其中: Lab表示a、b两点间的欧式距离,N为较大值。式(6)中除以横向距离以及式(7)中对计算所得余弦值加1后除以2主要为了实现近似归一化,使距离因子和平滑因子尽可能相近,方便加权系数调整。
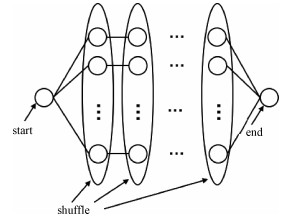
2 改进ABC算法 2.1 小样本初始化在ABC算法中,初始位置需要较强的随机性,同时满足多样性以及遍历性需求。因此将初始化过程按如图 2所示改进,根据每一维度的探索上下限进行等间隔采样,然后随机打乱并进行连接的过程实现初始化,满足小样本在初始化时的随机性,多样性与完备性需求。
|
Download:
|
| 图 2 随机初始化过程 Fig. 2 Random initialization process | |
跟随蜂阶段,ABC算法根据每个食物源的适应度值大小计算相应的选择概率,进而完成轮盘赌选择。但是这样的选择策略仅考虑了适应度值,忽略了ABC算法另一个重要的因子trial即无效开采次数,trial值较大的个体虽然适应度值较大但可能是一个局部最优解,而trial值较小的个体虽然适应度值不高但有可能只是部分维度未开采至最优解附近。因此将概率计算公式更新成如下所示,其中trial为0个体正好等于trial取开采上限lt个体的λ倍,而λ取大于1的较小值,如1.05,1.1等。
| $ \text { fit }^*=\text { fit } \times\left(\mathrm{e}^{- \text {trial } \times \ln (\lambda) / \mathrm{t}}\right) \text {, } $ | (8) |
| $ p_i=\mathrm{fit}_i^* / \sum\limits_j^{\mathrm{SN}} \mathrm{fit}_j^* . $ | (9) |
在ABC算法中,食物源局部开发方程是权衡局部开发和全局收敛性的关键所在,更新方程设计的优劣极大地影响算法的收敛速度和寻优精度。结合文献[20]中GLABC算法的更新方程设计如下所示的全局最优个体gbest引导下的自适应局部更新方程。
| $ \delta=\cos (\pi / 2 \times \boldsymbol{\tau}(i, j) / \mathrm{lt}), $ | (10) |
| $ x_i^j=\text { gbest }_j+\left(x_l^j-x_k^j\right) \times R \times \delta . $ | (11) |
其中:R∈[-1, 1],i≠l≠k。若个体包含维度数为m,则τ代表SN×m大小的矩阵,用来记录每个个体每个维度的开发情况。τ的更新方式与trial一致,当第i个个体的第j维度更新后并不能得到更优的结果时,τ(i, j)加1,否则置0。算法根据个体在该维度的开发情况生成自适应收敛因子δ来实现邻域压缩开发。同时余弦函数在[0, π/2]具备前期下降平缓后期下降较快的特点,正好满足ABC算法前期探索范围大后期精确开发的需求。
2.4 改进ABC算法流程本文提出的改进ABC算法详细步骤如下:
步骤1 算法参数初始化以及蜜源信息初始化,其中包括种群数量SN,无效开采次数上限lt,蜜源初始位置信息等。
步骤2 算法进入雇佣蜂阶段,按式(11)进行邻域开发,并进行贪婪选择,选取较优蜜源,同时更新无效开采次数和τ矩阵。
步骤3 算法进入跟随蜂阶段,按式(9)得到的概率值进行轮盘赌选择,对选中的个体按式(11)进行邻域开发,同时按照贪婪策略选取较优蜜源,同时更新无效开采次数和τ矩阵。
步骤4 算法进入侦察蜂阶段,对无效开采次数大于lt的个体按式(1)进行重新初始化。
步骤5 如果找到最优解或者迭代次数到达上限,转至步骤6,否则转至步骤2。
步骤6 输出路径规划结果。
3 实验与分析为验证改进ABC算法的有效性,将改进ABC算法与标准PSO算法、标准ABC算法、GLABC[20]算法、IABC[3]算法、IFABC[3]算法、NABC[13]算法、BEABC[3]算法进行仿真对比。实验仿真环境为MATLAB R2016b、Core i5、64位Windows操作系统。
3.1 模型参数设置实验中以森林火灾模型下人员及无人机路径规划作为基准模型。如图 3 (a)中2006年四川省木里县依吉火场所示,火场案例主要包括线火场和范围火场两类,其中下侧黑实线为火灾已经扑灭的区域。图 3(b)中使用一系列小圆对线火场进行模拟,较大圆对范围火场进行模拟,同时星号作为路径规划的起点,方框作为路径规划的终点,圆形区域代表危险区域,离中心点越近则危险性越大。通过拟合火灾场景及细微调整生成如图 4所示5种不同复杂程度的灾害模型对算法求解精度、收敛性等进行分析。

|
Download:
|
| 图 3 火灾模型转换示意图 Fig. 3 Fire model conversion diagram | |
|
Download:
|
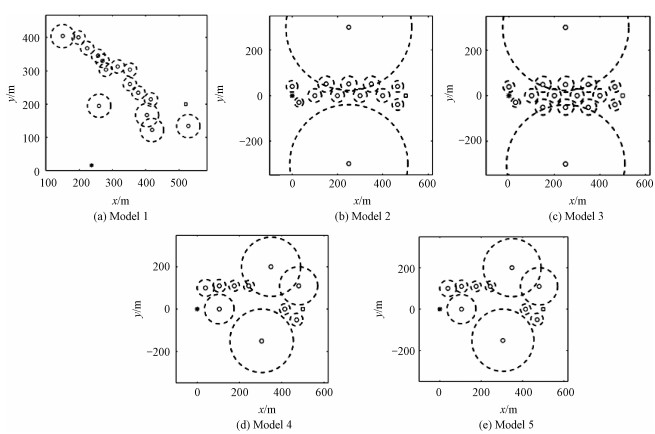
| 图 4 5种不同灾害场景 Fig. 4 Five different disaster scenarios | |
为了客观分析算法性能,所有算法的种群大小均设置为30,最大迭代次数分别为300、500和1 000次,探索维度为30,其中PSO算法的加速常数c1为2.05,加速常数c2为2.05,惯性权重w为0.707 1,改进ABC算法λ为1.1,每组实验均在相同实验环境下运行20次。记录20次实验结果中的最小值、均值、方差以及单次运行耗时作为算法评价指标。
3.2 实验结果与分析模型1~模型5分别对应着5种不同复杂程度的灾害场景。模型1相对简单且最优路径单一,但也极易出现小圆间穿越的不合理规划路径,且路径规划前半段存在较大的安全探索范围,较大的探索范围需要算法较多的迭代次数完成收敛。模型2相对复杂,模型3在模型2基础上改进,进一步增加了模型的复杂度,2种场景均存在较多的局部最优解,需要算法具备较好的局部最优规避能力。模型4和模型5均存在上侧或下侧通过的合理路径,上侧可通行区域较窄,其中模型5属于常见的由较大点火源产生飞火而引发多处产生点火源的场景。
表 1~表 3列出了不同算法在迭代次数为300、500和1 000次下运行20次得到的目标函数的最小值、均值、方差以及单次运行耗时的实验结果。从该实验结果可以看出,在不同场景下,ABC算法在最小值和均值方面的结果都优于PSO算法,方差与PSO算法相近,算法复杂度略高于PSO算法导致算法耗时更长,但ABC算法整体性能更佳。相较于标准ABC算法,各类改进后的ABC算法在最小值和均值方面均取得了更好的结果。在算法迭代初期由于各类改进ABC算法增加额外计算耗时,算法运行耗时有小幅增加,但在迭代后期由于各类算法均具备较好的收敛特性,计算复杂度降低,算法运行耗时与标准ABC算法相近甚至更低。
|
|
表 1 300次迭代下各算法寻优结果 Table 1 Optimization results of each algorithm under 300 iterations |
|
|
表 2 500次迭代下各算法寻优结果 Table 2 Optimization results of each algorithm under 500 iterations |
|
|
表 3 1 000次迭代下各算法寻优结果 Table 3 Optimization results of each algorithm under 1 000 iterations |
本文改进下的ABC算法增加了更新后的适应度值存储矩阵以及每个个体每个维度开发情况的存储矩阵,大小分别为SN×1以及SN×m,其中SN和m分别代表食物源总数与每个食物源包含的维度,均为较小值,并没有增加较多的额外空间。该算法由于初始化时采用全局采样随机化的初始化方式,在Model1和Model5初始化范围较大且迭代次数为300次时效果一般,而GLABC算法在Model1以及NABC在Model2和Model5下取得了更好的实验结果,但是两者在算法迭代中易陷入局部最优或者在局部最优附近浪费过多计算资源。本文改进下的ABC算法虽然采用了与GLABC算法和NABC算法类似的全局最优个体引导下的局部开发,但是加入了与维度开发次数相关的自适应收敛因子,增加了局部开发的精确性,提升了ABC算法的局部开发精度和收敛特性。同时本文提出的算法在选择阶段的选择概率计算中加入了无效开采次数的影响,避免算法在局部最优附近过度开发浪费资源,提升潜在最优解的选中概率。从表 1~表 3可以看出,GLABC算法和NABC算法由于易陷入局部最优或在局部最优附近浪费过多资源的局限性,在迭代1 000次时实验效果远不如本文改进下的ABC算法。而至于IABC算法、IFABC算法以及BEABC算法,虽然具备较好的收敛特性,但由于收敛速度慢以及开发精度低等缺陷,实验效果也不如本文提出的改进ABC算法。同时本文提出的改进ABC算法方差较小具备较好的全局收敛性,算法运行中主要增加了式(8)和式(10)的计算资源消耗,从实验结果的time系数也可以看出并没有明显增加ABC算法的计算复杂度。
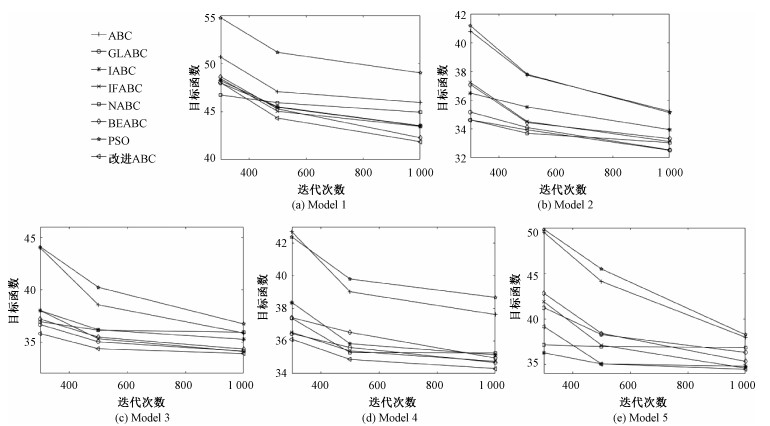
为更加直观地显示各个算法的寻优进程和收敛特性,图 5给出不同模型下各个算法均值的收敛变化曲线。从图中可以看出不同改进ABC算法均较好地提高了ABC算法的实验性能,其中IABC算法、IFABC算法、BEABC算法由于开发精度低导致目标函数值的结果一般,GLABC算法和NABC算法在迭代初期具备较好的实验结果但是收敛速度慢,而本文改进下的ABC算法目标函数值更小且收敛性更好,具备更好的开发精度和收敛特性。
|
Download:
|
| 图 5 5种不同场景下的均值收敛曲线 Fig. 5 Mean convergence curve in five different scenarios | |
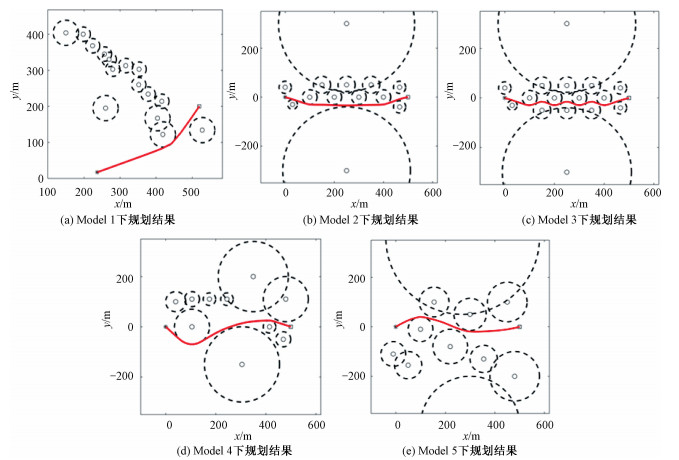
图 6给出了不同灾害模型下改进ABC算法在迭代1 000次后得到的最优路径规划结果。实验结果表明改进后的ABC算法在不同灾害场景下均能较好地规划出安全、移动距离短以及平滑的较优路径。
|
Download:
|
| 图 6 改进ABC算法下路径规划结果 Fig. 6 Path planning results under improved ABC algorithm | |
基于标准ABC算法全局探索能力强,局部开发能力弱的特点提出一种自适应收敛下的改进ABC算法。在初始化阶段采用全域采样随机初始化的方式可以保证初始解的随机性和完整性;开采次数作为信息交互因子加入到选择概率中,抑制局部最优解选中概率,提升潜在较优解选中概率;根据每个解在每个维度的开发次数设计全局最优个体引导下的自适应局部开发方程,提升局部开发精度。最后的仿真结果表明改进ABC算法具备更优的算法求解精度以及全局收敛性,能够更好地解决复杂灾害场景下的路径规划问题。
| [1] |
Li X M, Huang Y H, Zhou Y J, et al. Robot path planning using improved artificial bee colony algorithm[C]//2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC). October 12-14, 2018, Chongqing, China. IEEE, 2018: 603-607. DOI: 10.1109/IAEAC.2018.8579242.
|
| [2] |
Li B, Chiong R, Lin M. A two-layer optimization framework for UAV path planning with interval uncertainties[C]//2014 IEEE Symposium on Computational Intelligence in Production and Logistics Systems (CIPLS). December 9-12, 2014, Orlando, FL, USA. IEEE, 2014: 120-127. DOI: 10.1109/CIPLS.2014.7007170.
|
| [3] |
Li B, Gong L G, Yang W L. An improved artificial bee colony algorithm based on balance-evolution strategy for unmanned combat aerial vehicle path planning[J]. The Scientific World Journal, 2014, 2014: 232704. Doi:10.1155/2014/232704 |
| [4] |
Li B, Gong L G, Zhao C H. Unmanned combat aerial vehicles path planning using a novel probability density model based on Artificial Bee Colony algorithm[C]//2013 Fourth International Conference on Intelligent Control and Information Processing (ICICIP). June 9-11, 2013, Beijing, China. IEEE, 2013: 620-625. DOI: 10.1109/ICICIP.2013.6568149.
|
| [5] |
Murrieta-Mendoza A, Botez R M, Bunel A. Four-dimensional aircraft en route optimization algorithm using the artificial bee colony[J]. Journal of Aerospace Information Systems, 2018, 15(6): 307-334. Doi:10.2514/1.1010523 |
| [6] |
Tian G Z, Zhang L, Bai X, et al. Real-time dynamic track planning of multi-UAV formation based on improved artificial bee colony algorithm[C]//2018 37th Chinese Control Conference (CCC). July 25-27, 2018. Wuhan. IEEE, 2018: 10055-10060.
|
| [7] |
Liu H, Xu B, Lu D J, et al. A path planning approach for crowd evacuation in buildings based on improved artificial bee colony algorithm[J]. Applied Soft Computing, 2018, 68: 360-376. Doi:10.1016/j.asoc.2018.04.015 |
| [8] |
Patle B K, Babu L G, Pandey A, et al. A review: on path planning strategies for navigation of mobile robot[J]. Defence Technology, 2019, 15(4): 582-606. Doi:10.1016/j.dt.2019.04.011 |
| [9] |
Ren G, Wu J B, Versonnen F. Bee-based reliable data collection for mobile wireless sensor network[J]. Cluster Computing, 2019, 22(4): 9251-9260. Doi:10.1007/s10586-018-2116-0 |
| [10] |
Zhou Y Q, Liu L, Wang L, et al. Service-aware 6G: an intelligent and open network based on the convergence of communication, computing and caching[J]. Digital Communications and Networks, 2020, 6(3): 253-260. Doi:10.1016/j.dcan.2020.05.003 |
| [11] |
Zhou Y Q, Tian L, Liu L, et al. Fog computing enabled future mobile communication networks: a convergence of communication and computing[J]. IEEE Communications Magazine, 2019, 57(5): 20-27. Doi:10.1109/MCOM.2019.1800235 |
| [12] |
Li Z Y, Zhang Z, Liu H, et al. A new path planning method based on concave polygon convex decomposition and artificial bee colony algorithm[J]. International Journal of Advanced Robotic Systems, 2020, 17(1): 172988141989478. Doi:10.1177/1729881419894787 |
| [13] |
Gao W F, Liu S Y, Huang L L. A novel artificial bee colony algorithm based on modified search equation and orthogonal learning[J]. IEEE Transactions on Cybernetics, 2013, 43(3): 1011-1024. Doi:10.1109/TSMCB.2012.2222373 |
| [14] |
Zhang H Y, Lin W M, Chen A X. Path planning for the mobile robot: a review[J]. Symmetry, 2018, 10(10): 450. Doi:10.3390/sysm10100450 |
| [15] |
Zhang Q, Wei S, Xue M, et al. A variable-step two synchronous artificial bee colony algorithm for mobile robot path planning[C]//2018 Chinese Automation Congress (CAC). November 30-December 2, 2018, Xi'an, China. IEEE, 2018: 2054-2058. DOI: 10.1109/CAC.2018.8623333.
|
| [16] |
刘东林, 陈银银. 基于花香浓度的人工蜂群算法在机器人路径规划中的应用[J]. 华东理工大学学报(自然科学版), 2016, 42(3): 375-381. Doi:10.14135/j.cnki.1006-3080.2016.03.013 |
| [17] |
Gao W F, Liu S Y. A modified artificial bee colony algorithm[J]. Computers & Operations Research, 2012, 39(3): 687-697. Doi:10.1016/j.cor.2011.06.007 |
| [18] |
Wang J C, Sun Y H, Liu F X. An improved double-population artificial bee colony algorithm based on heterogeneous comprehensive learning[J]. Soft Computing, 2018, 22(19): 6489-6514. Doi:10.1007/s00500-017-2700-x |
| [19] |
Singh A, Deep K. Artificial bee colony algorithm with improved search mechanism[J]. Soft Computing, 2019, 23(23): 12437-12460. Doi:10.1007/s00500-019-03785-y |
| [20] |
Lu R, Hu H D, Xi M L, et al. An improved artificial bee colony algorithm with fast strategy, and its application[J]. Computers & Electrical Engineering, 2019, 78: 79-88. Doi:10.1016/j.compeleceng.2019.06.021 |
| [21] |
Yi Y, He R J. A novel artificial bee colony algorithm[C]//2014 Sixth International Conference on Intelligent Human-Machine Systems and Cybernetics. August 26-27, 2014, Hangzhou, China. IEEE, 2014: 271-274. DOI: 10.1109/IHMSC.2014.73.
|
| [22] |
Xu F Y, Li H L, Pun C M, et al. A new global best guided artificial bee colony algorithm with application in robot path planning[J]. Applied Soft Computing, 2020, 88: 106037. Doi:10.1016/j.asoc.2019.106037 |
| [23] |
Alpkiray N, Torun Y, Kaynar O. Probabilistic roadmap and artificial bee colony algorithm cooperation for path planning[C]//2018 International Conference on Artificial Intelligence and Data Processing (IDAP). September 28-30, 2018, Malatya, Turkey. IEEE, 2018: 1-6. DOI: 10.1109/IDAP.2018.8620808.
|
| [24] |
Yue T S, Chung H Y. Using ABC and RRT algorithms to improve mobile robot path planning with danger degree[C]//2016 Fifth International Conference on Future Generation Communication Technologies (FGCT). August 17-19, 2016, London, UK. IEEE, 2016: 21-26. DOI: 10.1109/FGCT.2016.7605068.
|
 2023, Vol. 40
2023, Vol. 40 


