2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
随着供电需求的增大和技术的发展,电网的容量在不断增加,维护和检测的成本也不断提高。因此,在变电站或输电线路上建立各类检测系统,通过传感器收集各类环境信息,数据经由无线网络传到监测平台,做到无人值守,实时监控,可以很大地节约成本。无线传感器网络(wireless sensor network,WSN)[1]具有自组织、低功耗、高鲁棒性的特点,适用于输变电场景监测区域广、传感器众多的特点。WSN中的传感器通常由电池供电[2],且难以更换,能耗是主要研究的一个问题。
针对这一问题,许多学者做了大量的研究。LEACH(low-energy adaptive clustering hierarchy)是由Heinzelman等[3]提出的基于分簇的路由协议,网络中的节点随机选出簇首,其他节点选择簇首加入簇中,以此延长网络生命周期。但是,LEACH随机选举簇首,没有考虑到节点能耗问题和位置因素,并且簇首到基站为单跳传输。对于上述问题,后来的学者从这几个方面做了很多改进,Heinzelman等[4]考虑了剩余能量的问题,又提出LEACH-C选择能量值高于平均能量的节点作为簇首的候选节点; 黄利晓等[5]提出LEACH-improved加入距离因子和能量密度等因素去选举簇首;Hu和Wang[6]提出EEUC,采用簇间多跳和非均匀分簇的方式,均衡了能耗;Lee和Kao[7]在分簇算法中引入边缘度和双能量阈值的算法考虑了各类节点的位置信息,同时对剩余能量的选择进行优化;李安超和陈桂芬[8]提出一种3层结构的分簇算法,改进了分簇的模型,适用于大规模的无线传感器网络。同时,汇聚节点移动也作为一种平衡能耗的改进方式,Gharaei等[9]采用移动汇聚节点的方法,并使用人工蜂群优化算法规划了最优路径,但并不适用于常处于室外或布线复杂的输变电环境。群智能算法作为优化多峰函数的算法,一些学者在簇首选举的过程中引入了群智能算法,Daneshvar等[10]使用灰狼优化算法选举簇首,提出双跳路由算法,均衡了能耗、戴剑勇等[11]引入萤火虫算法和BP神经网络,考虑了簇首密度、簇首位置,对簇首选举和路径选择进行优化;Singh等[12]引入粒子群算法,改善簇首分布不均的问题;武小年等[13]提出改进粒子群优化算法的分簇路由协议,把节点的剩余能量和位置因子作为粒子群优化算法的目标,通过自适应学习因子对粒子群优化算法做了改进。麻雀搜索算法(sparrow search algorithm,SSA)是由Xue和Shen[14]提出的一种模拟麻雀觅食和警戒行为的智能算法,在高维多峰的优化上其求解成功率、收敛速度等方面表现优异,已应用于图像分割[15]、三维无人机航空优化[16]等场景。而输变电场景中节点个数众多,对于最优簇首集合的选举问题,SSA算法寻优精度高,具有一定优势,并且尚未应用在簇首选举当中。
在输变电的部分场景,如大型室外变电站,监测区域大,传感器众多,难以供电,为了节约成本,传感器的计算能力较低,不具有组网能力,无法成为“簇首节点”或中继节点,只能以单跳的方式传输进行数据传输。根据上述场景,提出一种解决方案,布置计算能力较高的节点作为传感器的中继节点,中继节点进行组网,并选举出一个节点作为整个网络的网关,称为“无线网关”(wireless gateway),传感器传输数据到中继节点,中继节点收集数据后,进行数据融合,通过中继节点网络传输到无线网关节点,无线网关节点以无线的方式(如4G模块)将数据传输到监测平台。中继节点近似于常见无线传感器网络中的汇聚节点[17](sink node),具有以下功能:1)与传感器通信;2)传输数据到监测平台。输变电场景中,传输数据到监测平台的功能通常由4G模块完成,4G模块会定时向监测平台发送心跳和数据,产生的能耗较大,大于相同时间下与单个传感器通信产生的能耗。而中继节点间也可以通过与传感器通信的方式进行组网,并且产生的能耗会小于节点直接传输数据到监测平台的能耗。因此,本文主要研究的内容为中继节点间的组网,提出一种轮换无线网关节点的路由协议(LEACH-WGR-SSA),防止无线网关节点过早死亡,并对无线网关节点的选举进行优化。在LEACH的基础上考虑了剩余能量、邻接节点个数和位置信息,并引入麻雀搜索智能优化算法对簇首选举进行优化,同时,为避免SSA陷入局部收敛,加入Levy飞行策略,获得了较优的簇首分布,延长了网络生存周期。
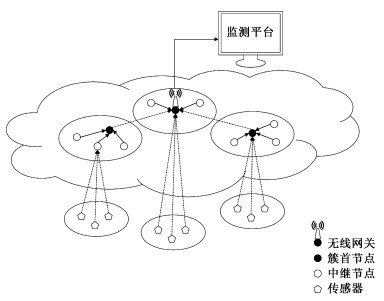
1 网络模型在输变电场景中,大部分场景处于室外或因布线复杂,节点均由电池供电。与常见无线传感器网络的不同,本文中的网络不包含能量无限的汇聚节点,所有中继节点均可与传感器通信,并具有与监测平台通信的功能,选举出的无线网关节点将数据传输到监测平台,其余中继节点关闭该功能。图 1中的传感器收集完变电站或输电线路的环境信息后,接入到中继节点。中继节点之间进行组网,网络每一轮先在中继节点中选举出无线网关,再选举出中继节点的簇首节点,普通的中继节点选择加入到最近的簇中。中继节点收集完传感器的信息后,将数据传输到簇中的簇首节点,簇首节点再将数据传输到无线网关。随后,无线网关将整个网络的信息上传到监测平台。本文的主要研究内容为中继节点的组网和对应的路由算法,暂不考虑传感器的接入。
|
Download:
|
| 图 1 输变电网络结构组成 Fig. 1 Network structure of power transmission and substation | |
本文对输变电网络抽象并假设:网络中有N个中继节点,随机分布在M×M的监测区域,节点不会移动,节点初始能量相同,都具有位置信息、全局唯一ID、计算能力和数据融合能力,数据传输到监测平台会产生一定的能耗。
由于变电站或者输电线路监测场景较大,如大型的室外变电站或者是多条输电线路的交汇处,需要覆盖的区域相对较大,因此,本文仿真选择400 m×400 m的监测区域。并且,输变电场景中传感器众多,为减低能耗,通常通信半径较小,仿真中设置传感器的通信半径20 m,根据正六边形镶嵌模型[18]计算出中继节点最少为156个,但是中继节点为随机放置,为保证对传感器的全覆盖,同时也为了降低死亡节点对覆盖率的影响,设置200个中继节点在监测场景当中。
组网过程将通过网络初始化阶段、无线网关节点选举阶段、簇首选举及分簇阶段和路由传输阶段4部分完成。
2 LEACH-WGR-SSA算法 2.1 网络初始化阶段中继节点部署后,将进行网络初始化。首次建网将预设一个中继节点作为前无线网关节点。各个节点将自己的全局ID、剩余能量、地理位置等报文发送给前无线网关。在完成无线网关的选举或簇首的选举后,广播计算结果,所有节点收到选举结果信息。
2.2 无线网关节点选举阶段为均衡能耗,无线网关节点采用轮换的方式,前无线网关节点对收集的数据进行整合,进行无线网关节点的选举。提出一种算法WGR(wireless gateway rotation),用于无线网关节点的选举,考虑3个主要因素:
1) 中继节点的剩余能量:无线网关节点选举完成后,这个网络将进行分簇,无线网关节点也作为一个簇首。因此,无线网关节点的功能主要为以下3个:接收分簇后簇首的数据,接收簇内节点的数据,传输数据到监测平台。无线网关节点产生的能耗远高于其他节点,因此,选择剩余能量较高的节点作为无线网关节点,防止过早死亡。
2) 中继节点邻接节点数量:无线网关节点也作为一个簇首,接收普通中继节点的数据,邻接节点单跳传输到簇首产生的能耗较小,因此考虑邻接节点的个数作为选举无线网关节点的一个因素。其中节点i的邻接节点集合表示为
| $ G_i=\left\{j \mid d(i, j) \leqslant R, j \in G_{\text {alive }}\right\}, i \in G_{\text {alive }}, $ | (1) |
| $ R=\frac{M}{\sqrt{N \times p \times \pi}}. $ | (2) |
其中:d(i, j)为节点i和节点j之间的距离,R为邻接节点的范围半径,N为节点数量,M为监测区域变长,p为簇首节点和无线网关在所有节点中的占比,Galive是存活节点的集合。
3) 中继节点到所有存活节点质心的距离:为保证整个网络能量负载的均衡,将无线网关节点放置于中心的位置可以减少平均的传输距离和跳数,因此,将中继节点到所有存活节点质心的距离作为一个考虑因素。
pWG(i)为无线网关节点选举的权值函数:
| $ \begin{gathered} p_{\text{WG}}(i)=\alpha \frac{E_{\text {node }}(i)}{E\left(E_{\text {node }}\right)}+\beta \frac{N_{\text {neighbor }}(i)}{E\left(N_{\text {neigbor }}\right)}+ \\ \delta \frac{d_{\text {toCT }}(i)}{E\left(d_{\mathrm{toCT}}\right)}, i \in G_{\text {alive }} . \end{gathered} $ | (3) |
| $ E\left(E_{\text {node }}\right) =\frac{1}{n}\left(\sum\limits_{i \in G_{\text {alive }}} E_{\text {node }}(i)\right) . $ | (4) |
| $ E\left(N_{\text {neighbor }}\right) =\frac{1}{n}\left(\sum\limits_{i \in G_{\text {alive }}} N_{\text {neighbor }}(i)\right) . $ | (5) |
| $ E\left(d_{\mathrm{toCT}}\right) =\frac{1}{n}\left(\sum\limits_{i \in G_{\text {alive }}} d_{\mathrm{toCT}}(i)\right). $ | (6) |
其中:α+β+δ=1,α, β, δ∈(0, 1);Enode(i)是i节点的剩余能量;E(Enode)是节点平均剩余能量;Nneighbor(i)是i节点的邻接节点个数;E(Nneigbor)为所有存活节点平均的邻接节点数;dtoCT(i)是节点i距离存活节点集合质心的距离;E(dtoCT)是所有存活节点距离存活节点集合质心的距离平均值;n为所有存活节点个数;Galive是存活节点的集合。
| $ i_{\text {opt }} \in \max \left(p_{\text {WG }}(i), i \in G_{\text {alive }}\right) . $ | (7) |
编号为iopt的节点成为无线网关节点,无线网关节点选举完成。
α,β,δ的选择对仿真的结果有重要的影响。其中α为中继节点剩余能量因子的加权因子,在整个网络的初期,各个节点剩余能量较多,对能量的敏感度较小,因此前期选择降低剩余能量因子。网络传输到达一定的时间,各个节点的剩余能量所剩不多,容易死亡,因此剩余能量对网络生命周期影响较大,应提高α的大小。β为中继节点邻接节点数量因子的加权因子,对于分布不均匀的网络,可以提高该因子。δ为中继节点到所有存活节点质心距离的加权因子,该因子影响这个网络的平均传输距离,影响着每一轮的传输能耗,对于节点剩余能量较少的情况,为减少节点的死亡速度,均衡能耗,α重要性要高于δ。多次实验表明:在节点总剩余能耗减少一半之前,设置α为0.3,β为0.2,δ为0.5;节点总能耗减少一半后,设置α为0.6,β为0.2,δ为0.2,仿真结果较优。本文的仿真使用上述的参数和方法。
2.3 簇首选举及分簇过程无线网关节点选举完成后,整个网络的结构与常见的传感器网络类似,采用分簇路由机制可以均衡网络的能耗,防止无线网关周围的“热点节点”迅速死亡。
前无线网关节点选择簇首并建立分簇。本文采用麻雀搜索算法对簇首的分布进行优化,优化目标为提高簇首节点的剩余能量在所有存活节点中的占比,减少每轮传输的能耗。并且为加速收敛,对种群初始化进行优化,考虑3个因素:中继节点的剩余能量、中继节点邻接节点数、到无线网关节点的距离。虽然SSA具有强大的局部搜索能力,但与多种群智能优化算法类似,容易陷入局部最优,因此,使用Levy飞行策略进行改进。
2.3.1 麻雀搜索算法该算法主要分为以下几个步骤:
1) 种群初始化
| $ \boldsymbol{X}=\left[\begin{array}{cccc} X_1^1 & X_1^2 & \cdots & X_1^{d_{\text {pop }}} \\ X_2^1 & X_2^2 & \cdots & X_2^{d_{\text {pop }}} \\ \cdots & \cdots & \cdots & \cdots \\ X_{N_{\text {pop }}}^1 & X_{N_{\text {pop }}}^2 & \cdots & X_{N_{\text {pop }}}^{d_{\text {pop }}} \end{array}\right] \text {. } $ | (8) |
| $ \begin{gathered} X_j^i=L_{\mathrm{B}}(i)+w_j^i \times\left(U_{\mathrm{B}}(i)-L_{\mathrm{B}}(i)\right), \\ i \in\left[1, d_{\mathrm{pop}}\right], j \in\left[1, N_{\text {pop }}\right] . \end{gathered} $ | (9) |
其中,Npop为种群数量,dpop为优化的维数,LB,UB为参数的下界和上界,wji为0到1的随机变量。
2) 计算适应度函数
适应度函数是智能优化算法不断迭代优化的指标。定义适应度函数为
| $ F(i)=f\left(\left[\begin{array}{llll} X_i^1 & X_i^2 & \cdots & X_i^{d_{\text {pop }}} \end{array}\right]\right), i \in\left[1, N_{\text {pop }}\right] . $ | (10) |
其中, f(x)为每个种群向量的适应度函数。根据适应度对种群i进行排序。
3) 更新发现者位置
算法中包含3个角色: 发现者、加入者和警戒者。发现者和加入者是可以相互转化的,但是总比例不变。发现者负责觅食并为加入者找到寻优方向,发现者更新的公式如下
| $ X_j^i(t+1)=\left\{\begin{array}{c} X_j^i(t) \cdot \exp \left(-\frac{i}{\mu \cdot T}\right), V<S_{\mathrm{T}}, \\ X_j^i(t)+Q \cdot \boldsymbol{W}, V \geqslant S_{\mathrm{T}} . \end{array}\right. $ | (11) |
其中:t为当前迭代次数,Xji(t)为j种群i元素的t次数下的参数。T为总迭代次数。μ为0到1的随机值,V(V∈[0, 1]),ST(ST∈[0.5, 1])为预警值和安全值,Q为正态分布的随机数,W为1×dpop的全1矩阵。V < ST代表发现者处于安全位置,进而进行大范围搜索。反之,表示发现了危险,去其他位置进行搜索。
4) 更新加入者位置
加入者的更新公式为
| $ \begin{gathered} X_j^i(t+1)= \\ \left\{\begin{array}{l} Q \cdot \exp \left(-\frac{X_{\text {worst }}(t)-X_j^i(t)}{i^2}\right), i>\frac{N_{\text {pop }}}{2}, \\ X_{\text {best }}(t+1)+\left|X_j^i(t)-X_{\text {best }}(t+1)\right| \cdot \\ \boldsymbol{A}^{+} \cdot \boldsymbol{W}, i \leqslant \frac{N_{\text {pop }}}{2} . \end{array}\right. \end{gathered} $ | (12) |
其中: Xbest为当前最优位置,Xworst为最差位置; A+为1×dpop的矩阵,矩阵的值为1和-1随机分布,并且满足A+=AT(AAT)-1。当i > Npop/2时,表示未获得食物,将会去其他位置搜索。
5) 更新警戒者位置
警戒者的更新公式为
| $ X_j^i(t+1)=\left\{\begin{array}{l} X_{\text {best }}(t)+\chi \cdot\left|X_j^i(t)-X_{\text {best }}(t)\right|, \\ \ \ f_i>f_g, \\ X_j^i(t)+H \cdot\left(\frac{\left|X_j^i(t)-X_{\text {worst }}(t)\right|}{\left(f_i-f_w\right)+\varepsilon}\right), \\ \ \ f_i=f_g . \end{array}\right. $ | (13) |
其中: χ~N(0, 1)作为步长,H为-1到1的随机数;fi,fw,fg分别为当前种群麻雀的适应度值,当前最差的适应度值和最佳的适应度值。fi > fg表示麻雀在整个种群中处于较差的位置;fi=fg表示麻雀意识到危险,靠近其他的麻雀。
6) 迭代并更新位置
重复步骤3)~步骤5)直至低于阈值或达到迭代次数。
2.3.2 Levy飞行策略优化Levy飞行属于马尔可夫过程,这是一种特殊的随机游走策略,它结合了短距离搜索和偶尔的跳远。因此,Levy飞行策略[19]可以增加种群的多样性。Levy飞行策略遵循如下公式
| $ L(S) \sim|S|^{-1-\eta}(0<\eta<2) . $ | (14) |
由于其分布较为复杂,常使用Mantegna算法进行模拟。
| $ S=\frac{\theta}{|\omega|^{1 / \eta}}, \theta \sim N\left(0, \delta_u^2\right), \omega \sim N\left(0, \delta_v^2\right) . $ | (15) |
| $ \delta_u=\left(\frac{\tau(1+\eta) \sin (\pi \eta / 2)}{2^{(\eta-1) / 2} \tau[(1+\eta) / 2] \eta}\right)^{1 / \eta} . $ | (16) |
| $ \delta_v=1 . $ | (17) |
其中:S为随机步长,θ和ω服从正态分布,τ为标准gamma函数。
由于发现者经常引导其他麻雀对位置进行更新,而实验表明,Levy飞行对其他的角色影响很小,因此只使用Levy飞行策略用来更新发现者的位置。
将公式(11)更新为
| $ X_j^i(t+1)=\left\{\begin{array}{l} X_j^i(t) \cdot \exp \left(-\frac{i}{\mu \cdot T}\right)+\xi \cdot L(S) , \\ V<S_{\mathrm{T}}, \\ X_j^i(t)+Q \cdot \boldsymbol{W}+\xi \cdot L(S), V \geqslant S_{\mathrm{T}}. \end{array}\right. $ | (18) |
| $ \xi=0.02\left(X_j^i(t)-X_{\text {best }}\right) \text {. } $ | (19) |
其中ξ为步长。2.3.1中步骤3)中式(11)更为式(18)。
2.3.3 簇首选举簇首选举过程按照麻雀搜索的优化算法的步骤进行:
1) 种群初始化
为均衡能耗并加速智能算法的收敛,对种群初始化阶段进行优化,将考虑3个因素:节点的剩余能量、节点到基站的距离、节点的邻接节点的个数。与上文无线网关节点选举类似:
| $ \begin{aligned} p_{\text {cluster }}(i) & =o \frac{E_{\text {node }}(i)}{E\left(E_{\text {node }}\right)}+\rho \frac{N_{\text {neighbor }}(i)}{E\left(N_{\text {neigbor }}\right)}+ \\ & v \frac{d_{\text {toWG }}(i)}{E\left(d_{\text {toWG }}\right)}, i \in G_{\text {node }} . \end{aligned} $ | (20) |
| $ E\left(d_{\mathrm{toWG}}\right)=\frac{1}{n}\left(\sum\limits_{i \in G_{\text {node }}} d_{\mathrm{toWG}}(i)\right). $ | (21) |
其中:ο+ρ+υ=1,ο, ρ, υ∈(0, 1);Enode(i)是i节点的剩余能量,E(Enode)是节点平均剩余能量;Nneighbor(i)是i节点的邻接节点个数,E(Nneigbor)为所有存活普通节点平均的邻接节点数;dtoWG(i)是节点i距离无线网关节点的距离,E(dtoWG)是所有存活普通节点距离无线网关节点的距离平均值;Gnode是普通节点的集合。pcluster(i)是簇首的选举公式。
根据pcluster(i)对节点由大到小排序,选择前50%的节点作为候选节点。对于每一个种群从候选节点随机取出不重复的K个值,作为单个种群的一个向量。构建种群初始值之后,为了防止局部最优,将UB、LB即节点编号的上下界,设置为整个存活节点的编号区间。其中根据文献[20],较优的簇首个数为
| $ K=\frac{\sqrt{2}+\ln (1+\sqrt{2})}{6} \sqrt{\frac{\varepsilon_{\mathrm{fs}} n M^2}{\varepsilon_{\mathrm{mp}} d_{\mathrm{toWG}}^4-E_{\text {elec }}}} . $ | (22) |
其中:n为存活节点个数,εfs和εmp分别为自由空间模型和多路衰减模型的功放因子参数,M为监测区域边长,Eelec为电路损耗能量,dtoWG为节点到无线网关的距离期望[21]。
2) 计算适应度函数
适应度函数的确定是算法中最为重要的步骤,不断迭代得到较低的适应度值是麻雀寻优算法的优化目标。选举簇首的优化目标有以下3个:
① 提高簇首节点的剩余能量占所有存活节点的比例:为防止节点迅速死亡,簇首节点应具有较高的能耗,因此,定义能量适应度函数为
| $ f_1=\frac{\sum\limits_i^n E_{\text {node }}(i)}{\sum\limits_i^K E_{\mathrm{CH}}(i)} . $ | (23) |
其中:Enode为普通节点的能量,ECH为簇首节点的能量。
② 降低簇内数据传输的能耗:簇内数据传输的能耗与簇内节点到簇首的距离正相关,因此,定义簇间距离的适应度函数为
| $ f_2=\max \limits_{j=1, 2, \cdots, K}\left(\sum\limits_i^{n(j)} \frac{d(j, i)}{n_c(j)}\right) . $ | (24) |
其中:d(j, i)表示第j个簇中第i个节点到簇首的距离,nc(j)表示第j个簇内的节点个数。
③ 降低簇间数据传输的能耗:簇首间传输数据的能耗与到无线网关节点的距离正相关,因此,定义距离无线网关节点距离的适应度函数为
| $ f_3=\frac{\sum\limits_{i=1}^K d_{\mathrm{toWG}}(i)}{K}. $ | (25) |
其中:dtoWG(i)为第i个簇首到无线网关节点的距离。因此适应度函数为
| $ F=\phi f_1+\varphi f_2+\gamma f_3 . $ | (26) |
其中:ϕ,φ,γ为3类适应度函数的权重,ϕ+φ+γ=1,ϕ, φ, γ∈(0, 1)。计算每个种群的适应度值,进行排序。
ϕ,φ,γ这3个权重对仿真有重要的影响,与无线网关的选举类似,经过多次试验,对这3个参数的选择采取以下策略:设置ϕ为0.3,φ为0.5,γ为0.2;节点总能耗减少一半后,设置ϕ为0.5,φ为0.3,γ为0.2。
3) 更新位置
按照2.3.1中步骤3)~步骤6)进行。
4) 选出簇首
迭代完成后,选出较优的簇首。
本文提出的SSA簇首选举的算法框架如表 1所示。
|
|
表 1 SSA簇首选举算法框架 Table 1 SSA cluster head election algorithm framework |
簇首选举完成后,前无线网关节点通过广播的方式通知所有节点新的无线网关节点和簇首。普通节点选择距离最近的簇首或无线网关节点进行接入。
2.4 路由传输阶段簇内节点通过单跳的方式将数据传输到簇首,簇首对数据进行数据融合。如果簇首距离无线网关节点过远,会产生大量的能耗,因此,采用簇首间多跳的方式传输数据。簇首和无线网关节点按照prim算法计算最小生成树,无线网关节点作为根节点。
考虑到簇首间的传输能耗和剩余能量,防止中继节点能耗过低还要承担转发的能耗。因此,定义簇首间的权值为
| $ w(i, j)=\frac{E_{T \mathrm{x}}(i, j)}{\kappa E_{\text {node }}(i)+(1-\kappa) E_{\text {node }}(j)}, \kappa \in(0, 1) . $ | (27) |
其中:ETx(i, j)为i传输到j的能量;Enode(i),Enode(j)为节点i,j的剩余能量。按照该权值构成簇首间的生成树。
3 仿真与结果分析 3.1 能耗模型本文采用LEACH的能耗模型,根据不同的距离采用自由空间模型或多路衰减模型。其中d为节点间的距离,k为一组数据的比特数,d0为距离门限,εfs和εmp分别为自由空间模型和多路衰减模型的功放因子参数,Eelec为每传输1 bit数据产生的能耗,EDA为每融合1 bit数据的能耗,距离为d传输kbit数据的发送能耗和接收能耗分别为ETx(k, d)和ERx(k),融合kbit的融合能耗为分别为:
| $ E_{\mathrm{Tx}}(k, d)=\left\{\begin{array}{l} k E_{\text {elec }}+k \varepsilon_{\mathrm{fs}} d^2, d<d_0, \\ k E_{\text {elec }}+k \varepsilon_{\mathrm{mp}} d^4, d \geqslant d_0. \end{array}\right. $ | (28) |
| $ E_{\mathrm{Rx}}(k)=k E_{\mathrm{elec}} . $ | (29) |
| $ E_{\mathrm{DA}}(m)=m E_{\mathrm{DA}} . $ | (30) |
| $ d_0=\sqrt{\frac{\varepsilon_{\mathrm{fs}}}{\varepsilon_{\mathrm{mp}}}} . $ | (31) |
仿真初始化的过程中,传输自身剩余能量和位置信息大小为200 bit,无线网关广播的无线网关选举结果的信息大小为100 bit,广播簇首选举结果信息大小为200 bit,无线网关广播的距离为覆盖所有节点的最大半径。
无线网关传输数据到检测平台每一轮的能耗同样满足上述的能耗模型,仿真中,假设每隔200 m存在一个基站用来接收无线网关的数据,设置无线网关上传经过数据融合的数据的大小为4 000 bit,传输半径为200 m,计算出无线网关传输到监测平台每轮传输能耗为8.52×106 nJ。
3.2 仿真结果分别使用LEACH,LEACH-WGR,LEACH-WGR-SSA,LEACH-WGR-PSO等4种算法在相同参数下进行模拟。PSO算法作为群智能优化算法,被多位学者引入到分簇路由算法当中,比较适用于输变电场景监测区域大,节点数量多的特点,因此选择PSO算法进行对比。本文使用网络模型与常用模型有所不同,通常LEACH算法中汇聚节点位置不变且能量无限,本文对应的无线网关节点能量有限、可以轮转,并且会产生传输数据到监测平台的能耗。因此,本文基于LEACH的仿真,对于无线网关节点的处理为随机选举。网络的相关实验环境和参数设置如表 2所示。
|
|
表 2 仿真参数表 Table 2 Simulation parameters |
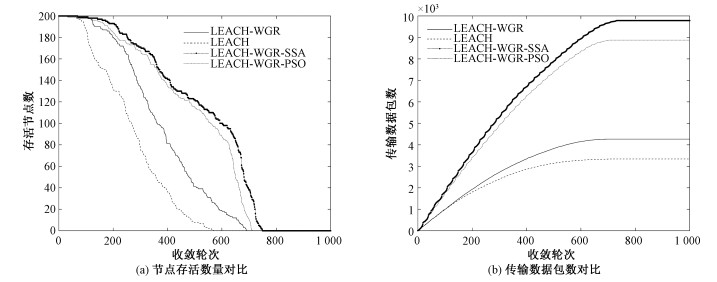
表 3和图 2(a)为4种算法下节点死亡率的对比。仿真结果表明,当50%的节点死亡时,LEACH-WGR的轮数相较于LEACH延长35.1%。同时,采用麻雀搜索算法优化的LEACH-WGR-SSA相较于LEACH和LEACH-WGR提高121.6%和64.1%,比同类智能算法PSO(粒子群优化算法)增加6.5%,延长了业务较多的网络前期,从而增加了整个网络的业务量。WGR的算法综合考虑到无线网关节点的剩余能量、地理位置及邻接节点个数,减少了整个网络传输的距离和跳数,均衡了能耗,减缓了节点的死亡。采用麻雀搜索算法对簇首选举进行优化,在种群初始化和适应度函数的选取上,均考虑了剩余能量因素、簇内节点传输距离和到无线网关节点的距离,做到减少每轮传输的能耗和能量的均衡,同时麻雀搜索算法通过警戒和发现的模式,加入一些扰动,同时加入Levy飞行策略,避免寻优过程陷入局部最优,得到了较好的适应度值。
|
|
表 3 节点死亡率表 Table 3 Percentage death nodes |
|
Download:
|
| 图 2 节点存活数量和传输数据包数对比 Fig. 2 Comparison of number of alive nodes and transmission data among algorithms | |
LEACH-WGR延长了网络的生存周期,相较于LEACH、LEACH-WGR、LEACH-WGR-PSO分别延长31.3%、8.5%、5.3%。相较于常见的无线传感器网络,增长效果有限,因为无线网关传输数据到监测平台每轮的损耗较高,即使进行了优化,节点的每轮能量损耗是固定的,过高的能耗导致节点的迅速死亡。
图 2(b)为传输数据包数的对比。当网络运转结束,LEACH、LEACH-WGR、LEACH-WGR-PSO、LEACH-WGR-SSA传输的数据包数分别为3 339、4 267、8 878、9 788,LEACH-WGR-SSA相较于其他算法提高了193.1%、129.4%、10.3%,LEACH-WGR-SSA传输的包数远高于LEACH和LEACH-WGR。说明LEACH-WGR-SSA算法的能量效率较高,每轮数据传输的能量较少,能量分配均衡,存活的节点越多,传输的数据也就越多。
图 3为LEACH-WGR-PSO和LEACH-WGR-SSA在相同条件下的收敛情况对比,LEACH-WGR-PSO在39轮后收敛,LEACH-WGR-SSA在34轮收敛。虽然收敛次数接近,但LEACH-WGR-SSA算法寻优的最佳适应度值优于LEACH-WGR-PSO。因此,LEACH-WGR-SSA在此场景下具有一定的优势。

|
Download:
|
| 图 3 收敛情况对比 Fig. 3 Comparison of iterative convergence among algorithms | |
本文针对输变电场景传感器众多,并且没有组网能力的特点,提出采用计算能力高的中继节点收集传感器信息,并对中继节点进行组网的解决方案,并根据这一方案,研究中继节点间的组网,提出一种轮换无线网关节点的路由分簇算法,同时加入麻雀搜索的智能优化算法,优化簇首的选举。对于无线网关节点的选举考虑到了节点剩余能量、距离质心的位置和邻接节点个数;对于中继节点的选举同样考虑了节点剩余能量和邻接节点个数,也考虑到无线网关节点的距离。同时加入Levy飞行策略对SSA算法中发现者位置更新进行优化,防止算法陷入局部最优。仿真结果表明,该算法延长了网络的生存周期,均衡了能耗,同时改进后的麻雀搜索算法寻优能力在该场景下有一定的优势。
虽然LEACH-WGR-SSA算法在仿真中取得了较好的结果,但并未考虑到传感器到中继节点的接入,传感器接入的个数和传输的数据量对整个网络的能耗有一定的影响。后续的研究将考虑这一因素,对算法和模型进行改进,运用到真实的场景中。
| [1] |
马祖长, 孙怡宁, 梅涛. 无线传感器网络综述[J]. 通信学报, 2004, 25(4): 114-124. |
| [2] |
Yan J J, Zhou M C, Ding Z J. Recent advances in energy-efficient routing protocols for wireless sensor networks: a review[J]. IEEE Access, 2016, 4: 5673-5686. Doi:10.1109/ACCESS.2016.2598719 |
| [3] |
Heinzelman W R, Chandrakasan A, Balakrishnan H. Energy-efficient communication protocol for wireless microsensor networks[C]//Proceedings of the 33rd Annual Hawaii International Conference on System Sciences. Maui, HI, USA: IEEE, 2000: 1-10. DOI: 10.1109/HICSS.2000.926982.
|
| [4] |
Heinzelman W B, Chandrakasan A P, Balakrishnan H. An application-specific protocol architecture for wireless microsensor networks[J]. IEEE Transactions on Wireless Communications, 2002, 1(4): 660-670. Doi:10.1109/TWC.2002.804190 |
| [5] |
黄利晓, 王晖, 袁利永, 等. 基于能量均衡高效WSN的LEACH协议改进算法[J]. 通信学报, 2017, 38(S2): 164-169. Doi:10.11959/j.issn.1000-436x.2017270 |
| [6] |
Hu M, Wang Y X. Two-level linear clustering protocol based on wireless sensor networks[J]. Journal of Electronic Science and Technology, 2016, 14(3): 257-261. Doi:10.11989/JEST.1674-862x.505071 |
| [7] |
Lee J S, Kao T Y. An improved three-layer low-energy adaptive clustering hierarchy for wireless sensor networks[J]. IEEE Internet of Things Journal, 2016, 3(6): 951-958. Doi:10.1109/JIOT.2016.2530682 |
| [8] |
李安超, 陈桂芬. 能量异构无线传感器网络分簇路由改进算法[J]. 传感技术学报, 2017, 30(11): 1712-1718. Doi:10.3969/j.issn.1004-1699.2017.11.017 |
| [9] |
Gharaei N, Abu Bakar K, Mohd Hashim S Z, et al. Collaborative mobile sink sojourn time optimization scheme for cluster-based wireless sensor networks[J]. IEEE Sensors Journal, 2018, 18(16): 6669-6676. Doi:10.1109/JSEN.2018.2851300 |
| [10] |
Daneshvar S M M H, Alikhah Ahari Mohajer P, Mazinani S M. Energy-efficient routing in WSN: a centralized cluster-based approach via grey wolf optimizer[J]. IEEE Access, 2019, 7: 170019-170031. Doi:10.1109/ACCESS.2019.2955993 |
| [11] |
戴剑勇, 邓先红, 王彬, 等. 基于改进萤火虫优化神经网络的WSNs分簇路由协议[J]. 北京邮电大学学报, 2020, 43(3): 131-137. Doi:10.13190/j.jbupt.2019-161 |
| [12] |
Singh A, Rathkanthiwar S, Kakde S. LEACH based-energy efficient routing protocol for wireless sensor networks[C]//2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT): Chennai, India: IEEE, 2016: 4654-4658. DOI: 10.1109/ICEEOT.2016.7755602.
|
| [13] |
武小年, 张楚芸, 张润莲, 等. WSN中基于改进粒子群优化算法的分簇路由协议[J]. 通信学报, 2019, 40(12): 114-123. Doi:10.11959/j.issn.1000-436x.2019246 |
| [14] |
Xue J K, Shen B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. Doi:10.1080/21642583.2019.1708830 |
| [15] |
吕鑫, 慕晓冬, 张钧. 基于改进麻雀搜索算法的多阈值图像分割[J]. 系统工程与电子技术, 2021, 43(2): 318-327. DOI: 10.j.issn.1001-506x.2021.02.05.
|
| [16] |
薛建凯. 一种新型的群智能优化技术的研究与应用: 麻雀搜索算法[D]. 上海: 东华大学, 2020.
|
| [17] |
Lv Y, Tian Y. Design and application of sink node for wireless sensor network[C]//2010 2nd International Conference on Industrial and Information Systems: Dalian, China: IEEE, 2010: 487-490. DOI: 10.1109/INDUSIS.2010.5565803.
|
| [18] |
凡志刚, 郭文生, 桑楠. 一种基于蜂窝网格的传感器节点部署算法[J]. 传感器与微系统, 2008, 27(4): 15-17. Doi:10.13873/j.1000-97872008.04.021 |
| [19] |
Haklı H, Uğuz H. A novel particle swarm optimization algorithm with Levy flight[J]. Applied Soft Computing, 2014, 23: 333-345. Doi:10.1016/j.asoc.2014.06.034 |
| [20] |
王金伟, 孙华志, 孙德兵. 基于能耗的无线传感器网络最优簇首数研究[J]. 传感器与微系统, 2011, 30(7): 45-47, 50. Doi:10.13873/j.1000-97872011.07.023 |
| [21] |
梁青, 李卓冉, 韩昊澎, 等. 基于最优簇首数划分单元格的改进GAF算法[J]. 计算机应用研究, 2013, 30(12): 3622-3624. Doi:10.3969/j.issn.1001-3695.2013.12.027 |
 2023, Vol. 40
2023, Vol. 40 


