2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
改革开放以来,中国制造业规模高速增长,成为世界制造业第一大国,但同时也伴随着巨大规模的能源资源消耗。而过度的能源消费和对能源资源的过度依赖,将对生态环境产生威胁,对产业发展产生约束。节约资源是中国国情基础中的基础[1],节能减排、提高能源效率是中国社会经济可持续发展的重要目标之一。区域能源效率与产业结构状况和产业技术水平密切相关[2-3],而制造业作为区域经济发展的支柱和能源消费的主体,要加强结构优化、提高能源效率以达到高质量发展。正确认识区域制造业能源效率格局和产业结构的相互作用关系,对于区域节能减排、制造业健康可持续发展具有重要意义。
产业结构调整对能源效率提升的贡献已被诸多研究证实。有研究证实,经济结构的优化,可以促进整体经济系统生产效率和能源效率的提升[4-5]。如在部分时段,第一产业向第二产业、第二产业向第三产业、传统工业向高新技术工业调整被证实有利于提升能源效率[6-8]。另外,工业结构由重工业主导向轻工业主导调整,也会降低经济系统的能源强度[9]。学者们则进一步考虑空间因素,从区域格局层面研究了能源效率与产业发展的分布及相关关系,并提出具有区域针对性的调整对策[10-13]。Liu等[14]的研究表明,中国产业集聚对能源效率的提升有显著的促进作用,但这种促进作用的程度具有区域差异性;产业转移和经济发展可以促进区域能源效率差异减小,产业转移的规模会对承接地的能源强度产生倒U型影响[15-17]。产业结构和能源效率的关系研究多以产业结构高级度、合理度、集中度和工业化水平表示产业结构状况,采用耦合度模型[18-19]和回归模型[20-21]研究其与能源效率的相互作用关系,认为制定差异化的能源和产业结构优化政策是实现节能减排和经济发展双赢的前提[22]。
学者们从多角度、采用多种方法对能源效率和产业结构的关系进行了大量研究,对于促进产业和能源效率协调发展具有重要意义。而已有研究多以区域整体经济体系或某行业的能源效率为研究对象,将地区与制造业结合进行细化研究的文献较少;产业结构多由3大产业的比重及其数学组合来表征,仅能宏观反映其工业化程度,无法对其产业结构内涵进行深入分析。江苏省是中国经济最发达的东部省份之一,同时也是制造业大省,2016年,江苏省制造业产值占中国总产值的12.29 %,相应地,能源消耗占9.67 %。然而,2016年江苏省有近95 % 的能源使用来自其他省份[23],具有制造业规模庞大与能源短缺并存的特点,在制造业能源效率与结构转型的研究中具有较强的典型意义。基于此,本研究将区域制造业能源效率与细分行业结构综合起来,依托数据包络分析法(data envelopment analysis, DEA)、能源效率指数和高级度指数对江苏省制造业能源效率与结构高级度的时间特征进行分析,在此基础上探讨二者的耦合关系及空间格局,划分制造业能源效率与结构高级度的耦合类型区,并对不同耦合类型区进行产业结构解构,以期为江苏省制定能源发展规划、产业结构调整政策提供科学决策依据。
1 研究方法与数据处理 1.1 数据来源与数据处理本文数据来源于2007和2017年的《中国工业统计年鉴》、《江苏省统计年鉴》、《中国城市统计年鉴》与江苏省13个地级市的统计年鉴。原始数据包括能源效率指数测算中的制造业增加值、制造业固定资产投资额、制造业企业年平均就业人数、制造业能源消费总量以及高级度指数测算中的制造业总产值,均采用规模以上制造业企业数据。
对于能源综合技术效率投入产出指标的选取。在充分考虑制造业经济产出的投入要素组合的基础上,结合各研究成果对全要素能源效率投入产出指标的选择后,产出指标选取制造业增加值代表经济产出,投入指标选取制造业固定资产投资额、制造业企业年平均就业人数和制造业企业能源消费总量等分别代表资本、劳动力和能源投入。
对于制造业结构高级度指数的计算数据,根据各地级市高技术、中技术、低技术3类产业总产值占制造业总产值比重计算得到。耦合度的计算数据,由各地区能源效率指数值与高级度指数值进行min-max标准化处理得到。应用Deap2.1、Excel和ArcMap10.5软件对数据进行计算和分析。
1.2 能源效率指数测算能源效率的测算可划分为单要素能源效率和全要素能源效率两大类,其中全要素能源效率考虑了多投入要素与产出要素之间的关系,可以更好地反映能源和经济之间的相互作用关系,目前已被学者们普遍采用。全要素能源效率的测算方法中,DEA无需预先估计参数和人为确定权重,也无需考虑投入产出间的函数关系,对社会经济系统的多投入和产出指标的相对效率评价很有效[24],目前已经得到广泛应用。因此本文采用DEA模型进行全要素能源效率测算。为突出能源消费在能源效率中的重要性,将DEA全要素能源综合技术效率与能源生产率(单位能源GDP)相乘作为能源效率指数指标,进一步分析能源效率与产业结构的耦合关系。
DEA是在“相对有效评价”概念基础上发展起来的一种系统分析方法,采用数学规划模型,构造非参数的包络生产前沿面评价多输入和多输出的决策单元(decision making unit, DMU)间的相对效率[25]。本文采用DEA模型中基于规模报酬可变的VRS模型来测算能源综合技术效率,模型如下:
| $ \left\{\begin{array}{c} \min \left(\theta-\varepsilon\left(e_1^T s^{-}+e_2^T s^{+}\right)\right), \\ \text {s. t. } \sum x_{m i} \lambda_m+s^{-}=\theta x_i^n ; i=1, \cdots, I, \\ \sum y_{m k} \lambda_m+s^{+}=y_i^m ; k=1, \cdots, K, \\ \lambda_m \geqslant 0 ; m=1, 2, \cdots, M . \end{array}\right. $ | (1) |
式中:M为研究单元个数,I和K分别为投入指标和产出指标个数;xmi表示第m个研究单元的第i种投入指标值,ymk表示第m个研究单元第k种产出指标值。θ(0 < θ≤1)为能源综合技术效率,当θ=1时,该研究单元能源效率在研究区中位于最优生产前沿面上。能源综合技术效率可分解为纯技术效率和规模效率的乘积,纯技术效率为假定生产达到最优规模时投入要素的生产效率,反映地区利用管理和技术使能源产出最大化的能力;规模效率则反映实际生产规模和最优规模的差距[26],规模效率越大,表明规模越接近最优规模。
能源生产率即单位能源消耗的经济产出,表示能源利用的宏观效率。制造业能源生产率的计算公式为
| $ E_{\mathrm{P}}=Y_i / X_i, $ | (2) |
式中:EP为能源生产率,单位为万元/t标准煤;Xi为i年度制造业能源消费总量,单位为t标准煤;Yi为i年度制造业增加值,单位为万元。
最后,能源效率指数E(x)为
| $ E(x)=\theta \times E_{\mathrm{P}}, $ | (3) |
式中:θ为能源综合技术效率,EP为能源生产率。
1.3 高级度指数测算经济合作与发展组织将制造业结构依据技术水平分为低技术、中低技术、中高技术和高技术4类[27];在构造产业结构高级度时,有学者将中高技术和高技术合并为高技术,将制造业分为低技术、中技术、高技术3类[28]。本文采用上述分类方法,从技术密集角度出发构建制造业结构高级度指数来表征制造业高级化程度,具体分类如表 1所示。
|
|
表 1 基于技术密集程度的制造业产业分类 Table 1 Classification of manufacturing industries according to technology intensity |
对于制造业结构高级度指数的计算模型,主要参考李建新等[28],采用夹角余弦法对制造业结构高级度进行测算。具体算法如下:首先,将各类产业产值占制造业总产值的比重作为空间向量的1个分量,构成三维向量X0=(X1, 0, X2, 0, X3, 0);然后,分别计算X0与产业由低层次到高层次排列的向量X1=(1, 0, 0),X2=(0, 1, 0),X3=(0, 0, 1)的夹角θ1,θ2,θ3:
| $ \theta_j=\arccos \frac{\sum_{i=1}^3\left(x_{i, j} \times x_{i, 0}\right)}{\sum_{i=1}^3\left(x_{i, j}^2\right)^{1 / 2} \times \sum_{i, 0}^3\left(x_{i, 0}^2\right)^{1 / 2}}, $ | (4) |
然后累积相加得到制造业结构高级度指数
| $ P(x)=\sum_{k=1}^3 \sum_{i=1}^k \theta_i, $ | (5) |
式中:P(x)为制造业结构高级度指数,P(x)大表示产业结构高级化水平越高。
1.4 耦合度模型耦合度反映2个及2个以上系统之间相互影响和相互作用的程度。制造业发展对能源消费产生影响,同时能源资源对制造业产业结构产生约束作用。对于耦合度模型的构建,主要参考文献[29],选取以变异系数为基础的耦合评价模型来评价制造业能源效率与制造业产业结构间的耦合关系。耦合度模型为
| $ C=\left\{\left[P(x)^{\prime} E(x)^{\prime}\right] /\left[\frac{P(x)^{\prime}+E(x)^{\prime}}{2}\right]^2\right\}^k, $ | (6) |
式中:C为耦合度; P(x)′和E(x)′为采用极值法标准化处理后的产业高级度指数值和能源效率指数值; k代表区别系数,取值为2~5,为加强区分度,将k取为4[18]。
耦合度模型可以反映制造业能源效率和产业结构的耦合程度,但当能源效率和产业结构高级化水平都很低时,测算出的耦合度却很高,这显然无法有效体现能源效率与产业结构的耦合关系。因此构建可以反映系统水平的耦合协调度模型,将耦合度和耦合协调度结合起来,从而反映制造业能源效率与产业结构的真实协调发展水平。模型为
| $ D=\sqrt{C \times T}, $ | (7) |
式中:D为耦合协调度;T=αP(x)′+βE(x)′, 为制造业能源效率系统与产业结构系统综合协调指数。α、β为待定系数,反映制造业能源效率和制造业产业结构的贡献系数。由于产业结构变化会影响能源效率水平,但产业结构不是影响能源效率的唯一驱动因素,因此将α和β分别赋值0.4和0.6,C和D的值均位于0~1。
2 制造业能源效率与结构高级度测算结果分析 2.1 制造业能源效率指数及其分解评价 2.1.1 能源综合技术效率评价从能源综合技术效率(图 1(a),1(d))来看,2006年,能源综合技术效率整体上呈现东部大于西部、南部大于北部的空间特征。能源综合技术效率达到最优的城市有3个,包括苏州、无锡和南通,最低值为南京。至2016年,能源综合技术效率均值有所提升(表 2),南部高于北部的格局更加显著。从地区间差异来看,2006年综合技术效率最低值为0.325(南京),而2016年最低值为0.575(淮安),说明江苏省地级市间能源综合技术效率的差距有所缩小。综合技术效率达到最优的城市增长至6个,包括南京、无锡、苏州、南通、盐城和宿迁。值得注意的是,2016年南京的产出变量和3个投入变量分别为2006年的3.7倍和1.6倍、1.3倍、0.5倍,产出增长远远大于投入增长,以致其综合技术效率由最低转变为最优。
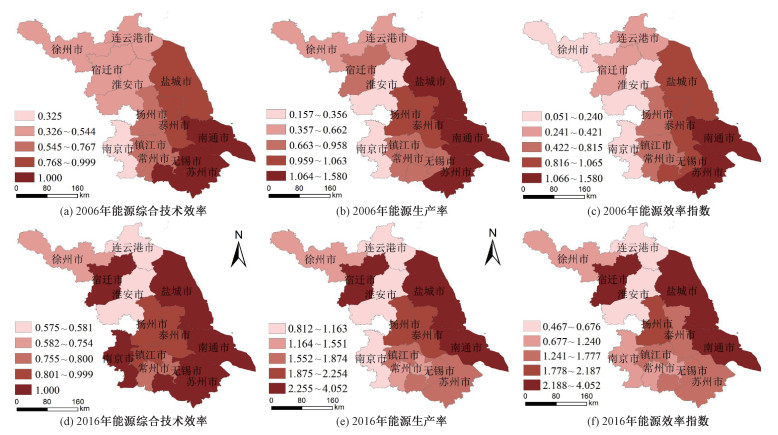
|
Download:
|
| 图 1 江苏省各地级市能源效率分布图 Fig. 1 Distribution map of energy efficiency in prefecture level cities in Jiangsu Province | |
|
|
表 2 江苏省能源综合技术效率 Table 2 DEA energy technology efficiency in Jiangsu Province |
从对能源综合技术效率的贡献来看,纯技术效率均值明显高于规模效率(表 2)。典型城市如宿迁,其在2006年为纯技术效率有效而规模效率无效,且处于规模效率递增的状态,2016年其制造业GDP增长11倍,达到规模最优,从而达到综合技术效率有效。这从侧面反映了在研究期内,纯技术效率的地区差距较小,地区间制造业发展的规模差距大于技术和管理水平的差距。
2.1.2 能源生产率评价能源生产率可以直接反映能源利用的经济效益。从图 1(b)、1(e)可以看出,2006—2016年,江苏省能源生产率提升显著,其均值由0.89万元/t标准煤提升至1.96万元/t标准煤。空间上看,两个时点能源生产率的分布格局高度相似。从2016年的整体情况来看,研究区能源生产率分布极不均衡,最高值达最低值的4.99倍。能源生产率的高值地区包括沿海的南通、盐城,以及北部的宿迁,其中宿迁的工业结构中轻工业产值比重较大(轻工业产值占52.3 %),是江苏唯一轻工业比重大于重工业的地区,导致其能耗很低,能源效率相对较高;中值地区主要集中在沿江的扬州、镇江、苏州、泰州、无锡,均为重工业占比较高、能源消耗量大的城市,能源生产率相对较低;低能源生产率地区包括南京、常州、徐州、连云港和淮安,这些地区大体可以分为2类:第1类为以重工业为主且制造业规模较大的镇江、南京、常州和徐州(重工业占制造业总产值的比例分别为82.0 %、76.8 %、76.6 % 和66.0 %);第2类为重工业比重不高但制造业规模相对较小,能源效率可能受其技术水平和规模效益限制的淮安和连云港。
2.1.3 能源效率指数评价本文的能源效率指数为能源综合技术效率与能源生产率的乘积,是结合技术因素和能耗强度的综合能效评价。由图 1(c)、1(f)可以看出,2006—2016年,各地级市能源效率指数显著提升,其空间分布在趋势上更接近于能源生产率的空间分布,说明能源效率指数的测算中能源生产率的贡献较大。从2016年的情况看,能源效率指数空间上呈由东向西逐步减弱、南部地区略微高于西部地区的态势。宿迁、盐城、南通的能源生产率及能源综合技术效率均处于高值水平,表明其制造业的技术管理水平和能源高效利用水平均处在江苏省前列。南京、苏州和无锡均为能源综合技术效率最优而能源生产率低值地区,说明其综合考虑多要素投入的能源综合效率优于仅考虑能源消费单投入要素的能源生产率。而连云港、淮安和徐州两方面均处于低值,说明其制造业能源效率在省内处于极低水平,是未来能源效率提升的关键区域。
2.2 制造业结构高级度评价制造业结构高级化是指制造业从低水平向高水平发展的动态过程,是制造业结构重心由低技术向中技术和高技术转移的过程。由表 3和图 2可以看出,2006—2016年,各地级市的制造业高级度指数均有不同程度的提高,其空间分布格局基本一致。从差异变化看,地级市间高级度指数的变异系数从0.093降低至0.085,说明至2016年地级市间高级度指数的差异有所减小。高级度指数增幅最大的为南通,增长了0.956,增幅较大的还包括镇江、盐城、徐州和常州,其中,南通由于过江通道建设等带来交通区位的巨大改善,吸引通信设备、计算机等高技术制造业的集聚使得其高级度指数大幅提升。可以发现,增长幅度较大的地区主要集中在高级度指数基数在平均值以下,且具有良好产业基础的城市,其他城市提升幅度较小。因此,地级市间差异缩小主要是由于中、低值区域的快速增长。
|
|
表 3 江苏省制造业高级度 Table 3 Manufacturing structure up-grade index in Jiangsu Province |
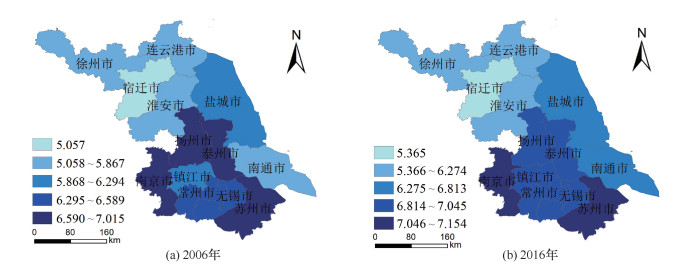
|
Download:
|
| 图 2 江苏省制造业结构高级度空间分布 Fig. 2 Spatial distribution of manufacturing structure up-grade index in Jiangsu Province | |
从2016年高级度指数的空间分布来看(图 2(b)),南京—苏州两极格局显著。高级度指数高值区主要分布在南京和苏州,它们具有优越的区位条件、雄厚的制造业基础及科技实力,是经济发展的重点节点城市,其制造业高级度位于全省前列。中值区主要集中于沿江的扬州、泰州、镇江、常州和无锡一带,它们在空间上相邻,具有相似的自然资源条件、产业环境及投资环境,其制造业结构高级度十分相似。低值区分布在南通、盐城、淮安、宿迁、连云港和徐州,均位于长江以北;其中,南通的制造业高级度虽有大幅提升,但仍位于省内较低水平;宿迁、淮安、徐州和连云港的高级度指数远低于江苏省平均水平,其中宿迁和淮安的低技术产业产值占比均较高(2016年分别为56 %、39 %),制造业发展的产业基础较差,导致其产业结构高级度指数极低;徐州具有较大的制造业规模,但产业重心集中在化工、农副食品加工等资源密集型和劳动密集型产业,高技术制造业较少,导致其高级度指数偏低。
3 江苏省制造业能源效率与结构高级度空间耦合特征分析 3.1 耦合度及耦合空间分布针对江苏省各地级市制造业能源效率与结构高级度耦合度评价,采用2016年13个城市制造业高级度指数和能源效率指数的标准化值进行截面耦合分析,得到耦合情况如图 3所示。2016年,江苏省地级单元能源效率与制造业结构高级度耦合度的空间分布极不均衡,耦合度值从0.001至0.994不等,耦合协调度值由0.001至0.841不等。全省耦合度均值为0.383,整体处于低水平耦合,说明现阶段研究区制造业产业结构高级度与能源效率的相互关系不显著。高度耦合的地区包括南通和盐城,其产业结构高级度与能源效率相互影响,较为协调;耦合度较高的为扬州、徐州、泰州、镇江、无锡和苏州,其中,徐州为低水平的耦合,其他沿江5市为较高水平的耦合;低耦合度地区包括常州、南京、连云港、宿迁和淮安。

|
Download:
|
| 图 3 江苏省制造业能源效率与结构高级度的耦合分布 Fig. 3 Coupling distribution of energy efficiency and structure up-grade index of manufacturing industry in Jiangsu Province | |
为划分不同地级市能源效率与制造业高级度的耦合类型,将能源效率指数E(x)和产业结构高级度指数P(x)经过标准化方法无量纲化得到可对比值E和P,E和P都是均值为0、方差为1的样本数值。通过对比E和P,将制造业能源效率与产业结构高级度的耦合关系分为4种类型区(图 4):1)高能源效率-高制造业高级度区域(E和P均大于0.6),说明制造业能源效率与产业结构高级化同步发展且均为高水平,2016年江苏省各地级市中无此类区域;2)低能源效率-低制造业高级度区域(E和P均小于-0.6),主要分布在连云港、淮安和徐州;3)能源效率滞后型区域(E < P,且E、P不满足1)和2)),主要分布在除南通外的沿江区域,包括南京、苏州、常州、泰州、镇江、无锡和扬州,该区域能源效率滞后于制造业结构高级化水平;4)制造业高级度滞后型区域(P < E,且E、P不满足1)和2)),主要分布在南通、盐城和宿迁。
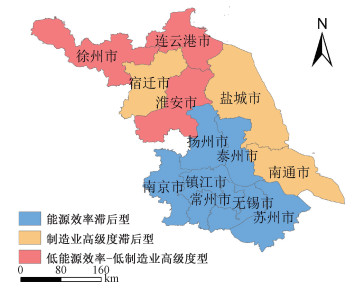
|
Download:
|
| 图 4 江苏省制造业能源效率和结构高级度耦合类型分区 Fig. 4 Distribution of coupling types of manufacturing structure up-grade index and energy efficiency in Jiangsu Province | |
通过计算江苏省各个制造业部门的能源消耗强度,取能源强度大于0.350 t标准煤/万元的前6位制造业部门为高能耗部门,分别为黑色金属冶炼和压延加工业、石油加工、炼焦和核燃料加工业、其他制造业、化学原料和化学制品业、非金属矿物制品业和黑色金属冶炼和压延加工业。计算各类型区不同制造业部门产值比例和高能耗部门产值比例(表 4)可发现以下特征;
|
|
表 4 不同类型耦合区域制造业结构特征 Table 4 Structural characteristics of manufacturing in different types of coupling regions |
1) 能源效率滞后型区域的主导产业以计算机、通信和其他电子设备制造业、电气机械和器材制造业、通用设备制造业、汽车制造业等高技术产业和化学原料和化学制品制造业、黑色金属冶炼和压延加工业等高能耗产业为主,形成以高技术产业和高能耗产业共同主导制造业发展的模式。其高能耗部门结构比重较大,占全部制造业产值的25.0 %,是制约其能源效率提升的主要原因之一。另外,这类地区具有优越的区位条件和雄厚的工业基础,为江苏省制造业布局最密集、规模最大的区域,但目前其制造业规模及结构高级化对能源效率提升的作用有限。该类地区作为能源资源开发与消费的重要区域,应积极发展高新技术产业,在产业向高技术高附加值转型的同时,注重资源能源的节约集约利用。既要从供给侧结构性改革的角度消除过剩、落后产能的高能耗部门,也应充分利用以南京为主的科技实力优势,提升能源基础原材料的质量和效能,积极研发和培育新能源和绿色产业[30]。
2) 制造业高级度滞后型区域,其主导产业以装备制造等高技术制造业,化工等高能耗制造业以及纺织、食品加工等轻工业为主。其高能耗部门比重在3类地区中最低,为20.3 %。高能耗部门以及高技术部门比重均相对较低是制造业结构高级度滞后于能源效率的主要原因。南通和盐城处于工业快速发展阶段,应充分利用其沿海滩涂资源优势,积极发展风能、生物质能等可再生能源,优化能源结构[31],承接部分高技术嫁接的资源密集型产业转移,同时调整制造业结构向技术密集型主导发展,实现制造业结构高级化和能源效率的良性互动和协调发展。与南通和盐城不同,宿迁的主导产业以木材加工、食品饮料、纺织服装等轻工业和机电装备制造为主,且宿迁市轻工业已形成一定的规模经济,具有一定的产业效率,因此其能源效率处于江苏省较高水平。但从长期来看,当前宿迁的制造业结构以要素驱动型产业为主,经济效益有限,无法引领长期的经济发展,应积极提升原有轻工业的科技含量并发展相应的生产性服务业,注重发展创新型产业,在承接发达城市产业转移时防止高能耗高污染产业转移,注重高新技术产业的引进,提升经济效益和资源能源利用效率。
3) 低能源效率-低制造业高级度型区域,该类地区的主导产业以化工、冶金等高能耗资源密集型产业,食品、木材等劳动力密集型产业和电子、机械器材等装备制造业为主。其高能耗部门比重在3类地区中最高,为29.9 %,高能耗产业比重和低高技术产业比重的制造业结构严重制约了其能源效率的提升。目前这类地区工业发展处于高度重工业化阶段,能源开发与消费的规模不断提高,但由于经济实力和科技实力在省内相对较弱,在科技投入和能源资源节约集约利用投入方面不足,导致其制造业能源效率位于江苏省最低水平。该类地区为江苏省未来加强集约节约利用资源、提高资源利用效率的重要区域。该类地区应依托地方优势资源,积极发展技术密集型产业,承接中心城市和国外产业转移,注重提升生产效率和能源效率。对于制造业规模较小的连云港和淮安,还应加快产业集聚,形成规模效益以提升生产效率。
4 结论与讨论1) 从制造业能源效率指数及其分解情况来看,2006—2016年江苏省能源效率指数均值提升了1.5倍,各地级市制造业能源效率均显著提高。基于全要素投入的能源综合技术效率和基于能源消费的能源生产率具有不同的空间结构特征。江苏北部的连云港、淮安和徐州、以及苏南的南京、镇江和常州等重工业城市是未来能源效率提高的关键区域。
2) 从制造业结构高级度来看,各地级市的制造业高级度指数均有不同程度地提高,且空间差异有所缩小。空间上,以南京—苏州为高值区的两极格局显著,南部地区整体上高于北部地区,中值区集中于无锡、常州、镇江、泰州和扬州沿江一带,低值区分布在江苏沿海一带和北部的徐州、宿迁和淮安。苏北5市的产业结构高级度指数值均在江苏省均值水平以下,就产业结构高级度来看,仍存在较强的南北空间差异。
3) 从制造业能源效率与制造业结构的耦合度来看,江苏省整体耦合情况不佳,处于初级协调水平。根据制造业能源效率和结构高级度的耦合关系,将各地级市划分为能源效率滞后型区域、制造业高级度滞后型区域和低能源效率-低制造业高级度区域,通过对不同类型区的产业结构解构,发现低能源效率-低制造业高级度区域低附加值、高能耗制造业部门占较大比重,为江苏省未来产业结构优化、提高能源资源效率的关键区域。
江苏省制造业能源效率与产业发展不均衡不耦合的现状,说明当前阶段制造业结构高级化对能源效率提升的促进作用有限。其形成原因主要有以下方面:首先,江苏省制造业专业化分工的空间差异,沿江发达地区产业结构以资源密集型和技术密集型产业共同主导,沿海地区以劳动密集型产业和技术密集型产业主导,苏北欠发达地区以资源密集型产业和劳动密集型产业主导,故出现沿江地区能源效率滞后而沿海地区制造业高级度滞后的格局;另外,区域内几大经济区(南京都市圈、苏锡常、沿海地区和徐州都市圈)未形成合理分工,苏北地区的基础设施和政策环境还有待完善;北部地区缺少能够辐射周边城市的中心城市,且徐州都市圈不属于长三角城市群,与南部地区联系较弱。
本研究从制造业产业结构优化和能源利用效率关系的角度出发,分析江苏省产业发展与能源效率的空间耦合关系。与传统的针对全社会能源效率与3大产业结构的空间关系研究相比,采用制造业部门数据为进行更小的地理尺度分析提供可能,有助于理解省级尺度制造业结构与能源消耗的交互作用关系,这对推进集约利用能源、促进制造业结构转型具有一定的政策借鉴意义。但制造业结构和能源效率的内涵远比当前测算方法所表征的更丰富,二者之间的内部交互作用也更加复杂,还须辅之以技术投入、集中度、区位熵等产业结构指标,以及碳排放、环境污染等生态环境指标的进一步分析。
| [1] |
陆大道. 关于"十四五"规划: 领域与认识[J]. 地理科学, 2020, 40(1): 1-5. |
| [2] |
周勇, 李廉水. 中国能源强度变化的结构与效率因素贡献: 基于AWD的实证分析[J]. 产业经济研究, 2006(4): 68-74. Doi:10.3969/j.issn.1671-9301.2006.04.009 |
| [3] |
Huang J B, Chen X. Domestic R&D activities, technology absorption ability, and energy intensity in China[J]. Energy Policy, 2020, 138: 111184. Doi:10.1016/j.enpol.2019.111184 |
| [4] |
Mi Z F, Wei Y M, Wang B, et al. Socioeconomic impact assessment of China's CO2 emissions peak prior to 2030[J]. Journal of Cleaner Production, 2017, 142: 2227-2236. DOI: 10.j.jclepro.2016.11.055.
|
| [5] |
周彦楠, 杨宇, 程博, 等. 基于脱钩指数和LMDI的中国经济增长与碳排放耦合关系的区域差异[J]. 中国科学院大学学报, 2020, 37(3): 295-307. Doi:10.7523/j.issn.2095-6134.2020.03.002 |
| [6] |
Wurlod J D, Noailly J. The impact of green innovation on energy intensity: an empirical analysis for 14 industrial sectors in OECD countries[J]. Energy Economics, 2018, 71: 47-61. Doi:10.1016/j.eneco.2017.12.012 |
| [7] |
何则, 杨宇, 宋周莺, 等. 中国能源消费与经济增长的相互演进态势及驱动因素[J]. 地理研究, 2018, 37(8): 1528-1540. |
| [8] |
Li K, Lin B Q. The nonlinear impacts of industrial structure on China's energy intensity[J]. Energy, 2014, 69: 258-265. Doi:10.1016/j.energy.2014.02.106 |
| [9] |
Su Y Q, Liu X, Ji J P, et al. Role of economic structural change in the peaking of China's CO2 emissions: an input-output optimization model[J]. Science of the Total Environment, 2021, 761: 143306. Doi:10.1016/j.scitotenv.2020.143306 |
| [10] |
宋涛, 董冠鹏, 唐志鹏, 等. 能源-环境-就业三重约束下的京津冀产业结构优化[J]. 地理研究, 2017, 36(11): 2184-2196. |
| [11] |
关伟, 许淑婷. 中国能源生态效率的空间格局与空间效应[J]. 地理学报, 2015, 70(6): 980-992. Doi:10.11821/dlxb201506011 |
| [12] |
刘佳骏, 董锁成, 李宇. 产业结构对区域能源效率贡献的空间分析: 以中国大陆31省(市、自治区)为例[J]. 自然资源学报, 2011, 26(12): 1999-2011. |
| [13] |
王强, 樊杰, 伍世代. 1990—2009年中国区域能源效率时空分异特征与成因[J]. 地理研究, 2014, 33(1): 43-56. |
| [14] |
Liu J, Cheng Z H, Zhang H M. Does industrial agglomeration promote the increase of energy efficiency in China?[J]. Journal of Cleaner Production, 2017, 164: 30-37. Doi:10.1016/j.clepro.2017.06.179 |
| [15] |
Zhao X G, Lu F. Spatial distribution characteristics and convergence of China's regional energy intensity: an industrial transfer perspective[J]. Journal of Cleaner Production, 2019, 233: 903-917. Doi:10.1016/j.clepro.2019.06.073 |
| [16] |
Li Y M, Sun L Y, Zhang H L, et al. Does industrial transfer within urban agglomerations promote dual control of total energy consumption and energy intensity?[J]. Journal of Cleaner Production, 2018, 204: 607-617. Doi:10.1016/j.elepro.2018.08.342 |
| [17] |
张琨. 产业转移对能源强度的影响[J]. 合作经济与科技, 2018(12): 42-43. Doi:10.13665/i.cnki.hzjjykj.2018.12.017 |
| [18] |
关伟, 许淑婷. 辽宁省能源效率与产业结构的空间特征及耦合关系[J]. 地理学报, 2014, 69(4): 520-530. Doi:10.11821/dlxb201404008 |
| [19] |
江洪, 赵宝福. 碳排放约束下能源效率与产业结构解构、空间分布及耦合分析[J]. 资源科学, 2015, 37(1): 152-162. |
| [20] |
吕明元, 陈维宣. 中国产业结构升级对能源效率的影响研究: 基于1978—2013年数据[J]. 资源科学, 2016, 38(7): 1350-1362. |
| [21] |
王兴民, 王强, 董洁芳. 基于灰色关联模型的能源消费与经济增长的关系: 以新疆为例[J]. 中国科学院大学学报, 2017, 34(5): 598-609. Doi:10.7523/j.issn.2095-6134.2017.05.010 |
| [22] |
唐晓华, 刘相锋. 能源强度与中国制造业产业结构优化实证[J]. 中国人口·资源与环境, 2016, 26(10): 78-85. Doi:10.3969/j.issn.1002-2104.2016.10.010 |
| [23] |
Jiang L, Zhou H F, He S X. Does energy efficiency increase at the expense of output performance: evidence from manufacturing firms in Jiangsu Province, China[J]. Energy, 2021, 220: 119704. Doi:10.1016/j.energy.2020.119704 |
| [24] |
赵媛, 郝丽莎, 杨足膺. 江苏省能源效率空间分异特征与成因分析[J]. 地理学报, 2010, 65(8): 919-928. Doi:10.11821/xb201008003 |
| [25] |
魏权龄. 数据包络分析(DEA)[J]. 科学通报, 2000, 45(17): 1793-1808. |
| [26] |
于婷婷, 左冰, 宋玉祥, 等. 中国旅游业发展对区域经济效率的影响: 基于中国283个地级市的实证证据[J]. 地理研究, 2020, 39(6): 1357-1369. Doi:10.11821/dlyj20190471 |
| [27] |
傅元海, 叶祥松, 王展祥. 制造业结构变迁与经济增长效率提高[J]. 经济研究, 2016, 51(8): 86-100. |
| [28] |
李建新, 杨永春, 蒋小荣, 等. 中国制造业产业结构高级度的时空格局与影响因素[J]. 地理研究, 2018, 37(8): 1558-1574. Doi:10.11821/dlyj201808007 |
| [29] |
马丽, 金凤君, 刘毅. 中国经济与环境污染耦合度格局及工业结构解析[J]. 地理学报, 2012, 67(10): 1299-1307. Doi:10.11821/xb201210001 |
| [30] |
马丽. 基于产业环境耦合类型的沿海地区产业绿色转型路径研究[J]. 地理研究, 2018, 37(8): 1587-1598. Doi:10.11821/dlyj201808009 |
| [31] |
边文越, 陈挺, 陈晓怡, 等. 世界主要发达国家能源政策研究与启示[J]. 中国科学院院刊, 2019, 34(4): 488-496. Doi:10.16418/j.issn.1000-3045.2019.04.014 |
 2023, Vol. 40
2023, Vol. 40 


