2. Key Laboratory of Big Data Mining and Knowledge Management, Chinese Academy of Sciences, Beijing 100049, China;
3. Beijing Tongren Eye Center, Beijing Tongren Hospital, Capital Medical University, Beijing 100730, China
2. 中国科学院大数据挖掘与知识管理重点实验室, 北京 100049;
3. 首都医科大学附属北京同仁医院眼科中心, 北京 100730
Suppose that X1, …, Xn∈
| $ {H_0}:{\boldsymbol{\mu }} = {{\boldsymbol{\mu }} _0} \;{\rm{vs.}}\; H_{1}:{\boldsymbol{\mu }} \ne {{\boldsymbol{\mu }} _0}. $ | (1) |
under n < p. This is the so-called " large p, small n" paradigm. When p is fixed and under the assumption of normal distribution, a traditional method to test (1) is Hotelling's test statistic. However, Hotelling's test is not defined in the case of p > n because of the singularity of the sample covariance matrix. It is a challenge to the traditional method in high dimensional situation.
The challenge of testing (1) in high dimensional situation has attracted many researchers. Ref.[1] constructed the test statistics which avoid the inverse of the sample covariance matrix. but the test statistics can only be applied to the case of p/n→c∈(0, 1), which means that the increasing rate of the sample dimension should be same as the sample size. Ref.[2] proposed a new test statistic without any direct relationship between p and n. In practice, different components may have different scales. Therefore, scalar-invariant is an important property to a test statistic. Ref.[3], Ref.[4] and Ref.[5]> constructed a test statistic with the property of scalar-invariant and under the assumption that p=o(n2). Ref.[6] proposed a scalar-invariant test that allows the dimension to be arbitrarily large. But their test is not location shift invariant. However, under heavy-tailed distributions, which frequently arise in genomics and quantitative finance, the asymptotic properties of the above test statistics are not established, a natural result is that these tests tend to have unsatisfactory [JP2]power. Under the assumption of elliptical distributions, Ref.[7] proposed a novel non-parametric test based on spatial-signs, which is more powerful than the test in Ref.[2] for heavy-tailed multivariate distributions and has similar power to the test in Ref.[2] for multivariate normal distribution. But their test is not scalar-invariant. Ref.[8] proposed a novel scalar-invariant test based on multivariate-sign, which is more powerful than the test in Ref.[5] for heavy-tailed multivariate distributions. And their method is under the assumption that log(p)=o(n).
We propose a novel test for hypothesis (1) based on signed-rank method and our study have two main contributions. Firstly, the proposed test statistic works for more distributions because signed-rank method only requires that the distribution of the samples is symmetric. And the test statistic is available when p is arbitrarily large. Secondly, we show that, under null hypothesis, the proposed test statistic is asymptotically normal. Moreover, the simulation study shows that our method is scalar-invariant and robust, and is more efficient without the assumption of elliptical distributions.
1 A signed-rank-based high dimen-sional test 1.1 The proposed test statisticSuppose that Xi, i=1, …, n are independent and identically distribution random samples with dimension p. We denote that X(k)=(X1k, …, Xnk), k=1, …, p as the sample of the k-th dimension. And, let (r1k, …, rnk) be the rank of (|X1k|, …, |Xnk|). To test hypothesis (1), we proposed a test statistic based on signed-rank functions, which are defined as:
Ui=diag{sign(Xi1), …, sign(Xip)}(ri1, …, rip)T, where i=1, 2, …, n. Then, we consider the following U-statistic:
| $ {T_n} = \frac{{\sum _{i \ne j}^nU_i^{\rm{T}}{U_j}}}{{2n(n - {\rm{ }}1)}}. $ | (2) |
Set si=(si1, …, sip)T with covariance matrix Σs>0, where sij=sign(Xij). To establish the asymptotic properties of the U statistic under the null hypothesis, we need following conditions:
A1. P(sij=1)=P(sij=-1)=
A2. tr( Σs4)=o(tr2( Σs2)).
Remark 1.1 Condition A1 is necessary condition of the signed-rank test under null hypothesis and it indicates that the random samples have symmetric distributions. Under the first term in condition A1, we have E(sij)=0. Under the second term in condition A1, rij≠rkj for any i≠k and each j so that (r1j, …, rnj) is a permutation of all the elements in {1, …, n}. Condition A2 is similar to that applied in Ref.[2], and it is a quite mild condition on the eigenvalues of Σs.
Under H0, and then suppose condition A1 hold, it is easy to show that
| $ E({T_n}) = 0, $ |
and
| $ Var({T_n}) = \frac{1}{{2n(n{\rm{ }} - 1)}}{\rm{tr}}({\boldsymbol{\varSigma }} _u^2), $ |
where Σu=E(U1U1T).
Theorem 1.1 in the following establishes the asymptotic normality of Tn.
Theorem 1.1 Under H0, and then suppose conditions A1 and A2 hold, as n→∞ and p→∞,
| $ \frac{T_n}{\sqrt{2 n(n-1) {\rm{tr}}\left(\boldsymbol{\varSigma}_u^2\right)}} \stackrel{d}{\rightarrow} N(0, 1). $ | (3) |
Theorem 1.1 implies that we can reject H0 if Tn>zα(2n(n-1)tr(Σu2))1/2, where zα is the upper α-quantile of N(0, 1). The proof of Theorem 1.1 is conventional, so we omit the details. If someone needs detailed proof, please contact us.
1.2 Computational issueIn practice, in oder to estimate Var(Tn), the estimator for tr(Σu2) is needed. Similar to the estimator used by Ref.[2], we propose the following estimator:
where
When n and p are large, the computation of
Where
We comparr the performance of the proposed test (SR) with five alternatives: Ref.[1] (BS), Ref.[2] (CQ), Ref.[5] (SKK), Ref.[7] (WPL), Ref.[8] (FZW). All the following simulations are replicated 1 000 times. And, we set n=20, 50 and p=200, 1 000.
Example 1 We generate Xi from p-variate normal distribution N(μ, Σ). Two different choices of Σ are considered as follows: 1) Σ1=R; 2) Σ2=D1/2RD1/2. Where R=(σjk) with σjk=0.5|j-k| for 1≤j, k≤p, and D=diag{d1, …, dp} with dj=1I{1≤j≤p/4}+2I{p/4+1≤j≤p/2}+3I{p/2+1≤j≤3p/4}+4I{3p/4+1≤j≤p} for 1≤j≤p. Without loss of generality, we set μj=η for j=1, …, p, and
Table 1 stands for the performance of the six tests in Example 1. We can see that the power of SR is similar to those of BS, CQ and WPL when Σ=Σ1, and is more than those of BS, CQ and WPL when Σ=Σ2. It indicates that SR has better performance when the scales of different components are different. For example, when (n, p)=(20, 200), Σ=Σ2 and c=0.1, the power of SR, BS, CQ, and WPL are 0.547, 0.407, 0.420, and 0.394, respectively. And we observe that SR has better performance in power than SKK and FZW when p ≫ n. The reason is that SKK and FZW are under the assumptions that p cannot be much larger than n. For example, when (n, p)=(20, 1 000), Σ=Σ1 and c=0.15, the power of SR, SKK and FZW are 0.589, 0.413 and 0.347 respectively.
|
|
Table 1 The empirical size and power at the significance level of 5 % in Example 1 |
Example 2 In this example, Xi is generated from p-variate t-distribution with 3 degrees of freedom. The setting of mean vector μ and covariance Σ are the same as those in Example 1. And we select c=0.1 and 0.15 for μ to calculate the power.
Table 2 shows the simulation results in Example 2. We can see that SR have better performance in power than that of other five tests in all settings. For example, when (n, p)=(50, 200), Σ=Σ1 and c=0.15, the power of SR is 0.773 and the power of the other tests in this setting are 0.419, 0.538, 0.549, 0.577, and 0.610 respectively. For t-distribution is a common heavy-tailed distribution, the results in this table indicate that SR is robust. Table 3 shows the performance of the six tests in Example 3. It shows that SR are more powerful than other five tests in all settings. For example, when (n, p)=(20, 1 000), Σ=Σ2, and c=0.15, the power of BS, CQ, SKK, WPL, FZW, and SR are 0.626, 0.615, 0.695, 0.653, 0.650, and 0.949, respectively. Laplace distribution is not a elliptical distribution, and Table 3 shows that SR is more effective in this situation.
|
|
Table 2 The empirical size and power at the significance level of 5 % in Example 2 |
|
|
Table 3 The empirical size and power at the significance level of 5 % in Example 3 |
Example 3 In this example, Xi is generated from p-variate Laplace distribution. And we consider the same setting of mean vector μ and covariance Σ as those in Example 1. To calculate the power, we select c=0.1 and c=0.15 when n=20, and c=0.05 and c=0.075 when n=50.
Table 3 shows the performance of the six tests in Example 3. It shows that SR are more powerful than other five tests in all settings. For example, when (n, p)=(20, 1 000), Σ=Σ2, and c=0.15, the power of BS, CQ, SKK, WPL, FZW, and SR are 0.626, 0.615, 0.695, 0.653, 0.650, and 0.949, respectively. Laplace distribution is not a elliptical distribution, and Table 3 shows that SR is more effective in this situation.
Example 4 In this example, we generate Xi from a mixed distribution. Firstly, we generate Zij from normal distribution for 1≤j≤2p/5, generate Zij from t distribution with 3 degrees of freedom for 2p/5+1≤j≤7p/10, and generate Zij from Laplace distribution for 7p/10+1≤j≤p, and all Zij have mean 0 and variance 1. Then we let Xi=ΓZi+μ, where Γ is a p×p matrix with ΓΓT=Σ, and Zi={Zi1, …, Zip}T. And we consider the same setting of mean vector μ and covariance Σ as those in Example 1. To calculate the power, we select c=0.1 and c=0.15 when n=20, and c=0.05 and c=0.075 when n=50
Table 4 stands for the simulation results in Example 4. We can see that the power of SR is more than those of the other five tests in all settings. For example, when (n, p)=(50, 1 000), Σ=Σ2 and c=0.075, the power of SR is 0.757 and the power of the other tests in this setting are 0.214, 0.271, 0.548, 0.299 and 0.613 respectively. In practice, the variates usually have different distributions. Hence, the results in Table 4 indicate that SR is supposed to have better performancein application.
|
|
Table 4 The empirical size and power at the significance level of 5 % in Example 4 |
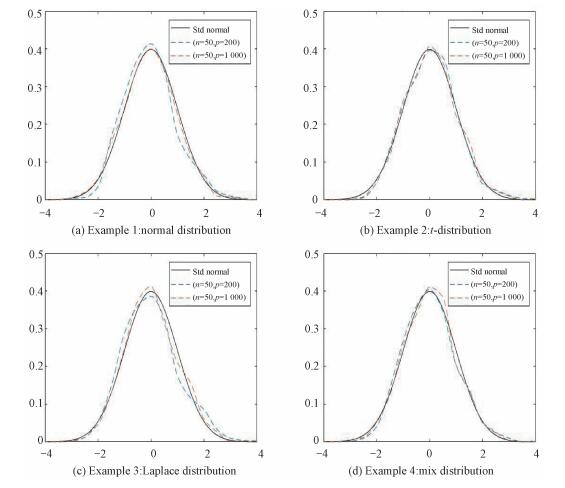
Moreover, we plot the empirical distributions of SR with the settings of four examples and compare them with the standard normal distribution. And, Fig. 1 confirms the asymptotic normal distributions of SR given in Theorem 1.1.
|
Download:
|
|
Fig. 1 Tn under the null hypothesis with four different distributions of X |
|
In this section, we employ the proposed signed-rank-based method to study an ophthalmic data. This data is collected by the Beijing Tongren Eye Center and Anyang Eye Hospital. We take the data of the fifth and sixth grades of a class in the data, Apply the proposed method to study whether the visual factors and their interaction with eye habits are different in different grades.
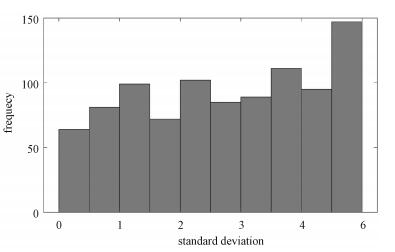
Firstly, we remove the visual factors and their interaction with eye habits with missing values greater than 15%, and impute the sample mean into the missing values for the remaining 945 factors. Then, we let Xi be the difference between the visual factors and their interaction with eye habits of the i-th student in the sixth grade and those in the fifth grade. And, we calculate standard deviations of each dimension in X, and show the distribution of the standard deviations in Fig. 2. It shows that these standard deviations are different, so the scalar-invariance method are supposed to have better performance in the analysis of this data. [JP2]Applying the proposed SR method, we obtain a p-value < 10-9, which illustrates that the visual factors and their interaction factors of eye habits are different in different grades. Through CQ, WPL and FZW methods, the p-values obtained are 0.491 0, 0.491 3 and < 10-9 respectively. For the standard deviations of each dimension in the sample are different, the CQ and WPL methods are relatively ineffective, while the p -values obtained through FZW and SR methods are small.
|
Download:
|
|
Fig. 2 The distribution of the standard deviations |
|
| [1] |
Bai Z D, Hewa S. Effect of high dimension: by an example of a two sample problem[J]. Statistica Sinica, 1996, 6(2): 311-329. |
| [2] |
Chen S X, Qin Y L. A two sample test for high dimensional data with applications to gene-set testing[J]. Annals of Statistics, 2010, 38(2): 808-835. DOI:10.1214/09-aos716 |
| [3] |
Srivastava M S, Meng D. A test for the mean vector with fewer observations than the dimension[J]. Journal of Multivariate Analysis, 2008, 99(3): 386-402. DOI:10.1016/j.jmva.2006.11.002 |
| [4] |
Srivastava M S. A test for the mean vector with fewer observations than the dimension under non-normality[J]. Journal of Multivariate Analysis, 2009, 100(3): 518-532. DOI:10.1016/j.jmva.2008.06.006 |
| [5] |
Srivastava M S, Shota K, Yutaka K. A two sample test in high dimensional data[J]. Journal of Multivariate Analysis, 2013, 114: 349-358. DOI:10.1016/j.jmva.2012.08.014 |
| [6] |
Park J Y, Deepak N A. A test for the mean vector in large dimension and small samples[J]. Journal of Statistical Planning and Inference, 2013, 143(5): 929-943. DOI:10.1016/j.jspi.2012.11.001 |
| [7] |
Wang L, Peng B, Li R Z. A high-dimensional nonparametric multivariate test for mean vector[J]. Journal of the American Statistical Association, 2015, 110(512): 1658-1669. DOI:10.1080/01621459.2014.988215 |
| [8] |
Feng L, Zou C L, Wang Z J. Multivariate-sign-based high-dimensional tests for the two-sample location problem[J]. Journal of the American Statistical Association, 2016, 111(514): 721-735. DOI:10.1080/01621459.2015.1035380 |
 2022, Vol. 39
2022, Vol. 39 


