2. Key Laboratory of Big Data Mining and Knowledge Management, Chinese Academy of Sciences, Beijing 100049, China;
3. Beijing Tongren Eye Center, Beijing Tongren Hospital, Beijing Ophthalmology & Visual Science Key Laboratory, Beijing Institute of Ophthalmology, Capital Medical University, Beijing 100730, China
2. 中国科学院大数据挖掘与知识管理重点实验室, 北京 100049;
3. 首都医科大学附属北京同仁医院北京同仁眼科中心, 北京眼科及视光学重点实验室, 北京 100730
The classification problem of ordinal response data, examples of this including cancer patients grouped in early, mediocre and terminal stages, customers grouped into low, middle and high credit levels, are widely discussed in recent years. Some methods[1-3] have been proposed to solve the problem. A direct method for ordinal response data is to convert ordinal labels to numerical values, such as the conversion of {excellent, good, moderate, poor} to {1, 2, 3, 4}. As a result, a regression method can be applied to the converted dataset. However, not all class labels can be converted to positive integers. Another method is to convert class labels to common numerical value rather than positive integers by a map. Nevertheless, it is difficult to define the mapping function. Frank and Hall[4] proposed a method that converted ordinal classification problem to several binary classification problems. For each i∈{0, 1, 2, 3, …, K}, each sample is classified between the meta-class including classes 0 to i and the meta-class including classes i+1 to K. The final classification result can be inferred from the K binary predictions. Shashua and Levin[5] extended SVM for ordinal regression by finding K ordinal thresholds, namely b1≤b2≤…≤bK, spliting the real line into K+1 ordinal parts. Wang et al.[6] proposed nonparallel support vector for ordinal regression by constructing a hyperplane in each class. However, these methods perform poorly when the ordinal label is mislabeled.
More and more literatures studied mislabeled response data by means of binary logistic regression[7]. Tian and Sun[8] proposed a new fuzzy set method to detect suspectable mislabeled points, and then delete their labels and construct a semi-supervised model. Logistic regression based on different mislabel probabilities are also widely used to mislabeled unordered response data. Copas considered equal and constant mislabel probabilities[9] and Komori et al.[10] assumed mislabeling occurs only the 0-group. In addition, Hung et al.[7] proposed a robust mislabel logistic regression based on γ-divergence with the property of strong robustness in dealing with binary mislabeled response data. Neverthelss, above studies is not suitable to mislabeled ordinal response data.
In this article, we apply γ-divergence to ordinal multiple classification logistic regression and construct a robust ordinal mislabel logistic regression model, which not only possess the strong robustness but also the mislabel probabilities need not to be modeled. Our method have better effectiveness on ordinal mislabeled response data. It is noted that although γ-divergence has been previously adopted for regression analysis, to the best of our knowledge, γ-divergence has never been applied to ordinal response data.
1 MethodologyGiven a dataset {(xi, y0i), i=1, 2, …, n} in binary logistic regression, where xi∈
Suppose there are K+1 ordered classes {0, 1, 2, …, K}, πj(x)=P(y0=j|X=x). Consider the event that an observation belongs to the meta-class {0, 1, …, j}, that is y0∈{0, 1, …, j}, whose probability is
| $ \begin{aligned} &\operatorname{logit}\left[\pi_{0}(\boldsymbol{x})+\pi_{1}(\boldsymbol{x})+\pi_{2}(\boldsymbol{x})+\cdots+\pi_{j}(\boldsymbol{x})\right] \\ &=\log \left[\frac{\pi_{0}(\boldsymbol{x})+\pi_{1}(\boldsymbol{x})+\pi_{2}(\boldsymbol{x})+\cdots+\pi_{j}(\boldsymbol{x})}{\pi_{j+1}(\boldsymbol{x})+\pi_{j+2}(\boldsymbol{x})+\cdots+\pi_{K}(\boldsymbol{x})}\right] \\ &=\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{x}+b_{j+1}, j=0, \cdots, K-1 . \end{aligned} $ | (1) |
And the coefficient vector β=(β1, β2, …, βp)T is the same for all j in equation (1). Their intercept terms b1, b2, …, bK split the plane into K+1 ordinal parts. Therefore, we only need to estimate parameters β, b1, b2, …, bK, and βj+1=(βT, bj+1)T denotes (j+1)-th hyperplane, j=0, 1, 2, …, K-1.
According to Eq.(1), we obtain the category probability functions as follows:
| $ \left\{\begin{array}{l} \pi_{0}\left(\boldsymbol{x} ; \boldsymbol{\beta}, b_{1}, \cdots, b_{K}\right)=\frac{A \exp \left(b_{1}\right)}{D} \\ \ \ \ \ \ \ \ \ \Pi_{h=2}^{K}\left[1+A \exp \left(b_{h}\right)\right], \\ \pi_{j}\left(\boldsymbol{x} ; \boldsymbol{\beta}, b_{1}, \cdots, b_{K}\right)=\frac{1}{D}\left[A \exp \left(b_{j+1}\right)-A \exp \left(b_{j}\right)\right] \\ \ \ \ \ \ \ \ \ \Pi_{l=1, l \neq j, l \neq j+1}^{K}\left[1+A \exp \left(b_{l}\right)\right], \\ \ \ \ \ \ \ \ \ j=1, \cdots, K-1, \\ \pi_{K}\left(\boldsymbol{x} ; \boldsymbol{\beta}, b_{1}, \cdots, b_{K}\right)=\frac{1}{D} \Pi_{h=1}^{K-1}\left[1+A \exp \left(b_{h}\right)\right], \end{array}\right. $ | (2) |
where
Let g be the data generating probability density function and fθ be the model probability density function indexed by the parameter θ, the γ-divergence between g and fθ is defined as[7]
| $ D_{\gamma}\left(g, f_{\boldsymbol{\theta}}\right)=\frac{1}{\gamma(\gamma+1)}\left\{\|g\|_{\gamma+1}-\int\left(\frac{f_{\boldsymbol{\theta}}}{\left\|f_{\boldsymbol{\theta}}\right\|_{\gamma+1}}\right)^{\gamma} g\right\}, $ | (3) |
where
| $ \|g\|_{\gamma+1}=\left(\int g^{\gamma+1}\right)^{\frac{1}{\gamma+1}},\left\|f_{\boldsymbol{\theta}}\right\|_{\gamma+1}=\left(\int f_{\boldsymbol{\theta}}^{\gamma+1}\right)^{\frac{1}{\gamma+1}}. $ |
In the limiting case,
In the presence of contamination, g=εfθ*+(1-ε) τ, θ* is the true model parameter, 1-ε is the contamination proportion and τ is the contamination density function. The estimation criterion of the minimum γ-divergence estimates parameter by minimizing Dγ(g, fθ), which is equivalent to minimizing
| $ \varepsilon D_{\gamma}\left(f_{\boldsymbol{\theta}^{*}}, f_{\boldsymbol{\theta}}\right)-\frac{H_{\gamma}(\varepsilon, \tau ; \boldsymbol{\theta})}{\gamma(\gamma+1)}, $ |
by taking the actual g into Eq.(3) and ignoring the terms which not involve θ, where Hγ(ε, τ; θ)=(1-ε)
Remark 1.1 Suppose that
Consider n independent samples and combine the discussions of Hγ(ε, τ; θ), the empirical version of the γ-divergence loss function[7] is
| $ L(\boldsymbol{\theta})=-\frac{1}{n} \sum\limits_{i=1}^{n} \frac{f\left(y_{i} \mid \boldsymbol{x}_{i} ; \boldsymbol{\theta}\right)^{\gamma}}{\left\|f\left(\cdot \mid \boldsymbol{x}_{i} ; \boldsymbol{\theta}\right)\right\|_{\gamma+1}}, $ | (4) |
where
In conventional ordinal logistic regression model with K+1 classes, namely y0∈{0, 1, …, K}, the probability density function
| $ f\left(y_{0} \mid \boldsymbol{x} ; \boldsymbol{\beta}, b_{1}, \cdots, b_{K}\right)=\prod\limits_{j=0}^{K} \pi_{j}^{Y_{0 j}}\left(\boldsymbol{x} ; \boldsymbol{\beta}, b_{1}, \cdots, b_{K}\right), $ | (5) |
for y0, where πj(x; β, b1, …, bK), j=0, 1, …, K given by the (2), and y0 can be recorded by K random variables (Y01, Y02, …, Y0K), where (0, 0, 0, …, 0) denotes y0=0, y0=j when Y0j=1, Y0k=0, j≠k. On the basis of (4), the robust estimator
| $ \begin{gathered} F\left(\boldsymbol{\beta}, b_{1}, \cdots, b_{K}\right)\\ =-\frac{1}{n} \sum\limits_{i=1}^{n}\left(\frac{f\left(y_{i} \mid \boldsymbol{x}_{i} ; \boldsymbol{\beta}, b_{1}, \cdots, b_{K}\right)}{\left\|f\left(\cdot \mid \boldsymbol{x}_{i} ; \boldsymbol{\beta}, b_{1}, \cdots, b_{K}\right)\right\|_{1+\gamma}}\right)^{\gamma}, \end{gathered} $ | (6) |
where
| $ \begin{gathered} \left\|f\left(\cdot \mid \boldsymbol{x} ; \boldsymbol{\beta}, b_{1}, \cdots, b_{K}\right)\right\|_{1+\gamma} \\ =\left\{\sum\limits_{j=0}^{K}\left[\pi_{j}\left(\boldsymbol{x} ; \boldsymbol{\beta}, b_{1}, \cdots, b_{K}\right)\right]^{1+\gamma}\right\}^{\frac{1}{1+\gamma}} . \end{gathered} $ |
Direct differentiation of the objective function F(β, b1, …, bK) leads to the parameters estimation equations
| $ S_{\gamma}(\boldsymbol{\beta})=-\frac{\gamma}{1+\gamma} \cdot \frac{1}{n} \sum\limits_{i=1}^{n} \omega_{\gamma i}\left(\frac{\frac{(1+\gamma) \partial C_{i}}{\partial \boldsymbol{\beta}}}{C_{i}}-\frac{\frac{\partial B_{i}}{\partial \boldsymbol{\beta}}} {B_{i}}\right), $ | (7) |
| $ S_{\gamma}\left(b_{j}\right)=-\frac{\gamma}{1+\gamma} \cdot \frac{1}{n} \sum\limits_{i=1}^{n} \omega_{\gamma i}\left(\frac{\frac{(1+\gamma) \partial C_{i}}{\partial b_{j}}}{C_{i}}-\frac{\frac{\partial B_{i}}{\partial b_{j}}}{B_{i}}\right), $ | (8) |
with the weight function
| $ {\omega}_{\gamma i}=\left(\frac{C_{i}^{1+\gamma}}{{B}_{i}}\right)^{\frac{\gamma}{\gamma+1}}, $ | (9) |
and where
| $ \begin{aligned} &B_{i}=\\ &\sum\limits_{j=1}^{K-1}\left\{\left[A_{i}\left(\exp \left(b_{j+1}\right)-\exp \left(b_{j}\right)\right)\right] \prod\limits_{l=1,\atop {l \neq j,\atop l \neq j+1}}^{K}\left[1+A_{i} \exp \left(b_{l}\right)\right]\right\}^{1+\gamma}+\\ &\left[A_{i} \exp \left(b_{1}\right) \prod\limits_{h=2}^{K}\left(1+A_{i} \exp \left(b_{h}\right)\right)\right]^{1+\gamma}+\prod\limits_{j=1}^{K-1}\left[1+A_{i} \exp \left(b_{j}\right)\right]^{1+\gamma}, \end{aligned} $ | (10) |
| $ \begin{aligned} &C_{i}= \\ &\sum\limits_{j=1}^{K-1}\left\{Y_{i j}\left[A_{i}\left(\exp \left(b_{j+1}\right)-\exp \left(b_{j}\right)\right)\right] \prod\limits_{\substack{l=1, \atop {l \neq j,\atop l \neq j+1}}}^{K}\left[1+A_{i} \exp \left(b_{l}\right)\right]\right\}+ \\ &\left(1-\sum\limits_{j=1}^{K} Y_{i j}\right) A_{i} \exp \left(b_{1}\right) \prod\limits_{h=2}^{K-1}\left[1+A_{i} \exp \left(b_{h}\right)\right]+ \\ &Y_{i K} \prod\limits_{h=1}^{K-1}\left[1+A_{i} \exp \left(b_{h}\right)\right] \end{aligned} $ | (11) |
When γ=0, the above estimation equation degenerates to the estimation equation of conventional ordinal logistic regression with non-robust estimator. From (7)-(9), the robustness of
Remark 1.2 The weight of x in the parameter estimation equation is
Due to the complexity of the second derivative of the objective function based on γ-divergence, in this paper, we adopt the gradient descent algorithm to solve model, which is summarized in Algorithm 1.
Algorithm 1 Gradient descent algorithm
Require: The dataset: (xi, yi), i=1, 2, …, n, the tuning parameter: γ.
Ensure: The regression coefficients: β, b1, b2, …, bK. Initializing the s=0, ε=10-3 and given an initial value β(0), bj(0), j=1, 2, …, K.
repeat
s=s+1;
for k=1, 2, …, p do
end for
for j=1, 2, …, K do
end for
Where β=(β1, β2, …, βp)T, b=(b1, b2, …, bK)T, ωγi, Bi, Ci are defined as (9)-(11), α is the step length obtained by Armijo search. We consider three classification problem in our simulation study, the calculation results of
until
returnβT(s+1), bT(s+1).
The proposed objective function has a complex form, so it is difficult to establish the convergence property. Experimental results demonstrate that, for all of our simulated and real datasets, convergence is successfully achieved within 50 overall iterations (mostly within 20 iterations).
The definition of γ-divergence and studies suggest that γ balances between robustness and efficiency. However, Fujisawa and Eguchi[12] said there could be not consistent best way to select an appropriate tuning parameter γ. In practice, there are some methods to select the tuning parameter γ, such as the adaptive selection procedure by Mollah et al.[13], the cross validation[14] and a sequence of the parameter[15]. In this article, we consider a sequence of γ as 1, 2, 3, 4 and 5 following Zang et al.[15], and proceed the simulation study under each determined γ.
2 Simulation studiesIn the numerical simulation study, we consider ordinal three classification problem with possibly mislabeling, that's to say, the labels of ordinal response datas y∈{0, 1, 2}, then π0(x), π1(x), π2(x), the probability density function f(y|x; β, b1, b2), and Ci, Bi, Ai can be obtained by the (2), (5), (10)-(11), and the calculation results of them are placed in Appendix (A7)-(A13). Simulation results are reported with 500 replicates in the simulation studies.
2.1 Simulation settingsIn each simulation run, we generate 300 random samples xs in
1) the explanatory variables are independent, i.e. Σ=I,
2) the auto-regressive correlation (AR) given by σij=ρ|i-j | with ρ=0.5 and ρ=0.75,
3) the banded correlation (Band) given by σij=ρ|i-j | with ρ=0.6 if |i-j|≤2, ρ=0 if |i-j|>2.
We generate ordered mislabeled labels {0, 1, 2} in the light of the following settings of mislabel probabilities:
| $ \left\{\begin{array}{l} \eta_{01}=\eta_{10}=m / 2, \\ \eta_{12}=\eta_{21}=m / 2, \\ \eta_{02}=\eta_{20}=m / 4, \end{array}\right. $ | (12) |
where
| $ \eta_{i j}=P\left(y=j \mid y_{0}=i, \boldsymbol{X}=\boldsymbol{x}\right), i, j=0,1,2. $ |
We assume m={0.1, 0.15, 0.2, 0.25, 0.3} in the simulation. Considering the mislabel probabilities, the labels can be generated by following formulas:
| $ \left\{\begin{array}{l} P(y=0 \mid \boldsymbol{X}=\boldsymbol{x})=\left(1-\eta_{01}-\eta_{02}\right) \pi_{0}+\eta_{10} \pi_{1}+\eta_{20} \pi_{2}, \\ P(y=1 \mid \boldsymbol{X}=\boldsymbol{x})=\left(1-\eta_{10}-\eta_{12}\right) \pi_{1}+\eta_{01} \pi_{0}+\eta_{21} \pi_{2}, \\ P(y=2 \mid \boldsymbol{X}=\boldsymbol{x})=\left(1-\eta_{20}-\eta_{21}\right) \pi_{2}+\eta_{02} \pi_{0}+\eta_{12} \pi_{1} . \end{array}\right. $ | (13) |
We apply the robust ordinal mislabel logistic regression method on the simulated dataset. And we compare the conventional ordinal logistic regression (COLR) method which takes no account of mislabeling with the robust ordinal mislabel logistic regression (robust ordinal mislabel) method from different aspects. Firstly, we evaluate the two methods via two indexes, i.e. the mean absolute error (MAE) and standard deviation (SD) of the estimates of β, b1, b2. Secondly, we compare the classification accuracy of the two methods on 800 test samples. The true values, namely β0, b01, b02 follow the first part of uniform distribution [-1, 0.5] and the last part of uniform distribution [0.5, 1], and β01=(β0T, b01)T, β02=(β0T, b02)T are two parallel classification hyperplanes. Partial results are presented in the article.
Figure 1 displays the variation of classification error rate of 800 test samples with m under different structures of Σ. It can be seen clearly that the classification error rate obtained by COLR method increases more greatly than the classification error rate acquired by robust ordinal mislabel method with the increase of the mislabel probability (MP). Furthermore, we can select γ by the performance of classification from Fig. 1. We can also note that there exists the best effectiveness when γ=4.
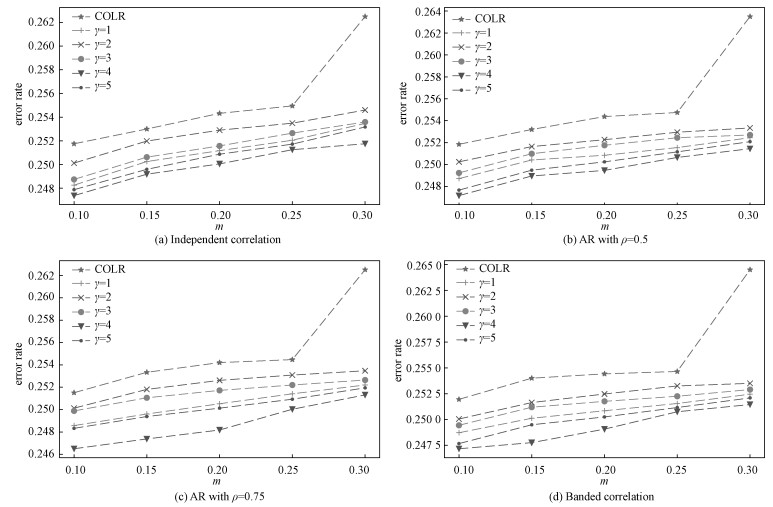
|
Download:
|
|
Fig. 1 Variation of classification error rate with m under different Σ |
|
When Σ=I, the comparisons between the true values and the estimates of β, b1, b2 under different γ and m are presented in Fig. 2 (a)-Fig. 2 (d) and the comparisons between the true values and the estimates of β, b1, b2 under different γ and m are displayed in Fig. 2 (e)-Fig. 2 (h) when the structure of Σ is AR with ρ=0.5. Figure 2 show that, for all given m and γ and the structure of Σ is AR (ρ=0.5) or I, the estimates of β, b1, b2 from the robust ordinal mislabel method are closer to the true values of β, b1, b2 than from COLR method.

|
Download:
|
|
Fig. 2 The comparisons between the true values and the estimates of β, b1, b2 under different settings |
|
When the structure of Σ is Band, MAE of parameter estimation under different γ and m values are displayed in Fig. 3 (a)-Fig. 3 (d). When the structure of Σ is AR with ρ=0.75, the MAE of parameter estimation are presented in Fig. 3 (e)-Fig. 3 (h). Figure 3 illustrate that the MAE of parameter estimation from the robust ordinal mislabel method is smaller than from COLR method. Both Fig. 2 and Fig. 3 demonstrate the robust ordinal mislabel method possesses better performance in estimating coefficients of the classification hyperplanes.
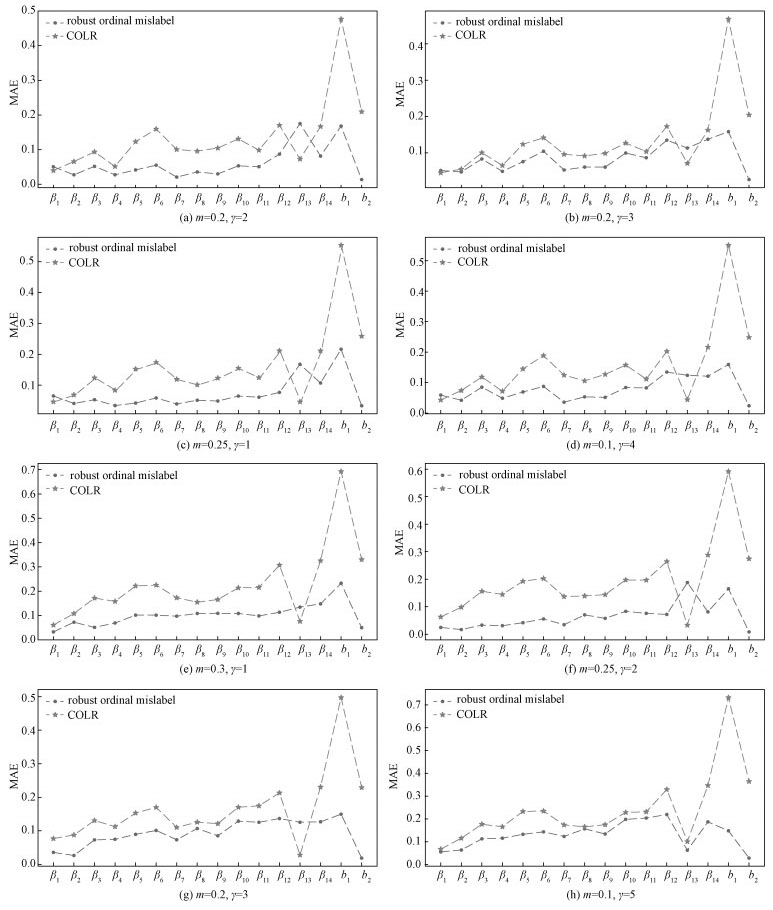
|
Download:
|
|
Fig. 3 The comparisons of MAE from two methods under different settings |
|
Table 1 displays MAE of parameter estimation and SD of the estimates from the COLR method and the robust ordinal mislabel method under different Σ, MP and γ values. We can obviously find that the MAE and the SD from robust ordinal mislabel method are smaller than from COLR method respectively. It also demonstrates that the robust ordinal mislabel method performs well and more robustly than COLR method in estimating coefficients.
|
|
Table 1 MAE and SD from two methods under different settings |
In addition, we verify the effectiveness of the proposed method on samples conforming to the heavy tailed distribution, such as t-distribution, mixture of normal distribution. In each simulation, we generate two groups of random samples xs in
When γ=4 and xs are from the mixture of normal distribution, the MAE and SD of parameter estimation are displayed in Table 2. When γ=2 and xs are from the distribution t(0, Σ, 3), the MAE and SD of parameter estimation are displayed in Table 3. From the resluts, we can obviously find that both MAE and SD from the COLR mtehod are larger than both MAE and SD from the robust ordinal mislabel method when xs are from heavy tailed distributions. This also means that the robust ordinal mislabel method has better effectiveness than COLR method in estimating coefficients. Simultaneously, we can find from the Table 2 and Table 3 that MAE of parameter estimation is smaller when samples are from normal distribution in contrast with the situation that samples are from t-distribution or mixture of normal distribution.
|
|
Table 2 MAE and SD from two methods under different distributions of X |
|
|
Table 3 MAE and SD from two methods under different distributions of X |
In this section, we demonstrate the effectiveness of the proposed method on real data. Our dataset, i.e. the childhood eye data, is from Beijng Tongren Hospital[16], which contains 6 years of data from the first grade to sixth grade, and the variables include ocular biometry, near work, food habits, living habits, habits of wearing spectacles in this school year, accommodative response, times outdoors, and parental myopia and so on.
In the childhood vision research, we regard the change of spherical equivalent (CSE) after mydriasis from first grade to sixth grade as dependent variable. We divide the range of myopia into high myopia, moderate myopia and low myopia. The CSE < -2.5 denotes high myopia, corresponding to class 2 and the label is 2 in this class. The -2.5≤ CSE≤-1.5 denotes moderate myopia and corresponds to class 1. The CSE>-1.5 denotes low myopia and corresponds to class 0. The level of myopia is an ordinal response data and spherical equivalent might be inaccurate because of limitation of mydriasis examination, so there might be some mislabeled responses in the data.
We use the factors of vision from the first grade students as the independent variables to construct regression model, which can analyze the effectivenss of variables on the myopia progression in primary school. These variables are divided into three categories: continuous variables, nominal variables and multi-class variables. The data used in the model contains 1 370 samples and 28 independent variables and the meanings of the variables are presented in Appendix B.
We analyse the real data from two cases.
Example 3.1 (assessment of robustness) We first delete 10 % samples before running and then calculate the mean (Mean) and SD of ten runs of each variable. The Mean and SD are presented in Table 4. Our method performs more robustly than COLR by SD obviously. Most important variables[17], such as "AL", "SE", "DUCVA", "D_COMR2", "BREAK3", have smaller SD by means of robust ordinal mislabel method than COLR method. It demonstrates that our method have strong stability.
|
|
Table 4 The Mean and SD of the variables from two methods |
Example 3.2 We take the Mean as the estimates of β, b1, b2. The absolute value of the Mean can reflect the importance of variables. Our method can better reflect the importance of important variables, such as "AL", "SE", which are regarded as important variables[18], having greater absolute estimate with the help of robust ordinal mislabel method than COLR method. "LT" is positively correlated with the degree of myopia[19]. However, the estimate of it from robust ordinal mislabel method is positive than from COLR method is negative. It shows that the robust ordinal mislabel method proposed in the paper can more accurately reflect the relationship between independent variables and dependent variables. In addition, "K1" is negatively correlated with the degree of myopia. It can reflect this point from the case of γ=1, 4, 5. However, the case of γ=2, 3 can not reflect the situation. The absolute value of the estimate of "K1" is the largest for the case of γ=4 and the result is consistent with classification error rate under different γ.
4 Conclusion and future workIn this paper, we proposed a robust ordinal mislabel logistic regression method based on γ-divergence. The model is obtained by minimizing γ-divergence estimation. Both theoretical analysis and simulation studies make clear that the proposed method is quite efficient for solving classification problems with ordinal and mislabeled response data. Firstly, the mislabel probabilities need not to be modeled in our method. Secondly, our method performs more robustly than conventional ordinal logistic regression by the ways of simulation results and real data analysis. However, the robust ordinal mislabel logistic regression based on γ-divergence is applied to low dimensional data. There exists mislabeled response data on some high dimensional ordinal data, we can consider further research for ordinal mislabel method to high dimensional data.
Appendices Appendix AWe consider ordinal three classification problem in simulation studies, the
| $ \frac{\partial C_{i}}{\partial b_{1}}=\left(1-Y_{i 1}-Y_{i 2}\right) A_{i} \exp \left(b_{1}\right)\left(1+A_{i} \exp \left(b_{2}\right)\right)-Y_{i 1} A_{i} \exp \left(b_{1}\right)+Y_{i 2} A_{i} \exp \left(b_{2}\right). $ | (A1) |
| $ \begin{gathered} \frac{\partial B_{i}}{\partial b_{1}}=\left\{-\left[A_{i}\left(\exp \left(b_{2}\right)-\exp \left(b_{1}\right)\right)\right]^{\gamma} A_{i} \exp \left(b_{1}\right)+\left(1+A_{i} \exp \left(b_{1}\right)\right)^{\gamma} A_{i} \exp \left(b_{1}\right)+\right. \\ \left.\left[A_{i} \exp \left(b_{1}\right)\left(1+A_{i} \exp \left(b_{2}\right)\right)\right]^{1+\gamma}\right\}(1+\gamma) . \end{gathered} $ | (A2) |
| $ \frac{\partial C_{i}}{\partial b_{2}}=\left(1-Y_{i 1}-Y_{i 2}\right) A_{i}^{2} \exp \left(b_{1}+b_{2}\right)+Y_{i 1} A_{i} \exp \left(b_{2}\right) . $ | (A3) |
| $ \frac{\partial B_{i}}{\partial b_{2}}=\left\{\left[A_{i}\left(\exp \left(b_{2}\right)-\exp \left(b_{1}\right)\right)\right]^{\gamma} A_{i} \exp \left(b_{2}\right)+\left[A_{i} \exp \left(b_{1}\right)\left(1+A_{i} \exp \left(b_{2}\right)\right)\right]^{\gamma} A_{i}^{2} \exp \left(b_{1}+b_{2}\right)\right\}(\gamma+1). $ | (A4) |
| $ \begin{gathered} \frac{\partial C_{i}}{\partial \beta_{k}}=\left\{Y_{i 1}\left[A_{i}\left(\exp \left(b_{2}\right)-\exp \left(b_{1}\right)\right)\right]+Y_{i 2} A_{i} \exp \left(b_{1}\right)+\right. \\ \left.\left(1-Y_{i 1}-Y_{i 2}\right)\left[A_{i}^{2} \exp \left(b_{1}+b_{2}\right)+A_{i} \exp \left(b_{1}\right)\left(1+A_{i} \exp \left(b_{2}\right)\right)\right]\right\} x_{i j} \cdot \end{gathered} $ | (A5) |
| $ \begin{gathered} \frac{\partial B_{i}}{\partial \beta_{k}}=(1+\gamma)\left\{\left[A_{i}\left(\exp \left(b_{2}\right)-\exp \left(b_{1}\right)\right)\right]^{\gamma+1}+A_{i} \exp \left(b_{1}\right)\left(1+A_{i} \exp \left(b_{1}\right)\right)^{\gamma}+\right. \\ \left.\left[A_{i} \exp \left(b_{1}\right)\left(1+A_{i} \exp \left(b_{2}\right)\right)\right]^{1+\gamma}+\left[A_{i} \exp \left(b_{1}\right)\left(1+A_{i} \exp \left(b_{2}\right)\right)\right]^{\gamma} A_{i} \exp \left(b_{1}+b_{2}\right)\right\} x_{i j}. \end{gathered} $ | (A6) |
| $ \pi_{0}=P\left(y_{0}=0 \mid \boldsymbol{X}=\boldsymbol{x}\right)=\frac{A \exp \left(b_{1}\right)}{1+A \exp \left(b_{1}\right)}. $ | (A7) |
| $ \pi_{1}=P\left(y_{0}=1 \mid \boldsymbol{X}=\boldsymbol{x}\right)=\frac{A \exp \left(b_{2}\right)}{1+A \exp \left(b_{2}\right)}-\frac{A \exp \left(b_{1}\right)}{1+A \exp \left(b_{1}\right)} . $ | (A8) |
| $ \pi_{2}=P\left(y_{2}=2 \mid \boldsymbol{X}=\boldsymbol{x}\right)=\frac{1}{1+A \exp \left(b_{2}\right)}. $ | (A9) |
The objective function:
| $ F\left(\boldsymbol{\beta}, b_{1}, b_{2}\right)=-\frac{1}{n} \sum\limits_{i=1}^{n}\left(\frac{f\left(y_{i} \mid \boldsymbol{x}_{i} ; \boldsymbol{\beta}, b_{1}, b_{2}\right)}{\left\|f\left(\cdot \mid \boldsymbol{x}_{i} ; \boldsymbol{\beta}, b_{1}, b_{2}\right)\right\|}_{1+\gamma}\right)^{\gamma}=-\frac{1}{n} \sum\limits_{i=1}^{n}\left(\frac{C_{i}^{1+\gamma}}{B_{i}}\right)^{\frac{\gamma}{1+\gamma}}, $ | (A10) |
where
| $ A_{i}=\exp \left(\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{x}_{i}\right), $ | (A11) |
| $ B_{i}=\left\{A_{i} \exp \left(b_{1}\right)\left[1+A_{i} \exp \left(b_{2}\right)\right]\right\}^{1+\gamma}+\left[A_{i}\left(\exp \left(b_{2}\right)-\exp \left(b_{1}\right)\right)\right]^{1+\gamma}+\left[1+A_{i} \exp \left(b_{1}\right)\right]^{1+\gamma}, $ | (A12) |
| $ C_{i}=\left(1-Y_{i 1}-Y_{i 2}\right) A_{i} \exp \left(b_{1}\right)\left[1+A_{i} \exp \left(b_{2}\right)\right]+Y_{i 1}\left[A_{i}\left(\exp \left(b_{2}\right)-\exp \left(b_{1}\right)\right)\right]+Y_{i 2}\left[1+A_{i} \exp \left(b_{1}\right)\right]. $ | (A13) |
The meanings of the variables in Table 4 are as follows. The level number after some variable name is the result of the dummy variable processing.
Binary variables (1: yes, 0: no):
MOTHER_A: Whether the natural mother has amblyopia?
GLASS: Do you wear glasses?
DESK_L: When you are reading or doing close work, do you use a desk lamp?
OMT: Do your children have received the other myopia treatment?
TUTOR2: Do your children take part in the tutoring class in their spare time (indoor learning class)?
GENDER: Is gender a woman?
Ordinal variables (1:lower, 4:upper):
COLA: Quantity of drinking a carbonated drink frequency in the last 4 weeks.
EGGEAT: Quantity of eating eggs frequency in the last 4 weeks.
MEATS: Quantity of eating meat frequency in the last 4 weeks.
READLY: Quantity of weekly reading.
BREAK: Quantity of keeping reading or doing close work frequency.
D_COMR: When your child uses a computer, distance from computer from the computer (1:nearer, 4:farer).
Continuous variables:
MYOPICS: The number of myopia parents.
K2: The steep keratometry readings.
SE: Spherical equivalent after mydriasis.
AR: Accommodative response.
DUCVA: Distant uncorrected visual acuity.
PUPIL_SIZE: Pupil diameter.
AL: Axial length.
BL: Birth length.
LT: Lens thickness.
NUCVA: Near uncorrected visual acuity.
K1: The flat keratometry readings.
| [1] |
Dembczyński K, Kotłowski W, Słowiński R. Ordinal classification with decision rules[C]//International Workshop on Mining Complex Data. Springer, Berlin, Heidelberg, 2007: 169-181. DOI: 10.1007/978-3-540-68416-9_14.
|
| [2] |
Cardoso J S, Costa J F. Learning to classify ordinal data: the data replication method[J]. Journal of Machine Learning Research, 2007, 8(Jul): 1393-1429. |
| [3] |
Chang K Y, Chen C S, Hung Y P. A ranking approach for human ages estimation based on face images[C]//2010 20th International Conference on Pattern Recognition. August 23-26, 2010, Istanbul, Turkey. IEEE, 2010: 3396-3399. DOI: 10.1109/ICPR.2010.829.
|
| [4] |
Frank E, Hall M. A simple approach to ordinal classification[C]//European Conference on Machine Learning. Springer, Berlin, Heidelberg, 2001: 145-156. DOI: 10.1007/3-540-44795-4_13.
|
| [5] |
Shashua A, Levin A. Ranking with large margin principle: two approaches[C]//Advances in Neural Information Processing Systems. 2003: 961-968.
|
| [6] |
Wang H D, Shi Y, Niu L F, et al. Nonparallel support vector ordinal regression[J]. IEEE Transactions on Cybernetics, 2017, 47(10): 3306-3317. DOI:10.1109/TCYB.2017.2682852 |
| [7] |
Hung H, Jou Z Y, Huang S Y. Robust mislabel logistic regression without modeling mislabel probabilities[J]. Biometrics, 2018, 74(1): 145-154. DOI:10.1111/biom.12726 |
| [8] |
Tian Y, Sun M, Deng Z B, et al. A new fuzzy set and nonkernel SVM approach for mislabeled binary classification with applications[J]. IEEE Transactions on Fuzzy Systems, 2017, 25(6): 1536-1545. DOI:10.1109/TFUZZ.2017.2752138 |
| [9] |
Qian W M, Li Y M. Parameter estimation in linear regression models for longitudinal contaminated data[J]. Applied Mathematics: A Journal of Chinese Universities, 2005, 20(1): 64-74. DOI:10.1007/s11766-005-0038-0 |
| [10] |
Komori O, Eguchi S, Ikeda S, et al. An asymmetric logistic regression model for ecological data[J]. Methods in Ecology and Evolution, 2016, 7(2): 249-260. DOI:10.1111/2041-210X.12473 |
| [11] |
Cox C. Location-scale cumulative odds models for ordinal data: a generalized non-linear model approach[J]. Statistics in Medicine, 1995, 14(11): 1191-1203. DOI:10.1002/sim.4780141105 |
| [12] |
Fujisawa H, Eguchi S. Robust parameter estimation with a small bias against heavy contamination[J]. Journal of Multivariate Analysis, 2008, 99(9): 2053-2081. DOI:10.1016/j.jmva.2008.02.004 |
| [13] |
Mollah M N H, Eguchi S, Minami M. Robust prewhitening for ICA by minimizing β-divergence and its application to FastICA[J]. Neural Processing Letters, 2007, 25(2): 91-110. DOI:10.1007/s11063-006-9023-8 |
| [14] |
Smith S A, O'Meara B C. treePL: divergence time estimation using penalized likelihood for large phylogenies[J]. Bioinformatics, 2012, 28(20): 2689-2690. DOI:10.1093/bioinformatics/bts492 |
| [15] |
Zang Y G, Zhao Q, Zhang Q Z, et al. Inferring gene regulatory relationships with a high-dimensional robust approach[J]. Genetic Epidemiology, 2017, 41(5): 437-454. DOI:10.1002/gepi.22047 |
| [16] |
Kakita T, Hiraoka T, Oshika T. Influence of overnight orthokeratology on axial elongation in childhood myopia[J]. Investigative Ophthalmology & Visual Science, 2011, 52(5): 2170-2174. DOI:10.1167/iovs.10-5485 |
| [17] |
Hoyt C S, Stone R D, Fromer C, et al. Monocular axial myopia associated with neonatal eyelid closure in human infants[J]. American Journal of Ophthalmology, 1981, 91(2): 197-200. DOI:10.1016/0002-9394(81)90173-2 |
| [18] |
Li S M, Liu L R, Li S Y, et al. Design, methodology and baseline data of a school-based cohort study in Central China: the Anyang childhood eye study[J]. Ophthalmic Epidemiology, 2013, 20(6): 348-359. DOI:10.3109/09286586.2013.842596 |
| [19] |
Chang K Y, Chen C S, Hung Y P. Ordinal hyperplanes ranker with cost sensitivities for age estimation[C]//CVPR 2011. June 20-25, 2011, Colorado Springs, CO, USA. IEEE, 2011: 585-592. DOI: 10.1109/CVPR.2011.5995437.
|
 2022, Vol. 39
2022, Vol. 39 


