An ordinary differential equation system is called a Poisson system[1], if it can be written in the following form
| $ \mathrm{d} \boldsymbol{y}(t)=\boldsymbol{B}(\boldsymbol{y}(t)) \nabla H(\boldsymbol{y}(t)) \mathrm{d} t $ | (1) |
where
| $\sum\limits_{l=1}^n\left(\frac{\partial b_{i j}(\boldsymbol{y})}{\partial y_l} b_{l k}(\boldsymbol{y})+\frac{\partial b_{j k}(\boldsymbol{y})}{\partial y_l} b_{l i}(\boldsymbol{y})+\frac{\partial b_{k i}(\boldsymbol{y})}{\partial y_l} b_{l j}(\boldsymbol{y})\right)=0 $ |
for all i, j, k=1, …, n, and H is a smooth function. A function
The Lotka-Volterra (L-V) model of systems with n interacting components is given by
| $ \dot{y}_i=y_i\left(b_i+\sum\limits_{j=1}^n a_{i j} y_j\right), \quad i=1, 2, \cdots, n, $ | (2) |
where aij, bi(i, j=1, 2, …, n) are real parameters. In Ref. [2], the Poisson structure of a class of Lotka-Volterra systems was analyzed, which can be written in the form of (1) with
| $ \begin{aligned} &H(\boldsymbol{y})=\sum\limits_{i=1}^n \beta_i y_i-p_i \ln y_i, \\ &\boldsymbol{B}(\boldsymbol{y})=\left(b_{i j} y_i y_j\right)_{n \times n}= \\ &\operatorname{diag}\left(y_1, \cdots, y_n\right) \boldsymbol{B} \operatorname{diag}\left(y_1, \cdots, y_n\right), \end{aligned} $ | (3) |
where
As is well known, however, stochastic perturbations are unavoidable and universal in real world. Accordingly, there have been literature exploring the Lotka-Volterra system (2) under Gaussian white noise perturbations, which were written in stochastic differential equations (SDEs) of Itô form[3-6]. For instance, Mao et al.[4] showed that the environmental noise suppresses the explosion in the Lotka-Volterra system, i.e., with probability 1 the solution of the stochastic L-V system exists (no explosion in finite time) uniquely under certain non-global Lipschitz conditions; Rudnicki and Pichór[6] analyzed the influence of various stochastic perturbations on prey-predator systems. To the best of our knowledge, however, there is few research on Lotka-Volterra systems under stochastic perturbations of Stratonovich sense, except for the work by Khasminskii and Klebaner[7], which investigated the long term behavior of the solution of the Lotka-Volterra systems under small random perturbations of Stratonovich sense on the birth and death rate.
Poisson systems under certain Stratonovich white noises perturbations, namely the stochastic Poisson systems, got attention in recent years, see e.g. Refs. [8-11], where in Ref. [9], the general form of stochastic Poisson systems was given as
| $ \begin{gathered} \mathrm{d} \boldsymbol{y}(t)=\boldsymbol{B}(\boldsymbol{y}(t))\left(\nabla H_0(\boldsymbol{y}(t)) \mathrm{d} t+\right. \\ \left.\sum\limits_{r=1}^m \nabla H_r(\boldsymbol{y}(t)) \circ \mathrm{d} W_r(t)\right), \end{gathered} $ | (4) |
where
In this paper we consider the Lotka-Volterra systems (1) with (3) under Stratonovich white noise perturbation, of the following form:
| $ \mathrm{d} \boldsymbol{y}(t)=\boldsymbol{B}(\boldsymbol{y}(t)) \nabla H(\boldsymbol{y}(t))(\mathrm{d} t+c \circ \mathrm{d} W(t)), $ | (5) |
where c>0 denotes the intensity of random noise, and W(t) is a one-dimensional standard Wiener process. Obviously it is a stochastic Poisson system according to (4). The stochastic version of the Lotka-Volterra system studied as an example in Ref. [8] is of this form. However, it can be seen that the coefficients of the system do not satisfy the global Lipschitz and linear growth conditions guaranteeing existence and uniqueness of the solution[12-13]. When transfered into its equivalent Itô form, the drift coefficient is cubic, which is different from the equations with non-global Lipschitz and non-linearly growing coefficients considered in the Refs. [3-7], wherefore the results regarding well-posedness of the solutions in these literature are not applicable for this system either. It then arises the question, whether the system (5) with (3) has a unique solution, which does not explode in a finite time, with probability 1. Moreover, the definiton of
We first introduce some notations. To write a vector
It is not difficult to verify that
| $ C(\boldsymbol{y})=\alpha_1 \ln y_1+\cdots+\alpha_n \ln y_n $ |
for
Proposition 1.1 Let
Proof By the Stratonovich chain rule, it holds on [0, T]:
| $ \begin{aligned} &\mathrm{d} H(\boldsymbol{y}(t))=\nabla H(\boldsymbol{y}(t))^{\mathrm{T}} \circ \mathrm{d} \boldsymbol{y}(t) \\ &=\nabla H(\boldsymbol{y}(t))^{\mathrm{T}} \boldsymbol{B}(\boldsymbol{y}(t)) \nabla H(\boldsymbol{y}(t)) \\ &(\mathrm{d} t+c \circ \mathrm{d} W(t))=0 \\ & \end{aligned} $ |
where the last equality is due to skew-symmetry of
| $ \begin{aligned} &\mathrm{d} C(\boldsymbol{y}(t)) \\ &=\nabla C(\boldsymbol{y}(t))^{\mathrm{T}} \circ \mathrm{d} \boldsymbol{y}(t) \\ &=\nabla C(\boldsymbol{y}(t))^{\mathrm{T}} \boldsymbol{B}(\boldsymbol{y}(t)) \nabla H(\boldsymbol{y}(t))(\mathrm{d} t+c \circ \mathrm{d} W(t)) \\ &=0 . \end{aligned} $ |
Thus
| $ \begin{aligned} &\mathrm{d} f(H(\boldsymbol{y}(t)), C(\boldsymbol{y}(t)))= \\ &\partial_1 f(H(\boldsymbol{y}), C(\boldsymbol{y})) \circ \mathrm{d} H(\boldsymbol{y}(t))+\partial_2 f(H(\boldsymbol{y}) \\ &C(\boldsymbol{y})) \circ \mathrm{d} C(\boldsymbol{y}(t))=0 . \end{aligned} $ |
In the following, we will prove that the solution of the system (5) with (3) is globally non-explosive and positive almost surely. To this end, we make the following assumptions.
Hypothesis 2.1 Assume that for the parameters
| $ \left\{\begin{array}{l} s \boldsymbol{\beta}>0, \\ -s \boldsymbol{p}+\boldsymbol{\alpha} <0 . \end{array}\right. $ |
Theorem 2.1 Under Hypothesis 2.1, for any given initial value
Proof The equivalent It form of the system (5) with (3) is
| $ \begin{aligned} &\mathrm{d} \boldsymbol{y}(t)=\boldsymbol{B}(\boldsymbol{y}) \nabla H(\boldsymbol{y})(\mathrm{d} t+c \mathrm{~d} W(t))+ \\ &\frac{c^2}{2} \frac{\partial}{\partial \boldsymbol{y}}(\boldsymbol{B}(\boldsymbol{y}) \nabla H(\boldsymbol{y})) \boldsymbol{B}(\boldsymbol{y}) \nabla H(\boldsymbol{y}) \mathrm{d} t . \end{aligned} $ | (6) |
Taking the concrete expressions of
| $ \begin{gathered} \tau_k:=\inf \left\{t \in\left[0, \tau_e\right): y_i(t) \notin(1 / k, k)\right. \\ \text { for some } i=1, \cdots, n\} \end{gathered} $ |
on the probability space
Clearly,
If this statement is not true, then there exist real numbers T>0 and ε∈(0, 1) such that
| $ P\left(\left\{\tau_{\infty} \leqslant T\right\}\right)>\varepsilon, $ |
which implies
| $ P\left(\left\{\tau_k \leqslant T\right\}\right)>\varepsilon \text { for all } k \geqslant k_0, $ |
since
| $ \begin{gathered} \left(a_1, a_2, \cdots, a_n\right):=s \boldsymbol{\beta}>0, \\ \left(d_1, d_2, \cdots, d_n\right):=-s \boldsymbol{p}+\boldsymbol{\alpha} <0 . \end{gathered} $ |
Now, for y>0 we construct the function
| $\begin{aligned} &G(\boldsymbol{y}):=\sum\limits_{j=1}^n a_j y_j+d_j \ln y_j+d_j-d_j \ln \left(-\frac{d_j}{a_j}\right), \\ &G_j\left(y_j\right):=a_j y_j+d_j \ln y_j+d_j-d_j \ln \left(-\frac{d_j}{a_j}\right), \\ &j=1, \cdots, n . \end{aligned} $ | (7) |
We see that
| $ \begin{aligned} G\left(\boldsymbol{y}\left(\tau_k\right)\right) &=\sum\limits_{j=1}^n G_j\left(y_j\left(\tau_k\right)\right) \geqslant \\ G_i\left(y_i\left(\tau_k\right)\right) & \geqslant G_i(1 / k) \wedge G_i(k), \end{aligned} $ |
where
| $ \begin{gathered} G(\boldsymbol{y}(t)) \equiv s H(\boldsymbol{y}(t))+C(\boldsymbol{y}(t))+ \\ \sum\limits_{j=1}^n\left(d_j-d_j \ln \left(-\frac{d_j}{a_j}\right)\right) \end{gathered} $ |
is an invarint of the system on the time interval [0, τk∧T]. Then set
| $ \begin{aligned} G(\boldsymbol{y}(0))=& E\left[G\left(\boldsymbol{y}\left(\tau_k \wedge T\right)\right)\right] \\ & \geqslant E\left[1_{\varOmega_{\mathrm{k}}} \mathrm{G}\left(\boldsymbol{y}\left(\tau_k \wedge T\right)\right)\right] \\ &=E\left[1_{\varOmega_{\mathrm{k}}} \mathrm{G}\left(\boldsymbol{y}\left(\tau_k\right)\right)\right] \\ &>\varepsilon\left[G_i(1 / k) \wedge G_i(k)\right] . \end{aligned} $ |
Let k→∞ in the above inequality, we then draw the contradiction
| $ G(\boldsymbol{y}(0))>+\infty . $ |
Thus it holds τ∞=+∞ almost surely.
Remark 2.1 When the constant matrix
Remark 2.2 Under Hypothesis 2.1, the solution y(t) is positive on [0, +∞) almost surely, then f(H(y(t)), C(y(t))) given in Proposition 1.1 is a class of invariants of the system (5)with (3) on [0, +∞).
3 Boundedness of the positive solutionBased on Theorem 2.1, we can further obtain the boundedness of the positive solution y(t).
Proposition 3.1 Under Hypothesis 2.1, for any given initial value
Proof According to Remark 2.2, almost surely, the constructed function
| $ \begin{aligned} G(\boldsymbol{y}(t))=& \sum\limits_{j=1}^n a_j y_j(t)+d_j \ln \left(y_j(t)\right)+\\ & d_j-d_j \ln \left(-\frac{d_j}{a_j}\right) \end{aligned} $ |
in (7) is an invariant of the system (5) with (3) on [0, +∞), i.e., G(y(t))≡G(y(0)). Moreover, the function Gj(yj) has the minimum value
| $ \begin{gathered} G_i\left(y_i(t)\right)=G(\boldsymbol{y}(0))- \\ \sum\limits_{j \neq i}^n G_j\left(y_j(t)\right) \leqslant G(\boldsymbol{y}(0)), \text { i. e. }, \\ a_i y_i(t)+d_i \ln \left(y_i(t)\right)+d_i- \\ d_i \ln \left(-\frac{d_j}{a_j}\right) \leqslant G(\boldsymbol{y}(0)) . \end{gathered} $ |
Hence,
| $z=\frac{a_i}{2}\left(y_i+\frac{2 d_i}{a_i}\right)+G_i\left(-\frac{2 d_i}{a_i}\right) . $ |
Then by the convexity of
| $ \begin{gathered} \frac{a_i}{2}\left(y_i(t)+\frac{2 d_i}{a_i}\right)+G_i\left(-\frac{2 d_i}{a_i}\right) \leqslant \\ G_i\left(y_i(t)\right) \leqslant G(\boldsymbol{y}(0)), \end{gathered} $ |
which implies
| $ 0 <y_i(t) \leqslant \frac{2\left[G(\boldsymbol{y}(0))-d_i \ln 2\right]}{a_i} $ |
for all t≥0 and i=1, …, n.
4 Numerical validationsIn this section, we simulate the solutions of two concrete models of the form (5) with (3), by the numerical method proposed in Ref. [8] for stochastic Poisson systems of the form (5), which was proved to be of root mean-square convergence order 1, and reads
| $ \begin{aligned} &y_{n+1}=y_n+\boldsymbol{B}\left(\frac{y_n+y_{n+1}}{2}\right) \\ &\int_0^1 \nabla H\left(y_n+\tau\left(y_{n+1}-y_n\right)\right) \mathrm{d} \tau\left(h+c \Delta \hat{W}_n\right) \end{aligned} $ | (8) |
where h is the time step,
| $ \zeta_h= \begin{cases}\xi, & \text { if } \quad \xi \leqslant\left|A_h\right|, \\ A_h, & \text { if } \quad \xi>A_h, \\ -A_h, & \text { if } \quad \xi <-A_h, \end{cases} $ |
where
Consider the three-dimensional Lotka-Volterra system with Stratonovich white noise perturbation[8]
| $ \begin{gathered} \mathrm{d} \boldsymbol{y}(t)=\boldsymbol{B}(\boldsymbol{y}(t)) \nabla H(\boldsymbol{y}(t))(\mathrm{d} t+c \circ \mathrm{d} W(t)), \\ \boldsymbol{B}(\boldsymbol{y})=\left(\begin{array}{ccc} 0 & v y_1 y_2 & b v y_1 y_3 \\ -v y_1 y_2 & 0 & -y_2 y_3 \\ -b v y_1 y_3 & y_2 y_3 & 0 \end{array}\right), \\ H(y)=a b y_1+y_2+\gamma \ln y_2-a y_3-\mu \ln y_3 . \end{gathered} $ | (9) |
By simple calculation one can varify that
First set
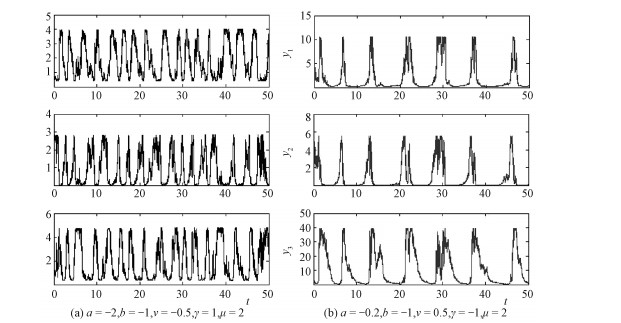
|
Download:
|
|
Fig. 1 Sample paths of the system (9) |
|
Then we set another group of parameters
In Fig. 1, we take the parameter
We consider a prey-predator model[1] with random pertubation
| $ \left(\begin{array}{l} \mathrm{d} u \\ \mathrm{~d} v \end{array}\right)=\left(\begin{array}{l} u(v-2) \\ v(1-u) \end{array}\right)(\mathrm{d} t+c \circ \mathrm{d} W(t))= \\ \left(\begin{array}{cc} 0 & u v \\ -u v & 0 \end{array}\right) \nabla H(u, v)(\mathrm{d} t+c \circ \mathrm{d} W(t)), $ | (10) |
where
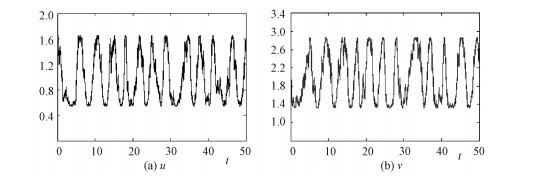
|
Download:
|
|
Fig. 2 Sample paths of the system (10) |
|
Here we take c=0.5, and the initial value (u(0), v(0))=(1.5, 2.5), the step size h=10-3.
5 ConclusionWe prove the almost sure existence (global non-explosion), uniqueness and positiveness of the solution of a class of stochastic Poisson systems, under certain hypothesis, via constructing a function G(y) which is a special class of invariants of the systems. Almost sure boundedness of the solution is also verified. Numerical simulations give support to the theoretical results.
| [1] |
Hairer E, Lubich C, Wanner G. Geometric numerical integration: structure-preserving algorithms for ordinary differential equations[M]. 2nd ed. Berlin: Springer Berlin Heidelberg, 2002: 256-257.
|
| [2] |
Plank M. Hamiltonian structures for the n-dimensional Lotka-Volterra equations[J]. Journal of Mathematical Physics, 1995, 36(7): 3520-3534. DOI:10.1063/1.530978 |
| [3] |
Arnold L, Horsthemke W, Stucki J W. The influence of external real and white noise on the Lotka-Volterra model[J]. Biometrical Journal, 1979, 21(5): 451-471. DOI:10.1002/bimj.4710210507 |
| [4] |
Mao X R, Marion G, Renshaw E. Environmental Brownian noise suppresses explosions in population dynamics[J]. Stochastic Processes and Their Applications, 2002, 97(1): 95-110. DOI:10.1016/S0304-4149(01)00126-0 |
| [5] |
Mao X R, Sabanis S, Renshaw E. Asymptotic behavior of the stochastic Lotka-Volterra model[J]. Journal of Mathematical Analysis and Applications, 2003, 287(1): 141-156. DOI:10.1016/S0022-247X(03)00539-0 |
| [6] |
Rudnicki R, Pichór K. Influence of stochastic perturbation on prey-predator systems[J]. Mathematical Biosciences, 2007, 206(1): 108-119. DOI:10.1016/j.mbs.2006.03.006 |
| [7] |
Khasminskii R Z, Klebaner F C. Long term behavior of solutions of the Lotka-Volterra system under small random perturbations[J]. The Annals of Applied Probability, 2001, 11(3): 952-963. DOI:10.1214/aoap/1015345354 |
| [8] |
Cohen D, Dujardin G. Energy-preserving integrators for stochastic Poisson systems[J]. Communications in Mathematical Sciences, 2014, 12(8): 1523-1539. DOI:10.4310/cms.2014.v12.n8.a7 |
| [9] |
Hong J L, Ruan J L, Sun L Y, et al. Structure-preserving numerical methods for stochastic Poisson systems[J]. Communications in Computational Physics, 2021, 29(3): 802-830. DOI:10.4208/cicp.oa-2019-0084 |
| [10] |
Li X Y, Ma Q, Ding X H. High-order energy-preserving methods for stochastic Poisson systems[J]. East Asian Journal on Applied Mathematics, 2019, 9(3): 465-484. DOI:10.4208/eajam.290518.310718 |
| [11] |
Wang P J, Wang L J. Stochastic Poisson integrators based on Padé approximations for linear stochastic Poisson systems[J]. Journal of University of Chinese Academy of Sciences, 2021, 38(2): 160-170. DOI:10.7523/j.issn.2095-6134.2021.02.002 |
| [12] |
Arnold L. Stochastic differential equations: theory and applications[M]. New York: Wiley, 1974: 112-113.
|
| [13] |
Mao X R. Stochastic differential equations and applications[M]. 2nd ed. Cambridge: Woodhead Publishing, 2007: 56-58.
|
 2022, Vol. 39
2022, Vol. 39 


