在经典的板块构造理论中,岩石圈板块是刚性的,板块在地球表面的运动可近似看作是刚体的定点转动,由角速度向量(Euler vector)描述[1]。描述板块运动的模型分为板块相对运动模型和板块绝对运动模型。板块相对运动模型基于地球物理和空间大地测量数据(包括地震滑移矢量、洋中脊扩张速率、转换断层方位角及GPS等空间观测的结果),确定板块的划分并得到板块之间相对运动的角速度[2-6]。板块绝对运动模型研究板块相对于深部地幔的运动。前人研究中常用的代表深部地幔的参考系包括热点参考系[7-9]和无合转动(no-net-rotation)参考系[5, 10]。由于板块边界受力的不对称及软流圈黏度的不均匀性,岩石圈可能存在整体的合转动[11-13],基于热点参考系的板块绝对运动模型更符合板块动力学研究的需要。本文基于相对起源于深部地幔柱的热点定义的板块绝对运动模型T25M[13]研究板块运动的驱动力。
前人关于刚性板块运动的研究通常以下列两个基本假设为前提:一是板块运动的角速度在至少几百万年内是保持恒定的,可以给出一套板块的角速度向量描述相当长时间内各板块的运动[4];二是各板块处于力矩平衡状态,可以用板块力矩平衡拟合得出板块受到的各种力矩的相对大小[14]。事实上,以上两个假设并不等价。当刚体旋转轴不沿其惯量主轴时,其角速度与角动量方向存在夹角,由刚性板块的力矩平衡可以导出其角动量恒定,但不能同时保证角速度恒定。本文将对这一问题作深入分析。
对于板块运动的驱动力,早期的研究认为地幔对流推动着板块运动,就像在传送带上运送物品一样[15]。然而,考虑到岩石圈作为边界层成为地幔对流系统的一部分时,板块底面的剪切力总体上起着黏滞板块运动的阻力作用[16-17]。后续大量研究工作将岩石圈处理为独立的子系统,研究该子系统中的各种作用力[18-19],主要包括:与俯冲板片有关的力、洋中脊推力、板底拖曳力和碰撞带产生的力等。
有关板块运动的驱动机制,现有的研究主要从以下两方面开展:第1类研究从板块力矩平衡出发,设定一些力矩的参数,拟合求解各种力矩在力矩平衡条件下的取值[14, 18-21]。在计算板块受到的力矩时,通常以地心作为矩心(支点),其优势是可以近似认为板块受到的重力指向地心而软流圈对板块的支持力背离地心,这两种力的力臂为零,从而简化力矩平衡的计算过程。这类研究的主要结论是:俯冲板片负浮力与板片所受阻力比其他作用力约大一个数量级,但俯冲板片上的合力与其他驱动力量级相当;地幔对岩石圈底部的剪切力阻碍板块运动,且大陆板块板底剪切力比大洋板块更大。由于问题的超定性,虽然不同作者假设的驱动力模式设定有所不同,但均能为各板块建立较好的力矩平衡[22]。第2类研究直接根据板块边界形状计算板块所受驱动力矩,比较驱动力矩与板块绝对运动角速度的方向[23-24]。由角动量定理可知,力矩与角动量而不是角速度之间存在相关性,将驱动力矩与板块角速度直接对比缺乏足够的物理基础。
在计算板块边界力矩方面,源于大洋板块地形的洋脊推力的计算方法较为成熟,而由于俯冲板片所受地幔阻力不易计算,俯冲板片净拉力的计算存在困难[25]。在计算板底剪切力矩方面,前人普遍采用均匀拖曳系数的方法[14, 18-19],仅能考虑大陆和大洋下软流圈的黏度差异。
本文采用板块驱动上地幔流动的模型,并利用由上地幔物理条件约束的地幔黏度分布[25],计算上地幔物质的剪切流动状态,进而计算作用于各板块的板底剪切力及其力矩。结合洋脊推力矩的定量计算结果,研究现今岩石圈板块的力矩平衡关系,进而对板底剪切和洋脊推力以外的板块作用力进行讨论。
1 板块运动稳定性分析考虑板块运动为刚体的定点转动,角动量定理要求板块所受合外力矩T等于角动量L对时间的导数
| $ \boldsymbol{T}=\frac{\mathrm{d} \boldsymbol{L}}{\mathrm{d} t}, $ | (1) |
其中角动量L定义为转动惯量I与角速度ω的乘积
| $ \boldsymbol{L}=\boldsymbol{I} \boldsymbol{\omega} . $ | (2) |
刚体的转动惯量I是一个二阶张量,在直角坐标系中可以按以下形式积分计算
| $ \begin{aligned} &\boldsymbol{I}= \\ &{\left[\begin{array}{ccc} \int \rho\left(y^{2}+z^{2}\right) \mathrm{d} V & -\int \rho x y \mathrm{d} V & -\int \rho x z \mathrm{d} V \\ -\int \rho x y \mathrm{d} V & \int \rho\left(x^{2}+z^{2}\right) \mathrm{d} V & -\int \rho y z \mathrm{d} V \\ -\int \rho x z \mathrm{d} V & -\int \rho y z \mathrm{d} V & \int \rho\left(y^{2}+x^{2}\right) \mathrm{d} V \end{array}\right] .} \end{aligned} $ | (3) |
如果建立在固结于刚体惯量主轴的坐标系,其中的刚体转动动力学欧拉方程可以写为以下形式
| $ \begin{aligned} &I_{x x} \dot{\omega}_{x}-\left(I_{y y}-I_{z z}\right) \omega_{y} \omega_{z}=T_{x}, \\ &I_{y y} \dot{\omega}_{y}-\left(I_{z z}-I_{x x}\right) \omega_{x} \omega_{z}=T_{y}, \\ &I_{z z} \dot{\omega}_{z}-\left(I_{x x}-I_{y y}\right) \omega_{x} \omega_{y}=T_{z}, \end{aligned} $ | (4) |
其中: Ixx、Iyy、Izz为3个方向的主惯量,ωx、ωy、ωz为3方向角速度分量,Tx、Ty、Tz为3方向合力矩分量[26]。
如果板块受到方向与运动速度相反的板底阻力约束,考虑简单的板块驱动上地幔层流,板底阻力矩Tpb为
| $ \boldsymbol{T}_{p b}=-\boldsymbol{r} \times \mu A \frac{\boldsymbol{\omega} \times \boldsymbol{r}}{h_{\mathrm{um}}}=-\mu r^{2} A \frac{\boldsymbol{\omega}}{h_{\mathrm{um}}}, $ | (5) |
其中: r为地球半径矢量,μ为上地幔黏度,A为板块底面积,hum为上地幔厚度。
对于均匀密度ρ、厚度hlp的岩石圈板块,其主惯量为
| $ I=\rho r^{2} A h_{\mathrm{lp}}, $ | (6) |
结合式(2)、式(5)和式(6)可以得到
| $ \boldsymbol{T}_{p b}=-\frac{\mu}{\rho h_{\mathrm{lp}} h_{\mathrm{um}}} \boldsymbol{L} . $ | (7) |
式(7)表明,板底阻力矩与板块角动量方向相反,大小成正比,比例系数为
| $ c=\frac{\mu}{\rho h_{\mathrm{lp}} h_{\mathrm{um}}}, $ | (8) |
取上地幔黏度μ量级1021 Pa·s、岩石圈密度ρ量级3×103 kg/m3、岩石圈厚度hlp量级100 km和上地幔厚度hum量级600 km的典型值计算[25],比例系数c量级为106/s。
带有板底力矩的欧拉方程如下
| $ \begin{aligned} &I_{x x} \dot{\omega}_{x}-\left(I_{y y}-I_{z z}\right) \omega_{y} \omega_{z}=T_{x}-\omega_{x} c I_{x x}, \\ &I_{y y} \dot{\omega}_{y}-\left(I_{z z}-I_{x x}\right) \omega_{x} \omega_{z}=T_{y}-\omega_{y} c I_{y y}, \\ &I_{z z} \dot{\omega}_{z}-\left(I_{x x}-I_{y y}\right) \omega_{x} \omega_{y}=T_{z}-\omega_{z} c I_{z z}, \end{aligned} $ | (9) |
这里Tx、Ty、Tz代表除板底力矩以外的合力矩分量。由数量级估计,板块转动惯量数量级为1035 kg·m2,角速度数量级为10-16 rad/s,所受力矩数量级为1025 N·m。由此,欧拉方程中第2项远小于其他项,可以忽略。方程(9)近似为
| $ \begin{aligned} &I_{x x} \dot{\omega}_{x}=T_{x}-\omega_{x} c I_{x x}, \\ &I_{y y} \dot{\omega}_{y}=T_{y}-\omega_{y} c I_{y y}, \\ &I_{z z} \dot{\omega}_{z}=T_{z}-\omega_{z} c I_{z z}, \end{aligned} $ | (10) |
解得
| $ \begin{aligned} &\omega_{x}=\frac{T_{x}}{c I_{x x}}+\left(\omega_{x 0}-\frac{T_{x}}{c I_{x x}}\right) \mathrm{e}^{-c t}, \\ &\omega_{y}=\frac{T_{y}}{c I_{y y}}+\left(\omega_{y 0}-\frac{T_{y}}{c I_{y y}}\right) \mathrm{e}^{-c t}, \\ &\omega_{z}=\frac{T_{z}}{c I_{z z}}+\left(\omega_{z 0}-\frac{T_{z}}{c I_{z z}}\right) \mathrm{e}^{-c t}, \end{aligned} $ | (11) |
其中:ωx0、ωy0、ωz0为初始角速度的3个分量。式(11)解中右侧第2项在10-6秒量级时间内迅速衰减,即由于板底剪切力矩对于板块运动的约束非常强大,对于板块边界上施加力矩的变化,板块角速度的响应十分迅速,能在很短的时间内达到新的平衡。
如果认为一般情况下,板块处于力矩平衡状态,其角动量保持恒定,板底阻力矩近似与板块角动量方向相反,则其他力矩的合力矩与角动量方向近似相同。这种板块角动量方向与驱动力矩之间的内在联系并不存在于角速度方向与驱动力矩之间。由于板块在运动过程中转动惯量可以不断变化,引起其角速度与角动量间夹角的变化,角速度方向与驱动力矩间没有简单的依赖关系。因此,不同于Richardson[24]比较力矩与角速度方向的方法,本文提出更符合物理规律的比较板块角动量与板块受到的各类力矩以识别驱动力的方法:驱动板块运动的力矩方向应接近板块角动量的方向,而阻碍板块运动的力矩则大致与角动量方向相反。这样可以有效识别板块运动的驱动力与阻力。
2 板块角动量计算计算板块的角动量需已知岩石圈板块的几何划分、密度分布和运动状态。NNR-MORVEL56模型[10]给出了全球56个板块的边界划分,这一模型在PB2002模型[27]的基础上新增4条板块边界,PB2002模型给出了全球各条板块边界的类型。最新的基于深部地幔柱参考系的板块绝对运动模型T25 M[13]给出了56个板块绝对运动的角速度向量。Litho1.0岩石圈结构模型[28]给出了全球岩石圈的三维结构信息,该模型将地球表面划分为40 962个点组成的81 920个三角形的网格,给出了每个坐标点下岩石圈的深度分层与密度信息。为简化运算,本文将模型中岩石圈的9层划分简化为4层并对每一层的密度取一个确定值(图 1)。

|
Download:
|
| 图 1 本文简化后的Litho1.0模型[28]分层示意 Fig. 1 Schematics of the Litho 1.0 model[28] simplified in this paper | |
选取全球面积最大的19个板块作为研究对象(占地球表面积的97%),通过寻找每个板块内的Litho1.0模型网格,将其质量分布做式(3)中的积分,得到每个板块的转动惯量张量,用惯量张量乘以T25 M模型给出的板块角速度可以得到板块角动量向量。计算得到的各板块的角动量向量见表 1。
|
|
表 1 板块角动量 Table 1 Angular momentum of the plates |
洋脊推力由洋底地形与大洋岩石圈的密度结构决定。Turcotte和Schubert[25]得出,洋脊推力随大洋岩石圈年龄成正比地增大,直到年龄100 Ma的大洋板块洋脊推力达到约为4×1012 N/m的典型值后,更老的洋底基本不再继续下沉。本文结合大洋岩石圈年龄分布[29]对老于100 Ma的大洋板块均设定洋脊推力为4×1012 N/m,而对较为年轻的大洋板块根据其年龄做比例调整,计算得到洋脊推力(图 2)。采用MORVEL56模型板块边界类型的划分,以地球半径作为力臂,对每一段洋脊的推力求得力矩,对这些力矩求和可以得到一个板块受到的洋脊合力矩。

|
Download:
|
| 红色边界为洋中脊,蓝色边界为俯冲带,板块简称参照 MORVEL56 模型[10] 图 2 洋脊推力与俯冲板片负浮力(单位1012 N/m)的全球分布 Fig. 2 The global distribution of the ridge push and slab pull forces measured in 1012 N/m | |
俯冲板片因其热结构受到负浮力,因俯冲运动受到周围地幔物质的流体压力,表现为板片下方的托力和上方的吸力[30-31]。负浮力垂直于板片的分量与板片下方地幔的托力和上方地幔的吸力平衡,维持了俯冲角度[32]。负浮力沿板片分量与周围地幔对板片阻力的合力作为板片净拉力作用在板块上[33-34]。板片负浮力比洋脊推力大一个量级,但板片受到周围地幔阻力与地幔流动和黏度状态相关,使得俯冲板片的净拉力可能与洋脊推力量级相同[25]。Schellart[34]通过沙箱实验方法得到俯冲板片净拉力大约是负浮力的8%~12%。俯冲板片负浮力沿板片方向分量的大小可以由以下公式[14]计算:
| $ F_{\mathrm{sp}}=\Delta \rho g L H \sin \theta, $ | (12) |
其中: Δρ为俯冲板片与周围地幔物质的密度差,McNutt[35]给出的参考值为80 kg/m3,g为重力加速度, L为俯冲板片长度,H为俯冲板片厚度,θ为俯冲倾角。考虑岩石圈冷却模型,H可由以下公式[25]计算:
| $ H=2.32 \sqrt{\kappa t}, $ | (13) |
其中: 热扩散系数κ取值1 mm2/s, t为俯冲处的板块年龄。Lallemand等[36]整理了全球俯冲带上159个地点的俯冲板片的各项参数,包含板片俯冲处的大洋岩石圈年龄、板片长度和俯冲倾角。由其文中的参数和上述公式可以计算俯冲板片负浮力沿板片方向的分量,本文假设该力在俯冲板片弯折处直接传递作为对板块的水平拉力。将159个点的取值在同一条板块俯冲边界上做平均处理,得到全球各条俯冲边界上单位长度负浮力对板块水平拉力的大小(图 2)。以地球半径为力臂,估算出各板块的负浮力力矩。
为简化计算,假设全球所有转换断层边界上不受力,大陆裂谷受到1012 N/m的扩张力,碰撞带边界受到1012 N/m的挤压力。以地球半径为力臂计算裂谷和碰撞带上的力矩,这两种力矩的大小只作为数量级上的参考。
3.2 板底剪切力矩计算定义板底剪切力为板块运动的阻力,其方向与当地的板底速度方向相反。由牛顿黏滞定律,对于板底面积元Ai,其板底力如下
| $ \boldsymbol{F}_{i}=-\mu A_{i} \frac{\mathrm{d} u_{i}}{\mathrm{~d} h_{i}}, $ | (14) |
其中:μ是上地幔黏度,
应用干上地幔(dry upper mantle)位错蠕变下的黏度随温度、压力变化的计算公式[25, 37]:
| $ \mu=C_{2}\left(\frac{G}{\tau}\right)^{2.5} \mathrm{e}^{\frac{E_{a}+p V_{a}}{R T}}, $ | (15) |
其中:C2=1.14×10-12 Pa·s,G=8×1010 Pa,τ=μ
| $ a T_{m}=\frac{E_{a}+p V_{a}}{R}, $ | (16) |
上地幔黏度可以表达为
| $ \mu=C_{2}\left(\frac{G}{\tau}\right)^{2.5} \mathrm{e}^{\frac{a T_{\mathrm{m}}}{T}}, $ | (17) |
其中: a为上地幔物质的活化能Ea、地表的熔点Tm0和普适气体常数R决定的常数,取值为29.4,Tm是上地幔物质的熔点。
对于上地幔温度分布,设定660 km深度温度为1 875 K,上地幔温度梯度为绝热温度梯度[25]:
| $ \frac{\mathrm{d} T}{\mathrm{~d} h}=\frac{\alpha_{v} g T}{c_{p}}, $ | (18) |
其中: αv=3×10-5 K-1,cp=1 000 J·kg-1·K-1,g=9.8 m·s-2,可以得到温度T(K)与深度h(km)的关系
| $ T=1\ 544.3 \mathrm{e}^{2.94 \times 10^{-4} h}. $ | (19) |
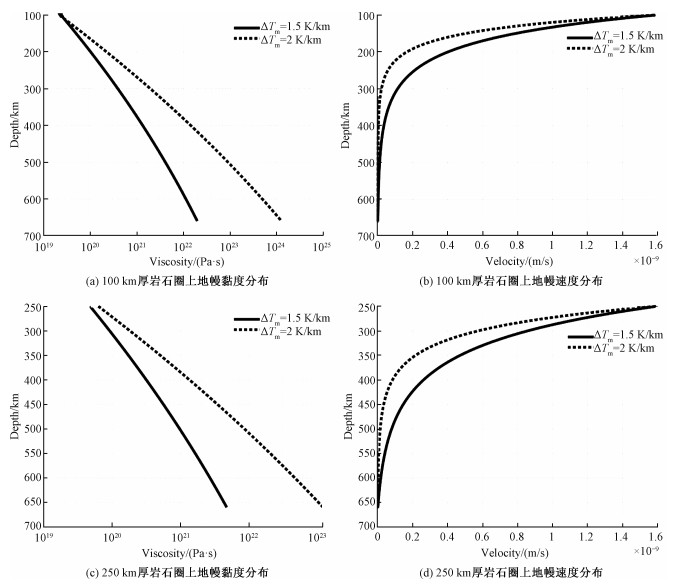
对于上地幔物质的熔点Tm,Turcotte和Schubert[25]给出的参考值为地表Tm0=2 140 K,Tm随深度增加的合理梯度为2 K/km,这个梯度取值较大。采用Tm取2 K/km和1.5 K/km两个深度梯度,分别对于一个厚度为100 km和250 km的岩石圈板块,令其运动速度u=1.6×10-9 m/s (5 cm/a), 由式(17)的黏度分布计算板底剪应力与上地幔物质流速分布,如图 3所示。
|
Download:
|
| 图 3 对应于两种熔点梯度取值的上地幔黏度和速度分布 Fig. 3 Viscosity and velocity distributions of the upper mantle corresponding to two melting point gradients | |
由图 3可以看出,Tm梯度取2 K/km时得到的上地幔黏度较大,在660 km深超过了1023 Pa·s量级,使得地幔流动只在浅部发生,其计算出的板底剪应力较大。因此,取Tm梯度为1.5 K/km,即
| $ T_{\mathrm{m}}=2\ 140+1.5 {~h}. $ | (20) |
至此,可以采用式(17)计算全球各地的板底剪应力和各板块的板底剪切阻力矩。
将计算的全球各地板底剪应力作分布图,与Litho1.0模型给出的LAB界面深度分布图对比,如图 4所示。

|
Download:
|
| 图 4 全球LAB深度[28]与板底剪应力分布对比 Fig. 4 Comparison between the global distributions of LAB depths[28] and basal shear stresses | |
对比图 4可以看出,对于同一个板块,板底剪应力大小与岩石圈厚度呈高度正相关。同时,板底剪应力大小也与板块运动速度呈正相关。AU、CP、IN、PS、PA、NZ、CO等板块运动速度大,在岩石圈厚度相同的区域板底剪应力整体大于其余板块。
3.3 作用于板块的力矩与驱动力识别依据前文所述方法分别计算了每个板块受到的洋脊、板片负浮力、裂谷、碰撞、板底剪切5种力矩,表 2列出了9个板块所受主要力矩的计算结果。
|
|
表 2 作用于板块的各种力矩 Table 2 Various types of torques acting on the plates |
5种力矩中,洋脊力矩和板底力矩的计算过程有较好的物理模型作为约束,其计算结果较为可靠,而负浮力力矩计算结果应当比板片净拉力矩大一个量级且约束较差。裂谷力矩和碰撞力矩大小的计算结果只具有数量级上的参考价值。
将各种力矩与板块运动的角动量作夹角,结果列于表 3。
|
|
表 3 板块作用力矩与角动量间夹角 Table 3 Angles between various torques and the plate angular momentum |
由表 3可以识别出板块运动的驱动力。表中所列板块的板底力矩与板块角动量的夹角均相当接近于180°,这与前文理论推导得到的板底力矩近似与板块角动量方向相反的结论吻合。总体上,洋脊、负浮力力矩多为驱动力矩,非洲裂谷力矩阻碍了NU板块的运动,碰撞力矩驱动了EU板块的运动。
4 板块运动驱动机制讨论 4.1 与洋脊力矩和板底力矩平衡的剩余力矩考虑板块力矩平衡,以上求得的同一板块各种力矩之和应为零。如果计算与洋脊力矩和板底力矩平衡的剩余力矩,这一剩余力矩应当可以指示俯冲、裂谷、碰撞等力矩的综合作用效果。为方便作图,采用式(21)将力矩化为等效应力
| $ \boldsymbol{\tau}=\frac{\boldsymbol{T} \times \boldsymbol{r}}{r^{2} A}, $ | (21) |
其中:T为力矩,r为地球半径,A为板块面积。图 5选取了板块中的一些代表点,给出了各板块上与洋脊力矩、板底力矩和剩余力矩对应的等效应力分布,并区分了全球板块边界的类型。图中红线是洋中脊,绿线是转换断层,黑线是俯冲带,紫线是碰撞带,橙线是大陆裂谷,棕线是MORVEL56模型新增的4条板块边界。

|
Download:
|
| 图 5 由等效应力表示的各板块洋脊力矩(红色箭头)、板底力矩(绿色箭头)和剩余力矩(蓝色箭头)比较 Fig. 5 Comparison between the ridge, basal and residual torques expressed by the equivalent stresses acting on the plates (The red, green and blue arrows show the ridge, basal and residual torques, respectively) | |
由图 5可见,PA、AU、PS这3个板块剩余力矩的等效应力都指向俯冲边界方向,其剩余力矩与前文计算的负浮力力矩夹角较小,可将剩余力矩归因为俯冲板片产生的拉力矩。剩余力矩的等效应力大小和洋脊力相当,支持了前人俯冲板片上的合力与洋脊力量级相当的观点[18]。
CO、NZ两个板块的剩余力矩的等效应力指向俯冲边界的反向。对此结果的一种解释为前文计算高估了年轻板块洋脊力的大小或者低估了年轻大洋岩石圈板底剪切力的大小;另一种解释为由于东太平洋俯冲带的俯冲形态较平缓[38],存在的碰撞阻力大于俯冲板片拉力,使得俯冲边界上的力沿板块运动方向的反向,阻碍板块运动。
对于NA板块,洋脊力矩与板底力矩几乎平衡,即该板块其他边界上作用力的合效应很小。对于SA板块,剩余力矩可以由西侧的NZ板块俯冲带对上覆板块的碰撞力解释,这一碰撞力的大小约为洋脊力的一半。对于NU板块,剩余力矩的等效应力指向背离裂谷的方向,剩余力矩与前文计算的裂谷力矩方向基本一致,可由略小于洋脊推力的东非裂谷扩张力解释。
对于EU板块,剩余力矩的等效应力指向背离地中海—喜马拉雅碰撞带的方向,剩余力矩与前文计算的碰撞力矩方向基本一致,可由与洋脊推力相当的大陆碰撞带产生的力解释。Warners-Ruckstuhl等[39-40]的研究认为喜马拉雅碰撞带上的力大小为(7.0~10.5)×1012 N/m,中东地区为(1.3~2.7)×1012 N/m。由此,EU板块可由大陆碰撞力驱动。
对于OK、AM板块,其剩余力矩可由西侧的裂谷扩张和碰撞带产生的力解释,这种力可以视为喜马拉雅碰撞带产生的力经过EU板块传递后施加在OK、AM板块上,驱动了板块的运动。
AN板块的运动角速度很小,板底力矩的作用较小,而其四周边界三边为洋脊扩张,在SA、NZ板块南部一边为转换断层边界,其剩余力矩可由转换断层上的碰撞力解释。
4.2 有关古板块角速度突然变化的讨论本文式(11)解可以合理解释地质历史上板块运动的突然转向,即板块边界力矩的变化导致板块角速度变化的过程十分迅速。有关古板块运动方向的转变,可以讨论不平衡过程前后的两个平衡过程。用本文采用的力矩平衡方法,如果已知一个古板块的几何结构和绝对运动角速度,建立当时的板块运动力矩平衡模型,比较板块运动角速度明显变化前后的两个力矩平衡过程[41],可以探究板块角速度变化的原因。参考前人的古板块运动模型重建结果[42-44],对于近50 Ma来全球主要板块运动特征的变化,有3个板块值得讨论:
1) 太平洋板块在大约43 Ma前运动方向有一次转向,这次转向前后的太平洋板块运动由Hawaiian-Emperor岛链的弯折真实地记录下来[45]。对比转向前后的太平洋板块边界可以得出,这次转向可能与西太平洋俯冲带的产生有关。如果建立转向前洋脊驱动力与板底剪切阻力平衡的北向运动模型,和转向后板块由西向俯冲带驱动与板底剪切阻力平衡的西向运动模型[46],可以验证这一猜想。
2) 印度板块在大约40 Ma前由于与欧亚板块的碰撞,运动角速度大幅减小[41]。对比碰撞前后的板块边界可以看出,之前向北俯冲的俯冲边界转变为大陆碰撞带,俯冲拉力转变为碰撞阻力。建立碰撞前的洋中脊和俯冲带驱动,与板底阻力平衡的快速运动模型,和碰撞后的洋中脊和俯冲带驱动,与板底剪切阻力和碰撞阻力平衡的慢速运动模型,可以说明印度板块角速度减慢的原因。
3) 欧亚板块在近40 Ma以来在印度、阿拉伯、地中海地区的相继碰撞下运动速度有一次转向,由之前的东南向运动转变为东北向运动。建立碰撞前的洋脊推力驱动与板底剪切阻力平衡的模型,和碰撞后大陆碰撞力驱动与洋脊推力和板底剪切阻力平衡的模型,可以说明欧亚板块这次转向的原因。
5 结论本文基于板块的力矩平衡研究其动力学问题,提出由力矩与角动量的夹角大小识别板块驱动力的方法,并依据最新的板块绝对运动模型计算了板块转动惯量、角动量、板底剪切阻力及板块边界的主要作用力。基本结论如下:
1) 板底剪切力矩与板块角动量方向大致相反,而板块受到的其他力矩之和则作为驱动力矩近似沿板块角动量方向。
2) 利用板块所受力矩与板块角动量的夹角可以识别板块驱动力矩。总体上,洋脊力矩、板片负浮力力矩多为板块运动驱动力矩。非洲裂谷力矩阻碍NU板块的运动,碰撞力矩驱动EU板块运动。
3) 通过建立合理的物理模型计算洋脊力矩和板底力矩,可以求出与之平衡的剩余力矩。剩余力矩可以指示俯冲、裂谷、碰撞等力矩的综合作用效果,从而解释各板块运动的驱动机制。
4) 板底剪切力作为一个强黏性约束维持了板块运动的稳定性。由于板底剪切力的数量级很大,板块边界力矩变化时,板块力矩不平衡的调整过程十分迅速。可以通过建立变化前后两个力矩平衡模型进行比较的方法探究古板块运动状态明显变化的原因。
本文对板块力矩的计算建立在简单物理模型之上,计算中参数的选取具有诸多的不确定性,岩石圈密度分层也做了一定的简化。我们将在未来的工作中继续完善模型和数据,更深入细致地研究板块驱动力这一重要的地球动力学课题。
| [1] |
Morgan W J. Rises, trenches, great faults, and crustal blocks[J]. Journal of Geophysical Research, 1968, 73(6): 1959-1982. Doi:10.1029/JB073i006p01959 |
| [2] |
Minster J B, Jordan T H. Present-day plate motions[J]. Journal of Geophysical Research: Solid Earth, 1978, 83(B11): 5331-5354. Doi:10.1029/JB083iB11p05331 |
| [3] |
Chase C G. Plate kinematics: the Americas, East Africa, and the rest of the world[J]. Earth and Planetary Science Letters, 1978, 37(3): 355-368. Doi:10.1016/0012-821X(78)90051-1 |
| [4] |
DeMets C, Gordon R G, Argus D F, et al. Current plate motions[J]. Geophysical Journal International, 1990, 101(2): 425-478. Doi:10.1111/j.1365-246X.1990.tb06579.x |
| [5] |
DeMets C, Gordon R G, Argus D F, et al. Effect of recent revisions to the geomagnetic reversal time scale on estimates of current plate motions[J]. Geophysical Research Letters, 1994, 21(20): 2191-2194. Doi:10.1029/94GL02118 |
| [6] |
DeMets C, Gordon R G, Argus D F. Geologically current plate motions[J]. Geophysical Journal International, 2010, 181(1): 1-80. Doi:10.1111/j.1365-246X.2009.04491.x |
| [7] |
Wilson J T. Evidence from ocean islands suggesting movement in the Earth[J]. Philosophical Transactions of the Royal Society of London. Series A, Mathematical, Physical and Engineering Sciences, 1965, 258(1088): 145-167. Doi:10.1098/rsta.1965.0029 |
| [8] |
Morgan W J. Convection plumes in the lower mantle[J]. Nature, 1971, 230(5288): 42-43. Doi:10.1038/230042a0 |
| [9] |
Morgan W J. Deep mantle convection plumes and plate motions[J]. AAPG bulletin, 1972, 56(2): 203-213. Doi:10.1306/819a3e50-16c5-11d7-8645000102c1865d |
| [10] |
Argus D F, Gordon R G, DeMets C. Geologically current motion of 56 plates relative to the no-net-rotation reference frame[J]. Geochemistry, Geophysics, Geosystems, 2011, 12(11): Q11001. Doi:10.1029/2011GC003751 |
| [11] |
Ricard Y, Doglioni C, Sabadini R. Differential rotation between lithosphere and mantle: a consequence of lateral mantle viscosity variations[J]. Journal of Geophysical Research: Solid Earth, 1991, 96(B5): 8407-8415. Doi:10.1029/91JB00204 |
| [12] |
Conrad C P, Behn M D. Constraints on lithosphere net rotation and asthenospheric viscosity from global mantle flow models and seismic anisotropy[J]. Geochemistry, Geophysics, Geosystems, 2010, 11(5): Q05W05. Doi:10.1029/2009GC002970 |
| [13] |
Wang S M, Yu H Z, Zhang Q, et al. Absolute plate motions relative to deep mantle plumes[J]. Earth and Planetary Science Letters, 2018, 490: 88-99. Doi:10.1016/j.epsl.2018.03.021 |
| [14] |
Sekiguchi S. The magnitude of driving forces of plate motion[J]. Journal of Physics of the Earth, 1985, 33(4): 369-389. Doi:10.4294/jpe1952.33.369 |
| [15] |
Griggs D T. A theory of mountain-building[J]. American Journal of Science, 1939, 237(9): 611-650. Doi:10.2475/ajs.237.9.611 |
| [16] |
Hager B H, O'Connell R J. A simple global model of plate dynamics and mantle convection[J]. Journal of Geophysical Research: Solid Earth, 1981, 86(B6): 4843-4867. Doi:10.1029/JB086iB06p04843 |
| [17] |
Wang S M, Wang R. Current plate velocities relative to hotspots: implications for hotspot motion, mantle viscosity and global reference frame[J]. Earth and Planetary Science Letters, 2001, 189(3/4): 133-140. Doi:10.1016/S0012-821X(01)00351-X |
| [18] |
Forsyth D, Uyedaf S. On the relative importance of the driving forces of plate motion[J]. Geophysical Journal International, 1975, 43(1): 163-200. Doi:10.1111/j.1365-246X.1975.tb00631.x |
| [19] |
Backus G, Park J, Garbasz D. On the relative importance of the driving forces of plate motion[J]. Geophysical Journal International, 1981, 67(2): 415-435. Doi:10.1111/j.1365-246X.1981.tb02758.x |
| [20] |
Chapple W M, Tullis T E. Evaluation of the forces that drive the plates[J]. Journal of Geophysical Research, 1977, 82(14): 1967-1984. Doi:10.1029/JB082i014p01967 |
| [21] |
Harper J F. Forces driving plate tectonics: The use of simple dynamical models[M]. Wellington: Department of Mathematics and Research School of Earth Sciences, Victoria University of Wellington, 1988.
|
| [22] |
Solomon S C, Sleep N H. Some simple physical models for absolute plate motions[J]. Journal of Geophysical Research, 1974, 79(17): 2557-2567. Doi:10.1029/JB079i017p02557 |
| [23] |
Gordon R G, Cox A, Harter C E. Absolute motion of an individual plate estimated from its ridge and trench boundaries[J]. Nature, 1978, 274(5673): 752-755. Doi:10.1038/274752a0 |
| [24] |
Richardson R M. Ridge forces, absolute plate motions, and the intraplate stress field[J]. Journal of Geophysical Research: Solid Earth, 1992, 97(B8): 11739-11748. Doi:10.1029/91JB00475 |
| [25] |
Turcotte D L, Schubert G. Geodynamics[M]. Cambridge: Cambridge University Press, 2014. Doi:10.1017/cbo9780511843877
|
| [26] |
朱照宣, 周起钊, 殷金生. 理论力学[M]. 北京: 北京大学出版社, 1982.
|
| [27] |
Bird P. An updated digital model of plate boundaries[J]. Geochemistry, Geophysics, Geosystems, 2003, 4(3): 1027. Doi:10.1029/2001GC000252 |
| [28] |
Pasyanos M E, Masters T G, Laske G, et al. LITHO1. 0: an updated crust and lithospheric model of the Earth[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(3): 2153-2173. Doi:10.1002/2013JB010626 |
| [29] |
Müller R D, Sdrolias M, Gaina C, et al. Age, spreading rates, and spreading asymmetry of the world's ocean crust[J]. Geochemistry, Geophysics, Geosystems, 2008, 9(4): Q04006. Doi:10.1029/2007GC001743 |
| [30] |
McKenzie D P. Speculations on the consequences and causes of plate motions[J]. Geophysical Journal International, 1969, 18(1): 1-32. Doi:10.1111/j.1365-246X.1969.tb00259.x |
| [31] |
冷伟, 毛伟. 俯冲带热结构的动力学模型研究[J]. 中国科学D: 地球科学, 2015, 45(6): 736-751. |
| [32] |
Stevenson D J, Turner J S. Angle of subduction[J]. Nature, 1977, 270(5635): 334-336. Doi:10.1038/270334a0 |
| [33] |
Conrad C P, Lithgow-Bertelloni C. How mantle slabs drive plate tectonics[J]. Science, 2002, 298(5591): 207-209. Doi:10.1126/science.1074161 |
| [34] |
Schellart W P. Quantifying the net slab pull force as a driving mechanism for plate tectonics[J]. Geophysical Research Letters, 2004, 31(7): L07611. Doi:10.1029/2004GL019528 |
| [35] |
McNutt M K. Lithospheric flexure and thermal anomalies[J]. Journal of Geophysical Research: Solid Earth, 1984, 89(B13): 11180-11194. Doi:10.1029/JB089iB13p11180 |
| [36] |
Lallemand S, Heuret A, Boutelier D. On the relationships between slab dip, back-arc stress, upper plate absolute motion, and crustal nature in subduction zones[J]. Geochemistry, Geophysics, Geosystems, 2005, 6(9): Q09006. Doi:10.1029/2005GC000917 |
| [37] |
Karato S I, Wu P. Rheology of the upper mantle: a synthesis[J]. Science, 1993, 260(5109): 771-778. Doi:10.1126/science.260.5109.771 |
| [38] |
Schellart W P. Evolution of subduction zone curvature and its dependence on the trench velocity and the slab to upper mantle viscosity ratio[J]. Journal of Geophysical Research: Solid Earth, 2010, 115(B11): B11406. Doi:10.1029/2009JB006643 |
| [39] |
Warners-Ruckstuhl K N, Govers R, Wortel R. Lithosphere-mantle coupling and the dynamics of the Eurasian Plate[J]. Geophysical Journal International, 2012, 189(3): 1253-1276. Doi:10.1111/j.1365-246X.2012.05427.x |
| [40] |
Warners-Ruckstuhl K N, Govers R, Wortel R. Tethyan collision forces and the stress field of the Eurasian Plate[J]. Geophysical Journal International, 2013, 195(1): 1-15. Doi:10.1093/gji/ggt219 |
| [41] |
Copley A, Avouac J P, Royer J Y. India-Asia collision and the Cenozoic slowdown of the Indian plate: Implications for the forces driving plate motions[J]. Journal of Geophysical Research: Solid Earth, 2010, 115(B3): B03410. Doi:10.1029/2009JB006634 |
| [42] |
Gordon R G, Jurdy D M. Cenozoic global plate motions[J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B12): 12389-12406. Doi:10.1029/JB091iB12p12389 |
| [43] |
Lithgow-Bertelloni C, Richards M A. The dynamics of Cenozoic and Mesozoic plate motions[J]. Reviews of Geophysics, 1998, 36(1): 27-78. Doi:10.1029/97RG02282 |
| [44] |
Seton M, Müller R D, Zahirovic S, et al. Global continental and ocean basin reconstructions since 200 Ma[J]. Earth-Science Reviews, 2012, 113(3/4): 212-270. Doi:10.1016/j.earscirev.2012.03.002 |
| [45] |
Sharp W D, Clague D A. 50-Ma initiation of Hawaiian-Emperor bend records major change in Pacific plate motion[J]. Science, 2006, 313(5791): 1281-1284. Doi:10.1126/science.1128489 |
| [46] |
Conrad C P, Lithgow-Bertelloni C. The temporal evolution of plate driving forces: Importance of "slab suction" versus "slab pull" during the Cenozoic[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B10): B10407. Doi:10.1029/2004JB002991 |
 2022, Vol. 39
2022, Vol. 39 


