2. 中国科学院大学, 北京 100049;
3. 上海科技大学信息科学与技术学院, 上海 200120
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Information Science and Technology, ShanghaiTech University, Shanghai 200120, China
低轨卫星物联网系统中通信和频谱感知共用天线射频设备,低轨卫星只能在通信间隙感知频谱,因此感知间隔随着通信业务的饱和而增大,并且由于硬件限制以及卫星运行特点使得频谱感知数据的空间分辨率较低。文献[1]指出需要进一步提高频谱数据在时域、频域、空域的分辨率以满足更精确的频谱共享需求。另外频谱数据可用于生成频谱态势,相比频谱数据,在频谱态势中的数据研究的整体性更强,内容更丰富[2-3]。因此在频谱态势可视化的启发下本文提出采用图像超分辨重建算法提高低轨卫星频谱感知数据的空间分辨率。
本文基于低轨卫星星座协同感知[4],首先将分散、孤立的空间频谱感知数据以矩阵形式表示,然后转化为图像,以灰度值呈现接收信号的相对强度,从而直观地观察频谱的空间态势,进而根据转化后的图像特征选择图像超分辨率重建算法,从图像优化角度提高频谱感知数据的空间分辨率。高分辨图像中的像素密度高,图像中的细节更易辨认,相应地频谱中包含的电磁环境信息也更易识别,比如:是否存在信号,信号源的数目等。
采用双三次插值方法[5]提高图像分辨率时,放大图像的过程中可以保持平滑,是插值算法中效果较优的一种超分辨率重建方法。另外基于贝叶斯框架的重建算法中可以直接添加高分辨率图像的先验来约束重建过程,考虑到大部分地面站反射面天线信号辐射呈现波纹状,频谱感知数据图像中的边缘信息丰富,所以采用利于保持边缘的基于L1范数先验的贝叶斯重建算法[6]。另外通过主动学习匹配图像块的SelfExSR算法[7]无需外部数据库,对于细节的重建效果较好,因此采用该方法来增强频谱感知数据图像中的边界。
1 低轨卫星频谱感知数据转化为图像频谱感知可以获取时域、空域、频域、能量域等在内的频谱使用情况,空间频谱信息随着用户数量的增多而与日俱增。以接收信号功率作为频谱强度度量,研究频谱的空间分布情况时,关注由空间位置和接收功率构成的频谱空域切片[8],低轨卫星频谱感知数据的空域切片反映了特定时间特定频率特定高度不同经纬度的电磁分布特性。将多时段多轨多颗卫星的采集数据融合到一幅图像中,会使频谱数据增多的同时增强数据之间的相关性。
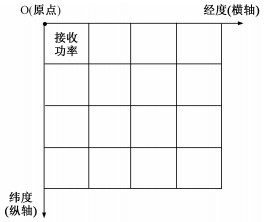
类似于数字图像的矩阵表示方法[9],建立频谱空间坐标系,将频谱数据以矩阵形式表示如图 1所示。由于卫星的轨道特性使得低轨卫星频谱感知数据在经度方向的变化幅度远小于在纬度方向的变化幅度,所以频谱的空间坐标系设置为非均匀,即横纵轴上的单位长度代表的物理尺寸不同。
|
Download:
|
| 图 1 频谱感知数据的矩阵表示 Fig. 1 Matrix representation of the spectrum sensing data | |
获得空间频谱数据构成的二维矩阵后,将其中存储的接收功率归一化处理,然后转化为灰度值,在转化为图像的过程中得到了相对信号强度,类似于频谱感知中的能量检测法[10-13],可以从视觉上直观地判断信号的存在性,如若某处灰度值较高,则可以初步判断该处存在信号。
另外以二维图像形式呈现低轨卫星频谱感知数据的空间分布时,大部分地面站反射面天线信号辐射呈现波纹状。虽然不同的电磁环境下,频谱感知数据的空间分布会呈现出不同的特征,但是都会包含亮点和波纹,尤其频谱数据图像中的波纹即边缘信息更为丰富。
2 图像超分辨率重建算法超分辨率技术是一种图像处理程序[14],旨在由单幅或多幅低分辨率图像恢复出高分辨率图像[15],增强图像细节,增加人眼可分辨的信息量[16],根据不同的输入分为单幅和多幅图像超分辨率重建。在频谱的矩阵表示法中,接收功率与卫星位置一一对应,并且由于卫星运行周期长,电磁环境变化快,所以在提高频谱的空间分辨率时更符合单幅图像超分辨率重建的场景。单幅超分辨率重建方法可分为基于插值、基于重建和基于学习的方法[17]。
基于插值的方法简单易于实现,许多电子设备采用双三次插值方法来放缩图像。双三次插值方法[5]是一种多项式插值方法,计算待求点附近16个点的加权平均。令(x, y)为待求点的位置坐标,v(x, y)表示接收功率值。其计算公式为
| $ v\left( {x, y} \right) = \sum\limits_{i = 0}^3 {\sum\limits_{j = 0}^3 {{a_{ij}}{x^i}{y^j}} } . $ | (1) |
基于令3次卷积插值函数尽可能多地和Taylor级数展开式一致的插值思想来求解16个权重系数aij。
基于重建的方法通过引入高分辨率图像中的先验来保证重建过程中解的存在性和唯一性。基于L1范数的贝叶斯重建方法[6]以横纵方向上的一阶差分的L1范数作为先验模型,并对其中的参数进行估计获得高分辨率图像。
假定LR观测图像为g,未知HR图像为f,那么在给定g下估计f和超参数的贝叶斯框架是基于后验概率分布,可表示为
| $ P\left( {\mathit{\Theta }, f|g} \right) = \frac{{P\left( {\mathit{\Theta }, f, g} \right)}}{{P\left( g \right)}}, $ | (2) |
式中Θ代表模型参数。联合概率分布P(Θ, f, g)在超先验模型P(Θ),先验模型P(f|Θ) 和退化模型P(g|f,Θ)[6],给定下可表示为
| $ P\left( {\mathit{\Theta }, f, g} \right) = P\left( \mathit{\Theta } \right)P\left( {f|\mathit{\Theta }} \right)P\left( {g|f, \mathit{\Theta }} \right), $ | (3) |
先验模型表达式为
| $ \begin{array}{c} P\left( {f, {\alpha ^h}, {\alpha ^v}} \right) = \frac{1}{{Z\left( {{\alpha ^h}, {\alpha ^v}} \right)}} \times \\ {\rm{exp}}\left\{ { - \sum\limits_{i = 1}^p {{\alpha ^h}{{\left\| {{\Delta ^h}_i\left( f \right)} \right\|}_1} + {\alpha ^v}{{\left\| {{\Delta ^v}_i\left( f \right)} \right\|}_1}} } \right\}, \end{array} $ | (4) |
式中: Z(αh, αv)与αhαv成正比,Δih(f)和Δiv(f)表示水平和垂直方向上像素i的一阶差分,αh和αv是模型参数,可分别根据水平和垂直方向上的一阶差分的和求解。在提高频谱感知数据的空间分辨率时,输入为单幅图像,所以无需配准,退化模型为下采样。
文献[7]中提出的SelfExSR算法利用自然图像中的图像块在同一幅图像的尺度内和尺度间反复出现的统计先验知识,通过允许几何变化来扩展内部图像块搜索空间,并加入额外的仿射变换以适应局部形状变化,提高了超分辨率的性能。该方法主动学习图像本身的特征,无需任何外部训练数据库。基于输入的低分辨率图像ILR和对其下采样和模糊的ID, 使用SelfExSR算法求解IHR的流程如下所示。
Algorithm 1 SelfExSR
1)对于LR图像ILR中的每个图像块P(目标图像块),计算转换矩阵T(具有单应性),该矩阵将P扭曲为下采样图像ID中的最佳匹配图像块Q(源图像块)。为了获得转换参数,使用改进的PatchMatch算法[18]估计ILR和ID之间的最近邻域。
2)从图像ILR中提取QHR(源图像块的HR版本)。
3)使用计算出的转换矩阵T的逆来“展开”HR版本的QHR,以获得PHR(估计出的目标图像块P的HR版本), 将HR图像IHR粘贴到LR图像块P对应的位置。
4)对所有目标图像块重复上述步骤以获得HR图像IHR的估计值。
5)运行迭代反投影算法[19]以确保估计的IHR满足给定LR观测ILR的重建约束。
由于基于学习和基于重建的方法相较于基于插值的方法利用了额外的先验知识,所以理论上基于L1范数先验的贝叶斯方法和SelfExSR算法的效果优于双三次插值方法。基于L1范数先验的贝叶斯方法利于保持图像边缘,由于空间频谱感知数据构成的二维图像中存在丰富的边缘信息,所以该方法适用于提高频谱感知数据的空间分辨率。另外频谱感知数据的空间分布往往会以信号源为中心四周对称,其波纹之间呈现出一定的相似性,SelfExSR算法基于图像本身具有相似性的假设,并通过匹配图像块来提高分辨率,所以在增强细节方面会有不错的效果。
3 实验及结果低轨卫星物联网系统中,地面站作为用频设备,向空间发射信号,低轨卫星作为频谱感知设备运行在轨道上采集频谱信息。卫星通信的无线信道通常被认为是在自由空间传播的,根据自由空间传播模型计算接收功率,其中信号的发射功率均为30 dBW,通过计算仰角并查询由卫星工具包(satellite tool kit,STK)导出的发射天线方向图获取发射天线增益。
仿真产生经度介于[114°,118°],纬度介于[20°,60°],高度为780 km的空间矩形区域内的频谱感知数据,以目标区域内400×400个网格的数据作为空间高分辨率数据,然后通过下采样获得低分辨率数据。
3.1 目标区域中不同场景下的高分辨率频谱感知数据图 2(a)~2(c)为1个信号源场景下目标区域中的高分辨率频谱感知数据。该信号源位于(116°E, 40°N),发射频率为12.001 GHz,发射天线增益分别为30、40和50 dB。

|
Download:
|
| 图 2 不同场景下的高分辨率频谱感知数据 Fig. 2 High-resolution spectrum sensing data in different scenarios | |
图 2(d)~2(f)为2个信号源场景下目标区域中的高分辨率频谱感知数据。2个信号源分别位于(116°E,40°N)和(116.2°E,39°N),发射频率为12.001和12 GHz,发射天线增益依次分别为(40 dB,30 dB)、(40 dB,40 dB)、(40 dB,50 dB)。
对目标区域中不同场景下的高分辨率频谱感知数据进行分析:频谱感知数据图像中均包含光圈和波纹,并且随着天线增益的增加,光圈缩小,波纹更加密集,另外信号源个数可以直接观察光圈个数进行判断。
3.2 频谱感知数据的超分辨率重建首先对1个信号源的频谱感知数据进行2倍超分辨率重建,仿真场景为:信号源位于(116°E, 40°N),发射频率为12.001 GHz,发射天线增益为39.394 6 dB。结果列于图 3。

|
Download:
|
| 图 3 单个信号源场景中频谱感知数据的超分辨率重建 Fig. 3 Super-resolution reconstruction of spectrum sensing data in a single signal source scenario | |
峰值信噪比PSNR基于均方误差MSE,通过计算每一点对应的欧式距离并求平均,因此经常被用于评价重建的整体效果。双三次插值、基于L1范数先验的贝叶斯方法和SelfExSR方法都能有效地提高频谱感知数据的空间分辨率,根据表 1中的PSNR值,3种方法中基于L1先验的贝叶斯方法的重建效果更好一些。从视觉效果上来评价,SelfExSR方法中的波纹更为清晰。采用超分辨率重建方法在保持细节的前提下放大图像尺寸,通过图像处理提高了频谱感知数据的空间分辨率。
|
|
表 1 不同重建方法在单个信号源场景中的性能比较 Table 1 Performance comparison of different reconstruction methods in a single signal source scenario |
然后通过增加信号源提高空间频谱感知数据的复杂度,仿真场景为:2个信号源分别位于(116°E,40°N)和(116.2°E, 39°N),发射频率为12.001和12 GHz,发射天线增益均为39.394 6 dB。根据表 2中不同算法的PSNR值,基于L1范数先验的贝叶斯方法和SelfExSR算法的重建效果均优于双三次插值方法,基于L1范数先验的贝叶斯方法略优于SelfExSR算法。但是通过图 4在视觉上观察细节,可以直观地看到SelfExSR算法重建结果中,光圈之间的边界更为清晰。
|
|
表 2 不同重建方法在2个信号源场景中的性能比较 Table 2 Performance comparison of different reconstruction methods in two signal source scenarios |

|
Download:
|
| 图 4 2个信号源场景中频谱感知数据的超分辨率重建 Fig. 4 Super-resolution reconstruction of spectrum sensing data in two signal source scenarios | |
本文将图像超分辨率重建技术应用到多颗低轨卫星作为感知源获取的低空间分辨率频谱数据中,从图像优化的角度提高了频谱感知数据的空间分辨率。实验表明:通过图像形式研究频谱感知数据,更具有整体性,观察频谱态势也更直观。采用图像超分辨率重建算法提高频谱数据的空间分辨率,简单易行并且取得了不错的效果。
通过优化图像,提高了频谱感知数据的空间分辨率并且也保持了频谱感知数据中潜在的细节。另外由于空间的频谱感知数据本身就构成了空间频谱态势,所以相应地也提高了频谱态势的精度,利于更精确地分析电磁环境,助于频谱管理和指导用频。
| [1] |
杨健, 陈曦, 丁国如, 等. 基于区块链的频谱设备网络中防御拜占庭攻击的分布式共识机制[J]. 通信学报, 2020, 41(3): 1-16. Doi:10.11959/j.issn.1000-436x.2020044 |
| [2] |
李竟铭. 面向频谱地图构建的频谱态势生成技术研究[D]. 南京: 南京航空航天大学, 2019.
|
| [3] |
吴启晖, 任敬. 电磁频谱空间认知新范式: 频谱态势[J]. 南京航空航天大学学报, 2016, 48(5): 625-632. Doi:10.16356/j.1005-2615.2016.05.002 |
| [4] |
王运峰, 丁晓进, 张更新. GEO与LEO双层网络协同频谱感知研究[J]. 无线电通信技术, 2019, 45(6): 627-632. Doi:10.3969/j.issn.1003-3114.2019.06.010 |
| [5] |
Keys R G. Cubic convolution interpolation for digital image processing[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(6): 1153-1160. Doi:10.1109/TASSP.1981.1163711 |
| [6] |
Villena S, Vega M, Molina R, et al. Bayesian super resolution image reconstruction using an ℓ1 prior[C] // 2009 Proceedings of 6th International Symposium on Image and Signal Processing and Analysis, Seprember 16-18, 2009, Salzburg, Austria. IEEE, 2009: 152-157. DOI: 10.1109/ISPA.2009.5297740.
|
| [7] |
Huang J B, Singh A, Ahuja N. Single image super-resolution from transformed self-exemplars[C]// 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 7-12, 2015, Boston, MA, USA. IEEE, 2015: 5197-5206. DOI: 10.1109/CVPR.2015.7299156.
|
| [8] |
何国金. 频谱态势三维可视化技术研究[J]. 电子制作, 2013(7): 36-37. Doi:10.16589/j.cnki.cn11-3571/tn.2013.07.004 |
| [9] |
Gonzalez R C, Woods R E. 数字图像处理[M]. 3版. 阮秋琦, 阮宇志译. 北京: 电子出版社, 2011: 31-38.
|
| [10] |
Kim K, Xin Y, Rangarajan S. Energy detection based spectrum sensing for cognitive radio: an experimental study[C]//2010 IEEE Global Telecommunications Conference GLOBECOM 2010. December 6-10, 2010, Miami, FL, USA. IEEE, 2010: 1-5. DOI: 10.1109/GLOCOM.2010.5683560.
|
| [11] |
Sofotasios P C, Rebeiz E, Zhang L, et al. Energy detection based spectrum sensing over κ-μ and κ-μ extreme fading channels[J]. IEEE Transactions on Vehicular Technology, 2013, 62(3): 1031-1040. Doi:10.1109/TVT.2012.2228680 |
| [12] |
Gismalla E H, Alsusa E. A generalized system model and performance analysis for the periodogram-based energy detector[C]//2011 IEEE Global Telecommunications Conference-GLOBECOM 2011. December 5-9, 2011. Houston, TX, USA. IEEE, 2011: 1-5. DOI: 10.1109/GLOCOM.2011.6134146.
|
| [13] |
Alsusa E, Gismalla E H. An accurate model for periodogram-based energy detection over Nakagami fading[C]// 2012 IEEE International Conference on Communications (ICC). June 10-15, 2012, Ottawa, ON, Canada. IEEE, 2012: 1614-1618. DOI: 10.1109/ICC.2012.6364019.
|
| [14] |
李欣, 崔子冠, 朱秀昌. 超分辨率重建算法综述[J]. 电视技术, 2016, 40(9): 1-9. Doi:10.16280/j.videoe.2016.09.001 |
| [15] |
Liu X, Guo T D, Han C Y, et al. Super resolution reconstruction of single image with denoising and upscaling[J]. Journal of University of Chinese Academy of Sciences, 2016, 33(5): 596-603. Doi:10.7523/j.issn.2095-6134.2016.05.004 |
| [16] |
何保畅, 耿修瑞, 胡文龙. 一种基于视觉特性和灰度补偿改进的LDR图像增强方法[J]. 中国科学院大学学报, 2018, 35(3): 391-401. Doi:10.7523/j.issn.2095-6134.2018.03.014 |
| [17] |
Yang W M, Zhang X C, Tian Y P, et al. Deep learning for single image super-resolution: a brief review[J]. IEEE Transactions on Multimedia, 2019, 21(12): 3106-3121. Doi:10.1109/TMM.2019.2919431 |
| [18] |
Barnes C, Shechtman E, Finkelstein A, et al. PatchMatch: a randomized correspondence algorithm for structural image editing[J]. ACM Transactions on Graphics, 2009, 28(3): article24. Doi:10.1145/1531326.1531330 |
| [19] |
Irani M, Peleg S. Improving resolution by image registration[J]. CVGIP: Graphical Models and Image Processing, 1991, 53(3): 231-239. Doi:10.1016/1049-9652(91)90045-L |
 2022, Vol. 39
2022, Vol. 39 


