分类问题一直是机器学习领域经久不衰的话题。目前有监督分类方法已经相对成熟，其中不少方法在某些数据集上已经达到非常高的准确率。近年来，深度学习社区的活跃研究已经催生出许多使用深度神经网络去做分类的成功案例^[1-3]。这些方法均需要经过以下3个过程：数据压缩，特征提取和模型预测。这些过程往往依赖于大量的数据标注，但现实生活中标注好的数据十分稀缺。因此，无监督和半监督学习顺势兴起。在无监督学习中，数据的分布p(x)与条件分布p(y| x)有一定的联系，其中x表示数据，y∈{1, …, K} $ \buildrel \Delta \over = $ [K]表示未知的数据标签。不同于有监督学习，无监督学习中标签信息p(y)无法直接获得，因此只能利用数据的结构特征推断训练样本的标签。作为无监督学习家族的重要一员，无监督分类通常建模为聚类问题，并且已经具有一些经典的方法：K-means、Gaussian mixture model、density estimation，这些方法均是针对数据分布进行建模。此外，一些判别式方法比如maximum margin clustering (MMC)^[4]、regularized information maximization (RIM)^[5]，则是将数据划分到某个类别，无须估计数据分布。尽管判别式方法更为直接，但是它们容易受一些虚假相关性的影响而产生过拟合^[6]。当与深度神经网络这种拟合能力很强的模型相结合的时候，过拟合现象尤为显著。随着深度学习领域崛起^[7-9]，越来越多的学者使用深度模型研究无监督或半监督学习。这些方法通常是训练一个生成式模型，比如波尔兹曼机^[10-11]、前馈神经网络^[12-13]以及自编码器^[14-15]，通过重建输入样本学习数据特征，刻画数据分布。这类方法避免了因直接划分数据而产生的过拟合问题，但是在重建训练样本的过程中没有额外的约束，所以会保留原始数据的所有信息，这和训练分类器的目标相背^①

① 在训练分类器时, 通常只希望保留和分类目标相关的信息, 从而使得模型对其他不重要的信息更加鲁棒。

生成对抗网络(generative adversarial network，GAN)^[16]是最近非常热门的研究课题之一。相较于纯生成式模型，GAN训练生成器的同时，还训练一个判别器，通过二者对抗使得生成器学习到真实数据分布并生成较为逼真的数据。InfoGAN^[17]通过最大化隐变量和生成图片之前的互信息，能够学习到数据的局部特征，从而调控生成图片的样式。CatGAN^[6]利用生成对抗网络模型，将生成式方法和判别式方法相结合，在MNIST^[18]和CIFAR-10^[19]上均取得了十分可观的分类准确度。Li等^[20]指出，良好的分类准确率和良好的生成效果互不相容，进而提出具有3个模块的GAN模型。EnhancedTGAN^[21]在TripleGAN的基础上额外增加一个分类器，并重新设计目标函数，达到了更好的效果。由于增加了分类专用网络，所以基于TripleGAN的模型无法进行无监督学习。

本文将InfoGAN和CatGAN相结合，提出InfoCatGAN模型。CatGAN只关注分类精度，仅仅将判别器作为提取特征的工具，以致生成的图片不够逼真。InfoGAN可以指定生成图片的特征，对分类有指导作用。两者结合，InfoCatGAN能够通过超参数λ的设置，实现分类准确率和生成数据逼真度的折中，即当λ较小时，分类准确度较高，但生成图片质量较差；当λ较高时，生成图片质量较高，分类准确率较低。为了简化模型，同时避免超参数不确定性所带来的影响，本文基于InfoGAN提出Classifier InfoGAN(C-InfoGAN)，该模型可以在牺牲少量的分类准确率的情况下，获得更高的生成质量。二者均可以对生成图片的类别进行调控，此外C-InfoGAN能够对图片局部特性进行调整，如改变字体粗细、倾斜度等(见图 1)，这对指定特征的数据补足有较大意义。与TripleGAN和EnhancedTGAN相比，本文提出的基于互信息约束的模型支持无监督分类，且能够调节生成图片的局部特征，与此同时还具有更强的可解释性。

1 生成对抗网络

生成对抗网络由Goodfellow等^[16]在2014年提出，在该模型中，他们训练一个生成器G—给定噪声生成虚假数据，和一个判别器D—给定输入判别其真假。训练过程可以类比为两个玩家博弈：判别器读取一个数据希望能够分别真假，而生成器希望生成以假乱真的数据从而让判别器判定为真。

在实际应用中，生成器和判别器通常实现为可微的深度神经网络。设χ ={ x₁, …, x_N}为真实数据集，其中x_i=(x_i1, …, x_in)∈ Rⁿ，z =(z₁, …, z_m)∈ R^m为按分布p_z采样的隐空间噪声，其中N为样本个数，n为单个样本的维度，m为噪声维度。可以将生成器描述为G: R^m $ \mapsto $ Rⁿ，将判别器描述为D: Rⁿ$ \mapsto $(0, 1)，其中D(x)表示x来自真实数据分布的概率。对于给定的G，训练D使得对于真实数据x，D(x)接近于1；对于虚假数据$ \tilde{\boldsymbol{x}}=G(\boldsymbol{z}), D(\tilde{\boldsymbol{x}})$接近于0。当D训练至最优，固定D训练G以降低判别器对于虚假数据的区分精度。当生成器对应的概率分布p_g与真实数据的分布p_data完美契合的时候，D无法分别真假，对于所有输入都输出0.5的概率。综上所述，GAN的目标函数如下

$ \begin{aligned} &\min _{G} \max _{D} V_{G A N}(D, G)= \\ &\mathbb{E}_{x-p_{\text {data }}}[\log D(\boldsymbol{x})]+\mathbb{E}_{z \sim p_{z}}[\log (1-D(G(z)))] . \end{aligned} $

(1)

1.1 InfoGAN

原始的GAN没有对输入噪声z做任何限制，这使得生成器在生成虚假数据时没有指向性，以至于生成的数据高度耦合，数据特征难以解释。InfoGAN将噪声分解为两部分：一部分依然是无结构的噪声z ~p_z，为模型提供足够的容量；另一部分作为隐变量c ~p_c，用于学习数据的特殊语义。InfoGAN最大的创新是引入互信息约束，通过最大化隐变量c与生成数据$ \mathit{\boldsymbol{\tilde x}} = G(\mathit{z},\mathit{\boldsymbol{c}})$之间的互信息

$ I(\mathit{\boldsymbol{c}};\mathit{\boldsymbol{\tilde x}}) = H(\mathit{\boldsymbol{c}}) - H(\mathit{\boldsymbol{c}}\mid {\rm{ }}\mathit{\boldsymbol{\tilde x}}), $

(2)

将隐变量绑定到数据的某些特征，H(·)表示Shannon熵。在信息论中，互信息I(X; Y)用来衡量在观测到随机变量X之后，随机变量Y的不确定性的减少量。互信息越大说明两个变量之间的关系越紧密，反之互信息为0，则说明变量间相互独立。InfoGAN将互信息作为正则项加入其目标函数

$ \begin{aligned} \min _{G, Q} \max _{D} &\;\;\;V_{\text {InfoGAN }}(G, D, Q, \lambda)=\\ &\;\;\;V_{\mathrm{GAN}}(G, D)-\lambda I(\boldsymbol{c} ; \tilde{\boldsymbol{x}}) \\ I(\boldsymbol{c} ; \tilde{\boldsymbol{x}})=& \mathbb{E}_{p(c, \tilde{\boldsymbol{x}})}\left[\log \frac{Q(\boldsymbol{c} \mid \tilde{\boldsymbol{x}})}{p_{c}(\boldsymbol{c})}\right]+\\ & \mathbb{E}_{p_{g}}\left[D_{\mathrm{KL}}(p(\boldsymbol{c} \mid \tilde{\boldsymbol{x}}) \| Q(\boldsymbol{c} \mid \tilde{\boldsymbol{x}}))\right] \\ & \geqslant \mathbb{E}_{p(c, \tilde{\boldsymbol{x}})}[\log Q(\boldsymbol{c} \mid \tilde{\boldsymbol{x}})]+H(\boldsymbol{c}) \\ & \triangleq L_{I}(Q(\boldsymbol{c} \mid \tilde{\boldsymbol{x}})), \end{aligned} $

(3)

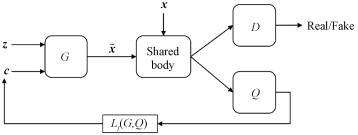
其中: Q是辅助网络用于估计后验概率P(c | x)，λ是正则化系数，D_KL表示Kullback-Leibler距离用于衡量两个概率分布间的差异。而由于在实现中互信息难以计算，故采用其变分下界L_I代替^[22]，其中H(c)在训练过程中视为常量，在实现中可以略去，模型结构见图 2。

1.2 CatGAN

与原始的GAN不同，CatGAN基于合理的假设重新设计了目标函数，并将判别器扩展为多类别分类器。考虑如下无监督分类问题，假设真实数据集χ有K个类别，CatGAN训练一个判别器$ D:{{\bf{R}}^\mathit{n}} \mapsto {({\rm{0}},{\rm{1}})^K}, $给定一个数据x，D(x)给出该数据属于每个类别的概率p(y| x)，且$ \sum\limits_{k = 1}^K p \left( {y = k\mid \mathit{\boldsymbol{x}}} \right) = 1$CatGAN的判别器损失函数L_D^cat和生成器损失函数L_G^cat形式如下：

$ \begin{array}{l} L_D^{{\rm{cat }}} = - {H_x}(p(y)) + {{\mathbb{E}}_{x～{p_{{\rm{data }}}}}}[H(p(y\mid \mathit{\boldsymbol{x}}))] - \\ \;\;\;\;\;\;\;\;\;{{\mathbb{E}}_{\tilde x～{p_g}}}[H(p(y\mid \mathit{\boldsymbol{\widetilde x}}))],\\ L_G^{{\rm{cat }}} = - {H_G}(p(y)) + {{\mathbb{E}}_{\mathit{\boldsymbol{\widetilde x}}～{p_g}}}[H(p(y\mid \mathit{\boldsymbol{\widetilde x}}))]. \end{array} $

(4)

式中各项的计算方式请参考文献[6]，模型结构见图 3。

2 InfoCatGAN 2.1 无监督分类方法

在训练概率分类模型的过程中，通过优化条件熵可以将分类边界调整到更自然的位置(数据分散区域)^[23]，因此CatGAN使用条件熵作为判别器判断真假数据的依据。但是，使用熵作为目标函数的一个缺点是没有类别指向性(K个类别中任意一个都可以使p(y| x)呈单峰分布)。对于一个分类器，理想的情况是对于给定输入x，有且仅有一个k∈[K]，p(y=k| x)能够到达最大，而对于任意k′≠k, p(y=k′| x)均很小。然而问题在于训练数据集没有标注，每个数据样本对应的标签无从获得。

对于上述问题，本文从InfoGAN中获得启发，提出InfoCatGAN模型。InfoGAN将输入噪声划分为z和c，实际上是对隐空间的结构进行人为划分。一部分提供模型的容量，使得模型具有足够的自由度去学习数据的细节(高度耦合的特征)；一部分提供隐变量，用于在学习过程中绑定到数据的显著特征(如：MNIST中的数字类别、笔画粗细、角度)。模型的核心思想如下：通过在隐空间构造一维隐变量c，在训练过程中将生成数据的类别标签与之绑定，使得可以通过c来控制生成数据的类别。CatGAN对GAN的扩展主要在于改变了判别器的输出结构：为所有真实数据分配一个类别标签而对于虚假数据则保持一个不确定的状态。类似地，生成器应该致力于生成某个具体类别的数据而不是仅仅生成足够逼真的图片。

下面给出InfoCatGAN的损失函数：设x ∈ χ为一个真实数据样本，$ \tilde{\boldsymbol{x}}=G(z, c)$为一个生成数据，其中z ~p_z为噪声，c~p_c为隐变量。为了简单起见，这里只考虑c为一维离散随机变量，p_c为离散均匀分布。生成器G=G(z, c; θ_G)和判别器D=D(x; θ_D)均为可微深度神经网络，其中θ_G, θ_D分别为生成器和判别器的参数^①。通过在D网络的最后一层做Softmax变换，可以直接将D(x)作为条件概率p(y| x)的估计。注意到式(4)可以重写为

$ \begin{aligned} L_{D}^{\text {cat }} &=-I(\boldsymbol{x} ; y)-\mathbb{E} _{\tilde{x} \sim p_{g}}[H(p(y \mid \tilde{\boldsymbol{x}}))], \\ L_{G}^{\text {cat }} &=-I(\tilde{\boldsymbol{x}} ; y), \end{aligned} $

(5)

① 为简便起见, 在无歧义的情况下通常省略网络参数。

其中：x ~p_data, $ \tilde{\boldsymbol{x}} \sim p_{g}$分别表示真实数据和虚假数据对应的随机变量，y表示未知标签对应的随机变量。可以看到，CatGAN其实是在优化数据与标签之间的互信息。互信息是常用的变量间相关性的衡量标准，所以用它作为生成器损失函数的正则项，由此得到InfoCatGAN的损失函数如下

$ \begin{aligned} &L_{D}=L_{D}^{\text {cat }} \\ &L_{G}=L_{G}^{\text {cat }}-\lambda_{1} I(c ; \tilde{\boldsymbol{x}}), \end{aligned} $

(6)

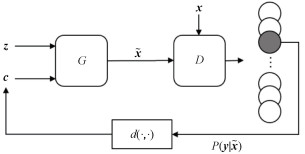
其中λ₁为正则系数，可知当λ₁=0时，InfoCatGAN退化为CatGAN，模型结构见图 4。图中D的输出为P(y|·)。在训练生成器的时候，将判别器的输出$ P(y \mid \tilde{\boldsymbol{x}})$和隐变量c通过某种度量d(·, ·)建立联系使得条件概率的峰值与c的取值对应。参考式(3)，$ I(c;\mathit{\boldsymbol{\tilde x}})$可以放缩为$ \mathbb{E}_{p(c, \tilde{x})}[\log p(c \mid \tilde{x})], $在实现中通常使用交叉熵

$ CE[\mathit{\boldsymbol{c}}, p(\mathit{\boldsymbol{c}}\mid \mathit{\boldsymbol{\widetilde x}})] = - \sum {_{i = 1}^K} {c_i}\log p\left( {c = {c_i}\mid \mathit{\boldsymbol{\widetilde x}}} \right) $

(7)

来优化此项，这里的c ∈ R^K是隐变量c经过one-hot编码之后的向量，$ p(c \mid \tilde{\boldsymbol{x}})$可以用$ D(\tilde{x})$来近似。

2.2 半监督分类方法

作为CatGAN的扩展，InfoCatGAN可以很自然地适用于半监督的情况。假设$ \mathcal{X}^{L}=\left\{\boldsymbol{x}_{i}^{L}\right\}_{i=1}^{m}$为m个有标签的样本，y_i^L∈ R^K为经过one-hot编码之后的标签向量。对于有标签的样本，D(x^L)的分布信息可以明确获得，所以可以通过计算y^L和p(y | x^L)之间的交叉熵

$ CE\left[ {{\mathit{\boldsymbol{y}}^L}, p\left( {\mathit{\boldsymbol{y}}\mid {\mathit{\boldsymbol{x}}^L}} \right)} \right] = - \sum {_{i = 1}^K} {y_i}\log p\left( {y = {y_i}\mid {\mathit{\boldsymbol{x}}^L}} \right), $

(8)

辅助判别器做出更精确的判断。半监督版本的InfoCatGAN损失函数如下

$ L_D^L = {L_D} + \left( {{\mathit{x}^L}, {\mathit{y}^L}} \right)~{{\cal X}^L}\left[ {CE\left[ {{\mathit{\boldsymbol{y}}^L}, p\left( {\mathit{\boldsymbol{y}}\mid {\mathit{\boldsymbol{x}}^L}} \right)} \right]} \right], $

(9)

生成器的损失函数同式(6)：L_G^L=L_G.

3 C-InfoGAN

InfoCatGAN无法同时获得较高的准确率和生成质量，只能通过正则系数λ₁实现二者的性能折中。考虑到InfoGAN模型中的隐变量可以较好地绑定到数据的类别特征，而且生成的图片较为逼真，本文提出C-InfoGAN模型，旨在保证生成质量的前提下，尽可能提高分类准确率。

3.1 无监督分类方法

InfoGAN能够做到无监督地学习数据类别的特征，并且可以通过隐变量控制生成数据的类别，这为分类任务提供了基础。InfoGAN中使用一个辅助的Q网络来估计后验概率P(c | x)，如果隐变量c =(c, c₁, c₂, …)中的c能够学习到数据的类别特征，则可以利用Q(c| x)作为一个概率分类器。具体来说，本文在InfoGAN的目标函数上添加一个正则项$ L(c, \hat{c})$，其中$ \hat{c}=Q(c \mid \tilde{\boldsymbol{x}}) \in \bf{R}^\mathit{K}$是Q网络的输出。称这个分类模型为C-InfoGAN (CIG)，其目标函数如下

$ \begin{aligned} \min _{G, Q} \max _{D} &\;\;\;V_{\mathrm{CIG}}\left(G, D, Q, \lambda_{1}, \lambda_{2}\right)=\\ &\;\;\;V_{\mathrm{InfoGAN}}\left(G, D, Q, \lambda_{1}\right)+\lambda_{2} L(c, Q(c \mid \tilde{\boldsymbol{x}})), \end{aligned} $

(10)

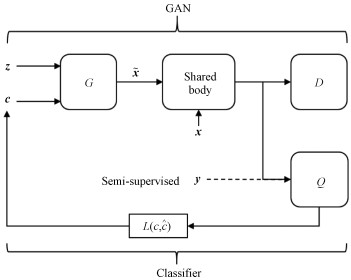
其中: λ₂是正则化系数，$ L(c, \hat{c})=L(c, Q(c \mid \tilde{\boldsymbol{x}}))$在实现中一般采用交叉熵，参见式(8)，模型结构见图 5。无监督情况下，生成数据$ \tilde{\boldsymbol{x}}$和真实数据x参与训练，通过和D共享部分结构，Q网络可以将GAN模型学习到的特征加以利用，实现分类任务。

3.2 半监督分类方法

当拥有少量标签信息时，C-InfoGAN可以利用这些标签进一步提升分类准确率和生成效果。同时将隐变量c直接绑定到真实的标签，实现精准调控。针对少量标注信息，文献[24]提出将隐变量c进一步分解为无监督部分c_us，负责捕捉大量无标注数据的潜在特征；和有监督部分c_ss，负责捕捉已有标签y。同时他们设置了两组隐变量对应的先验分布，以及对应的辅助网络Q_us和Q_ss，使用隐变量c_ss和辅助网络Q_ss专门处理那部分有标注信息。本文直接将标签信息加入Q网络，先用真实数据和标签训练，接着用生成数据和虚假标签(即隐变量c)来训练。这样可以使真实标签的信息流入隐变量c中，即用真实标签指导c绑定到正确的类别特征。经过实践发现，使用上述方法也能达到同样的效果，而且模型更为简单。使用和2.2节中类似的方法，给出半监督C-InfoGAN(ss-CIG)的目标函数如下

$ \begin{aligned} \min _{G, Q} \max _{D} &\;\;\;V_{\mathrm{ss}-\mathrm{CIG}}\left(G, D, Q, \lambda_{1}, \lambda_{2}\right)=\\ &\;\;\;V_{\mathrm{CIG}}\left(G, D, Q, \lambda_{1}, \lambda_{2}\right)+\\ &\;\;\;\mathbb{E}_{\left(x^{L}, (y^{L}\right) \sim x^{L}}\left[C E\left[\boldsymbol{y}^{L}, Q\left(\boldsymbol{y} \mid \boldsymbol{x}^{L}\right)\right]\right], \end{aligned} $

(11)

模型结构参见图 5。在半监督情况下，一部分真实标签y会直接被Q网络利用，以得到更好的效果。优化Q网络的输出$ {\mathit{\hat c}}$和隐变量c构成的损失函数$ L(c, \hat{c})$来增加Q的分类准确率。

4 实验结果与分析

在所有实验中，本文考察两个指标：分类准确率和图片生成质量。对于分类准确率，计算模型预测值并不像一般分类器那样直接。隐变量虽然可以学习到数据类别的特征，但是其取值并不和真实标签正确对应(例如c=1可能对应生成真实标签2的数据)，因此无法直接使用隐变量的取值作为模型的预测值，必须将隐变量的取值与真实标签之间做一个映射。对于这个问题，本文采取与文献[6]相同的做法：在测试集上选取一批样本计算模型在这批数据上的预测值。模型为每一个数据分配一个虚假标签l_i, i∈[K]，然后将预测值和真实标签对比：将虚假标签落入最多的真实标签的取值作为该虚假标签的取值。比如在所有10个被分类为虚假标签l₃的样本中，有9个真实标签为类别‘7’，则将虚假标签l₃映射到真实类别‘7’。对于图片生成质量，本文采用Fréchet inception distance (FID)^[25]进行衡量^①，相较于Inception Score^[26]只考虑生成数据，FID还利用了真实数据，因此更能反映生成数据和真实数据的差异。FID越小代表生成的图片和真实图片越接近，生成质量越好。

① FID一般用于彩色图片, 而MNIST数据集是单通道的灰度图片, 本文将单通道复制3份形成RGB彩色图片计算其FID值。

4.1 MNIST

MNIST是常用的衡量生成式模型的数据集，它包含了60 000张手写数字图片，并且附有类别标签。

图 6(a)和6(b)是在无监督情况下CatGAN和InfoCatGAN的生成效果，其中每一行对应隐变量c的一个取值，从0到9。可以看到，InfoCatGAN的生成效果略高于CatGAN，并且每一行基本是一种数字类别，对应隐变量的不同取值。半监督情况下有类似的结果，不同的是在少量标签信息的辅助下，InfoCatGAN可以将隐变量c和真实标签正确绑定，例如，c=1对应生成数字‘1’，见图 6(e)。CatGAN生成的图片质量较差，原因在于其目标函数是为了分类而设计的。生成器的作用只是为了判别器能够更加鲁棒，如2.1节所述，从式(4)中可以看到，G的目标函数只有条件熵，无法针对性地生成图片，从而会降低生成图片的质量。而InfoCatGAN由于增加了隐变量c，并在训练过程中有意识地将生成数据的类别与之绑定，所以生成的图片质量较好。

图 6(c)和6(f)给出了无监督和半监督情况下C-InfoGAN的生成结果。从图中可以看出无监督情况下，模型已经达到了很好的生成效果，隐变量c基本可以控制生成图片的类别，但是仍有部分类别未能精确控制(图 6(c))；在半监督情况下，隐变量达到了精确的绑定，每一行对应生成一种类别的数字，而且顺序和真实标签是对应的。另外从图 1可以看出，C-InfoGAN模型不仅可以生成指定类别的图片，并且可以通过额外的隐变量调节图片局部特征，如手写数字的粗细、角度等，这对指定特征的数据补足具有一定意义。

表 1给出了无监督和半监督情况下的分类准确率^①和FID。从表中看出，InfoCatGAN的分类准确率虽略低于CatGAN，但在图像生成质量上InfoCatGAN均一致高于CatGAN，这说明增加互信息约束可以提高图像的生成质量。相较于CatGAN模型，C-InfoGAN模型可以获得更高的准确率和生成质量，而且隐变量的绑定效果也更好。而在无监督情况下，C-InfoGAN在保证生成质量的前提下，仍然能够达到87.59 % 的分类准确率。这是因为InfoGAN模型使用的是一个辅助网络Q来做类别绑定和分类任务，训练过程中并没有判别器做过多约束，所以无论如何调整分类网络或更改分类约束，也不会对生成效果产生很大影响。这使得模型可以进一步利用生成的图片和标签扩充数据集，以达到更进一步的性能提升。

① 表中有关CatGAN的数据来自本文复现的结果，与文献[5]有所差距。

表 2给出了正则系数λ₁的不同取值对于半监督InfoCatGAN的影响。从表中可以看出，当系数较小时，分类准确率较高，但生成图片的质量非常差；当系数较大时，生成的图片效果很好，但分类准确率有所降低。通过调节参数λ₁，可以实现生成效果和分类准确率之间的折中。实验使用的默认值是λ₁=0.9，当λ₁减小时，生成图片的质量开始下降，同时分类准确率也会相应增加；当λ₁=0时，InfoCatGAN退化为CatGAN。

4.2 FashionMNIST

FashionMNIST^[27]是一个类似MNIST的数据集，二者拥有同样的图像大小，同样的类别数目。但是相对于MNIST，FashionMNIST拥有更复杂的图像结构，以及更难获得非常高的分类准确率，所以对模型更具有检验性。

表 1给出了模型在FashionMNIST的数值结果。从表中可以看出，在无监督条件下，InfoCatGAN较CatGAN在分类准确率和生成质量上均有所提升，C-InfoGAN在一定程度上兼顾二者，不仅生成质量最优，而且具有相对较高的分类准确率，此外其模型复杂度也较低。在半监督条件下，C-InfoGAN在两个方面均体现出优势，分类准确率达到75.40 %，FID为15.99，生成效果见图 7(f)。

图 7给出了所有模型的生成结果，其中每一行对应隐变量c的一个取值。值得一提的是，加入互信息约束的半监督版本(图 7(e)、7(f))的模型从上往下每一行都对应同一个类别，并且顺序和训练数据的真实标签正确对应。这说明隐变量正确绑定到类别特征，并且可以精准调控生成图片的类别。

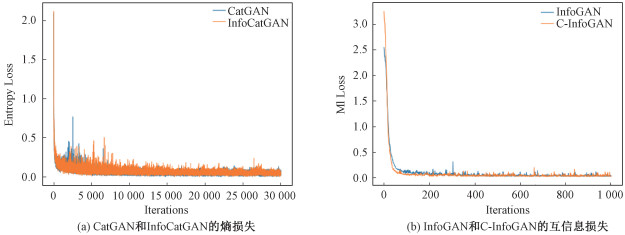
4.3 收敛速度分析

本文提出的两个模型在原理上都属于正则化生成对抗网络，与原先的两个模型CatGAN和InfoGAN相比，增加的计算复杂度较小。由于GAN的训练方式特殊，训练的过程是生成器和判别器的对抗，因此目前没有一个统一的评判收敛性的标准。针对InfoCatGAN和C-InfoGAN两种模型，本文分别用条件熵损失(即判别器输出的概率分布对应的熵)以及互信息损失(实际采用交叉熵估计，详见3.1节)作为模型收敛的佐证，见图 8。

4.4 模型可解释性

从以上结果可以看出，加入互信息约束可以给模型带来许多增益，其中最为显著的是生成质量的提升。图 9给出了MNIST数据集下InfoCatGAN在训练的不同阶段对应的生成效果。其中，L_I是公式(3)中的互信息下界，可以看到，随着隐变量c和生成数据$ \tilde{\boldsymbol{x}}$的互信息增加，生成的图片开始具有绑定效果，并且生成的图像越来越好。

对于InfoCatGAN在生成质量上的增益，本文参考文献[24]从互信息的角度给出一些直观解释。由式(5)、式(6)可知，生成器G的优化目标是最大化$ I(\tilde{\boldsymbol{x}} ; y)$和$ I(\tilde{\boldsymbol{x}} ; c)$, 这可以令虚假标签c和真实标签y对应；而半监督条件下判别器D的目标是最大化I(x; y)，以及最小化真实分布和预测分布之间的交叉熵$ -\mathrm{E}_{p(y \mid x)} \log p(c \mid \boldsymbol{x})$，进而使得真实标签y中的信息流入隐变量c。事实上，在半监督版本的InfoCatGAN中，本文就是采用c的后验概率p(c| ·)作为模型的预测值，从实验结果也可以看出虚假标签和真实标签是正确对应的(图 6(e))。换句话说，模型的优化目标变为I(c; x)和$ I(c;\mathit{\boldsymbol{\tilde x}})$。现假设：

1) $ \boldsymbol{x} \leftarrow c \longrightarrow \tilde{\boldsymbol{x}}$ : 其中→表示依赖性。这个假设来源于图像是由多个独立隐变量的相互作用生成的，实际中这些隐变量还包括噪声z，以及其他因素。为简单起见，这里假设只和隐变量c有关。

2) 初始$ I(\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\tilde x}}) = 0$ : 开始的时候，虚假数据和真实数据无关。

3) H(c)为常量：假设c的先验分布在训练过程中没有改变。

由文献[24]，H(c)可分解为

$ \begin{gathered} H(c)=I(c ; \boldsymbol{x})+I(c ; \tilde{\boldsymbol{x}})+H(c \mid \boldsymbol{x}, \tilde{\boldsymbol{x}})- \\ I(\boldsymbol{x} ; \tilde{\boldsymbol{x}})+I(\boldsymbol{x} ; \tilde{\boldsymbol{x}} \mid c) \end{gathered} $

由假设1)，

$ H(c)=I(c ; \boldsymbol{x})+I(c ; \tilde{\boldsymbol{x}})+H(c \mid \boldsymbol{x}, \tilde{\boldsymbol{x}})-I(\boldsymbol{x} ; \tilde{\boldsymbol{x}}) $

由假设3)，

$ \begin{aligned} &0=\Delta I(c ; \boldsymbol{x})+\Delta I(c ; \tilde{\boldsymbol{x}})+ \\ &\Delta H(c \mid \boldsymbol{x}, \tilde{\boldsymbol{x}})-\Delta I(\boldsymbol{x} ; \tilde{\boldsymbol{x}}) \end{aligned} $

其中Δ表示变化量。进一步得到以下两种情况：

$ \begin{aligned} \Delta I(c ; \boldsymbol{x})+\Delta I(c ; \tilde{\boldsymbol{x}}) & \geqslant-\Delta H(c \mid \boldsymbol{x}, \tilde{\boldsymbol{x}}) \Rightarrow \\ \Delta I(\boldsymbol{x} ; \tilde{\boldsymbol{x}}) & \geqslant 0, \\ \Delta I(c ; \boldsymbol{x})+\Delta I(c ; \tilde{\boldsymbol{x}}) & <-\Delta H(c \mid \boldsymbol{x}, \tilde{\boldsymbol{x}}) \Rightarrow \\ \Delta I(\boldsymbol{x} ; \tilde{\boldsymbol{x}}) & <0 . \end{aligned} $

注意到模型的训练目标是最大化两个互信息，所以上式左边一定为正值。由假设2)，初始时$ I(\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\tilde x}}) = 0$，如果第2种情况发生，则会导致$ I(\boldsymbol{x} ; \tilde{\boldsymbol{x}})$变为负值，而互信息是非负的，因此第2种情况不会发生。于是，增加I(c; x) 和$ I(\mathit{c};\mathit{\boldsymbol{\tilde x}})$会导致$ I(c ; \tilde{\boldsymbol{x}})$增加，这也就说明生成图片与真实图片更为接近，即模型的生成质量较好。

5 结论

本文首先提出InfoCatGAN模型，它通过优化隐变量和生成数据之间的互信息，能够获得更高的生成质量，同时可以通过调节正则系数实现生成质量和分类准确率的折中。为了同时兼顾二者，又提出C-InfoGAN模型。实验结果表明，InfoCatGAN可以在牺牲少量准确率的条件下提高图像的生成质量，而C-InfoGAN在一定程度上既可以生成高质量的图像，也能够达到可观的分类准确率，并且还可以调控生成图片的局部特征。未来的研究工作包括互信息项对于提高生成器生成效果的理论分析，如何进一步提高模型的分类准确率，以及针对复杂数据集的模型优化。