2. 中国科学院上海微系统与信息技术研究所,上海 200050;
3. 中国科学院大学,北京 100049
2. Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 200050, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
近年来,随着人工智能技术的不断发展,神经网络在身份验证[1]、金融服务[2]、自动驾驶[3]等和生命财产息息相关的领域已经得以成功应用,并且在这些应用中都扮演着至关重要的角色。尽管如今的神经网络模型精度越来越高,甚至有些已经超过人类,但是仍然存在被对抗样本攻击的隐患,这种情况不仅出现在图像识别[4]中,也出现在目标检测和语音识别中[5]。对抗攻击[4]是神经网络模型中常见的攻击方法,它通过给输入的图像添加人眼察觉不到的微小噪声扰动,使分类器错误分类,甚至可以根据设计的噪声扰动,输出攻击者想要的分类结果。如果这种攻击技术被犯罪份子用在关键场景[6],造成的后果难以想象。因此,神经网络模型安全性的研究具有很强的现实意义。
自从Szegedy等[7]于2014年第一次提出神经网络容易被攻击,学术界便致力于研究对应的防御方法。然而刚提出的防御方法很快就被新出现的攻击方法所攻破,起初Papernot等利用防御蒸馏法(defensive distillation)[8]来防御对抗样本。但是很快就被Carlini&Wagner(CW)攻击[9]所攻破。紧接着,许多研究者利用混淆梯度(obfuscated gradients)[10]作为防御手段,但是随即被Athalye等的向后传递可微分近似(backward pass differentiable approximation, BPDA)[10]所攻破。因此,很长一段时间内都是攻击者获胜,直到Madry等提出基于对抗训练(adversarial training, AT)的防御方法[11],它在CIFAR10测试集上,20步投影梯度下降(projected gradient descent, PGD)[11]攻击方法下仍保有47.0%的鲁棒准确度(robust accuracy)[12]。尽管随后Zhang等提出新的防御方法TRADES(tradeoff-inspired adversarial defense via surrogate-loss minimization)[13],将鲁棒准确度提升至56.6%,但是相比于不做攻击情况下90%以上的准确度,TRADES的防御性能仍然不够理想,实用价值不高。
最近,两种新颖的防御方法,双侧对抗训练法(bilateral adversarial training, BAT)[14]和特征打散法(feature scattering, FS)[15]被提出。它们的防御性能大大超越之前的防御方法,将鲁棒准确度猛地提升至68.9%,引起了学术界广泛的关注。然而,我们最近的工作显示BAT和FS所带来的革命性提升更像是海市蜃楼,在本文提出的新攻击方法下,BAT和FS的防御效果大打折扣。具体来说,在新攻击方法下,BAT和FS在CIFAR10数据集上准确度分别仅有20.8%和36.8%,明显弱于AT和TRADES,且在其他数据集上也观察到类似情况。因此,我们认为目前值得信赖的防御方法仍只有AT和TRADES。
评价模型防御性能的常见攻击方法有快速梯度符号法(fast gradient sign method, FGSM)[16]、CW和PGD,它们本质上都是基于图像标签的攻击方法。如前文所述,对于BAT和FS两种最先进的防御方法,这些攻击方法并不能正确反映出它们真实的防御性能。为此,本文提出一种新的攻击方法——基于特征的投影梯度法(feature based projected gradient descent, FB-PGD)。它通过迭代的方式给待攻击图像添加扰动,不断使待攻击图像和类别相异的目标图像的高维特征相似,从而产生欺骗分类器的对抗样本,这里高维特征指卷积神经网络中全局平均池化层的输出。FB-PGD与上述3种攻击方法主要区别有如下两点:
1) FB-PGD利用高维的、信息更丰富的特征设计损失函数,而上述3种攻击方法本质上利用低维的、信息贫瘠的图像标签设计攻击所需的损失函数。
2) FB-PGD利用选定的某一张目标图片作为攻击目标生成对抗样本,这里的对抗样本与选定的这张目标图片相关联。而上述3种攻击方法根据特定的类别标签生成对抗样本,这里的对抗样本与这个类别包含的大量图片相关联。
实验结果表明,本文提出的FB-PGD攻击方法对于BAT和FS两种最先进的防御方法,在多个数据集上均表现出远超FGSM、PGD和CW的攻击性能,攻击成功率较这3种攻击方法提升超过20%。
1 背景知识和相关工作 1.1 对抗样本对于图像分类任务来说,干净样本是那些从原始图像数据分布中采集出来的样本,对抗样本则是在干净样本基础上经过精心设计的让分类器分类错误的样本。精心设计指的是给干净样本添加人眼察觉不到微小扰动,人无法区分干净样本和对应的对抗样本。图 1展示了干净样本和使用快速梯度符号法生成的对抗样本,最左边图片表示干净样本,中间图片表示通过快速梯度符号法产生的微小噪声扰动,最右边的图片表示最终生成的对抗样本。图中干净样本被分类器以57.7%的概率识别为熊猫,而添加扰动的对抗样本则被分类器以99.3%的概率错误分类为长臂猿。从计算机的角度来说,干净样本上的噪声扰动强弱需要特定的度量标准去描述,研究者们通常使用如下3种度量标准来模拟人的感官:L0、L2和L∞。上述3种扰动度量标准其实是Lp范数的特殊形式,对于样本x有
| $ {\left\| x \right\|_p} = {\left( {\sum\limits_{i = 1}^n {{{\left| {{x_i}} \right|}^p}} } \right)^{\frac{1}{p}}}. $ | (1) |

|
Download:
|
| 图 1 快速梯度符号法生成对抗样本的示意图[16] Fig. 1 Adversarial examples generated by fast gradient sign method[16] | |
Goodfellow等最早发现神经网络中存在对抗样本[16],之后研究者提出各种不同的方法生成对抗样本,其中绝大多数的攻击方法是基于梯度优化生成对抗样本,其本质上属于基于梯度的局部搜索,通过梯度方向在干净样本的邻域内搜索可能存在的对抗样本。能否找到合适的梯度方向是攻击成功与否的关键。本文提出的FB-PGD攻击方法和常见的攻击方法类似,也是基于梯度优化的方法,不同的是FB-PGD针对某一具体图像生成对抗扰动,而常见的攻击方法针对某一特定类生成对抗扰动。在损失函数的设计上也与常见的方法不同,FB-PGD利用神经网络中中间层输出的高维特征设计损失函数,而常见攻击方法采用低维的图像标签信息设计损失函数。直观上讲,上述两点创新使FB-PGD更容易找到精准的梯度方向,利于更好地生成对抗样本。本文用如下3种攻击方法与FB-PGD相比较,说明FB-PGD的攻击性能更强。
1.2.1 快速梯度符号法FGSMFGSM[16]属于L∞范数限制下的对抗攻击方法,通过在干净图像的L∞邻域内找到对抗样本使分类器错误分类,FGSM定义了损失函数L(x, y)表示输入的干净样本x被分类器分类成真实标签y的损失,攻击过程中通过最大化这个损失函数来生成对抗样本。具体来说,FGSM通过反向传播得到损失函数对于输入x的梯度,然后对于输入图像上的每个像素加上梯度方向ε大小的扰动,进而得到对抗样本,可以表示为
| $ x' = x + \varepsilon \cdot {\rm{sign}}\left( {{\nabla _x}L\left( {x, {\rm{ }}y} \right)} \right). $ | (2) |
当扰动步长ε增加时,对抗样本x′的扰动大小增加,攻击成功率增加。FGSM的优点是可以快速生成对抗样本,但是不能保证生成的对抗样本一定能被分类器分类错误。
1.2.2 投影梯度下降法PGDPGD[12]根据不同范数设置可以生成全部3种范数限制下的对抗样本。这里用基于L∞范数的投影梯度法说明该攻击方法的思路。基于L∞范数的PGD可以看作是FGSM的一种扩展,该对抗攻击方法在攻击阶段执行多次的FGSM攻击,每次用较小的扰动α而不是ε,并且每次攻击之后把对抗样本投影回干净样本的L∞邻域内,即每次攻击生成的对抗样本x′i满足‖x′i-x‖∞≤ε。可以表示为
| $ {x'_{i + 1}} = {\rm{cli}}{{\rm{p}}_{x, \varepsilon }}\left\{ {{{x'}_i} + {\rm{ }}\alpha \cdot {\rm{sign}}\left( {{\nabla _{{{x'}_i}}}L\left( {{{x'}_i}, y} \right)} \right)} \right\}. $ | (3) |
其中:i为PGD的步数,截断函数clip(·)确保生成的对抗样本满足L∞范数约束和图像本身的像素值值域约束。与FGSM类似,PGD也不能保证生成对抗样本一定能攻击成功,但是相较于FGSM攻击成功率更高,且生成的对抗样本对于干净的样本来说,修改幅度小。从式(2)和式(3)可以看出FGSM和PGD都是根据图像标签设计损失函数,本文后续实验中PGD方法采用此方案。
1.2.3 CW攻击方法CW攻击方法[9]是目前最先进的攻击方法,该攻击方法根据不同范数设置可以生成全部3种范数限制下的对抗样本。这里用L∞范数限制下的攻击方法说明该攻击方法的大致思路。该攻击方法主要优化如下优化目标:
| $ \begin{array}{c} x' = x + \delta , \\ \mathop {{\rm{min}}}\limits_\delta {\left\| \delta \right\|_\infty } + c \cdot f\left( {x'} \right), \\ {\rm{s}}{\rm{.t}}.x' \in {\left[ {0, 1} \right]^n}, \\ f\left( {x'} \right) = {\rm{max}}\left( {{\rm{max}}\left\{ {Z{{\left( {x'} \right)}_i}:i \ne t} \right\} - Z{{\left( {x'} \right)}_t}, - \kappa } \right). \end{array} $ | (4) |
对于干净样本x,该攻击方法希望找到一个在约定范数内尽可能小的扰动δ,使得生成的对抗样本x′成功欺骗分类器,且满足RGB空间像素值域范围(这里[0, 1]是归一化的像素值)。其中c是一个超参数,用来权衡两个损失函数之间的关系,作者使用二分查找找出合适的c值。f(·)是作者设计的损失函数,其中Z(·) 表示神经网络中Softmax函数前一层的输出结果,即逻辑值向量(Logits)。对于干净的样本来说,逻辑值向量中最大值的下标对应的就是正确的类别(如果分类正确),现在将想要攻击的目标类别t所对应的逻辑值记为Z(x′)t,将未攻击成功时预测的最大的逻辑值(对应类别不同于t)记为max{Z(x′)i: i≠t},通过优化使得max{Z(x′)i: i≠t}-Z(x′)t变小,抑制正确类的逻辑值同时提升目标类别t的逻辑值。公式中的κ表示置信度,κ值越大,意味着将x′分为t类的可能性越大,同时添加的扰动也越大。尽管CW攻击不直接利用图像标签设计损失函数,但是利用标签对应的逻辑值。因此,本质上还是基于标签设计损失函数。
该方法的攻击成功率高,但是计算量过大导致对抗样本生成速度慢,一般采用简化版本[11, 15]。即套用PGD攻击方法的框架,其中式(3)中的损失函数L(x′i, y)替换为f(·),本文后续实验中CW方法采用此方案。
1.3 防御方法介绍自从Madry等提出AT方法[11]之后,其他研究者提出了各种不同的改进方法,但都提升有限,之前改进效果最好的是ZHANG等提出的TRADES,但在CIFAR10上也仅提升了9.6%[13]。最近提出的BAT和FS提升效果惊人,分别提升了16.7%[14]和21.9%[15],但在本文提出的攻击方法FB-PGD上,BAT与FS的防御性能变得很差,甚至不如AT。本文主要实验了如下3种防御方法,来说明FB-PGD的攻击性能优异。
1.3.1 对抗训练法AT如何防御对抗样本,一个直观的想法是把对抗样本加入训练集去训练分类器,训练时使用正确的标签,以此让分类器能够像对待干净样本一样正确分类对抗样本,该方法即为AT法[12]。Madry等用PGD生成对抗样本来训练分类器,数学上来说,就是解决一个min-max优化问题,公式如下
| $ \mathop {{\rm{min}}}\limits_\theta {{\mathbb{E}}_{\left( {x, y} \right) \sim D}}\left[ {\mathop {{\rm{max}}}\limits_{{{\left\| \delta \right\|}_\infty } \le \varepsilon } L\left( {\theta , x + \delta , y} \right)} \right]. $ | (5) |
其中: max优化函数的优化目标即1.2.2节中的投影梯度法,δ表示添加的扰动,通过优化在‖δ‖∞≤ε范围内找到使损失函数L(·)值最大的扰动,得到对抗样本,并用对抗样本训练模型参数θ。该方法原理简单,易于实现。
1.3.2 双侧对抗训练法BATBAT[14]是在AT基础上改进得到,与AT不同的是,BAT在做对抗训练的时候不但给图像添加扰动,同时也给独热标签(one-hot label)添加扰动,这点类似于标签平滑[17](label smoothing)。该方法在给图像生成扰动的时候,也是通过投影梯度法得到对抗扰动。在给标签添加扰动的时候,一方面稍微抑制正确标签的概率值,另一方面根据其余各错误标签的梯度值大小,稍微提升错误标签的概率值。最后利用生成的对抗样本和添加扰动的标签训练分类器。
1.3.3 特征打散法FSFS[15]也是在对AT基础上改进得到,对AT通过最大化输入样本与正确标签之间的交叉熵损失函数生成扰动,进而得到对抗训练所需的对抗样本。而FS通过无监督的方式生成对抗训练所需的对抗样本,即通过最大化干净样本与对应的对抗样本之间逻辑值向量的最优传输距离(optimal transport distance)[15]生成扰动。作者认为对AT中对抗扰动的生成过度依赖决策边界(即标签)会导致标签泄露(label leaking),即生成的对抗样本聚集在决策边界附近,当用这些偏见严重的对抗样本训练分类器后,会导致分类器泛化能力变差,防御效果也随之变差。而采用无监督的方式,在生成对抗样本时,考虑样本之间的联系可以使生成的对抗样本更合理地分布在整个样本空间中,继而利用这些对抗样本训练出来的防御模型,防御效果也会更好。
2 FB-PGD攻击方法 2.1 攻击原理对于图像分类任务下神经网络为什么易受攻击,很多研究者认为是神经网络更偏向于关注图像上的非鲁棒特征[18]、纹理特征[19]和低频特征[20],这3种特征本质上一样。如何提取目标图像上能被神经网络所关注的非鲁棒特征并在待攻击图像上生成它们显然是攻击成功与否的关键。FB-PGD中使用的特征,即经过全局平均池化层输出的特征,包含了图像经过卷积提取出来的丰富信息,被广泛应用于人脸识别和验证[21]。本文提出的FB-PGD攻击受上述工作启发,用图像的特征而不是标签信息来生成扰动,在BAT和FS两种最先进的防御方法上表现出了很强的攻击性能。
目前常用的攻击方法有FGSM,PGD和CW,其中FGSM和PGD利用图像标签通过最大化损失函数生成对抗样本,CW则利用对应标签的逻辑值构造出新的损失函数,通过抑制正确类的逻辑值同时提升目标类的逻辑值生成对抗样本。这3种攻击方法在构造损失函数时都直接或者间接利用了非常低维的图像标签,这些图像标签显然丢失了图像本身的许多信息。根据Ilyas等的非鲁棒特征理论(non-robust features)[18],图像本身包含鲁棒特征和非鲁棒特征。卷积神经网络倾向于识别图像上的非鲁棒特征,而人眼倾向于感知图像上的鲁棒特征并忽视非鲁棒特征。正是这些人眼不易察觉但是神经网络偏爱的非鲁棒特征导致了对抗样本的产生。能否在待攻击的图像上生成其他类别图像的非鲁棒特征决定了攻击的成功与否。因此,直觉上来看,如果在攻击阶段利用更多的目标图像信息,或许能更提高攻击成功率。
2.2 FB-PGD攻击介绍受前述猜想启发,为了利用目标图像更多的信息,本文提出一种基于高维特征的图像对抗攻击算法FB-PGD。算法具体流程如图 2所示。

|
Download:
|
| 图 2 FB-PGD攻击算法示意图 Fig. 2 Feature based projected gradient descent attack pipeline | |
图 2中首先根据待攻击图像x(标签为y),选取一张目标图像xtar,其真实标签ytar与y不同。接着在待攻击图像L∞范数约束的邻域内随机找到一张图像当作初始化的对抗图像x′0。
| $ {\left\| {{{x'}_0} - x} \right\|_\infty } \le \varepsilon . $ | (6) |
然后使初始化的对抗图像的特征
| $ {D_c}\left( {{{\mathcal{F}}_{{{x'}_0}}}, {{\mathcal{F}}_{{x_{{\rm{tar}}}}}}} \right) = {\rm{ }}1 - {S_c}\left( {{\mathcal{F}}\left( {{{x'}_0}} \right), {\mathcal{F}}\left( {{x_{{\rm{tar}}}}} \right)} \right). $ | (7) |
其中:Sc(·)表示2个向量之间的余弦相似度。最后,将生成的扰动添加到初始化的对抗图像上,得到更新完的对抗图像x′1。至此,第一次攻击迭代结束。迭代公式如下
| $ \begin{array}{l} \delta = - \alpha \cdot {\rm{sign}}\left( {{\nabla _{{{x'}_t}}}{D_c}\left. {\left( {{{\mathcal{F}}_{{{x'}_t}}}, {{\mathcal{F}}_{{x_{{\rm{tar}}}}}}} \right)} \right]} \right), \\ {{x'}_{t + 1}} = {\rm{cli}}{{\rm{p}}_{x, \varepsilon }}\left\{ {{{x'}_t} + \delta } \right\}. \end{array} $ | (8) |
其中:sign(·)为符号函数,α为每次添加扰动的步长,截断函数clip{·}确保生成的对抗样本满足L∞范数约束和图像本身的像素值值域约束。
算法伪代码如下:
算法1 FB-PGD算法
输入:特征提取模型
输出:对抗样本x′
1: 在邻域内选取随机一点作为初始化
x′0← x+uniform_noise(-ε, ε);
2: 提取目标图像的特征:
3: for t=0 to T-1 do; //T步迭代攻击
4:
5: x′t+1←x′t-α·sign(▽x′tDc);
6: x′t+1←min(max(x′t+1, x-ε), x+ε);
7: x′t+1←clip(x′t+1, min=0, max=255);
8: end for
9: x′←x′T;
10: return x′.
2.3 算法优化由于在攻击阶段,目标图像的选择范围很广,可以是除了类别为正确类之外的所有图像。如果每次攻击只选用一张目标图像,攻击效率将会很低。为了有效地利用显卡并行计算的功能达到加速攻击过程的效果。实际攻击阶段在所有待选的目标图像里随机采样N张图像{xtar1, …, xtarN},并将待攻击图像复制N份{x1, …, xN},每次迭代同时攻击N对图像{(x1, xtar1), …, (xN, xtarN)},本文实验中N取100。此外,同样为了加速攻击过程,对于N对图像,每次迭代结束,检查是否存在已经攻击成功的一对或多对图像,若有则结束本次攻击,否则继续迭代,直至达到预设的最大迭代次数T。
3 实验与分析 3.1 数据集介绍本文评测的数据集有CIFAR10[22]、SVHN[23]和CIFAR100[22]。CIFAR10数据集有10个类别,5万张训练图像(每个类5千张)和1万张测试图像。SVNH数据集取自街景门牌号码,10个阿拉伯数字对应10个类别,包含73 257张训练图像和26 032张测试图像。CIFAR100数据集作为比CIFAR10更有挑战性的数据集,不仅类别数是CIFAR10的10倍,而且每个类的样本数只有CIFAR10的1/10。CIFAR100有100个类别,5万张训练图像和1万张测试图像。本文中攻击算法的评测皆是在3个数据集的测试集上进行。
3.2 实验细节和评价指标为了公平地比较几种攻击方法的性能,本次实验中防御模型的网络结构都选用Wide ResNet(WRN28-10)[24],详细结构如表 1所示。表中k表示网络的宽度因子,本次实验k为10。N表示块的数量,输出大小(CHW)表示对应层输出特征张量的通道数(C)、宽(W)和高(H)。防御模型训练过程中超参设置与BAT和FS的论文中一致,共训练200个epoch。对于数据集CIFAR10和CIFAR100初始学习率为0.1,分别在60和90个epoch处衰减为之前的1/10;对于数据集SVHN初始学习率为0.01,同样在60和90个epoch衰减为之前的1/10。对于BAT防御模型,采用R-MC-LA(random start and most confusing targeted attack with label adversarial)[14]结合一步对抗训练得到,其中因子β=9。实验中共训练了4种防御模型,包含原始的仅使用干净样本训练的标准模型(Standard)和Madry等的对抗训练模型(Madry),以及基于BAT和FS防御方法训练的模型。实验中比较4种模型在干净样本和不同攻击方法下的分类准确度,这里分别简称为原始准确度和鲁棒准确度。鲁棒准确度越低,说明攻击成功率越高,攻击性能越好。
|
|
表 1 Wide ResNet结构示意图 Table 1 The architecture of Wide ResNet |
攻击方面,本次实验选择FGSM、PGD和CW共3种攻击方法与FB-PGD作对比。如不额外说明,默认对于单步攻击FGSM,攻击步长与扰动上限相等α=ε=8;对于多步攻击的PGD、CW和FB-PGD,攻击步长α=2,扰动上限ε=8,迭代次数T=20。
3.3 实验结果分析 3.3.1 不同扰动上限通过固定其他参数,仅选取不同的扰动上限,对比PGD、CW和FB-PGD这3种攻击方法在相同防御模型上的攻击成功率。具体来说,选取7种不同的扰动上限ε={2, 4, 6, 8, 12, 16, 20}。攻击阶段,对于不同的扰动上限,实验中采用固定的攻击参数,其中攻击步长α为2,最大迭代次数T为20。实验结果如图 3(a)所示。图中反映了在数据集CIFAR10上,3种不同攻击算法在防御模型FS上的攻击效果,其中纵坐标Accuracy表示防御模型FS在攻击算法下的鲁棒准确度。从图中可以看出,横向上,随着扰动上限的不断增大,FS防御模型在3种不同攻击算法下的鲁棒准确度随之降低。这表明,随着扰动上限的增加,FB-PGD与PGD和CW表现出相似的性质,即在FS上的攻击性能增加,符合攻击强度与扰动上限成正相关这一准则[25]。纵向上,对于相同的扰动上限,防御模型FS在FB-PGD攻击下的鲁棒准确度始终远低于PGD和CW,表明FB-PGD攻击算法在防御模型FS上的攻击性能明显优于PGD和CW。同样的实验结果也出现在BAT上,如图 3(b)所示。所以,对于FS和BAT两种最先进的防御方法,在不同的扰动上限下,FB-PGD攻击性能均强于PGD和CW。

|
Download:
|
| 图 3 不同扰动上限的结果 Fig. 3 The results in different attack budgets | |
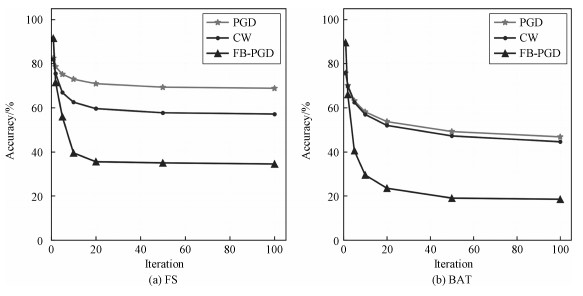
通过固定其他参数,仅选取不同的最大攻击步数,对比PGD、CW和FB-PGD这3种攻击方法在相同防御模型上的攻击成功率。具体来说,选取7个不同的最大攻击步数T={1, 2, 5, 10, 20, 50, 100}进行实验。攻击参数设置上,所有攻击选用相同的扰动上限ε=8和攻击步长α=2。在CIFAR10数据集上,3种对抗攻击算法在不同攻击步数设置下,攻击FS防御模型的的结果如图 4(a)所示。
|
Download:
|
| 图 4 不同攻击步数的结果 Fig. 4 The results in different attack iterations | |
从图 4(a)可以看出,横向上,随着攻击步数的增加,3种攻击方法均表现出相同变化情况。在最大攻击步数小于20步的情况下,FS防御模型在3种攻击方法下的鲁棒准确度急剧下降,而在大于20步的情况下,鲁棒准确度趋于收敛。纵向上,当最大攻击步数大于等于2步时,可以观察到FB-PGD的攻击性能比PGD和CW表现出绝对优势。当最大步数小于2步时FB-PGD却弱于PGD和CW,这一反常现象是由于FB-PGD利用高维的特征向量(本实验中特征向量的元素数量为640),它比PGD和CW利用的标签信息(元素数量不超过2)维度更高,需要稍多一点的迭代步数去优化。在防御模型BAT上的实验结果也与FS上的一致,如图 4(b)所示。所以,对于FS和BAT两种最先进的防御方法,在攻击步数不少于1的情况下,FB-PGD攻击性能均强于PGD和CW。
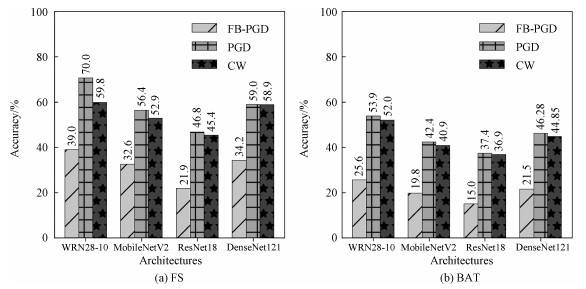
3.3.3 不同网络结构通过固定其他参数,仅选取不同的网络结构,对比PGD、CW和FB-PGD这3种攻击方法在相同防御方法上的攻击成功率。具体来说,选取除WRN28-10外3种不同的网络结构进行实验,分别为MobileNetV2[26]、ResNet18[27]和DenseNet121[28]。攻击参数设置上,所有攻击选用相同的扰动上限ε=8、攻击步长α=2和最大迭代次数T=20。在CIFAR10数据集上,3种对抗攻击方法攻击利用不同网络结构训练的FS防御模型,攻击结果如图 5(a)所示。从图中可以看出,FB-PGD攻击方法相比于PGD和CW,在4种不同网络结构训练出的FS防御模型上,均取得最低的鲁棒准确度。这表明FB-PGD在不同网络结构训练的FS防御模型上,攻击性能均明显强于PGD和CW,同样的实验结果也出现在利用不同网络结构训练的BAT防御模型上,如图 5 (b)所示。因此,对于不同的网络结构下的FS和BAT,FB-PGD攻击性能也均强于PGD和CW。
|
Download:
|
| 图 5 不同网络结构的结果 Fig. 5 The results in different network architectures | |
前3个小节主要表述在CIFAR10数据集上,对于FS和BAT,FB-PGD比PGD和CW攻击性能强。本小节分析在更多的数据集和防御方法下,FB-PGD的攻击性能。通过在CIFAR10、CIFAR100和SVHN这3个不同数据集上,比较FB-PGD与常见攻击算法在7种不同模型上的攻击性能,7种模型分别为标准训练模型(Standard)、基于交叉熵损失函数的PGD对抗训练防御模型(Madry)、基于FB-PGD对抗训练的防御模型(FB-PGD-D)、改进的对抗训练防御模型(TRADES)、非对抗训练防御模型(guided complement entropy, GCE)[29],以及基于FS和BAT训练的防御模型。实验结果如表 2所示。
|
|
表 2 不同攻击方法攻击不同防御模型的结果 Table 2 The results of different attack methods against different defense models |
表 2中的结果为特定攻击下对应防御模型的准确度。其中Clean表示不做任何攻击,对应栏为每个模型的原始准确度。PGD20和PGD100分别指20步和100步的PGD攻击,对应栏为每个模型的鲁棒准确度,鲁棒准确度越低说明对应栏的攻击方法在对应列的防御模型上攻击性能越强,CW20等同理。表格被2条竖线分为3栏,每一栏里,每行中最好的攻击结果用黑体标出(攻击成功率最高),δ列中结果由左侧栏里的黑体数字减去中间栏里的黑体数字得出,表示FB-PGD相对于左侧最强攻击方法能提升多少攻击成功率,数字越大表示FB-PGD比其他攻击方法攻击性能越强。
从表 2可以看出,本文提出的FB-PGD攻击算法在标准训练的模型(Standard)上攻击性能与PGD和CW相似,在3个数据集上几乎能完全攻击成功。且FB-PGD攻击算法在Madry、TRADES和FB-PGD-D等3种基于对抗训练的防御模型上也表现良好,在3个不同的数据集上攻击效果与PGD和CW几乎持平。从δ列可以看出,FB-PGD相比于PGD和CW两种攻击方法,它们的攻击性能在Madry、TRADES和FB-PGD-D上差距不超过1%。在非基于对抗训练的在防御模型GCE上,同样可以观察到FB-PGD与PGD和CW有相近的攻击性能。
此外,从δ列中结果可以看出,FB-PGD对于BAT和FS这两种最先进的防御方法,攻击性能显著超过FGSM、PGD和CW等3种攻击方法。具体来说,在3个数据集上,对于BAT和FS防御方法,FB-PGD比FGSM、PGD和CW,攻击成功率都至少提高20%。综上所述,在不同数据集和不同防御模型下,实验结果显示FB-PGD是一个比FGSM、PGD和CW攻击性能更强的攻击方法。它不仅在标准训练的模型、Madry、FB-PGD-D、TRADES和GCE防御模型上攻击性能表现优异,而且对于最先进的FS和BAT防御方法,比FGSM、PGD和CW的攻击成功率提升超过20%。因此,FB-PGD可以成为检验防御方法的新基准。
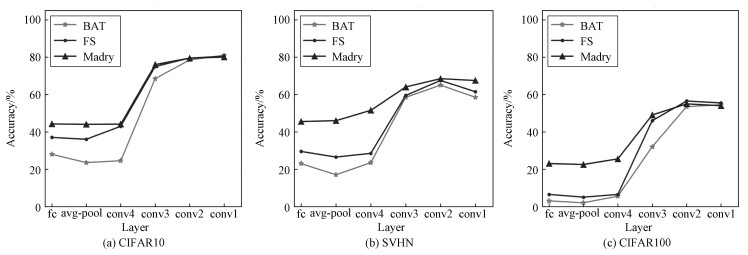
3.4 不同位置的特征层选取WRN28-10上6个不同位置的输出特征,讨论FB-PGD在不同特征层上的攻击性能,如表 1所示,6个位置分别位于第1~4层卷积层(conv1~4)、全局平均池化层(avg-pool)和最后分类的全联接层(fc)。攻击阶段,对于不同层,实验中采用固定的攻击参数,其中扰动上限ε为8,攻击步长α为2,最大迭代次数T为20。在CIFAR10上,对BAT、FS和Madry这3种防御方法的攻击结果如图 6(a)所示。从图中可以看出,曲线大致呈“S”型,表明随着选取的特征层越来越靠近WRN28-10的输入层,特征维度升高,FB-PGD攻击方法在BAT、FS和Madry这3种不同的防御方法上都表现出攻击成功率下降的趋势(鲁棒准确度上升)。同时,在左端曲线趋于平缓,这说明FB-PGD在最靠近网络输出层的3层(fc、avg-pool和conv4)上有着相近的攻击性能。当FB-PGD特征层位置选取为全局平均池化层(avg-pool)时,此时3种防御方法的鲁棒准确度皆最低。此外,在SVHN和CIFAR100 2个数据集也进行了相同的实验,均观察到与在CIFAR10数据集上大致类似的现象,如图 6(b)和6(c)所示。因此,当特征层选取在全局平均池化层时,FB-PGD攻击性能最强。
|
Download:
|
| 图 6 不同特征层的结果 Fig. 6 The results in different layers | |
本文提出一种全新的基于高维特征的图像对抗攻击算法FB-PGD,它通过给待攻击图像添加扰动使待攻击图像与目标图像的高维特征相似,从而生成对抗样本。本文介绍了该算法的原理和具体流程,还给出了该算法的优化版本。实验结果表明,该攻击算法不仅在标准训练的模型和Madry等的防御模型上攻击性能优异,而且对于最先进的FS和BAT两种防御方法,在不同扰动上限、不同攻击迭代次数和不同网络结构下,均表现出优于FGSM、PGD和CW的攻击性能,且在惯常的攻击参数下,攻击成功率较这3种攻击方法提升超过20%。因此,FB-PGD可以成为检验防御方法性能的新基准。
| [1] |
杨建斌, 张卫强, 刘加. 深度神经网络自适应中基于身份认证向量的归一化方法[J]. 中国科学院大学学报, 2017, 34(5): 633-639. Doi:10.7523/j.issn.2095-6134.2017.05.014 |
| [2] |
黄胜, 王博博, 朱菁. 基于文档结构与深度学习的金融公告信息抽取[J]. 计算机工程与设计, 2020, 41(1): 115-121. Doi:10.16208/j.issn1000-7024.2020.01.019 |
| [3] |
Yurtsever E, Lambert J, Carballo A, et al. A survey of autonomous driving: common practices and emerging technologies[J]. IEEE Access, 2020, 8: 58443-58469. Doi:10.1109/ACCESS.2020.2983149 |
| [4] |
Yuan X Y, He P, Zhu Q L, et al. Adversarial examples: attacks and defenses for deep learning[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(9): 2805-2824. Doi:10.1109/TNNLS.2018.2886017 |
| [5] |
Carlini N, Wagner D. Audio adversarial examples: Targeted attacks on speech-to-text[C]//2018 IEEE Security and Privacy Workshops (SPW). May 24, 2018, San Francisco, CA, USA. IEEE, 2018: 1-7. DOI: 10.1109/SPW.2018.00009.
|
| [6] |
Eykholt K, Evtimov I, Fernandes E, et al. Robust physical-world attacks on deep learning visual classification[C]// 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. June 18-23, Salt Lake City, UT, USA. 2018: 1625-1634. DOI: 10.1109/CVPR.2018.00175.
|
| [7] |
Szegedy C, Zaremba W, Sutskever I, et al. Intriguing properties of neural networks[EB/OL]. arXiv: 1312.6199 (2014-02-19)[2020-04-22]. https://arxiv.org/abs/1312.6199.
|
| [8] |
Papernot N, McDaniel P, Wu X, et al. Distillation as a defense to adversarial perturbations against deep neural networks[C]//2016 IEEE Symposium on Security and Privacy (SP). May 22-26, 2016, San Jose, CA, USA. IEEE, 2016: 582-597. DOI: 10.1109/SP.2016.41.
|
| [9] |
Carlini N, Wagner D. Towards evaluating the robustness of neural networks[C]//2017 IEEE Symposium on Security and Privacy (SP). May 22-26, San Jose, CA, USA. IEEE, 2017: 39-57. DOI: 10.1109/SP.2017.49.
|
| [10] |
Athalye A, Carlini N, Wagner D. Obfuscated gradients give a false sense of security: circumventing defenses to adversarial examples[EB/OL]. arXiv: 1802.00420(2018-07-31)[2020-04-22]. https://arxiv.org/abs/1802.00420.
|
| [11] |
Madry A, Makelov A, Schmidt L, et al. Towards deep learning models resistant to adversarial attacks[EB/OL]. arXiv: 1706.06083(2019-09-04)[2020-04-22]. https://avxiv.org/abs/1706.06083.
|
| [12] |
Tsipras D, Santurkar S, Engstrom L, et al. Robustness may be at odds with accuracy[C]//International Conference on Learning Representations. 2019.
|
| [13] |
Zhang H Y, Yu Y D, Jiao J, et al. Theoretically principled trade-off between robustness and accuracy[C]//International Conference on Machine Learning. 2019: 7472-7482.
|
| [14] |
Wang J Y, Zhang H C. Bilateral adversarial training: Towards fast training of more robust models against adversarial attacks[C]//2019 IEEE/CVE International Conference on Computer Vision(ICCV). October 27-November 2, 2019, Seoul, Korea(South). IEEE, 2019: 6628-6637. DOI: 10.1109/ICCV.2019.00673.
|
| [15] |
Zhang H C, Wang J Y. Defense against adversarial attacks using feature scattering-based adversarial training[C]// Wallach H, Larochelle H, Beygelzimer A, et al. Advances in Neural Information Processing Systems(NIPS 2019). 2019: 1829-1839.
|
| [16] |
Goodfellow I J, Shlens J, Szegedy C. Explaining and harnessing adversarial examples[C]//3rd International Conference on Learning Representations, ICLR 2015-Conference Track Proceedings. 2015: 1000-2010.
|
| [17] |
Müller R, Kornblith S, Hinton G E. When does label smoothing help?[C]//Advances in Neural Information Processing Systems(NIPS 2019). 2019: 4696-4705.
|
| [18] |
Ilyas A, Santurkar S, Tsipras D, et al. Adversarial examples are not bugs, they are features[C]//Advances in Neural Information Processing Systems(NIPS 2019). 2019: 125-136.
|
| [19] |
Geirhos R, Rubisch P, Michaelis C, et al. ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustness[EB/OL]. arXiv: 1811.12231(2019-01-14)[2020-04-22]. https://arxiv.org/abs/1811.12231.
|
| [20] |
Rahaman N, Baratin A, Arpit D, et al. On the spectral bias of neural networks[EB/OL]. arXiv: 1806.08734(2019-05-31)[2020-04-22]. https://arxiv.org/abs/1806.08734.
|
| [21] |
Parkhi O M, Vedaldi A, Zisserman A. Deep face recognition[C]//Proceedings of the British Machine Vision Conference (BMVC 2015), Swansea. British Machine Vision Association, 2015: 41.1-41.12. DOI: 10.5244/c.29.41.
|
| [22] |
Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images[J]. Handbook of Systemic Autoimmune Diseases, 2009, 1(4): 1-10. |
| [23] |
Netzer, Y, Wang, T, Coates, A, et al. Reading digits in natural images with unsupervised feature learning[C]//NIPS Workshop on Deep Learning and Unsupervised Feature Learning, 2011: 5-15.
|
| [24] |
Zagoruyko S, Komodakis N. Wide residual networks[C]//Proceedings of the British Machine Vision Conference (BMVC 2016), York, UK. British Machine Vision Association, 2016: 87.1-87.12. DOI: 10.5244/c.30.87.
|
| [25] |
Carlini N, Athalye A, Papernot N, et al. On evaluating adversarial robustness[EB/OL]. arXiv: 1902.06705(2019-02-20)[2020-04-22]. https://arxiv.org/abs/1902.06705.
|
| [26] |
Sandler M, Howard A, Zhu M, et al. Mobilenetv2: Inverted residuals and linear bottlenecks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. June 18-23, 2018, Salt Lake City, UT, USA. IEEE, 2018: 4510-4520. DOI: 10.1109/CPVR.2018.00474.
|
| [27] |
He K M, Zhang X Y, Ren S Q, et al. Deep residual learning for image recognition[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. June 27-30, 2016, Las Vegas, NV, USA. IEEE, 2016: 770-778. DOI: 10.1109/CPVR.2016.90.
|
| [28] |
Huang G, Liu Z, van der Maaten L, et al. Densely connected convolutional networks[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. July 21-26, 2017, Honolulu, HI, USA. IEEE, 2017: 2261-2269. DOI: 10.1109/CPVR.2017.243.
|
| [29] |
Chen H Y, Liang J H, Chang S C, et al. Improving adversarial robustness via guided complement entropy[C]//2019 IEEE/CVF International Conference on Computer Vision(ICCV). October 27-November 2, 2019, Seoul, Korea (South). IEEE, 2019: 4880-4888. DOI: 10.1109/ICCV.2019.00498.
|
 2022, Vol. 39
2022, Vol. 39 


