大数据时代为我们带来了海量的个体信息,这些个体间的联系构成了纵横交错的网络数据。网络数据涵盖了社交网络[1]、在线营销[2]、医疗数据[3]以及气候分析[4]等一系列当代应用。这些数据通常具有成千上万的维度,这就使得高维数据的作用越来越突出。研究这些高维网络数据间的联系具有非常实际的意义。图模型可以作为研究变量条件关联的一种工具[5]。在图模型中,图模型的条件独立性可以由它的精度(逆协方差)矩阵来确定[6]。在高斯图模型中,图模型的条件独立结构完全由精度矩阵的零元素来确定[7]。因此,挖掘网络数据变量间联系也就是恢复图模型的精度矩阵。
然而由于高维数据的出现,往往会出现变量大于样本容量的情形。在这种情况下,用样本协方差矩阵的逆来估计精度矩阵不再可行。即使可行,求解一个高维矩阵的逆,在内存和时间上的成本也是巨大的。这就使得高维图模型精度矩阵的求解成为各学者研究的热点。当前的研究主要集中在精度矩阵的点估计上[8-15]。我们知道,通过置信区间来评估估计量的精度是很重要的[16-17]。然而由于现有估计量抽样分布的复杂性,目前对高维稀疏精度矩阵的置信区间还很少涉及。
近年来,对于高维统计推断的研究主要转向高维线性和广义线性模型回归系数上[18-21]。特别是van de Geer等[19]对Lasso估计量进行KKT(Karush-Kuhn-Tucker)反转得到高维线性回归系数的渐近正态统计量。后来他们又将该方法推广到广义线性模型中。遵循文献[19]的思想,Jankov和van de Geer等[22]将这种消除惩罚偏差的思想运用到精度矩阵的统计推断中。他们通过对Glasso(graphical Lasso)[11]估计量进行KKT反转得到De-Glasso(De-sparsified graphical Lasso)统计量,并给出渐近正态性的理论保证,进而得到精度矩阵各个元素的置信区间。遵循这种KKT反转的思想,文献[23-24]都通过对精度矩阵点估计的似然函数KKT反转得到不同设定下的渐近正态统计量。还有一类统计推断方法是Ren等[14]提出的ANT(asymptotically normal estimation and then do thresholding)方法,它是每2个变量对剩余变量进行回归得到一个渐近正态估计量。
本文研究发现,置信区间的计算成本主要来自于精度矩阵的点估计。上述提出的第1类置信区间由于各自点估计具有复杂的似然函数以及需选择调优参数而计算不有效。第2类置信区间由于ANT点估计需要进行O(p2)次scaled Lasso回归而使得计算成本加大。当维度适中时,两类方法都可以有效地计算精度矩阵的置信区间,然而当维度逐渐增加时,上述方法的计算效率开始变低。为解决上述问题,本文受文献[22]渐近正态统计量的启发提出De-ISEE统计量,并给出对应元素的置信区间。
本文提出的De-ISEE统计量是ISEE点估计的简单运算,且ISEE估计量有成熟的算法,这使得De-ISEE统计量易于计算。相比较其他方法,De-ISEE方法由于ISEE点估计具有可伸缩、易调参等优点可处理超高维精度矩阵。从仿真实验中可以看出,De-ISEE方法得出的置信区间不仅覆盖率更接近于理想覆盖率,而且计算高效。并且本文将De-ISEE方法运用到核黄素数据集以及前列腺肿瘤基因表达数据集,发现De-ISEE方法很好地恢复了变量间的联系,这可作为研究基因学的一种辅助工具。
1 精度矩阵的置信区间 1.1 模型建立选用高斯图模型来模拟网络数据。设X为p维服从多元高斯分布的随机变量,即
| $ \boldsymbol{X}=\left(x_{1}, \cdots, x_{p}\right)^{\mathrm{T}} \sim N\left(\boldsymbol{\mu}, \mathit{\pmb{\Sigma}}^{*}\right). $ | (1) |
定义μ为p维均值向量,Σ*为协方差矩阵。设G=(V, E)为高斯无向图,V={x1, …, xp}为G的顶点集,E={(i, j)}为高斯图模型边的集合。xi与xj满足以下的性质
| $ x_{i} \perp x_{j} \mid x_{-(i, j)} \Leftrightarrow(i, j) \notin E, $ |
也就是xi和xj之间无边与xi和xj条件独立相互等价。
设Θ*=(Σ*)-1为G的精度矩阵。文献[7]提出,在G中,xi和xj的边由精度矩阵的元素Θij*来表示。当Θij*≠0时,xi和xj之间有边。当Θij*=0时,xi和xj之间无边。设υ={1, …, p},定义S={(i, j)∈υ×υ|Θij*≠0}为精度矩阵的支撑集。恢复G等价于恢复Θ*的支撑集。
设X1,…,Xn∈
本节将基于ISEE估计量(innovated scalable efficient estimation)构造De-ISEE统计量。ISEE方法是由Fan和Lyu[15]提出,是为了高效地估计超高维精度矩阵的点估计。他们是受创新变换的启示,将估计精度矩阵的问题转化为大协方差矩阵估计问题。它的求解如下:
通过创新变换得到Y=Θ*X,则有Y~N(0,Θ*)成立。则估计Θ*的问题可转变为估计Y的协方差。为了估计Y,Fan等将长向量Y分解成小的子向量,即:
| $ \boldsymbol{Y}_{A}=\mathit{\pmb{\Theta}}_{A, A}^{*} \boldsymbol{\eta}_{A}, $ |
这里
因为X~N(0, Σ*),则对于任意的A,有XA⊥XAC~N(-ΘA, A*-1ΘA, AC*XACΘA, A*-1)成立。由此得到以下的多元线性回归模型:
| $ \boldsymbol{X}_{A}=\boldsymbol{X}_{A^C} \boldsymbol{C}_{A}+\boldsymbol{\eta}_{A}, $ | (2) |
这里CA=-ΘAC, A*ΘA, A*-1是回归系数矩阵,ηA~N(0, ΘA, A*-1为模型的误差向量。
为估计残差向量ηA,用文献[25]提出的scaled Lasso惩罚回归的方法对模型(2)进行拟合。对于(2)中A的每个节点j,有
| $ \boldsymbol{X}_{j}=\boldsymbol{X}_{A^C} \boldsymbol{\beta}_{j}+\boldsymbol{\eta}_{j}, $ | (3) |
这里Xj, βj, ηj分别是XA, CA, ηA的第j个列向量。对(3)进行scaled Lasso惩罚回归:
| $ \begin{gathered} \left(\hat{\beta}_{j}, \hat{\sigma}\right)=\arg \min _{\beta \in \mathbb{R}^{p-|A|, }\sigma \geqslant 0} \\ \left\{\frac{\left\|X_{j}-X_{A^C} \beta\right\|_{2}^{2}}{2 n \sigma}+\frac{\sigma}{2}+\lambda \sum\nolimits_{k \in A^C} \frac{\left\|X_{k}\right\|_{2}}{\sqrt{n}}\left\|\beta_{k}\right\|_{1}\right\}, \end{gathered} $ |
这里‖υ‖q为任意给定向量υ的Lq范数,σ=var1/2(ηj)。可得
由此得到ΘA, A*的估计为
| $ \hat{\boldsymbol{Y}}=\left(\hat{\boldsymbol{Y}}_{A_{t}}\right)_{1 \leqslant l \leqslant L,} $ |
这里(Al)l=1L为索引集(1, …, p}的一个分割,即:Ul=1LAl={1, …, p},以及对于任意的1≤l≠m≤L, Al∩Am=Ø。
据此得到Y的样本协方差矩阵的初始ISEE估计量为
| $ \hat{\mathit{\pmb{\Theta}}}=T_{\tau}\left(\hat{\mathit{\pmb{\Theta}}}_{\mathrm{ISEE}, \text { ini }}\right), $ |
这里
由于ISEE估计量计算步骤的复杂性,以致很难研究ISEE估计量的分布性质。为了构建精度矩阵Θ*基于ISEE估计量的置信区间,本文需要一个优良的统计量。为要消除正则化惩罚为ISEE估计量带来的偏差,本文受文献[19, 22]构造去偏统计量的启发,基于文献[22]提出的渐近正态模型
| $ \left(2 \hat{\mathit{\pmb{\Theta}}}-\hat{\mathit{\pmb{\Theta}}} \hat{\mathit{\pmb{\Sigma}}} \hat{\mathit{\pmb{\Theta}}}-\mathit{\pmb{\Theta}}^{*}\right)_{i j} \stackrel{d}{\longrightarrow} N\left(0, \sigma_{i j}^{2} / n\right), $ |
构建De-ISEE统计量
| $ \hat{\boldsymbol{T}}=2 \hat{\mathit{\pmb{\Theta}}}-\hat{\mathit{\pmb{\Theta}}} \hat{\mathit{\pmb{\Sigma}}} \hat{\mathit{\pmb{\Theta}}}, $ | (4) |
其中
| $ \begin{gathered} I_{i j, \alpha} \equiv I_{i j}\left(\hat{\mathit{\Theta}}_{i j}, \alpha, n\right)=\left[\hat{T}_{i j}-\Phi^{-1}(1-\alpha / 2) \hat{\sigma}_{i j} / \sqrt{n}, \right. \\ \left.\hat{T}_{i j}+\Phi^{-1}(1-\alpha / 2) \hat{\sigma}_{i j} / \sqrt{n}\right], \end{gathered} $ | (5) |
此处
由式(4)可看出
通过仿真实验来检验De-ISEE统计量对网络数据变量联系的恢复效果及计算效率。并与De-Glasso统计量[22]进行对比研究。
采用文献[22]中的模拟设定,用多元高斯分布Np(0, Σ*)来模拟网络数据,其中p为维度。设置精度矩阵Θ*=tridiag(ρ, 1, ρ)为参数ρ>0的三对角矩阵。样本量都设为n=500,分别使用De-ISEE方法、De-Glasso方法来计算Θij*的置信区间。为比较方便,本节考虑置信水平为90 %,95 %,99 %的置信区间。
在仿真实验中,当计算De-Glasso时,使用R包(Glasso版本1.10)。它的调节参数使用五折交叉验证从10值的网格中选择。交叉验证的损失函数使用Cai等[17]提出的L(Σ,Θ)=
使用文献[22-24]使用的平均覆盖率指标来比较两种方法的覆盖准确性。分别为: ACS,ALS,ACSc,ALSc。其中ACS为在支撑集S上的平均覆盖率,它的定义为
| $ \mathrm{AC}_{S}=\frac{1}{|S|} \sum_{(i, j) \in S} \hat{\alpha}_{i j}, $ |
这里
| $ \mathrm{AL}_{S}=\frac{1}{|S|} \sum_{(i, j) \in S} \hat{C}_{i j}, $ |
这里
|
|
表 1 ρ=0.3时, De-ISEE方法与De-Glasso方法平均覆盖率的比较 Table 1 The comparision of average coverage for De-ISEE method and De-Glasso method when ρ=0.3 |
表 1分别展示维度p=200, 1 000, 2 000, ρ=0.3时,De-ISEE统计量与De-Glasso统计量构成的置信区间平均覆盖率的比较。当p=2 000时,由于De-Glasso统计量计算时间过长,为避免过多的计算损失,只计算De-ISEE统计量的平均覆盖率。
可以看出,当精度矩阵维度p<n时,De-ISEE统计量与De-Glasso统计量均能很好地恢复图模型。然而当维度p>n时,De-Glasso方法在S上的平均覆盖率明显变小,甚至随着p的增加无法计算。而De-ISEE方法当p变大时,它的平均覆盖率基本维持不变。
另一方面,De-ISEE方法在S上的平均覆盖率始终高于De-Glasso方法,而De-Glasso方法在SC上的平均覆盖率始终高于De-ISEE方法。这表明由De-Glasso方法恢复的图模型更容易丢失变量间联系。这不利于在海量信息中挖掘变量间联系。大数据时代促使网络数据的维度激增,例如在经济分析中,影响经济的因素越来越多,然而各个因素之间的联系却是广泛而又稀疏的。这就需要借助工具发现变量间联系,再针对性分析。De-ISEE统计量很好地恢复了图模型,由它得出的平均覆盖率更接近理想覆盖率。这也在一定程度上,弥补了De-ISEE方法平均置信区间长度长于De-Glasso方法平均置信区间长度这一缺陷。另外,平均置信区间长度也在某种程度上反映了样本的随机误差。
为验证De-ISEE统计量的稳定性,设置另一参数ρ= 0.4,计算结果见表 2。
|
|
表 2 ρ=0.4时, De-ISEE方法与De-Glasso方法平均覆盖率的比较 Table 2 The comparision of average coverage for De-ISEE method and De-Glasso method when ρ=0.4 |
表 2设置了一个更大的三对角矩阵参数值ρ。同理,为了节省时间与空间损失,在表 2中,当p=2 000时,只计算De-ISEE方法的平均覆盖率。可以发现表 2的结论与表 1保持一致。并且相比较于表 1,可发现当参数值ρ变大时,De-Glasso方法在S上的平均覆盖率明显变小,而De-ISEE统计量基本保持不变,可见De-ISEE方法不受参数值变化的影响,具有较高的稳定性。
为了比较计算效率,使用文献[15]使用的平均计算时间指标, 分别计算置信水平为1-α的De-ISEE方法和De-Glasso方法的CPU运行时间(s)对数的平均数。参数设置为n=500, ρ=0.3, α=0.05, N=100。计算结果为图 1,x轴为维度p,y轴为CPU运行时间(s)对数的平均数。
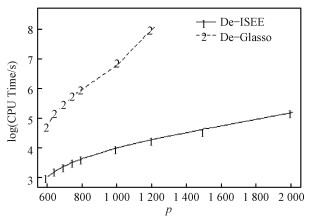
|
Download:
|
| 图 1 De-ISEE与De-Glasso随着维度p增加的CPU运行时间对数的平均数 Fig. 1 The average logarithm of CPU running times of De-ISEE and De-Glasso as dimensionality p increases | |
由图 1可见,随着维度p的增加,De-ISEE的平均运行时间增长缓慢,而De-Glasso的平均运行时间增长快速。当维度很高时,De-Glasso方法甚至无法计算。
综上可见,通过比较De-ISEE方法与De-Glasso方法的平均覆盖率,可发现,在高维网络数据中,De-ISEE方法的平均覆盖率不随维度p以及参数值ρ的变化而显著变化,具有较高的稳定性。而De-Glasso方法的平均覆盖率却对维度p和参数值ρ的变化较为敏感。当精度矩阵的维度p变大时,De-ISEE方法依旧计算高效。在处理高维矩阵时,无论从平均覆盖率,还是平均运算时间来看,De-ISEE方法都比De-Glasso方法有效。
3 实例分析将De-ISEE方法运用于实际网络数据,选用2个实际数据集,分别运用De-ISEE及De-Glasso方法来恢复网络数据间的联系。网络数据间的联系形成图模型,本节的目标是分别运用2种方法计算图模型精度矩阵的置信区间,比较它们恢复图模型的边以及各自运行时间。第1个数据集是由枯草芽孢杆菌产生的核黄素(维生素B2)数据集,可在hdi R包中获得。第2个数据集是前列腺肿瘤基因表达数据集(prostate tumor gene expression),它来自于spls R包。
对于这2个数据集,为了更方便地分析,选择前500个方差最大的变量进行建模。随后分离样本,用10个随机选择的观察值来估计500个变量的方差。再次利用估计的方差缩放剩余观察值的设计矩阵。在实例分析中,当计算De-ISEE统计量时,调优参数λ选用Fan和L[15]提出的λ=B/(n-1+B2)1/2,这里B定义为B=tq(1-n1/2/(2p log p), n-1),tq(a, m)为自由度为m、下分位数为α的t分布。在计算De-Glasso统计量时,与仿真实验同理,选用5折交叉验证选择调节参数。显著性水平都设为α=0.05。
第1个数据集包含n=71个枯草芽孢杆菌的转基因突变体,它有p=4 088个基因表达水平的对数观察变量。我们选择前500个方差最大的变量,也就是一个完整的图包含(2500)条边。计算结果显示,De-ISEE统计量得到28条边为显著的,它的CPU运行时间为1.643 s。De-Glasso统计量识别出5条边为显著的[22],它的CPU运行时间为3.756 s。对2种方法识别出的边集进行对比发现,由De-Glasso统计量识别的边是De-ISEE识别边的子集。
第2个数据集包含n=102个样本观察值以及p=6 033个变量。本节分别使用De-ISEE方法与De-Glasso方法计算置信区间以此来识别边。通过De-ISEE方法可识别出121条边为显著的,它的CPU运行时间为1.994 s。De-Glasso方法识别出28条边为显著的,它的CPU运行时间为4.013 s。通过对比再次发现,由De-Glasso统计量识别的边是De-ISEE识别边的子集。且De-ISEE方法的计算速度比De-Glasso方法快。
这样的结论与仿真实验类似,De-Glasso方法识别出的边集更稀疏,容易遗漏个体间的联系。而De-ISEE方法估计的边集基本涵盖真实边集。在个体数量逐渐增加的网络数据中,个体与个体之间的联系广泛而又稀疏,通过De-ISEE方法发现个体之间潜在的联系可以帮助研究者从庞大的数据信息中发现有用信息,进而有针对性地进行分析。在第2个数据集中,De-ISEE方法还可以作为分析人类基因的补充工具。
4 结论与展望本文提出De-ISEE统计量,并且对其进行了仿真实验以及实例分析。与其他方法相比,由于ISEE点估计具有可伸缩、易调优等优点,De-ISEE统计量得出的平均覆盖率更接近于真实覆盖率,且计算更为快速,可以处理超高维矩阵。这对挖掘高维网络数据间的联系具有很重要的作用。例如在实例分析中分析的核黄素数据集以及前列腺肿瘤基因表达数据集,De-ISEE统计量可以精确恢复变量间的联系,从广泛的信息网中帮助研究者提取重要信息,也可作为研究人类基因联系的补充工具。
本文给出了De-ISEE统计量的实用价值,还尚需要一定的理论支撑,这将会是接下来研究的问题。此外,对图模型构建同时置信区间也将是我们进一步研究的问题。
| [1] |
王新栋, 于华, 江成. 社交网络关键节点检测的积极效应问题[J]. 中国科学院大学学报, 2019, 36(3): 425-432. Doi:10.7523/j.issn.2095-6134.2019.03.017 |
| [2] |
Fan J, Liao Y, Liu H. An overview of the estimation of large covariance and precision matrices[J]. Economet J, 2016, 19(1): C1-C32. Doi:10.1111/ectj.12061 |
| [3] |
Chen X, Liu Y, Liu H, et al. Learning spatial-temporal varying graphs with applications to climate data analysis[C]//Twenty-Fourth AAAI Conference on Artificial Intelligence: AAAI Press, 2010: 425-430.
|
| [4] |
Schäfer J, Strimmer K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics[J]. Stat Appl Genet Mol Biol, 2005, 4(1): Article 32. Doi:10.2202/1544-6115.1175 |
| [5] |
Wainwright M J, Jordan M I. Graphical models, exponential families, and variational inference[J]. Found Trends Mach Learn, 2008, 1(1/2): 1-305. Doi:10.1561/2200000001 |
| [6] |
Liu H, Lafferty J D, Wasserman L A. The nonparanormal: semiparametric estimation of high dimensional undirected graphs[J]. J Mach Learn Res, 2009, 10(3): 2295-2328. |
| [7] |
Lauritzen S. Graphical models[M]. New York: Oxford Univ Press, 1996.
|
| [8] |
Meinshausen N, Bühlmann P. High-dimensional graphs and variable selection with the lasso[J]. Ann Statist, 2006, 34(3): 1436-1462. Doi:10.1214/009053606000000281 |
| [9] |
Yuan M, Lin Y. Model selection and estimation in the Gaussian graphical model[J]. Biometrika, 2007, 94(1): 19-35. Doi:10.1093/biomet/asm018 |
| [10] |
Bickel P, Levina E. Covariance regularization by thresholding[J]. Ann Statist, 2008, 36(6): 2577-2604. Doi:10.1214/08-aos600 |
| [11] |
Friedman J, Hastie T, Tibshirani R, et al. Sparse inverse covariance estimation with the graphical lasso[J]. Biostatistics, 2007, 9(3): 432-441. Doi:10.1093/biostatistics/kxm045 |
| [12] |
Zhang T, Zou H. Sparse precision matrix estimation via lasso penalized D-trace loss[J]. Biometrika, 2014, 101: 103-120. Doi:10.1093/biomet/ast059 |
| [13] |
Liu W D, Luo X. Fast and adaptive sparse precision matrix estimation in high dimensions[J]. J Multivariate Anal, 2015, 135: 153-162. Doi:10.1016/j.jmva.2014.11.005 |
| [14] |
Ren Z, Sun T N, Zhang C H, et al. Asymptotic normality and optimalities in estimation of large Gaussian graphical models[J]. Ann Statist, 2015, 43(3): 991-1026. Doi:10.1214/14-aos1286 |
| [15] |
Fan Y, Lyu J C. Innovated scalable efficient estimation in ultra-large Gaussian graphical models[J]. Ann Statist, 2016, 44(5): 2098-2126. Doi:10.1214/15-aos1416 |
| [16] |
杨军, 于丹. 修如旧模型中储存系统备件量的计算及其置信区间[J]. 中国科学院研究生院学报, 2004, 21(4): 441-446. Doi:10.7523/j.issn.2095-6134.2004.4.002 |
| [17] |
Cai T, Liu W D, Luo X. A constrained L1 minimization approach to sparse precision matrix estimation[J]. J Amer Statist Assoc, 2011, 106(494): 594-607. Doi:10.1198/jasa.2011.tm10155 |
| [18] |
Nickl R, van de Geer S. Confidence sets in sparse regression[J]. Ann Statist, 2012, 41: 2852-2876. Doi:10.1214/13-aos1170 |
| [19] |
van de Geer S, Bühlmann P, Ritov Y, et al. On asymptotically optimal confidence regions and tests for high dimensional models[J]. Ann Statist, 2014, 42(3): 1166-1202. Doi:10.1214/14-aos1221 |
| [20] |
Meinshausen N. Assumption-free confidence intervals for groups of variables in sparse high-dimensional regression[J]. arXiv: 1309.3489, 2013.
|
| [21] |
Zhang C H, Zhang S S. Confidence intervals for low dimensional parameters in high dimensional liner models[J]. J Roy Statist Soc Ser B, 2014, 76(1): 217-242. Doi:10.1111/rssb.12026 |
| [22] |
Janková J, van de Geer S. Confidence intervals for high-dimensional inverse covariance estimation[J]. Electron J Stat, 2015, 9(1): 1205-1229. Doi:10.1214/15-ejs1031 |
| [23] |
Huang X, Li M. Confidence intervals for sparse precision matrix estimation via Lasso penalized D-trace loss[J]. Commun Stat Theor M, 2017, 46(24): 12299-12316. Doi:10.1080/03610926.2017.1295074 |
| [24] |
Janková J, van de Geer S. Inference in high-dimensional graphical models[J]. arXiv: 1801.08512, 2018.
|
| [25] |
Sun T N, Zhang C. Scaled sparse linear regression[J]. Biometrika, 2012, 99(4): 879-898. Doi:10.1093/biomet/ass043 |
 2022, Vol. 39
2022, Vol. 39 


