三维重建是一种将真实物体场景刻画为符合计算机逻辑表达的数学模型的技术, 在计算机图形学、计算机视觉以及虚拟现实等领域有广泛的应用。岩体三维数值模型在岩石工程领域可以作为有限元、离散元、非连续变形分析等数值分析方法的模型输入, 其数值分析结果对岩体稳定性判断、关键块体识别以及在工程实施过程中做出科学决策起着重要作用。因此, 利用三维重建技术建立岩体三维数值模型在岩体工程领域有着十分重要的地位。
在三维模型重建中, 三维激光扫描技术因其采集数据速度快、精度高, 逐渐成为重建数据获取主流方式之一。三维扫描仪获取的点云数据是能够刻画物体表面特性的空间数据, 为描述三维现实世界提供了最直接和有效的表达方式。
然而, 在使用如图 1(a)所示的三维扫描仪扫描岩体点云数据的过程中, 由于扫描测量角度不同, 扫描仪对不同距离的岩体表面进行扫描所获得的数据信息的准确度和精度也是不同的。在目标岩体中, 由于如图 1(b)所示的障碍物的阴影和遮挡等问题都会导致采集的点云数据丢失一部分。岩体自身的复杂拓扑结构也会导致扫描数据的缺失; 此外, 原始点云的滤波处理和障碍物移除等前期工作, 也会导致点云数据中出现无法预料的数据丢失。数据丢失会导致岩体表面产生孔洞, 从而在一定程度上影响后续岩体模型重建结果的准确性。

|
Download:
|
| 图 1 扫描岩体数据示意图 Fig. 1 Scanning rock mass data | |
点云的孔洞检测及修复对后续的重建模型具有重要意义, 当前主流的点云孔洞检测与修复算法可分为基于三角网格和基于点云数据的算法。基于三角网格的修复算法比较成熟, 典型方法包括基于体素的修复和基于表面重建的修复; 而基于点云数据的修复算法则往往针对特定类型的模型进行修复, 如垂直建筑物和文物模型等。以上方法更适用于形状规则、密度均匀的三维点云模型。虽然主流算法能够满足多类模型的修复需求, 但是在实际工程计算中, 由于扫描的岩体点云数据量太大、噪声和离群点较多、孔洞数目多且复杂, 现有的检测和修复方法都不能对大型岩体点云数据获得满意的修复效果。
由于真实岩体点云中包含大量不规则平面, 平面提取是岩体点云数据处理的重要环节, 本文提出基于平面提取的岩体点云孔洞检测与修复方法。目前岩体平面提取算法主要包括基于区域生长[1]、基于模型拟合[2]及基于特征聚类[3]等3类方法。本文首先采用一种优化的区域生长算法进行平面提取, 然后在平面提取的结果上, 将点云映射至对应平面获取邻域夹角, 通过设置点云邻域夹角阈值检测孔洞边界。接着根据孔洞边界点集所属平面及拟合误差划分孔洞类型, 通过拟合平面并新增采样点修复孔洞。由于平面提取过程包含数据去噪、平面合并等过程, 可以过滤绝大部分的噪声点, 对后续岩体点云数据孔洞修复的计算有直接的简化作用。本文算法无需对点云进行网格化处理, 可以快速有效地解决岩体点云数据的修复问题。
1 相关工作针对研究目的和适用领域的不同, 研究者们提出了大量的孔洞检测与修复算法。本文仅介绍应用较广泛、较前沿的算法, 更多详细的检测与修复算法可参考文献[4-5]。
1.1 孔洞检测点云孔洞检测环节对后续孔洞修复流程来说十分重要。目前孔洞检测算法主要包括基于三角网格与基于点云数据的两类检测算法。基于三角网格的孔洞识别通过将三维点云模型三角网格化, 在三角网格结构中, 根据三角形面片的拓扑关系进行孔洞识别。当网格模型较大时, 孔洞边界点判断计算量会随之加大, 效率随之降低。
基于点云数据的孔洞检测方法一般是通过建立点云空间索引, 遍历点云数据, 根据孔洞边界点的不同特征设置阈值过滤条件, 从而提取孔洞边界点。根据空间维度不同, 基于点云数据的识别算法又可分为基于二维平面投影映射的识别和基于三维空间的识别。基于二维平面投影映射的边界识别典型算法包括创建投影平面, 计算投影点的角度标准阈值差, 从而确定孔洞边界点[6]; 对投影点进行参数化后, 根据邻域点集在采样点处的场力大小之和可以表示点集的平均值, 设置阈值, 从而识别点云的边界特征点[7]; 其他还包括加权度量[8]、吊锤法[4]等判别边界特征点。基于三维空间的边界识别算法则多考虑点云数据本身的三维特征, 基于点云曲率、邻域点法向夹角等设置单一或混合阈值进行检测, 该类算法对参数设置敏感度高。此外, 针对特定的点云数据, 还有基于核回归[9]等边界提取方法, 该类算法不通过阈值参数提取孔洞边界, 适用于特定的内部不规则尖锐孔洞的识别优化。
1.2 孔洞修复目前点云的孔洞修复算法也主要包括基于三角网格的孔洞修复和基于点云数据的孔洞修复。基于三角网格的孔洞修复主要分为基于体素的算法和基于表面的算法。基于体素的修复算法首先将网格模型变换成由体素表示的模型, 然后在离散空间中应用不同的方法进行孔洞修复, 其采用的典型算法为有向体素融合, 在此基础上根据孔洞邻域表面信息, 使用多种偏微分方程进行聚敛优化等[10-12]。基于表面的典型算法则是在描述点云的拓扑结构后, 根据特征线匹配、几何特征、形状计算和能量函数、径向基函数等[13-16]进行孔洞修复。总体来说, 基于三角网格的修复对于一般的规则物体(如机械零件、动物点云模型)具有较好的修复效果, 对不规则的大型点云模型或孔洞区域较大的网格模型修复效果不佳[17]。
直接对点云数据进行修复的研究包括将曲线拟合的方法应用到建筑物垂直面的点云孔洞修复中, 对点云数据投影至二维平面并进行拟合, 再恢复至三维空间插入数据点[18]; 针对由稀疏3D体积构成的高程面中的孔洞, 将点云数据投影到二维平面上, 按内外顺序依次计算孔洞内部填充点二维坐标, 再根据邻域点作用关系补齐三维坐标[19]; 其他算法还包括利用八叉树构建隐式曲面[20]等。基于点云数据进行修复的算法大都依赖孔洞周围区域信息, 对较大孔洞和边界开孔洞无法提取有效的周围区域信息, 存在提取点云边界不准确、错误识别孔洞、耗时长等问题, 修复效果不佳[5]。此外, 将神经网络应用于点云孔洞修复中也是近年来的算法尝试趋势, 包括在修复软件的基础上, 通过改进的BP神经网络重设置初始权值和阈值, 对修复数据进行优化等[21]。该类方法适用范围较小, 对特定模型调整神经网络算法模型参数耗时也较多。目前已有的修复方法大多适用于一般的规则点云模型, 本文根据岩体点云的平面特性, 在平面提取结果的基础上进行点云孔洞检测与修复。
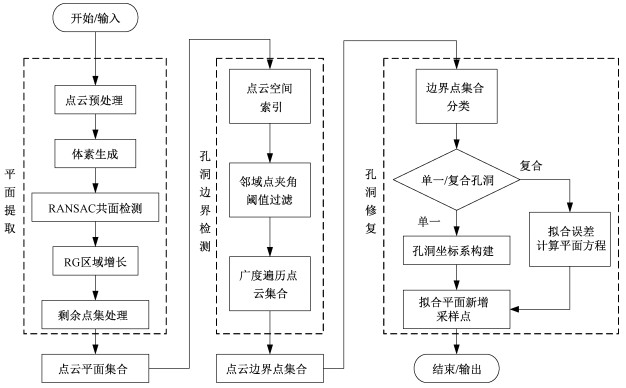
2 本文算法本文提出的基于岩体点云平面提取的孔洞检测与修复算法流程图如图 2所示。由于三维扫描激光扫描得到的高精度、大尺寸的岩体点云数据会消耗大量的存储空间, 从而影响修复的速度和效率, 为了得到良好的岩体点云修复效果, 需要解决以下问题: 如何有效地对输入的大规模且含较多噪声点的岩体点云进行孔洞检测; 如何快速准确地修复岩体点云中出现的大尺寸孔洞。由于岩体数据量大、密度不均匀且夹杂很多离群点, 应用一种优化的平面提取算法对离群点和噪声点进行过滤, 从而减少误差和冗余计算的时间。对岩体点云构建快速空间索引, 在拟合平面的基础上进行修复, 保留原始岩体点云的几何特征, 从而达到快速准确修复的目的。
|
Download:
|
| 图 2 孔洞检测与修复算法流程图 Fig. 2 Flow chart of holes detection and filling algorithm | |
因此, 本文算法主要包括3个步骤: 基于优化区域生长的平面提取、点云孔洞检测与孔洞分类修复。该算法通过平面提取对岩体点云数据进行去噪及分类处理, 提高了孔洞边界检测的效率; 平面提取的平面拟合结果也可直接用于后续的孔洞修复中的特征面建立, 使得孔洞检测与修复算法更为高效。
2.1 平面提取使用一种适用于岩体点云的优化区域生长算法[22]进行平面提取, 研究对象为岩体点云模型Rock1-3。区域生长是一种稳健高效的平面提取算法, 首先算法对激光扫描仪采集到的原始点云进行预处理, 去除无效点, 计算每个点的法向量。其次, 将剩余点云根据分辨率划分为体素, 使用RANSAC算法初步识别每个体素中的平面。然后将所有体素中的最大平面作为生长单元, 采用区域生长算法聚集相似平面的体素。最后, 将未分配的点集进行二次生长并映射至相邻平面, 提取出岩体点云所有的平面集合。
点云预处理 通常扫描的原始点云中包含噪声点, 这些噪声点会影响平面提取的准确性。因此首先对输入点云数据建立kd-tree空间索引, 然后遍历全部点云及其对应邻域数据, 删除孤立、异常坐标等噪声点。由于点的法向信息对后续不同方向的平面提取十分重要, 采用主成分分析法(principal components analysis, PCA) 估计法向信息。定义点云邻域为以点云中任意一点为中心的一定半径尺度的邻域球, 即该点与其邻域内的其他点组成的局部空间。对点云数据中的每一个点P(x, y, z), 在半径为r(考虑岩体点云平均密度分布, 此处设置r=0.5 m)的球面上查找其k(k=40)最近邻。构建点P的协方差矩阵, 然后选择与最小特征值相对应的特征向量, 作为点P的法向量。计算公式如下
| $ \sum=\frac{1}{k} \sum_{i=1}^k\left(\boldsymbol{P}_i-\bar{P}\right)\left(\boldsymbol{P}_i-\bar{P}\right)^{\mathrm{T}}, $ | (1) |
| $ \sum \cdot \boldsymbol{V}_j=\lambda_j \cdot \boldsymbol{V}_j, j \in\{0, 1, 2\}. $ | (2) |
其中: P为所有邻域点的均值点,Pi是点P的邻域点,λj是协方差矩阵Σ的特征值,Vj是特征值λj对应的特征向量。
生成体素 在三维空间中, 一个体素及其26个相邻体素构建为一个三阶立方体, 因此, 每个体素最多具有26个相邻体素。为了从点云中生成体素, 首先使用点云的三维坐标信息计算边界框。然后, 根据分辨率设置体素大小vsize将点云空间划分为体素, 同时建立相邻体素信息。最后, 删除空体素以提高体素查询效率。此步骤中, 体素大小的参数设置取决于岩体点云模型的尺寸规模和点云密度, 体素设置过大, 会导致每个体素内部包含多个平面, 影响后续合并过程; 体素设置过小, 可能会导致在拟合平面过程中容易受到噪声干扰, 且影响算法性能。通过实验调参, 此处对实验模型Rock1、Rock2设置参数为0.8 m, 对Rock3设置参数为0.65 m。
RANSAC平面检测 为了获得初始高质量的生长单元, 在每个体素中使用健壮的RANSAC算法检测平面, 选择体素中最大平面作为生长单元。为避免生成伪平面, 将法向量作为约束条件。平面检测算法每次从点云中选择3个非共线的点拟合平面, 然后统计点云中落在此平面上的散点个数, 将其作为该拟合平面的分数。若点到平面的距离小于给定阈值d且点法线与平面法线的夹角小于给定阈值angle, 则认为该点落在平面上, 经过T次迭代可以检测出最优平面。
假设点云数据共包含N个点, 其中最优平面包含n, 那么在一次检测中即可检测出最优平面的概率为p1, 则经过T次检测出最优平面的概率等于T次检测失败的补集, 假设经过T次, 至少检测出一次最优平面的最小概率为pt, 则可以计算出在此概率下的最小检测次数Tmin。
单次扫描中可检测到该平面的概率p1为
| $ p_1=\frac{\left(\begin{array}{l} n \\ 3 \end{array}\right)}{\left(\begin{array}{l} N \\ 3 \end{array}\right)} \approx\left(\frac{n}{N}\right)^3. $ | (3) |
T次试验后检测成功的概率pt为
| $ p_t=1-\left(1-p_1\right)^T=1-\left(1-\left(\frac{n}{N}\right)^3\right)^T. $ | (4) |
T次试验至少找到一组好的检测结果最小概率为
| $ T_{\min }=\frac{\log \left(1-p_t\right)}{\log \left(1-\left(\frac{n}{N}\right)^3\right)} \approx \frac{-\log \left(1-p_t\right)}{\left(\frac{n}{N}\right)^3}. $ | (5) |
RANSAC平面检测后, 每个体素只包含一个最优平面。由于后续步骤是以平面为生长单元的区域生长算法, 因此只有与当前平面相交的体素才是可生长体素。对每个体素内检测到的平面进行扩展, 并检测相邻体素与平面是否相交, 若不相交, 则该体素上的点集位于该平面的一端, 因此不属于同一平面, 将该相邻体素在邻域中删除。此步骤删除了一些无效邻近体素, 经过一次邻域优化, 重建了点云邻域信息, 可以减少后续进行区域生长步骤时的邻域搜索次数, 提升算法性能。
区域生长 本文使用区域生长算法从所有体素中检测平面。本文首先从体素集合选择包含最多点数的体素作为种子区域, 将两个体素的代表平面之间的距离(d=0.15 m)和两平面法线夹角(angle = 15°) 作为生长规则; 然后根据生长规则选择合适的相邻体素进行扩展, 直到所有相邻体素均已添加完毕, 得到一个平面点集, 重复这一步骤, 直至没有体素作为种子区域; 最后通过不断地添加新的种子区域, 迭代计算得到所有的平面点集合。
剩余点集处理 在区域生长完成后, 可以粗略检测出初始平面集U1。但是由于一个体素中可能包含多个平面, 因此在区域生长过程中, 一个体素中较小的平面点集可能未能分配至对应平面, 出现剩余点集。剩余点集主要存在于平面内部以及两个平面交界处, 内部点云被遗弃的主要原因是岩体表面粗糙度有变化, 导致这些点难以通过共面性检测; 边界处的剩余点云主要是因为法向量约束的限制以及边界处区域的复杂性, 这种现象导致了在共面性检测过程中小的平面被舍弃, 因而需要进行二次区域生长。
若剩余点集与其相邻平面满足二次区域生长的生长规则, 则将其添加到对应平面中进行二次区域生长, 生长规则与区域生长算法规则相同: 1)点P与平面的距离小于距离阈值; 2)点P的法向量与平面法向夹角小于角度阈值。此处剩余点集未被处理的主要原因是岩体点云粗糙性造成的平面点云信息丢失, 因此此处阈值参数比上文区域生长使用的阈值高出30% ~ 100% (d2=0.25 m, angle2=25°)。
表 1记录了本文平面提取算法的参数设置。最终, 算法将岩体点云中的所有点集都分配至对应平面, 得到最终的平面集合U2。
|
|
表 1 平面提取算法参数设置 Table 1 Parameter setting of plane extraction algorithm |
建立kd-tree点云空间索引后, 在岩体点云平面提取的基础上, 结合基于点云数据的边界提取算法, 通过分析岩体点云邻域点夹角来判断该点是否为边界点, 并据此提取孔洞边界。
对于结构特征复杂的岩体点云数据, 通过平面提取算法, 删去离群点等噪声点, 对保留的点云数据进行遍历, 依据kd-tree快速检索点的邻域信息。
此步骤中, 选取点云数据集中任意一点M, 当点M及邻域点集属于同一平面时, 将点M及其邻域点投影至对应平面, 根据下式计算其邻域夹角α。
| $ \partial=\sum\limits_{i=0}^{K-1} \theta\left(\overrightarrow{M_{i-1} M}, \overrightarrow{M M_i}\right) . $ | (6) |
其中: Mi为点M的有序相邻点集, K为邻域点个数, 0 < Mi < K。首先选取点M邻域中任意一点, 将该初始点记为M0, 迭代寻找下一个邻域点M1, 作向量
当点M及其邻域点集属于多个平面时, 将该点M及其对应邻域点分别映射至对应平面并求解相应的邻域夹角, 然后多个邻域夹角之和作为该点的对应邻域夹角。若点M的邻域夹角和小于阈值(结合岩体真实数据集特性, 本文设置为220°), 则加入孔洞边界点集, 否则作为平面内部点并舍弃。
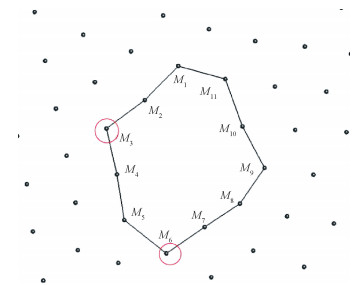
图 3展示了针对初始的点云边界提取结果, 由于阈值设置问题, 顶点M3与M6的邻域夹角大于设置阈值, 但其作为孔洞边界点并未被检测到。
|
Download:
|
| 图 3 未检测边界点示意图 Fig. 3 Not-detected boundary point diagram | |
对点云集合进行角度阈值过滤可以得到位于孔洞边界上的大部分顶点, 而初始的孔洞边界点集并不连通。因此对目前的孔洞边界点集进行广度优先遍历, 设置邻域半径(r=0.5 m)及相邻点数(k=30), 将不相邻的边界点集的最短路径上的顶点添加为孔洞边界点。然后迭代地在扩展后的孔洞边界点集中寻找最小点集合回路, 将得到的回路点集合作为孔洞点边界线。
2.3 孔洞修复本文算法在检测出的岩体点云孔洞边界线点集上进行孔洞修复。根据岩体点云平面提取结果, 将点云孔洞分类为单一平面孔洞和复合平面孔洞。定义所有边界点集位于同一平面内的孔洞为单一平面孔洞, 边界点集位于多个(大于等于2)平面相交处的孔洞为复合平面孔洞。
图 4(a)展示了所有边界点集位于同一平面内的孔洞; 图 4(b)展示了所有边界点集位于多个平面相交处的孔洞, 图 4红色圆框框出了孔洞局部放大区域。

|
Download:
|
| 图 4 平面不同孔洞图 Fig. 4 Different types of holes | |
孔洞修复步骤包括:
1) 构建孔洞坐标系, 计算孔洞邻近域的最小二乘拟合平面, 作为孔洞点及其邻近域的特征面。假设孔洞点及其邻近域的数据点可以用M0、M1、…、Mn-1来表示, 这些点到该特征面的距离的平方和应该最小。与前文平面提取算法中的计算方法类似, 计算该拟合平面的法线相当于求其协方差矩阵的最小特征值所对应的特征向量n, 根据空间平面方程原理即可求解。
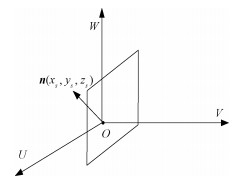
假设在孔洞坐标系中的3个坐标轴分别为U轴、V轴、W轴, 规定O作为该孔洞坐标系的原点, 特征面为UOV平面。将孔洞及其邻近域投影到该特征平面上, 特征面的法向量即为孔洞坐标系的W轴, 图 5给出了孔洞坐标系示例, 其中法向量为n(xs, ys, zs)。
|
Download:
|
| 图 5 孔洞坐标系示意图 Fig. 5 Hole coordinate system diagram | |
2) 新增采样点。对点云孔洞进行新增点采样, 将孔洞点及其邻近域投影至孔洞坐标系下, 进行二维投影, 在二维面内进行插值。为保证修复后的岩体点云具有密度一致性、后续重建保持完整的岩体几何拓扑连接, 此处选取原始岩体点云数据间的平均密度作为插值距离, 在二维投影面内进行等距差值。计算完毕后, 将孔洞坐标系变换为原始坐标系, 得到新增点采样结果。
经上述步骤后, 孔洞修复完成。针对前文不同分类孔洞, 将孔洞边界点集拟合平面, 当孔洞边界点集合与拟合平面的法向误差超过阈值(15°) 时, 判断该孔洞为复合孔洞, 否则为单一孔洞。对于单一孔洞, 根据上述步骤直接进行拟合修复。对于复合孔洞, 根据孔洞边界点集合选择其所属的多个邻域平面作为特征平面, 计算多个平面的交线, 然后在对应多个邻域平面内分别进行采样点集修复。最后迭代地修复提取到的所有孔洞, 完成孔洞修复。
3 实验与分析 3.1 实验说明为了验证本文算法的有效性, 本文展示了本文算法与基于点云数据的孟算法[18]和Hai算法[19]对多个岩体点云数据模型的修复效果图及量化对比, 以充分论证本文算法的良好性能。
本文算法以C++实现, 所采用的实验环境为IntelCorei5-6400CPU@2.70GHz, 8GB内存Windows1064位操作系统, 开源点云库PCL1.7.2 (Point Cloud Library, PCL)。实验数据为真实岩体点云模型Rock1-3, 点云数据中包含100000~ 600000个点。
3.2 实验结果与分析为验证算法的有效性, 分别在点云规模和孔洞复杂性不同的岩体点云上进行修复实验。
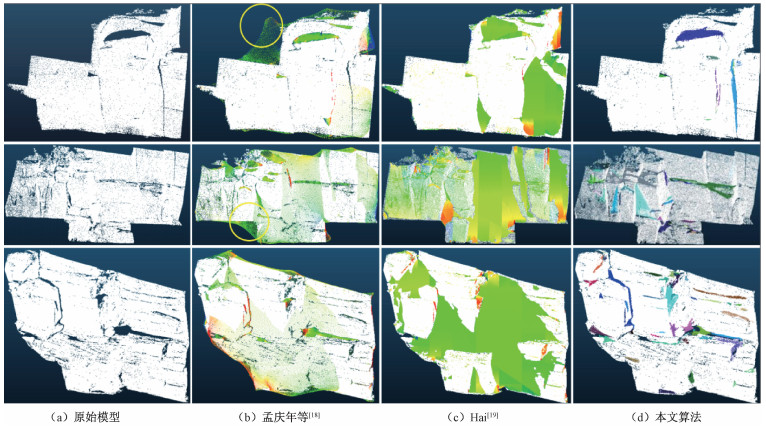
图 6分别展示了本文算法与其他算法对Rock1-3模型的修复对比。其中, 图 6(a)为各算法的原始输入模型Rock1-3的点云数据图, 6(b) 为孟庆年等[18]的修复算法效果, 6(c)为Hai[19]的修复算法效果, 6(d)为本文修复算法效果。图 6(b)、6(c)、6(d)中, 白色点云区域为原始点云数据, 彩色区域为各算法对应的实际修复点云, 所有实验结果在Cloud Compare中进行可视化显示。
|
Download:
|
| 图 6 Rock1-3修复效果对比图 Fig. 6 Rock1-3 filling effect comparison | |
如图 6所示, 在整体点云修复效果对比中, 本文算法修复效果最佳。在图 6(b)中, 孟算法[18]孔洞修复结果存在部分小孔洞未识别, 黄色圆框框出部分展示了在岩体点云密度不均匀处, 有多处错误修复, 在点云外部区域添加了多余的修复点集。图 6(c)中, Hai[19]也存在少量孔洞未识别的问题, 并且往往将几个孔洞合并为同一大孔洞修复, 破坏了原有的岩体点云结构, 导致修复结果错误。图 6(d)展示了本文算法的修复效果, 在岩体点云平面提取的结果上, 可以检测并修复绝大部分孔洞, 修复局部细节更为平滑, 与周围区域融合效果更佳, 并且保留了原有岩体点云特征和邻域信息, 边界特征清晰。
表 2展示了本文与其他算法的定量统计对比, Rock1-3原始模型原有孔洞初始值分别为11、26、37。对比项包括修复后的岩体点云数据顶点数Q(原始模型初始点云数记为Original), 算法对孔洞的检测数N、正确修复孔洞数M、修复错误数E, 其中E为未识别孔洞数与修复错误数的总和, 修复算法运行时间t/s。
|
|
表 2 Rock1-3模型修复定量对比 Table 2 Rock1-3 filling effect statistical comparison |
由表 2知, 从修复正确率上分析, Rock1模型中初始孔洞数11个, 本文算法全部正确识别并正确修复; Rock2模型中初始孔洞数26个, 本文算法正确识别25个并正确修复; Rock3模型中初始孔洞数37个, 本文算法正确识别35个并正确修复34个, 对比其他算法正确率更高。针对位于岩体外边界的孔洞, 本文算法存在部分未能正确修复的情况, 其原因为部分位于外边界上的孔洞无法有效检测。修复后的点云顶点数Hai[19]最多, 体现其修复质量不佳, 这是由于其算法更适用于垂直物高程面, 修复孔洞区域过大导致的; 孟庆年等[18]修复后的顶点数也比本文算法更多, 这是由于其部分孔洞未识别, 且修复点云错误导致的, 这在图 6中均有展示。
从算法运行效率上分析, 本文算法运行时间最短, 且随点云数据量的增加, 耗时增加较少, 这是由于算法考虑了岩体点云平面特性, 在平面提取的基础上不需要网格化和再次调参来提取点云特征, 因此在运行效率上有较大优势。孟庆年等[18]和Hai[19]由于需多次拟合误差, 在计算过程中耗时较长。由运行时间定量对比可知, 本文修复算法运行效率更高。
总体来说, 对于Rock1-3岩体点云模型, 本文算法对比其他基于点云数据的修复方法(孟庆年等[18]、Hai[19]), 能在最大程度上识别岩体点云原有的孔洞, 并对识别到的孔洞进行正确修复, 孔洞识别正确率最高, 同时修复错误率最小。
3.3 算法分析本文提出的算法针对岩体点云特性进行检测修复, 提高了岩体点云数据修复的准确性, 同时算法效率较高, 鲁棒性也较强。相较于其他基于点云数据修复的算法, 利用了岩体平面提取的特性, 平面提取时过滤了噪声点, 简化了后续边界提取步骤; 平面拟合过程简化了后续孔洞修复过程中的拟合孔洞平面步骤, 因此效率更高, 且针对大型不规则岩体点云数据修复适用性更好。其他算法则存在需要多次误差拟合导致计算变慢、对结构复杂的岩体点云模型不适用、对密度不均匀处的点云计算错误导致岩体孔洞误识别误修复等问题。
因此, 本文算法能较好较快地解决岩体点云数据孔洞检测与修复的问题, 对比已有修复方法, 修复准确性、运行效率更高, 对岩体点云模型适用性更佳, 优势明显。
4 总结提出一种基于岩体平面提取的点云数据检测修复方案, 算法的重要贡献之一在于首次将点云平面提取的结果应用于孔洞检测与修复, 理论上平面提取的效果越好, 算法最终的效果越好。从实验结果来看, 本方法针对于岩体点云模型, 孔洞修复识别率和正确率更高, 运行时间更快, 整体修复效果更佳。由于考虑岩体点云特性进行孔洞检测修复, 本文算法目前针对大型岩体点云模型效果良好, 对其他特性的点云数据集的适用性未做深入讨论, 这也是后续工作的一项重点, 另外, 由于在点云外边界处缺失数据未能有效地检测孔洞, 这部分工作也需要后续进一步研究。
| [1] |
Pu S, Vosselman G. Automatic extraction of building features from terrestrial laser scanning[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2006, 36(5): 25-27. |
| [2] |
Kotthäuser T, Mertsching B. Triangulation-based plane extraction for 3D point clouds[C]//Intelligent Robotics and Applications (ICIRA 2012). Springer, Berlin, Heidelberg, 2012: 217-228. DOI: 10.1007/978-3-642-33509-9_21.
|
| [3] |
Biosca J M, Lerma J L. Unsupervised robust planar segmentation of terrestrial laser scanner point clouds based on fuzzy clustering methods[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63(1): 84-98. Doi:10.1016/j.isprsjprs.2007.07.010 |
| [4] |
胡志胜. 三维激光扫描点云边界检测和孔洞修补技术研究[D]. 徐州: 中国矿业大学, 2016.
|
| [5] |
Guo X Y, Xiao J, Wang Y. A survey on algorithms of hole filling in 3D surface reconstruction[J]. The Visual Computer, 2018, 34(1): 93-103. Doi:10.1007/s00371-016-1316-y |
| [6] |
陈飞舟, 陈志杨, 丁展, 等. 基于径向基函数的残缺点云数据修复[J]. 计算机辅助设计与图形学学报, 2006, 18(9): 130-135. Doi:10.3321/j.issn:1003-9775.2006.09.023 |
| [7] |
陈义仁, 王一宾, 彭张节, 等. 一种改进的散乱点云边界特征点提取算法[J]. 计算机工程与应用, 2012, 48(23): 177-180, 190. Doi:10.3778/j.issn.1002-8331.2012.23.040 |
| [8] |
Bendels G H, Schnabel R, Klein R. Detecting holes in point set surfaces[J]. Journal of WSCG, 2006, 14(1-3): 89-96. |
| [9] |
Ztireli A C, Guennebaud G, Gross M. Feature preserving point set surfaces based on non-linear kernel regression[J]. Computer Graphics Forum, 2009, 28(2): 493-501. Doi:10.1111/j.1467-8659.2009.01388.x |
| [10] |
Ju T. Robust repair of polygonal models[J]. ACM Transactions on Graphics, 2004, 23(3): 888-895. Doi:10.1145/1015706.1015815 |
| [11] |
Kallis C, Deliparaschos K M, Moustris G P, et al. Incremental 2D Delaunay triangulation core implementation on FPGA for surface reconstruction via high-level synthesis[C]//2017 22nd IEEE International Conference on Emerging Technologies and Factory Automation (ETFA). September 12-15, 2017, Limassol, Cyprus. IEEE, 2017: 1-4. DOI: 10.1109/ETFA.2017.8247736.
|
| [12] |
Boltcheva D, Lévy B. Surface reconstruction by computing restricted Voronoi cells in parallel[J]. Computer-Aided Design, 2017, 90(1): 123-134. Doi:10.1016/j.cad.2017.05.011 |
| [13] |
Foks N L, Li Y G. Automatic boundary extraction from magnetic field data using triangular meshes[J]. GEOPHYSICS, 2016, 81(3). Doi:10.1190/geo2015-0112.1 |
| [14] |
刘震, 王艳宾, 白丽丽, 等. 曲面细节特征保持的三维模型孔洞修复方法[J]. 计算机辅助设计与图形学学报, 2016, 28(12): 2052-2059. |
| [15] |
Jun Y. A piecewise hole filling algorithm in reverse engineering[J]. Computer-Aided Design, 2005, 37(2): 263-270. Doi:10.1016/j.cad.2004.06.012 |
| [16] |
Altantsetseg E, Khorloo O, Matsuyama K, et al. Complex hole-filling algorithm for 3D models[C]//Proceedings of the Computer Graphics International Conference(CGI ′ 17). ACM, Yokohama, Japan. 2017: 1-6. DOI: 10.1145/3095140.3095150.
|
| [17] |
张琦, 蔺素珍, 白佳璐, 等. 基于改进曲线收缩流方法的点云张开孔洞的虚拟修补[J]. 激光与光电子学进展, 2018, 55(9): 119-125. Doi:10.3788/LOP55.091002 |
| [18] |
孟庆年, 郑德华, 夏佳毅. 一种基于曲线拟合方法在建筑物垂直面点云孔洞修复中的应用[J]. 勘察科学技术, 2015(1): 40-43. Doi:10.3969/j.issn.1001-3946.2015.01.009 |
| [19] |
Hai T T. Filling holes in an elevation surface structured by a sparse 3D volume[D]. Ho Chi Ming City, Vietnam: International University HCMC, 2015.
|
| [20] |
Xie H, McDonnell K T, Qin H. Surface reconstruction of noisy and defective data sets [C]//IEEE Visualization 2004. October 10-15, 2004, Austin, TX, USA. IEEE, 2004: 259-266. DOI: 10.1109/VISUAL.2004.101.
|
| [21] |
王春香, 梁亮, 王耀, 等. 基于优化BP神经网络的点云孔洞修补效果比较分析[J]. 机床与液压, 2019, 47(16): 30-33, 69. Doi:10.3969/j.issn.1001-3881.2019.16.007 |
| [22] |
Hu L, Xiao J, Wang Y. Efficient and automatic plane detection approach for 3-D rock mass point clouds[J]. Multimedia Tools and Applications, 2020, 79(1/2): 839-864. Doi:10.1007/s11042-019-08189-6 |
 2022, Vol. 39
2022, Vol. 39 


