近年来，物联网(internet of things，IoT)的广泛应用和快速发展促进了雾计算(fog computing)网络的技术研究^[1]。通常认为物联网中的用户设备资源(如计算能力、能量等)有限，难以完成对处理时延要求较高的任务，而雾计算赋能网络是克服这一难题的一种非常具有前景的方法。在启用雾计算能力的物联网网络中，任务节点(task node，TN)可以选择将到达的任务卸载到附近的计算节点(computing node，CN)进行协同计算。通过共享雾赋能网络中的计算资源，可以大大减少网络的任务处理整体的时延。

目前针对雾计算网络中任务卸载问题的研究已有很多方面的工作^[2-4]。假设任务卸载场景中的系统参数(如CPU频率和数据传输速率)全部已知的情况下，任务卸载问题可以通过转化为一个确定性的优化问题，并进行求解。考虑更加复杂的任务卸载场景，为了应对节点或用户端配有实时状态任务队列池的情况，任务卸载问题可以转化为随机优化问题，继而利用李雅普诺夫(Lyapunov)优化方法来解决^[5-7]。而当系统参数(如任务达到率或节点移动路径等)部分未知的时候，原始问题可以转化为多臂老虎机问题，在这种情况下，系统算法需在每一步迭代更新中，在尝试探索学习新的系统参数还是直接利用已知的经验得出的最优卸载策略这两种选择之间进行权衡^[8-9]。

以上提到的这些工作都基于一个前提，即协助任务处理的计算节点的位置是固定的。在实际应用中，只有当任务节点处于计算节点的通信覆盖范围内时，计算节点才能够向任务节点提供计算服务。而每一个计算节点当前时刻可用的计算资源的总量也限制了它所能够提供服务的任务节点的数量。因此，计算节点在目标区域内的位置布局直接影响该区域雾赋能网络的任务卸载性能，其中包括无线通信覆盖范围和总任务处理时延。而针对具有多个任务节点的某片区域中的计算节点布局问题的研究文献目前很少。相似的工作包括如何对通信基站进行布局^[10-12]，然而这些工作仅考虑了通信网络中的无线通信覆盖问题，并没有考虑任务卸载的场景。为了减少系统总的任务处理等待时延，Maiti等^[13]设计了一种改进的K均值聚类算法，得到计算节点的位置选择。但是在该工作设置的场景中，由于计算节点需要设立在已有的网关之上，即为一部分网关增加任务处理的功能，因此计算节点放置的候选位置受到限制。同时，文中选择任意2个网关之间的距离作为聚类度量，当不同的任务节点具有不同数量的计算任务需求时，该方法找到计算节点的位置布局并不是最优的^[13]。

在雾计算网络中任务卸载问题的研究中，先前很少有工作研究如何实现计算节点的最优布局，本文将详细探讨这个问题。本文贡献总结如下。首先，假设任务节点的位置和任务到达率是已知的，而计算节点是边缘计算节点^[14]，并且可以在目标区域中任意布局。基于该假设，将该问题建模为计算节点的p中心问题。接着，对传统K均值在该情境下的应用进行探究。由于K均值算法对初始值敏感，进一步提出一种基于凸包的启发式算法，找到可支持任务节点通信和计算要求的最少计算节点数量和相应布局位置。

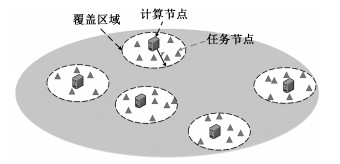
1 系统模型 1.1 网络模型

如图 1所示，考虑二维平面中的雾赋能网络，其中的雾节点按功能分为任务节点和计算节点两类。目标区域内任务节点的数量记作K。若干个计算节点将被布局到区域之中，其通常拥有较多计算资源，可以向所有任务节点提供无线通信和任务卸载服务，如实时环境数据上传和处理。计算节点数量记作N。令集合$\mathcal{K}=\{1, 2, \cdots, K\}$ 和集合$\mathcal{N}=\{1, 2, \cdots, N\}$分别表示任务节点的集合和计算节点的集合，第k个任务节点和第n个计算节点的二维平面坐标分别表示为ω_k=(x_k, y_k)和f_n=(x_n, y_n)。

为简化问题，假设所部署的计算节点具有相同的通信覆盖范围和计算能力。每个任务节点将会把任务卸载到正在与其通信的计算节点。假设每个产生的任务都是独立生成不可分的，计算节点之间不存在合作。每个计算节点的覆盖范围为半径为r的圆，处于覆盖半径内的任务节点可以与附近的计算节点进行通信，并向所连接的计算节点卸载任务。和文献[15-16]类似，我们将计算节点的任务处理过程建模为M/M/1队列，即该系统任务到达的时间遵循指数分布。具体地，在每个任务节点端，任务的产生为泊松流，每个任务的到达时间都是独立的，并且服从相同的指数分布。在每个计算节点端，任务处理过程为泊松流，其任务到达率为各任务节点的到达率之和。设第n个计算节点所连接服务的任务节点的到达率分别为$\lambda_{k}, k \in \mathcal{A}_{n}$，则计算节点n总的任务达到率为$\sum_{k \in \mathcal{A}_{n}} \lambda_{k}$，其中$\mathcal{A}_{n}$ 表示连接到第n个计算节点的任务节点组成的集合。

考虑到当需要大量的算力且通信量相对较小时，选择将任务进行卸载处理可以有效提升系统性能^[17]。因此，假设任务节点生成的任务需要很大的算力，必须卸载到计算节点进行计算，并且数据传输造成的延时与计算节点处的任务处理延时相比可以忽略不计。本文只关注任务在计算节点上的任务处理时延。

1.2 问题建模

在本文中，考虑尽可能降低计算节点布局成本，因此优化目标是令布局的计算节点数量N最小。为了确保任务处理的服务质量(quality of service，QoS)，每个计算节点的任务处理时延应小于τ_max。同时每个任务节点至少处于一个计算节点的无线覆盖范围内。因此，计算节点的最优布局可以建模为以下的优化问题：

$ \begin{array}{ll} \min \limits_{\left|f_{n}, \mathcal{A}_{n}\right|_{n \in N}} & |\mathcal{N}| \\ \text { s. t. } & \sum\limits_{n \in N}\left|\mathcal{A}_{n}\right| = K, \\ & \left\|\omega_{k}-f_{n}\right\|_{2} \leqslant r, \forall k \in \mathcal{A}_{n}, \forall n \in N, \\ & \frac{1}{\mu-\sum\limits_{k \in \mathcal{A}_{n}} \lambda_{k}} \leqslant \tau_{\max }, \forall n \in N, \end{array} $

(1)

式中：μ为计算节点的服务速率，表示单位时间内计算节点能够处理的平均任务数量；λ_k是第k个任务节点的到达率，表示单位时间内需要卸载处理的平均任务数量。约束1以及约束2确保已布局的计算节点覆盖所有任务节点。约束3表示的是任务处理延迟，它保证了任务卸载的QoS。

解决上述问题有2个困难。首先，这是一个p中心问题，而这是NP难的^[11]。同时传统的求解算法在此并不适用，这是因为某些计算节点可能会不满足平均任务处理时延的约束条件。另外，考虑到在实际应用场景中任务节点的数量较多，因此需要一个低复杂度的高效算法。

在介绍算法前，首先在命题1中给出在我们的问题当中需要布局的计算节点数量的一个下界。

命题1    设雾计算网络中任务节点的的任务到达率为{λ_k}_k=1^K，计算节点的任务处理过程建模为M/M/1排队系统，并且具有相同的服务速率μ且能够至少服务一个任务节点，即1/(μ-λ_max)≤τ_max。计算节点处理延迟不大于τ_max。因此，计算节点数量N受以下约束限制：

$ K \geqslant N \geqslant \frac{\tau_{\max }}{\tau_{\max } \mu-1} \sum\limits_{k = 1}^{K} \lambda_{k}. $

(2)

证明  对于第1个不等号，在最坏的情况下，每个计算节点只能服务到一个任务节点，因此有N≤K。

对于第2个不等号，我们考虑所有任务节点都集中分布在一个计算节点的通信覆盖范围内的情况。由于需要N个计算节点来满足任务卸载的QoS，由问题(1)中的第3个约束可得

$ \mu-\sum\limits_{k \in \mathcal{A}_{n}} \lambda_{k} \geqslant \frac{1}{\tau_{\max }}, \forall n \in N, $

(3)

将N个不等式加和，得

$ \mu N-\sum\limits_{k = 1}^{K} \lambda_{k} \geqslant \frac{N}{\tau_{\max }}, $

(4)

又因1/(μ-λ_max)≤τ_max，进一步有

$ N \geqslant \frac{\tau_{\max }}{\tau_{\max } \mu-1} \sum\limits_{k = 1}^{K} \lambda_{k}, $

(5)

证毕。

接下来，首先对传统K均值如何应用在该场景作了探究，给出改进的二分K均值聚类算法。进一步地，将致力于找到一种高效的螺旋计算节点布局算法来解决问题(1)。

2 计算节点布局算法 2.1 二分K均值聚类算法

作为对K均值聚类算法的一种改进版本，二分K均值聚类可看作是一种层次聚类方法^[18]。二分K均值聚类首先将所有未被聚类的点视为一个大类，然后使用传统K均值将不满足度量值要求的类进一步分为2个较小的类，重复上述步骤直到计算节点的数量等于给定数量N。

具体到我们的问题中，首先使用传统K均值反复进行二分操作，采用“是否满足约束条件”作为对当前类的度量，即当满足约束条件时，当前类不需要进一步划分，反之则需要继续使用传统K均值进行二分类。由于传统K均值计算得到的聚类中心并不一定满足要求，同时也为了确保传统K均值聚类中的任务节点能够尽可能多地被部署的计算节点覆盖，需要对聚类中心进一步调整，即求解聚类n形成的最小覆盖圆问题^[19]，并更新计算节点n的部署位置。最小覆盖圆问题可以转化为以下形式：

$ \begin{array}{ll} \min \limits_{\boldsymbol{f}_{n}} & r_{n} \\ \text { s. t. } & \left\|\omega_{k}-f_{n}\right\|_{2} \leqslant r_{n}, \quad \forall k \in \mathcal{A}_{n}, \end{array} $

(6)

式中：r_n表示覆盖集合$\mathcal{A}_{n}$中所有任务节点的最小圆的半径。应用文献[19]中的算法来解决问题(6)，此处不再展开。

定义一个变量s_n作为指示变量，来确定当前划分得到的聚类n是否满足约束条件，为

$ s_{n} = \left\{\begin{array}{c} 0, & r_{n} \leqslant r, \frac{1}{\mu-\sum\nolimits_{k \in \mathcal{A}_{n}} \lambda_{k}} \leqslant \tau_{\max }, \\ 1, & \text { 其他. } \end{array}\right. $

(7)

如果s_n=0，聚类n满足约束。若s_n=1，即当得到的聚类n不满足约束条件时，表示需要继续对其进行二分操作。将会被进一步划分的所选簇由

$ \mathcal{C} = \left\{n \mid s_{n} = 1\right\} $

(8)

给出。

与传统K均值算法相比，二分K均值聚类算法针对该场景进行了优化，无需预设最小数量的聚类即可确保其收敛性。二分K均值聚类算法具体流程见算法1。

算法1   MBKC(modified bisecting K-means clustering)布局算法

步骤1    初始化，设$n=1, \mathcal{A}_{1}=\mathcal{K}$。

步骤2    求解问题(6)，并计算第1个计算节点的位置和最小覆盖圆半径；

步骤3    计算指标s₁，更新$\mathcal{C}$；

步骤4   $ n=n+1, i=\min _{m \in \mathcal{C}} m$；

步骤5    簇$\mathcal{A}_{i}$ 通过二分K均值法分为2个新的簇$\mathcal{A}_{i}$和$\mathcal{A}_{n}$；

步骤6    根据式(6)和式(7)更新参数f_i, f_n和s_i, s_n；

步骤7  若$\sum_{j=1}^{n} s_{n}>0$，重复步骤4；

由于二分K均值算法中的传统K均值聚类对初始值敏感，为克服这个缺点，在下一节提供一种螺旋式布局的方法。

2.2 螺旋计算节点布局算法

受文献[11]的启发，我们以螺旋部署方式解决计算节点的布局问题。该算法遵循2个原则：第一，保证优先覆盖目标区域边界的任务节点；第二，以螺旋推进的方式沿着边界进行部署。

具体来说，给定K个任务节点的位置，先将未覆盖的任务节点集$\mathcal{K}_{U}$划分为边界任务节点子集$\mathcal{K}_{B}$和内部任务节点子集$\mathcal{K}_{I}$，即有$\mathcal{K}_{U}$ = $\mathcal{K}_{B}$∪$\mathcal{K}_{I}$。$\mathcal{K}_{B}$定义为目标区域中所有未覆盖的任务节点所组成的凸包的端点^[11]。

接着需要确定第一个计算节点的布局位置。首先，从$\mathcal{K}_{B}$中随机选择某个任务节点，记作标记节点k₀。该计算节点应布局在位置f₁处，保证覆盖到标记节点k₀和$\mathcal{K}_{U}$ 中的其他任务节点，并尽可能令覆盖到的任务节点数最大。具体地，可以通过解决以下问题来获得第n个计算节点的布局位置f_n以及连接到第n个计算节点的任务节点集合$\mathcal{A}_{n}$：

$ \begin{array}{ll} \max \limits_{f_{n}, \mathcal{A}_{n}}&\left|\mathcal{A}_{n}\right| \\ \text { s.t. } & k_{0} \in \mathcal{A}_{n}, \\ & \left\|\omega_{k}-f_{n}\right\|_{2} \leqslant r, \forall k \in \mathcal{A}_{n}, \\ & \frac{1}{\mu-\sum\nolimits_{k \in \mathcal{A}_{n}} \lambda_{k}} \leqslant \tau_{\max } \cdot \end{array} $

(9)

问题(9)是一个NP难的组合优化问题，我们使用文献[19]中最小覆盖圆算法求解。通过在每个步骤添加一个未覆盖的任务节点迭代更新集合$\mathcal{A}_{n}$和计算节点的位置f_n。如果计算节点的新位置满足问题(9)中的约束，则可以将该任务节点加入集合。

在布局第n个计算节点后，可以通过删去第n个计算节点所连接的任务节点来更新待覆盖任务节点集合_C，并通过找到集合_C的凸包来更新集合$\mathcal{K}_{B}$和$\mathcal{K}_{I}$。然后，在$\mathcal{K}_{B}$中选择新的标记节点。与文献[11]类似，沿着逆时针方向，把距离旧的标记节点最近的边界节点记作下一个标记节点。详细算法流程在算法2中列出。

算法2   SCNP(spiral computing node placement) 算法

步骤1   初始化，设$\mathcal{K}_{U}=\mathcal{K}, \mathcal{N}=\varnothing, n=1$, $\mathcal{A}_{n}=\varnothing$；

步骤2    将$\mathcal{K}_{U}$根据凸包定义划分为$\mathcal{K}_{B}$和$\mathcal{K}_{I}$；

步骤3    随机选取k₀∈ $\mathcal{K}_{B}$；

步骤4    令$f_{\text {temp }}=\omega_{k_{0}}, \mathcal{A}_{n}=k_{0}$；

步骤5    $ \mathcal{K}_{C}=\left\{k \mid\left\|\omega_{k}-\omega_{k_{0}}\right\|_{2} \leqslant 2 r, \forall k \in \right.$∈$\mathcal{K}_{U}$}，划定待覆盖任务节点集合；

步骤6    取距离最小点$k_{a}=\operatorname{argmin}_{k^{\prime} \in \mathcal{K}_{C}} \| \omega_{k^{\prime}}-$ $f_{\text {temp }} \|_{2};$

步骤7    计算{$\mathcal{A}_{n}$, k_a} 的最小覆盖圆，并判断是否满足通信覆盖和任务处理时延约束，若满足，则$\mathcal{A}_{n}$=$\mathcal{A}_{n}$∪k_a；

步骤8    若$\mathcal{K}_{C} \neq \varnothing$, 返回步骤4；

步骤9   更新$\mathcal{K}_{U}$, $\mathcal{K}_{B}$, $\mathcal{K}_{I}$, N；

步骤10    沿逆时针方向更新k₀，n=n+1；

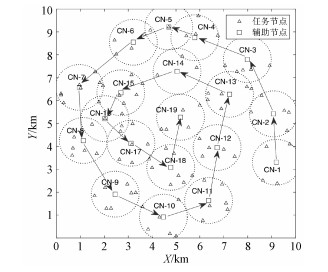
如图 2所示，算法从计算节点CN-1到CN-19由外向内依次逆时针连续螺旋部署，计算节点布局的轨迹构成一个螺旋曲线。

2.3 复杂度分析

接下来，给出两种算法对应的时间复杂度。

MBKC算法   对于二维欧几里德空间中的K均值聚类算法^[20]，其时间复杂度为O(KNI)，其中K, N, I分别表示任务节点数量、计算节点数量和算法收敛迭代次数。解最小覆盖圆问题时间复杂度为O(K′)^[19]，其中K′是被覆盖的任务节点数量，且有K′≤K。因此算法总时间复杂度为O(K²NI)，上界为O(K³I)。

SCNP算法    计算当前未被覆盖的任务节点的凸集其复杂度为O(Klog(K_b))，K_b表示当前处于边界上的任务节点的数量。解最小覆盖圆问题的复杂度上界为O(K)。另外，处理问题(9)中的约束2和约束3带来的复杂性是$2\left|\mathcal{K}_{C}\right|$，部署的计算节点的最大数量为任务节点数量K。总体复杂度有上界$O\left(K^{2} \log K+K^{3}+2 K\left|\mathcal{K}_{C}\right|\right)$。

3 仿真实验分析

本节将提供数值仿真实验结果测试本文所提出的计算节点布局算法的性能。

假设需要进行布局的物联网区域为半径5 km的圆形，在没有特殊指出的情况下，根据文献[15]，仿真参数设定为，任务节点在目标区域内随机均匀分布，其任务到达率λ_k是均值为100 s^-1的随机数，计算节点的服务速率μ为1 000 s^-1，计算节点服务的最大任务处理时延τ_max为0.02 s。根据文献[11]，设计算节点的通信覆盖半径r与目标区域比值为1 ∶5，即1 km。

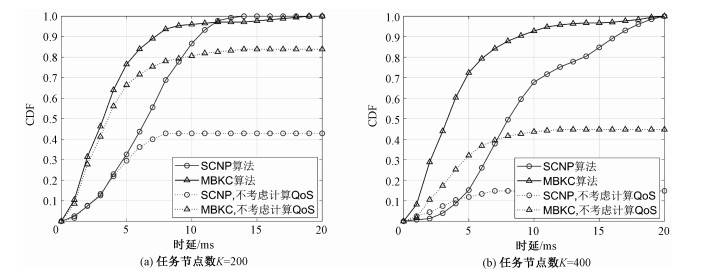
为测试本文提出的SCNP算法和MBKC算法的性能，图 3比较了不同算法下平均任务处理等待时间的累积分布函数(cumulative distribution function，CDF)，该曲线通过计算小于多个不同时延值的计算节点数量与布局的总数量的比值而得到。同时，在雾计算网络中对计算节点进行布局时，将任务处理时延纳入限制条件中的必要性得到了证明。在图 3(a)中，以任务节点数量200为例。当考虑计算QoS时，SCNP算法得到的计算节点数量为N_SCNP=27，MBKC算法为N_MBKC=35。当不考虑计算QoS时，分别为N′ _SCNP=21和N′ _MBKC=31。虽然部署的计算节点数量减少，但从CDF曲线可以看出，分别只有42.9 % 和83.9 % 的计算节点时延满足QoS要求，即τ≤τ_max。这说明在考虑服务QoS时，算法需要通过增加少量的计算节点，来保证所有计算节点的任务处理时延小于τ_max。同时还可以注意到，在图 3(b)中，以任务节点数400为例，MBKC算法中有93.4 % 的计算节点时延小于0.01 s，数量为56。而在SCNP算法中这个数字为71.8 %，数量为33。这说明与SCNP算法相比，MBKC算法的平均卸载任务处理等待时间更短，但代价是需要布局更多的计算节点。

为进一步测试算法的性能并分析任务节点数目对算法的影响，仿真比较了SCNP算法和MBKC算法在不同数量的任务节点场景下得到的最优计算节点数量，如图 4所示。“下界”是在命题1中得出的最小数量，根据$\tau_{\max } \sum_{k=1}^{K} \lambda_{k} /\left(\tau_{\max } \mu-1\right)$计算得到。从图中可以看出，随着任务节点数量的增加，SCNP算法始终优于MBKC算法，并且与下界保持更小的差值。这表明我们提出的SCNP算法在雾计算网络中，尤其是任务节点数量较大的场景下性能更优。这是由于SCNP算法在螺旋布局的过程中，优先保证边界上的任务节点沿着同一个方向被依次覆盖，并在迭代过程中不断缩小和更新边界，使得布局的计算节点的服务范围互相重叠的概率降低，充分利用了计算节点的服务能力。

在Maiti等^[13]的工作中，雾计算节点需要部署在已有的任务节点上。在这种情况下，计算节点的部署是“受限”的。图 4的仿真结果表明，无论是MBKC算法还是SCNP算法，“任意布局”的性能都要好于“受限布局”。当在区域内自由部署时，算法能对计算节点的位置进一步优化，而不受限于固定的位置。值得注意的是，虽然在部署受限且任务节点数量较少(K≤150)的情况下，基于K均值的MBKC算法能够得到更少的计算节点部署方案，但总的来说，SCNP算法更能胜任未来大规模雾计算网络的实际应用。这进一步凸显了我们工作的优势。

最后，通过比较算法的执行时间验证算法的复杂度，针对这点的验证是必要的，并且能够将运行时间和由仿真参数得到的理论分析进行比较。算法运行系统为Windows10，仿真软件为MATLAB 2019b，该计算机配有Intel i5-4430 3.0 GHz CPU和10 GB RAM，区域中任务节点的数量为400。MBKC算法和SCNP算法的复杂度比值为$I K^{2} /\left(K \log K+K^{2}+2\left|\mathcal{K}_{C}\right|\right)$，在实际仿真中I=10, K=100, $\left|\mathcal{K}_{C}\right|$=50，运行1 000次取均值。其中，SCNP算法执行时间t=0.023 0 s，MBKC算法执行时间t=0.229 s，比值为9.96，仿真结果说明其与理论分析得到的结果9.7基本一致。

4 结论

本文研究雾计算网络中计算节点的最优布局问题。考虑到任务处理的时延影响部署节点的服务QoS，希望找到可以同时满足任务节点通信覆盖和计算要求的最小数量的计算节点及其对应的布局位置。该问题是NP难的，目前没有理论上的最优解。为解决这个问题，给出该场景问题下所需计算节点数量的下界，并且提出低复杂度的启发式算法实现计算节点的布局。首先，基于二分K均值思路提出MBKC算法。接着，考虑到MBKC算法较为依赖于初始值的选取这一事实，基于螺旋布局策略进一步设计高效低复杂度的SCNP算法。此外，也提供了两种思路的布局算法的复杂度分析。数值结果证明了SCNP算法的优越性，并且该算法能够在任务节点较多的环境中以低复杂度得到趋向于下界的解。