2. 中国科学院大学数学科学学院, 北京 100049
2. School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
1995年Refregier和Javidi[1]提出利用4F系统的双随机加密算法(double random phase encoding, DRPE),一个明文图像经过2次傅里叶变换,通过频谱面和输出面的2块随机相位版作为“密钥”可以实现非常好的置乱效果。此后双随机加密算法被推广到其他光学系统中,如2004年Situ和Zhang[2]提出的菲涅尔域的双随机相位加密系统等。除上述4F系统和菲涅尔域的DRPE之外,还有各种变换下的DRPE系统[3-5]。为验证各种DRPE算法的安全性,对于上述加密系统的攻击也相继出现。Carnicer等[6]于2005年首次提出对于4F系统的双随机加密系统可以利用选择明文进行攻击,通过大量的设计好的选择明文,可以解出系统中所使用的密钥的相位分布,从而攻破系统。本课题组也曾提出对于菲涅尔域双随机加密的叠层攻击方法[7],取得了很好的效果。虽然上述攻击方法可以有效地破解加密系统,但是它们都具有一定的缺陷:首先,这些传统的攻击方法要求攻击者已知加密系统的一些先验信息(Kerckhoffs假设),比如加密系统的类型、系统所使用的波长,以及各步的衍射距离等结构参数等“非密钥”信息。其次,这些攻击多数依赖相位恢复迭代算法,由于迭代算法收敛性的限制,对于高像素图片的加密,或者加密系统过于复杂(多相位板等),迭代算法的攻击效果将显著下降。
为消除上述问题,需要对DRPE系统的性质进行更深入的研究。首先,以DRPE为例子,它是一个线性系统,光在每一个面的波前复振幅分布满足叠加原理,即不同位置处的点光源脉冲δ函数的彼此叠加满足格林函数积分关系,从而形成传播光场中的任意位置的波前函数。其次,它是一个纯相位的光学保守级联系统,早在1975年,霍裕平等[8]就指出:对于一般的纯相位非耗散保守光学系统,其对应的线性变换为幺正变换,经过验证,不论是4F系统的DRPE还是菲涅尔域的DRPE,均满足光学幺正变换的条件,也就是说当一组幺正的复振幅波前作为系统的输入时,系统的输出依然是一组幺正基。虽然看上去,这些“幺正基”都是一个个置乱很好的白噪声,但是其中隐含的幺正关系表明:DRPE系统其实置乱效果并不理想。这便是近20年来光学信息安全领域普遍忽略的性质。由于DRPE不仅是一个线性变换,同时还是一个幺正变换,那么对于其攻击可以自然而然地利用线性变换的矩阵理论进行攻击。幺正性进一步诠释了:在幺正光学加密系统中,明文和密文构成的2个线性空间彼此是幺正同构的,且其对应的子空间也是幺正同构的。利用这种同构性,可以忽略加密系统具体的结构属性,在利用数量远小于加密矩阵的秩的一系列选择明密文对直接重构加密过程的近似逆映射,从而实现对任意密文的直接破解。值得注意的是,这种方法是非迭代的,而且其攻击所需要的先验条件仅仅是幺正性,同时其所需要的算力和攻击结果与系统复杂度无关。也就是说,对于任意复杂的幺正系统,都可以通过一个固定的运算成本获得相同的攻击效果,且这个成本往往非常小,这是与传统攻击思路截然不同的。为表述的严谨,引入量子力学狄拉克符号来阐释其中的数学关系,进而提出基于线性幺正变换光学加密系统基于子空间投影法的一般性选择明文攻击原理,给出对应的数值模拟结果,以三相位板的菲涅尔域加密系统来展示对于一般线性幺正系统的攻击结果,证明这种攻击的有效性。而且,在充分利用系统幺正性的情况下,攻击者可以根据所需要的攻击效果任意选择选择明密文对的数量,以及可以实现包括局域攻击、彩色攻击等。
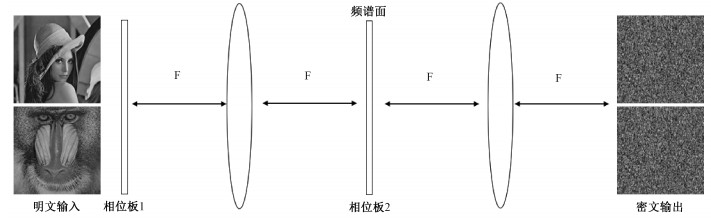
1 一般线性幺正光学系统20世纪70至80年代,霍裕平等对于利用纯相位的系统实现幺正变换以及线性变换做了大量的讨论[9-12]。其工作指出,对于一个非耗散的光学纯相位级联系统,其对应的线性变换是一种幺正变换,并且给出了用光学实现任意幺正变换以及线性变换的可能方法。20年后,Refregier和Javidi[1]提出4F系统中的DRPE加密算法,如图 1所示,如果把透镜看成是一个相位板,可以看出这是一个明显的纯相位线性幺正系统。
|
Download:
|
| 图 1 4F系统中的双随机加密 Fig. 1 DRPE encoding algorithm in 4F system | |
同理,菲涅尔域的DRPE以及其他纯相位的光学加密系统也是线性幺正系统。如果系统具有幺正性,那么意味着当选择一系列彼此正交的明文作为输入,那么输出的密文也是正交的。这就给了明文与密文很强的联系。一个很重要的数学性质便是:当选择明文空间V中的任一个明文|α〉,向V的某个子空间V‖做投影,那么投影系数与选择密文空间W=U(V)中的对应的密文|β〉向其对应子空间W‖中的投影系数相同,其中U对应置乱操作的酉变换。因此可以利用子空间投影的方法给出对于一般线性幺正光学加密系统的攻击方法。
2 对一般线性幺正光学加密系统的攻击原理 2.1 光学攻击的狄拉克符号理论考虑一个实际情形:某个黑客试图攻击一个加密系统,他需要破解加密系统从而实现对某一个特定密文的破解。传统攻击思路认为黑客可以知道加密系统所使用的算法以及系统中的结构参数,比如某个光学加密系统是菲涅尔域的DRPE系统,且各个相位板的位置以及加密所使用的波长对黑客是公开的,系统的安全性完全蕴含于密钥之中。所以只要破解了密钥的相位分布,那么系统就算被攻破了。而这种方法极度依赖于相位恢复算法所能给出的精度。或者,黑客可以不需要破解密钥的相位分布,仅需要知道系统是一个线性幺正系统。那么他可以把这个系统视为一个“黑盒子”,如图 2所示,只需要获得这个“黑盒子”对应的置乱映射,那么系统就算破解了。可以定义,系统的置乱算符为
| $ \left|\psi_{i}\right\rangle = \hat{G}\left|\phi_{i}\right\rangle . $ | (1) |

|
Download:
|
| 图 2 光学加密黑盒子 Fig. 2 Demonstration of encryption 'Blackbox' | |
定义:由|ϕi〉构成的空间称为明文空间,|ψi〉构成的空间为密文空间。其中i=1,2,…,N,N为明文和密文空间的维数,显而易见,N最大不超过加密系统所使用的像素数。而加密系统所使用的像素数是由采样定理和加密系统决定的,很明显这个数值一定很大,往往为几万至几百万像素的量级。也就是说对于攻击者而言,考虑理想情况,当其获得了N个明密文对|ϕi〉、|ψi〉时,即其拥有了明文和密文空间对应的一组完备基,那么必然存在系数CN=(c1,c2,…,cN),使得
| $ \left\{\begin{array}{l} |\alpha\rangle = c_{1}\left|\phi_{1}\right\rangle+c_{2}\left|\phi_{1}\right\rangle+\cdots C_{N}\left|\phi_{N}\right\rangle, \\ |\beta\rangle = c_{1}\left|\psi_{1}\right\rangle+c_{2}\left|\psi_{2}\right\rangle+\cdots C_{N}\left|\psi_{N}\right\rangle. \end{array}\right. $ | (2) |
其中:|α〉为待破解明文,|β〉为对应的已知密文,有
| $ \left\langle\phi_{i} \mid \phi_{j}\right\rangle = \delta_{i j} \text {, } $ | (3) |
〈ψi〉也必为密文空间的一组幺正基
| $ \left\langle\psi_{i} \mid \psi_{j}\right\rangle = \delta_{i j}, $ | (4) |
根据幺正条件,有
| $ c_{i} = \left\langle\psi_{j} \mid \beta\right\rangle . $ | (5) |
根据|ϕi〉和|ψi〉可以重新定义加密算符
| $ \hat{G} = \left|\psi_{i}\right\rangle\left\langle\phi_{i}\right| \text {. } $ | (6) |
同理,可以给出
| $ \hat{G}{}^{-1} = \left|\phi_{i}\right\rangle\left\langle\psi_{i}\right|, $ | (7) |
显然
| $ \hat{G}{}^{-1} \hat{G} = \hat{G} \hat{G}^{-1} = I . $ | (8) |
对于攻击者而言,往往并不能获得几万甚至是几百万的选择明密文对,即无法获得完备的|ψi〉,但是其总可以寻找一个|ψi〉的子空间,使得子空间的维数在可操作的范围,进而通过子空间投影的方法,获得明文的近似解。
分别定义在明文-密文空间的子空间投影算符
| $ \left\{\begin{array}{l} \hat{P}_{\phi} = \sum\nolimits_{i = 1}^{n}\left|\phi_{i}\right\rangle\left\langle\phi_{i}\right|, \\ \hat{P}_{\psi} = \sum\nolimits_{i = 1}^{n}\left|\psi_{i}\right\rangle\left\langle\psi_{i}\right|. \end{array}\right. $ | (9) |
则有
| $ \left\{\begin{array}{l} \left|\alpha_{\|}\right\rangle = \hat{P}_{\phi}|\alpha\rangle, \\ \left|\beta_{\|}\right\rangle = \hat{P}_{\psi}|\beta\rangle. \end{array}\right. $ | (10) |
其中:|α‖〉为待破解明文|α〉在|ϕi〉的n维子空间的投影, |β‖〉为|β〉在|ψi〉的n维子空间的投影。可以看出|α‖〉代表攻击结果与真实的明文|α〉的差异,当子空间维数n逐渐增大,攻击效果逐渐提高,当n=N时,攻击为无损失攻击。
2.2 光学攻击的表象矩阵理论对于上述过程的数字实现则需要对狄拉克符号们矩阵化,因此必须选择合适的表象。考虑量子力学表象变换,对于给定表象F,其基矢定义为|i〉,根据表象变换理论下算符和量子态与矩阵的对应关系, 在给定表象F下,算符
记:明文空间所选取的表象为|p〉,密文空间选取的表象为|q〉。对于明文-密文对|ϕi〉、|ψi〉有
| $ \left\{\begin{array}{l} \boldsymbol{\beta} = \langle q \mid \beta\rangle, \boldsymbol{\psi}_{i} = \left\langle q \mid \psi_{i}\right\rangle, \\ \boldsymbol{\alpha} = \langle p \mid \alpha\rangle, \boldsymbol{\phi}_{i} = \left\langle p \mid {\phi}_{i}\right\rangle. \end{array}\right. $ | (11) |
其中: β,ψi为|β〉,|ψi〉在密文空间表象q下的列向量; α,ϕi为|α〉,|ϕi〉在明文空间表象p下的列向量。
在数值模拟中,如matlab2019b的运行环境,可以依靠reshape函数实现将二维图像一维化,以及更高维的矩阵二维化过程。
| $ \boldsymbol{\beta} = \left[\begin{array}{ccccc} b_{11} & b_{12} & \cdot & \cdot & b_{1 n} \\ b_{21} & b_{22} & & & \\ \cdot & & \cdot & & \\ \cdot & & & \cdot & \\ b_{n 1} & & & & b_{n n} \end{array}\right] \Rightarrow \left(\begin{array}{c} b_{11} \\ b_{21} \\ \cdot \\ \cdot \\ b_{n 1} \\ b_{12} \\ b_{22} \\ \cdot \\ \cdot \\ b_{n 2} \\ \cdot \\ \cdot \\ b_{1n} \\ b_{2n} \\ \cdot \\ \cdot \\ b_{n n} \end{array}\right). $ |
算符
| $ \langle q \mid \beta\rangle = \langle q|\hat{G}| \alpha\rangle = \langle q|\hat{G}| p\rangle\langle p \mid \alpha\rangle . $ | (12) |
有
| $ \boldsymbol{G}_{q p} = \langle q|\hat{G}| p\rangle. $ | (13) |
此即为算符
| $ \left\{\begin{array}{l} \langle q \mid \beta\rangle = \langle q|\hat{G}| p\rangle\langle p \mid \alpha\rangle, \\ \left\langle q \mid \psi_{i}\right\rangle = \langle q|\hat{G}| p\rangle\left\langle p \mid \phi_{i}\right\rangle . \end{array}\right. $ | (14) |
即
| $ \left\{\begin{array}{l} \boldsymbol{\beta} = \boldsymbol{G}_{q p} \boldsymbol{\alpha}, \\ \boldsymbol{\psi}_{i} = \boldsymbol{G}_{q p} \boldsymbol{\phi}_{i}. \end{array}\right. $ | (15) |
同理,有ci=〈ψj|β〉在给定表象下的矩阵形式为
| $ \boldsymbol{C} = \boldsymbol{\varPsi}_{N}{}^{+} \boldsymbol{\beta}. $ | (16) |
其中:ΨN=(ψ1, ψ2,…,ψN),为一N×N方阵。在选择了子空间之后,待破解密文在给定表象下的子空间投影表达形式为
| $ \boldsymbol{C}_{n} = \boldsymbol{\varPsi}_{n}{}^{+} \boldsymbol{\beta}. $ | (17) |
其中: Ψn=(ψ1, ψ2,…,ψn)为一N×n矩阵,其中ψi=〈q|ψi〉。破解的明文近似解则为
| $ \left|\alpha_{\|}\right\rangle = \sum\nolimits_{i = 1}^{n} c_{i}\left|\phi_{i}\right\rangle . $ | (18) |
2007年,Frauel等[13]在分析4F系统的安全性时曾经指出对DRPE系统的攻击过程可以用一个矩阵运算刻画:C=TP。其中P代表选择明文构成的矩阵,T代表加密过程对应的矩阵,C代表选择明文对应的密文构成的矩阵。通过求解T的逆矩阵可以实现对系统的攻击。“事实上,这个方法不是很有用,因为它需要巨量的选择明密文对。举个例子,如果明文有100像素×100像素,那么攻击者需要10 000个明密文对才能重建T矩阵。”[13]遗憾的是,他们指出的仅仅是我们之前提到的利用明密文空间的一组对应的完备基直接构建逆矩阵的无损攻击方法,并且忽略了DRPE系统的幺正性。当C和P的列向量分别构成密文和明文空间的一组幺正基时,利用子空间投影的方法可以依靠很少的选择明密文对构造出一个待破解密文的近似解。
值得一提的是,在相同的子空间投影攻击结果下,选择明文的数量本质上并不与明文的像素数相关,而是与明文图像的稀疏度(或者局部稀疏度)相关。对于生活中的真实图像,往往都是可压缩的,其稀疏度数量级往往远小于图片的真实像素数,如一个文字图片或者一个二维码,往往可以拥有很大的像素数,但是其稀疏度往往只在几十到几百的数量级。这个猜想会在后面的模拟中得到验证。
3 模拟结果与分析为了验证上述理论的正确性,我们在Matlab2019b,i7-6700HQ CPU(2.60 GHz) 和16 GB内存的环境下做了如下数值模拟。
3.1 无损攻击待攻击的加密系统为含3块相位板的菲涅尔域三随机相位加密系统,结构如图 3所示,每步衍射距离均为5 cm,相位板结构参数与明文相同,加密所用波长为473 nm。

|
Download:
|
| 图 3 加密系统结构图示 Fig. 3 Structure of the encryption system | |
选择复振幅图像——Lena作为振幅,狒狒作为相位的128像素×128像素作为待破解的明文,如图 5(a)所示,采样间隔为5.5 μm。
选择16 384个脉冲作为选择明文探针,进行逐像素曝光,记录下对应的密文,利用密文重建加密矩阵ΨN=(ψ1,ψ2,…,ψN),代入式(16)和式(18)。攻击结果如图 4(b)所示。攻击结果中,振幅与相位和原图像的相关性系数均分别严格等于1。可见,当选择明文数量与像素数相同时,选择明文构成明文空间完备基,攻击结果无损。

|
Download:
|
| 图 4 无损攻击、子空间投影的有损攻击和局部区域攻击的结果展示 Fig. 4 Results of lossless attack, lossy subspace projection attack, and attack on area of interest | |
选择相同的加密系统,以及相同的待破解明文,各个结构参数不变。选择明文选择4像素×4像素的脉冲, 如图 4(c)所示。从左上到右下,依次相邻选择1 024个不同的探针进行曝光,记录下对应的密文利用密文重建加密矩阵Ψn=(ψ1,ψ2,…,ψn),代入式(16)和式(18)。攻击结果如图 4(d)所示。攻击结果中,振幅部分和原图像振幅的相关性系数达到0.864 5,相位部分和原图像相位的相关性系数达到0.815 0。从结果可以看出,攻击结果展示了原始图片粗略的轮廓,整体上是可以辨认的。且由于重建过程是按照选择明文的线性叠加进行重建,与无损攻击做对比,可以看出选择明文数量与攻击效果直接正相关。
3.3 局域子空间攻击利用子空间投影法还可以针对性的攻击某个黑客感兴趣的区域。如图 4(e)所示,待破解明文为400像素×400像素的Lena——狒狒复振幅图像中嵌套128像素×128像素的狒狒——Lena图像,采样间隔为5.5 μm,加密系统各结构参数不变。图中中部的小区域是黑客感兴趣的部分。在感兴趣区域选择1 024个脉冲探针作为选择明文,每个探针为2像素×2像素的方形脉冲,记录下对应的密文,利用密文重建加密矩阵Ψn=(ψ1,ψ2,…,ψn),代入式(16)和式(18)。攻击结果如图 4(f)所示。对于感兴趣的局部区域,攻击结果中振幅部分和原始图像对应区域的振幅部分相关性达到0.778 7,相位部分和原始图像中对应区域的相位部分相关性达到0.873 0。可见,对于有用信息的部分,子空间投影的方法获得了很好的效果。
3.4 彩色攻击对于彩色图像,其不过是三色RGB的组合,每个色彩分量独立满足线性幺正条件。在三色波长已知的情况下(一般可以通过分析密文获得),可以实现彩色攻击。待破解明文为256像素×256像素彩色图片,采样间隔为5.5 μm选择波长为红色:λ1=700 nm、绿色:λ2=546.1 nm以及蓝色:λ3=435.8 nm。选择纯振幅的彩色图像,加密系统及各结构参数不变,其输入彩色明文如图 5(a)所示。

|
Download:
|
| 图 5 彩色明文和其子空间投影法的攻击结果 Fig. 5 RGB picture as plaintext input and its attack result | |
选择1 024个脉冲探针,每个探针为8像素×8像素,采样间隔为5.5 μm。攻击结果如图 5(b)所示。攻击结果中,三色通道分别与原图中的相关性为:R: 0.884 7, G: 0.873 6, B: 0.818 9.
4 结论与扩展上述工作很好地验证了幺正线性系统在面对子空间投影法的攻击时的不安全性,而这种不安全性对应于攻击时黑客选择的方案拥有很大的自由度,而这种自由度均是系统的“幺正性”赋予的。进一步地,子空间投影方法颠覆传统上认为“增大系统像素可以使系统更加安全的认识”,因为利用这种方法,攻击的效果和选择明文的数量直接相关,而这两者都是黑客可以根据自己的需求自主选择的。在狄拉克符号的部分,以及之后的数值模拟,我们均默认选择了位置表象,事实上,选择其他表象也可以获得甚至更佳的攻击效果,而联系不同表象的矩阵自然对应于量子力学表象变换的理论。最后,对于子空间投影的方法可以扩展到已知明文攻击,其攻击效果在目前优于深度学习所得的效果。
| [1] |
Refregier P, Javidi B. Optical image encryption based on input plane and Fourier plane random encoding[J]. Optics Letters, 1995, 20(7): 767-769. Doi:10.1117/12.217669 |
| [2] |
Situ G H, Zhang J J. Double random-phase encoding in the Fresnel domain[J]. Optics Letters, 2004, 29(14): 1584-1586. Doi:10.1364/ol.29.001584 |
| [3] |
Unnikrishnan G, Joseph J, Singh K. Optical encryption by double-random phase encoding in the fractional Fourier domain[J]. Optics Letters, 2000, 25(12): 887-889. Doi:10.1364/ol.25.000887 |
| [4] |
Singh H, Yadav A K, Vashisth S, et al. Fully phase image encryption using double random-structured phase masks in gyrator domain[J]. Applied Optics, 2014, 53(28): 6472-6481. Doi:10.1364/ao.53.006472 |
| [5] |
Liu Z J, Guo Q, Xu L, et al. Double image encryption by using iterative random binary encoding in gyrator domains[J]. Optics Express, 2010, 18(11): 12033-12043. Doi:10.1364/oe.18.012033 |
| [6] |
Carnicer A, Montes-Usategui M, Arcos S, et al. Vulnerability to chosen-cyphertext attacks of optical encryption schemes based on double random phase keys[J]. Optics Letters, 2005, 30(13): 1644-1646. Doi:10.1364/ol.30.001644 |
| [7] |
Li T, Shi Y S. Security risk of diffractive-imaging-based optical cryptosystem[J]. Optics Express, 2015, 23(16): 21384-21391. Doi:10.1364/oe.23.021384 |
| [8] |
霍裕平, 杨国桢, 顾本源. 用光学方法实现幺正变换及一般线性变换(Ⅰ): 可能性的分析[J]. 物理学报, 1975, 24(6): 438-447. |
| [9] |
霍裕平, 杨国桢, 顾本源. 用光学方法实现幺正变换及一般线性变换(Ⅱ): 用迭代法求解[J]. 物理学报, 1976, 25(1): 31-46. |
| [10] |
霍裕平. 用光学方法实现么正变换及一般线性变换(Ⅲ): 优化方法及有关问题[J]. 物理学报, 1978, 27(5): 487-495. |
| [11] |
霍裕平. 用光学方法实现么正变换及一般线性变换(Ⅳ): 图形识别及投影算子[J]. 物理学报, 1980, 29(2): 153-160. |
| [12] |
杨国桢, 顾本源. 用振幅-相位型全息透镜实现光学变换的一般理论[J]. 物理学报, 1981, 30(3): 414-417. |
| [13] |
Frauel Y, Castro A, Naughton T J, et al. Resistance of the double random phase encryption against various attacks[J]. Optics Express, 2007, 15(16): 10253-10265. Doi:10.1364/oe.15.010253 |
 2022, Vol. 39
2022, Vol. 39 


