近年来,随着世界范围内的能源危机日趋严重,受控核聚变技术受到越来越多的关注。经过数十年的发展,磁约束聚变技术已经取得了突破性的进展,但在科学和技术上仍然存在许多问题亟待解决,面对等离子体材料的选择就是其中之一。目前主流的面向等离子体材料包括碳、铍、钨等[1]。然而,实验表明这些材料都在一定程度上存在难以克服的缺陷,包括物理化学溅射、力学性能退化、氚滞留等一系列问题[2-3]。相比固体材料,液态锂第一壁现已在很多磁约束核聚变装置上被证实具有独特的优势,不仅可以解决大部分固体第一壁所面临的问题,同时还可以显著提高芯部等离子体的约束性能[4-5]。
然而,作为具有一定化学活性的碱金属,液态锂对大部分金属材料都具有强烈的腐蚀作用,其中包括各种不锈钢材料,而不锈钢是目前核聚变实验装置中最常用的回路结构材料。因此,液态锂与铁基合金的相容性研究就显得尤为必要。实际上,早在20世纪80年代,人们就已经认识到液态锂可以作为聚变装置中的氚增殖材料,因而提出使用液态锂作为聚变堆包层中的冷却流体,并在随后开展了大量关于液态锂与包层结构材料的腐蚀实验研究[6-8]。结果表明液态锂对铁基合金的腐蚀是个复杂的物理化学过程,其主要形式包括以下3种:1)锂原子在合金中的渗透扩散;2)合金组分元素在液态锂中的溶解;3)液态锂以及杂质元素与合金组分元素之间发生化学反应生成中间产物。具体腐蚀过程受多种因素的影响,包括合金微观晶体结构、组分元素,液态锂中的杂质元素,环境温度,以及液态锂流速等[6]。显然,3种形式的腐蚀过程都会改变材料的微观结构,从而引起材料宏观力学性能的变化。Popovich等[9]对液态锂腐蚀前后的纯铁进行了单向拉伸试验,结果表明腐蚀后其拉伸强度和韧性都显著降低,降低程度与温度和应变率有关,当温度为400℃,应变率为0.0027/s时,纯铁拉伸强度下降接近15%,断裂应变下降85%,表现出典型的脆化效应。Chopra和Smith[10]开展了铁素体钢HT-9在液态锂中的疲劳实验,结果表明腐蚀可弱化材料的晶界,进而导致材料疲劳寿命的显著降低。Mustari和Takahashi[11]使用由316L不锈钢制成的波纹管在液态锂中进行低周疲劳实验,在断裂后的试件内同时观察到晶界裂纹和穿晶裂纹,表明液态锂的腐蚀不仅对晶界有削弱作用,同时对晶粒内部也有破坏作用。但是,受客观条件的限制,目前的实验研究仅能给出实验现象,尚不能很好地揭示腐蚀和材料损伤演化的动态过程和微观机理。
分子动力学(molecular dynamics, MD)方法是从原子尺度上对材料进行动态数值模拟的方法,对于揭示材料损伤演化的微观机理具有显著优势,目前已被广泛应用于多种材料相互作用的动态模拟研究。例如Webb等[12]模拟铅液滴在铜表面的动态铺展过程,解释了不同晶格取向对铺展速度的影响规律。Palafox-Hernandez等[13]通过计算应力、势能、扩散系数、密度等参数,证实液态铅在不同的铜晶面上具有不同的合金化行为。然而,针对液态锂对铁基合金的腐蚀问题,由于缺乏相应的原子间相互作用势函数,相关研究尚不多见。Gan等[14]开发了基于改进分析型嵌入原子法(modified analytical embedded atom method, MAEAM)理论的铁锂势函数,使得对液态锂腐蚀铁基合金的大规模分子动力学模拟成为可能。
基于液态锂腐蚀铁基合金的工程问题,本文借助Gan等[14]发展的铁锂势函数,对含锂的单晶铁在单向拉伸载荷作用下的动态响应进行大规模分子动力学模拟,重点考察锂原子的存在对铁晶体弹塑性力学行为的影响规律。
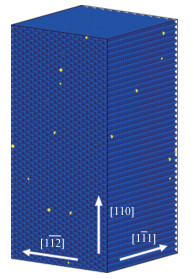
1 模型和方法采用MD方法,对具有bcc晶体结构的铁素体(α-Fe)沿<110>晶向的单轴拉伸过程进行数值模拟。模型初始晶向分别为x-[111]、y-[112]和z-[110],载荷沿z轴方向。模型初始尺寸为“17a×18a×42a”,其中a=0.2855nm为α-Fe的晶格常数[15],共包含102816个原子。为避免尺寸效应,在3个方向上均采用了周期性边界条件。通过随机替换Fe原子的方式,构建5种不同浓度的Fe-Li置换固溶体,Li原子数分数分别为0、0.05%、0.1%、0.2%和0.3%。图 1所示为0.3% Li的置换结果。由于在Li原子的分布和原子初始速度的设定上采用了随机原则,为消除随机性的影响,针对每个Li原子数分数分别进行3次独立的模拟,并将3次模拟结果的平均值作为最终结果。
|
Download:
|
| 蓝色和黄色分别表示Fe原子和Li原子 图 1 随机置换Li原子数分数为0.3%的α-Fe的初始构型 Fig. 1 Initial configuration of α-Fe with 0.3% random substitutional Li atoms | |
所有的模型都首先在等温等压系综下采用Nose-Hoover热浴法驰豫50 ps,并确保系统能量已趋于稳定。温度取为室温300 K,压力为0,时间步长1 fs。
拉伸载荷的施加通过在每个时间步内对所有原子沿拉伸方向(z轴)的坐标根据设定的应变率进行调整来实现,并在加载过程中保持其他2个方向的压力为0,受分子动力学模拟尺度的限制,应变率取为5×108/s。
系统的应力利用Virial定理[16]进行计算,其具体公式为
| $ {\mathit{\boldsymbol{\sigma }}^{ab}} = \frac{1}{\mathit{\Omega }}\left\{ { - \sum\limits_i {{m_i}} v_i^av_i^b + \frac{1}{2}\sum\limits_i {\sum\limits_{j \ne i} {\left( { - \frac{1}{{{\mathit{\boldsymbol{r}}_{ij}}}}\frac{{\partial U}}{{\partial {\mathit{\boldsymbol{r}}_{ij}}}}} \right)} } r_{ij}^ar_{ij}^b} \right\}. $ |
其中:上标a和b为笛卡尔分量,σab表示全局应力张量,Ω为系统体积,rij为原子i和j之间的相对位置向量,其第a个分量用rija表示,mi和vi分别表示原子i的质量和速度。在拉伸过程中,系统的全局应力每1ps计算一次,并且在0.5ps时间范围内进行平均。应变公式为(l-l0)/l0,其中l0和l分别表示模拟盒子长度的初始值和瞬时值。
在前期工作中,我们完全采用Gan等[14]开发的铁锂势函数进行分子动力学模拟,结果表明该势函数并不能很好地描述α-Fe晶体中位错等缺陷的动态演化过程。因此,为了获得更加准确的结果,改用由Mendelev等[15]开发的EAM势函数来模拟Fe-Fe之间的相互作用,采用Nichol和Ackland[17]开发的EAM势函数模拟Li-Li之间的相互作用,这2个势函数已经被证实可以很好地处理单晶α-Fe和单晶Li中的缺陷。Fe-Li之间的相互作用则由Gan等[14]的MAEAM势来描述。
本文使用LAMMPS软件[18]进行MD模拟,使用OVITO软件[19]进行原子构型可视化,采用公共近邻分析方法(common neighbor analysis, CNA)[20]识别系统中的缺陷,同时配合位错提取算法(dislocation extraction algorithm,DXA)[21]进行位错识别。
2 结果与讨论 2.1 应力-应变曲线图 2展示了不同Li原子数分数下的典型应力-应变曲线,可以看到在拉伸的初始阶段,应力与应变呈线性关系。随着应变的进一步增大,应力应变关系表现出明显的非线性效应。这种非线性效应是由于在单晶体中不存在位错、晶界等缺陷,材料的本构关系主要由原子间的相互作用决定,通常都具有非线性特性,类似的现象在实验[22]和模拟[23]中都有被观察到。

|
Download:
|
| 图 2 不同Li原子数分数下的应力-应变曲线 Fig. 2 The stress-strain curves at different Li atomic fractions | |
通过拟合线弹性阶段(应变范围[0, 0.03])内的应力-应变曲线,可以得到不同Li原子浓度下的杨氏模量,结果列于表 1。从表中可以看出,我们计算的纯α-Fe的杨氏模量平均值为195.7GPa,与文献[24]中的MD模拟结果187GPa非常接近,验证了我们模拟过程的可靠性。至于含Li原子的α-Fe晶体的杨氏模量,目前尚无可靠数据可用来比较。我们的计算结果显示杨氏模量受Li原子数分数的影响并不明显,最大相差仅为4.1%。从图 2也可以看到,不同Li原子数分数下的应力-应变曲线在弹性阶段内几乎重合。然而,屈服应力受Li原子数分数的影响相对比较明显,具体分析在2.3节进行。
|
|
表 1 不同Li原子数分数下<110>晶向α-Fe的杨氏模量 Table 1 The Young's moduli of <110>orientated α-Fe at different Li atomic fractions |
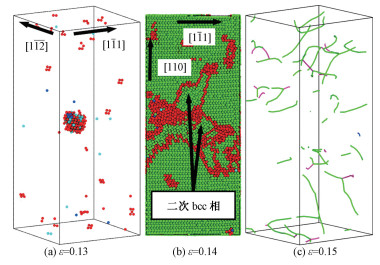
图 3所示为纯α-Fe晶体屈服后的原子构型,从图中可以看出,晶体的屈服是由bcc与hcp之间的相变所控制。当应力达到临界值时,球形的hcp团簇开始在晶体内成核,如图 3(a)所示。随着载荷的增加,hcp团簇在晶体内部迅速扩展,当hcp团簇的尺寸增大到一定程度,边界上的应力不足以维持hcp结构,随即hcp团簇发生破裂,局部的hcp结构重新变回bcc结构,同时伴随着大量位错的产生。图 3(b)中显示了晶体内局部的由hcp原子转变而来的二次bcc相。当继续增大载荷时,晶体的塑性变形主要由位错的运动支配,图 3(c)所示为应变达到0.15时晶体内部的复杂位错线分布。这种应力驱动的相变过程与DFT(第一性原理)的结果[25]保持一致。
|
Download:
|
| (a)和(b)中的原子根据CNA着色,其中绿色、蓝色、天蓝色和红色分别代表bcc、fcc、hcp和未知结构原子;(c)中绿色、紫色和蓝色线分别表示1/2<111>、<100>和<110>位错;为了清晰(a)中的bcc原子被隐藏 图 3 纯α-Fe在拉伸中的原子构型 Fig. 3 Atomic configurations of pure α-Fe during tension | |
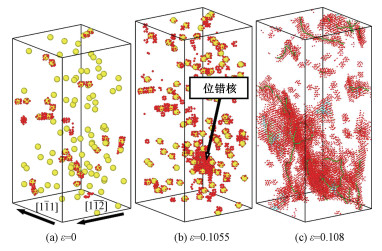
Li原子的引入对晶体的塑性变形行为具有显著的影响。图 4所示为Li原子数分数为0.1%的模型在拉伸载荷作用下的变形过程。从图 4(a)中可以看出,置换Li原子使得所在Fe晶格发生了一定的变形,部分Fe原子在CNA分析中被识别为非bcc原子。图 4(b)和4(c)为塑性变形初期的原子构形,可以看出,相变几乎已经被完全压制,位错成为塑性变形的主导机制。
|
Download:
|
| (a)和(b)中的黄色原子是放大的Li原子,其他所有原子的着色方案和图 3相同;为了显示位错线(c)中原子被缩小,位错线着色方案和图 3相同 图 4 含0.1%Li原子的α-Fe拉伸过程中的原子构型 Fig. 4 Atomic configurations of α-Fe with 0.1% Li atoms during tension | |
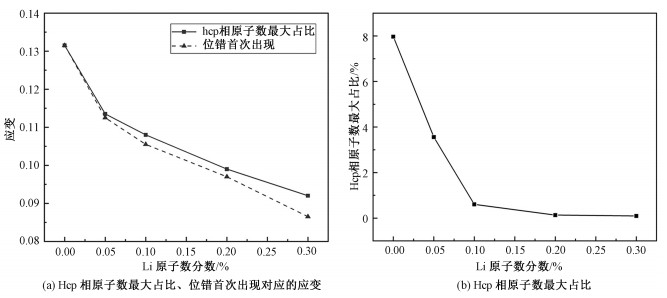
图 5(a)所示为不同Li原子数分数模型中的hcp原子数达到最大占比、位错首次出现对应的应变。Hcp原子数量达到最大占比的时刻,对应于hcp团簇破裂的瞬间。从图中可以看出,随着Li原子数分数的增加,hcp团簇破裂时的应变逐渐减小,产生位错的应变也逐渐减小。此外,对于不含Li原子的纯α-Fe晶体,位错的出现与hcp团簇的破裂几乎同时发生,而一旦引入Li原子,位错的出现则明显先于hcp团簇的破裂。这一现象说明,Li原子的存在促进了位错的形成,而位错的滑动一方面释放了晶体内的应力,导致应力驱动的bcc到hcp的相变无法持续发展;另一方面,位错与hcp团簇的相互作用,导致团簇的提前破裂。因此,随着Li原子数分数的增加,位错变得越来越容易产生,hcp团簇的体积也越来越小,如图 5(b)所示。
|
Download:
|
| 图 5 不同Li原子数分数下hcp相原子数达到最大占比、位错首次出现对应的应变,以及hcp相原子数最大占比 Fig. 5 The strain corresponding to the peak ratio of hcp atoms and the first occurrence of dislocation and the peak ratio of hcp atoms at different Li atomic fractions | |
因此,可以得出结论,置换Li原子显著抑制bcc到hcp的相变,随着Li原子数分数的增加,α-Fe晶体的塑性变形逐渐由位错支配。
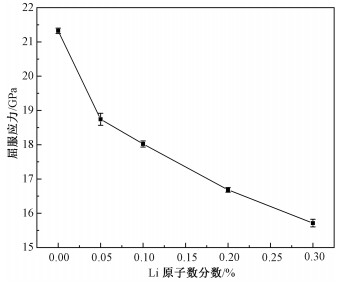
2.3 屈服应力 2.3.1 Li原子数分数的影响本文中的屈服应力取为应力-应变曲线上弹性阶段应力的峰值,对应着相变或位错产生时的应力。图 6所示为屈服应力随Li原子数分数的变化曲线。随着Li原子数分数增加,屈服应力呈单调减小趋势,即使只存在0.05%浓度的Li原子时,屈服应力仍然出现了大幅度的减小,当浓度达到0.3%时减小幅度已经达到26.3%。这一结果与Popovich[9]的实验结果一致,即Li原子的存在可以显著降低α-Fe的强度。
|
Download:
|
| 图中误差条为标准差, 后文相同 图 6 不同Li原子数分数下的屈服应力 Fig. 6 Yield stress at different Li atomic fractions | |
Li原子导致屈服应力减小的原因可以从两个方面来解释。一方面,Li原子的引入增加了缺陷潜在成核位点的数量,而这被认为是影响屈服应力的一个重要因素[26-27]。另一方面,虽然Li的密度比α-Fe小得多,但是实际上Li原子的半径比Fe原子半径更大,这种原子尺寸上的不匹配,导致在Li原子周围产生局部应变场,势能增加,Fe-Fe之间的键能强度降低,导致位错更容易发生,在宏观上表现为屈服应力变小。这种原子尺寸不匹配可以用尺寸因子来衡量,按Hepburn等[28]的定义,溶质原子X的尺寸因子为ΩSF=ΔV/Vave,其中ΔV表示用一个溶质原子X置换一个溶剂原子所引起的体积变化,Vave表示每个溶剂原子的平均体积。查阅文献可知Li原子在α-Fe中的尺寸因子ΩSF为7.5%[29],意味着置换Li原子在α-Fe晶格中实际上起着膨胀作用,这无疑会使Li原子周围的原子的内应变能增加,导致只需更少的机械变形就可使它们在热振动中离开平衡位置,进而引起屈服。
2.3.2 Li原子分布的影响本文中Li原子在α-Fe晶体中随机分布,通过仔细观察原子构形可发现,即使在低Li原子数分数的晶体中也存在彼此非常靠近的Li原子。为了考察Li原子的分布规律对屈服应力的影响,我们在引入Li原子时,限制任意2个Li原子的间距不小于3a,这个距离超过了Li原子相互作用的截断半径。为叙述简便,这里将Li原子分布被约束的系统称为约束随机分布,而无约束的系统称为完全随机分布。
两种分布的屈服应力随Li原子数分数的变化如图 7所示。可以清楚地看到,当Li原子的分布被约束时,其屈服应力相对未被约束时大幅增加,这表明邻近Li原子比单个Li原子会造成更大的屈服应力降低。这其实并不难理解,因为从直观上说邻近Li原子会引起更严重的局部晶格畸变,而晶格的变形必然引起Fe原子之间键能的变化,从而导致位错更容易产生。此外,约束随机分布屈服应力的Li浓度敏感性也显著降低,具体表现为随着Li原子数分数增加屈服应力减小的速率明显小于完全随机分布。对于完全随机分布,在较低Li浓度下邻近Li原子出现的概率较低,所以数量较少。但随着Li原子数分数增加,邻近Li原子越来越有可能形成,数量也随之增加。因此,在完全随机分布中Li浓度在很大程度上决定了邻近Li原子的数量,最终显著影响屈服应力。相反,由于完全不存在彼此非常靠近的Li原子,约束随机分布的屈服应力在任何Li浓度下都完全受单个Li原子控制,因此Li浓度的影响相对较小。

|
Download:
|
| 图 7 不同Li原子分布下的屈服应力 Fig. 7 Yield stress under different Li atom distributions | |
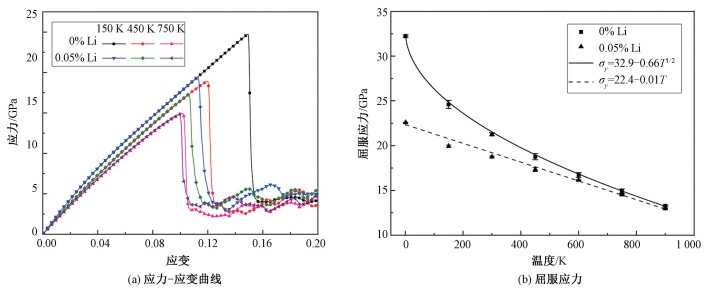
已有的研究结果显示,许多fcc和bcc金属晶体的屈服应力都表现出显著的温度依赖性,一般趋势为屈服应力随着温度的升高而减小,但是减小的规律与材料性质有关,最常见的两种规律分别是σy~T1/2和σy~T,其中σy和T分别为屈服应力和温度[30-31]。为了研究温度对Fe-Li固溶体屈服应力的影响,我们在1~900K温度范围内分别对纯α-Fe和Li原子数分数为0.05%的晶体进行了拉伸模拟。图 8(a)展示了两种晶体在不同温度下典型的应力-应变曲线,可以看到随着温度的升高,两种晶体的弹性模量逐渐降低,这一点与现有的实验结果一致[32]。此外,从图中还可以看出,随着温度升高,屈服点明显前移,晶体屈服发生得越来越早。不同温度下的屈服应力变化如图 8(b)所示,在1K时纯α-Fe的屈服应力平均值为32.2GPa,与DFT计算得到的结果32.3GPa[33]保持一致。随着温度的升高,两种晶体的屈服应力都呈单调减小的趋势,这可以用简单的热力学观点来解释:温度越高,原子动能越大,热振动幅度越大,这意味着在相同载荷作用下原子更容易离开其平衡位置,产生塑性变形。
|
Download:
|
| 图 8 不同温度下的应力-应变曲线和屈服应力 Fig. 8 The stress-strain curves and yield stress at different temperatures | |
然而,两种晶体屈服应力的减小规律却表现出了不同之处。如图 8(b)所示,纯α-Fe的屈服应力拟合曲线为σy=32.9-0.66T1/2,符合前文提到的σy~T1/2规律,这个结果也与文献[34]结果一致。但是,在含Li晶体中,屈服应力随温度变化却符合σy~T规律,拟合结果为σy=22.4-0.01T。实际上,材料的屈服同时由原子动能和键能决定。当温度较低时,原子动能较低,屈服应力主要受原子间的键能影响,Li原子的存在明显降低了Fe原子之间键的强度,因此屈服应力下降明显。随着温度的升高,原子的动能逐渐增加,对屈服应力的影响也越来越显著,相对而言,Li原子引起的Fe原子键能变化所带来的影响越来越小。综合起来,使得α-Fe晶体的屈服应力与温度的关系转变为线性关系。此外,从图 8(b)中还可以看出,随着温度的升高,两种晶体的屈服应力逐渐趋于一致,证实Li原子的影响越来越小。
3 结论本文使用分子动力学方法对单晶α-Fe的拉伸力学行为进行了数值模拟,分析置换Li原子对其弹塑性力学行为的影响,主要结论如下:
1) 塑性变形机理受Li原子的影响显著,在纯α-Fe中塑性变形首先由bcc到hcp的相变引起,随后由位错控制,Li原子的存在可以显著地抑制相变的发生,塑性变形主要通过位错的运动实现;
2) 屈服应力随Li原子数分数增大而单调减小,并且还会受到Li原子分布的显著影响,邻近Li原子相比单个Li原子对屈服应力影响更大;
3) 纯α-Fe和含Li原子的α-Fe晶体的屈服应力都随温度升高而减小,但是Li原子的存在改变了屈服应力与温度的具体关系。
在实际的金属材料中,具有单晶结构的比较少,通常都含有大量的晶界、位错等缺陷,这些缺陷对于材料的性能具有至关重要的作用。在未来的工作中,我们将逐步分析金属材料中的典型缺陷与Li原子的相互作用,以便对液态Li腐蚀造成的α-Fe力学性能退化有更加全面的了解。
| [1] |
Federici G, Skinner C H, Brooks J N, et al. Plasma-material interactions in current tokamaks and their implications for next step fusion reactors[J]. Nucl Fusion, 2001, 41(12): 1967-2137. Doi:10.1088/0029-5515/41/12/218 |
| [2] |
Küppers J. The hydrogen surface chemistry of carbon as a plasma facing material[J]. Surface Science Reports, 1995, 22(7/8): 249-321. |
| [3] |
Roth J, Tsitrone E, Loarer T, et al. Tritium inventory in ITER plasma-facing materials and tritium removal procedures[J]. Plasma Physics and Controlled Fusion, 2008, 50(10): 103001. Doi:10.1088/0741-3335/50/10/103001 |
| [4] |
Scotti F, Soukhanovskii V A, Bell R E, et al. Core transport of lithium and carbon in ELM-free discharges with lithium wall conditioning in NSTX[J]. Nucl Fusion, 2013, 53(8): 083001. Doi:10.1088/0029-5515/53/8/083001 |
| [5] |
Abdou M A, Team T A, Ying A, et al. On the exploration of innovative concepts for fusion chamber technology[J]. Fusion Eng Des, 2001, 54(2): 181-247. Doi:10.1016/S0920-3796(00)00433-6 |
| [6] |
Chopra O K, Tortorelli P F. Compatibility of materials for use in liquid-metal blankets of fusion reactors[J]. J Nucl Mater, 1984, 123(1-3): 1201-1212. Doi:10.1016/0022-3115(84)90241-1 |
| [7] |
Chopra O K, Smith D L. Influence of temperature and lithium purity on corrosion of ferrous alloys in a flowing lithium environment[J]. J Nucl Mater, 1986, 141(Part 2): 584-591. |
| [8] |
Flament T, Tortorelli P, Coen V, et al. Compatibility of materials in fusion first wall and blanket structures cooled by liquid metals[J]. J Nucl Mater, 1992, 191(Part A): 132-138. |
| [9] |
Popovich V V, Shtykalo I G, Chaevskii M I. Effect of lithium on the mechanical properties of armco iron[J]. Soviet Materials Science: a Transl of Fiziko-Khimicheskaya Mekhanika Materialov/Academy of Sciences of the Ukrainian SSR, 1967, 3(2): 88-93. Doi:10.1007/BF00715080 |
| [10] |
Chopra O, Smith D. Low-cycle fatigue behavior of HT9 alloy in a flowing-lithium environment[C]//Davis J W, Michel D J. Proceedings of the topical conference on ferritic alloys for use in nuclear energy technologies. State of Utah: Snowbird Press, 1984: 8.
|
| [11] |
Mustari A P A, Takahashi M. Metallurgical analysis of corroded bellows of bellow-sealed valve in lithium flow system[J]. Fusion Eng Des, 2013, 88(4): 202-208. Doi:10.1016/j.fusengdes.2013.02.003 |
| [12] |
Webb E B, Grest G S, Heine D R. Precursor film controlled wetting of Pb on Cu[J]. Phys Rev Lett, 2003, 91(23): 236102. Doi:10.1103/PhysRevLett.91.236102 |
| [13] |
Palafox-Hernandez J P, Laird B B, Asta M. Atomistic characterization of the Cu-Pb solid-liquid interface[J]. Acta Mater, 2011, 59(8): 3137-3144. Doi:10.1016/j.actamat.2011.01.053 |
| [14] |
Gan X L, Xiao S F, Deng H Q, et al. Atomistic simulations of the Fe(001)-Li solid-liquid interface[J]. Fusion Eng Des, 2014, 89(12): 2894-2901. Doi:10.1016/j.fusengdes.2014.06.018 |
| [15] |
Mendelev M I, Han S, Srolovitz D J, et al. Development of new interatomic potentials appropriate for crystalline and liquid iron[J]. Philos Mag, 2003, 83(35): 3977-3994. Doi:10.1080/14786430310001613264 |
| [16] |
Tsai D H. The virial theorem and stress calculation in molecular dynamics[J]. J Chem Phys, 1979, 70(3): 1375-1382. Doi:10.1063/1.437577 |
| [17] |
Nichol A, Ackland G J. Property trends in simple metals: an empirical potential approach[J]. Phy Rev B, 2016, 93(18): 184101. Doi:10.1103/PhysRevB.93.184101 |
| [18] |
Plimpton S. Fast Parallel Algorithms for short-range molecular dynamics[J]. J Comput Phys, 1995, 117(1): 1-19. Doi:10.1006/jcph.1995.1039 |
| [19] |
Stukowski A. Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool[J]. Model Simul Mater Sci Eng, 2010, 18(1): 015012. Doi:10.1088/0965-0393/18/1/015012 |
| [20] |
Honeycutt J D, Andersen H C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters[J]. J Phys Chem, 1987, 91(19): 4950-4963. Doi:10.1021/j100303a014 |
| [21] |
Stukowski A, Bulatov V V, Arsenlis A. Automated identification and indexing of dislocations in crystal interfaces[J]. Model Simul Mater Sci Eng, 2012, 20(8): 085007. Doi:10.1088/0965-0393/20/8/085007 |
| [22] |
Hagen A B, Snartland B D, Thaulow C. Temperature and orientation effects on the deformation mechanisms of α-Fe micropillars[J]. Acta Mater, 2017, 129: 398-407. Doi:10.1016/j.actamat.2017.03.006 |
| [23] |
Feng Y X, Shang J X, Qin S J, et al. Twin and dislocation mechanisms in tensile W single crystal with temperature change: a molecular dynamics study[J]. Phys Chem Chem Phys, 2018, 20(26): 17727-17738. Doi:10.1039/C8CP03241F |
| [24] |
Molnar D, Binkele P, Hocker S, et al. Atomistic multiscale simulations on the anisotropic tensile behaviour of copper-alloyed alpha-iron at different states of thermal ageing[J]. Philos Mag, 2012, 92(5): 586-607. Doi:10.1080/14786435.2011.630690 |
| [25] |
Friák M, Šob M. Ab initio study of the bcc-hcp transformation in iron[J]. Phys Rev B, 2008, 77(17): 174117. Doi:10.1103/PhysRevB.77.174117 |
| [26] |
Zhu T, Li J, Samanta A, et al. Temperature and strain-rate dependence of surface dislocation nucleation[J]. Phys Rev Lett, 2008, 100(2): 025502. Doi:10.1103/PhysRevLett.100.025502 |
| [27] |
Zuo L, Ngan A H W. Molecular dynamics study on compressive yield strength in Ni3Al micro-pillars[J]. Phil Mag Lett, 2006, 86(6): 355-365. Doi:10.1080/09500830600803890 |
| [28] |
Hepburn D J, MacLeod E, Ackland G J. Transition metal solute interactions with point defects in fcc iron from first principles[J]. Phys Rev B, 2015, 92(1): 014110. Doi:10.1103/PhysRevB.92.014110 |
| [29] |
Devi E A, Chinnappan R, Sundar C S. First-principles study of interaction energies of atomic defects in bcc ferromagnetic iron[J]. Phys Rev B, 2018, 98(14): 144104. Doi:10.1103/PhysRevB.98.144104 |
| [30] |
Weinberger C R, Cai W. Plasticity of metal nanowires[J]. Journal of Materials Chemistry, 2012, 22(8): 3277-3292. Doi:10.1039/c2jm13682a |
| [31] |
Rabkin E, Nam H S, Srolovitz D J. Atomistic simulation of the deformation of gold nanopillars[J]. Acta Mater, 2007, 55(6): 2085-2099. Doi:10.1016/j.actamat.2006.10.058 |
| [32] |
Adams J J, Agosta D S, Leisure R G, et al. Elastic constants of monocrystal iron from 3 to 500 K[J]. J Appl Phys, 2006, 100(11): 113530. Doi:10.1063/1.2365714 |
| [33] |
Černý M, Šesták P, Pokluda J. Strength of bcc crystals under combined shear and axial loading from first principles[J]. Comp Mater Sci, 2012, 55: 337-343. Doi:10.1016/j.commatsci.2011.11.009 |
| [34] |
Kotrechko S, Ovsjannikov A. Temperature dependence of the yield stress of metallic nano-sized crystals[J]. Philos Mag, 2009, 89(33): 3049-3058. Doi:10.1080/14786430903179554 |
 2022, Vol. 39
2022, Vol. 39 

