无人机(unmanned aerial vehicle)的自主导航(autonomous navigation)问题在近年来备受关注。要实现自主导航,关键是要进行合理的运动规划(motion planning),这也是移动机器人的热门研究领域。根据是否储存并使用全局地图进行导航,运动规划可以分为全局规划和局部规划。
全局规划方法已经被广泛地研究,通常做法是通过感知全局环境建立一张地图,然后寻找一条最优路径,该路径可避免碰撞并到达目标点,最后通过路径跟踪(path following)控制移动机器人沿路径行至目标点,这类方法也被称之为路径规划(path planning)[1]。常见的路径规划算法包括基于节点搜索的方法[2],基于快速搜索随机树的方法[3-4],以及基于人工势场的方法[5-6]。因为需要存储并处理全局地图以进行导航,全局规划方法一般只能工作在有限的空间范围。根据是否预先已知全部障碍物信息,全局规划可以大体上分为离线规划和在线规划。离线规划在已知全局环境的情况下,直接预先计算出从起点到目标点的路径。而在线规划在初始阶段可能不知道或者仅知道部分环境信息,在机器运动过程中,当检测到新的环境信息或已知环境发生改变时,更新其储存的全局地图,并动态地重新规划出新的路径。很多研究是在传统离线规划算法的基础上进行改进,提出在线规划变体[7-8]。另外,还有一些研究在环境未知的条件下,采用一边进行构建全局地图,一边根据已有地图进行导航的方法,进而把问题转化成为已知环境的路径规划问题。然而,这类方法不仅需要精度较高的传感器,也需要较多的前期探索和地图构建时间,难以普适不同场景环境。
局部规划方法则不使用通用的全局地图,而是直接使用传感器实时获取的环境信息,或者一个活动窗口范围内的环境信息,进行快速的避障反应并指引机器向目标点运动,有些研究者称之为实时避障(real-time obstacle avoidance)。局部规划不需要预先规划出一条完整路径,而是可以随时改变导航的起点和目标点。对环境信息的感知往往是依靠测距传感器,比如声呐、激光雷达、深度相机等,获取其到周围障碍物的距离。传统的实时避障方法有虚拟力场法[9]、向量直方图法[10]等。此外,一些模糊逻辑类的方法[11]、遗传算法类的方法[12]和基于学习的方法[13]也被提出。因为只需要有限的信息进行导航,不无限积累历史环境信息,其工作的空间范围理论上不受限制,而代价则是在某些特殊情况下可能无法找到可行的路径。此外,有些研究使用多层规划结合的方法实现自主导航,在顶层使用粗粒度的全局路径规划计算出路径点以保证可达性,在底层则使用局部规划从一个路径点到下一个路径点,从而得到更为平滑的路径[14]。
无人机作为一种特殊的移动机器人,在通用的导航方法之上,又有一些特殊性。关键在于无人机不仅运动速度相对较快,且对碰撞更为敏感,一旦发生碰撞不仅很容易损坏机器,更可能失速坠落造成不必要的人身伤害和财产损失。除此之外,无人机的工作环境也往往不同于普通的地面机器人。上文提到的很多方法最早是基于地面机器人提出的,它们一般以路径最短作为最优指标[1]。对无人机导航来说,更需要保证飞行中的安全,不应仅仅为了路程更短以致于太靠近障碍物,而是需要在路径长度和远离障碍上进行均衡,人工势场法天然具备这一个优点。然而传统人工势场法可能会由于局部极小点的存在使无人机陷入其中。很多研究以不同的方式尝试解决这个问题,其中,基于拉普拉斯方程(Laplace’s equation)和调和函数(harmonic function)的方法较为成功地解决了这个问题[15-16]。该方法利用拉普拉斯方程的解——调和函数不存在局部极小值的特性,通过构建调和函数的人工势场,避免陷入局部极小值。通过求解拉普拉斯方程建立的势场叫做拉普拉斯人工势场,或简称拉普拉斯势场。
我们之前的工作也是基于拉普拉斯势场,并使用边界元法(boundary element method,BEM)进行求解,实现了已知全局地图的无人机避障导航[17]。对于大型势场来说,边界元法求解效率相对较高。与之前工作不同的是,本文主要针对未知环境,提出基于拉普拉斯势场的局部规划方法,因所求势场较小,有限差分法(finite difference method,FDM)完全可以胜任,且其实现简单,易于并行实现,故本文使用有限差分法求解势场。该导航方法仅基于传感器的实时探测数据,随着无人机的移动,不断建立新的局部拉普拉斯势场,从而指引无人机向目标点运动,实现实时避障导航:
1) 根据传感器探测信息,建立一个网格化的局部地图表示的边值问题,其解即为拉普拉斯势场。该方法可以灵活地应对各种形状大小各异的障碍物。
2) 采用有限差分法求解上述边值问题,该方法是用于数值求解边值问题的常用方法,通过迭代更新网格中的值,直至收敛。
3) 随着传感器数据的更新,随时更换新的势场并求解。而在更换势场过程中仍然可以随时提供场内任意一点的参考速度。
4) 使用MATLAB实现并仿真了基于PID的无人机控制器,根据机身所在位置获得参考速度方向后,控制器控制无人机跟踪参考方向,最终无人机在导航算法指引下飞向目标点。
本文将拉普拉斯人工势场的思想应用到局部地图上。仿真实验表明,该方法计算简洁快速,没有复杂的参数调试,可以自如应对各种不同的环境和障碍物,能够适用于未知环境中的实时导航。
1 基于拉普拉斯方程的人工势场 1.1 拉普拉斯方程与边值问题人工势场法[18]最早由Khatib于1986年提出,其基本思想是在可行的工作空间上建立合适的势函数,使移动机器人沿着势函数的负梯度方向进行运动,也可以近似看作是沿着势函数的流线(streamline)进行运动。传统的人工势场法对障碍物建立排斥势函数,对目标点建立吸引势函数,然后进行代数叠加得到合势函数。这种势函数可能产生局部极小值,使得无人机被困住。由拉普拉斯方程定义的调和函数因具有无局部极值的良好特性,可以巧妙地解决这个问题。
拉普拉斯方程是有着如下形式的二阶偏微分方程
| $ \Delta \phi=\sum\limits_{i=1}^{n} \frac{\partial^{2} \phi}{\partial x_{i}^{2}} \equiv 0. $ | (1) |
其中:n是自变量的维度,Δ称作拉普拉斯算子。该方程的解ϕ被称作调和函数。
调和函数有很多良好的性质,比如调和函数是实解析的[19],因此也是无穷阶可导(光滑)的。另外一个良好性质,被称作强最大值/最小值原理[19],表述如下:
定理1(强最大值/最小值原理) 设Ω是非空区域(连通的开集称为区域或开区域), ϕ是在Ω上调和的实函数, 若ϕ在Ω上有最大值/最小值,则ϕ为常数函数。
根据上述定理和调和函数的实解析性质,可以推导出局部极大值/极小值原理:
定理2 (局部极大值/极小值原理) 设Ω是非空区域,ϕ是在Ω上调和的实函数,若ϕ在Ω上有局部极大值/极小值,则ϕ为常数函数。
也就是说,若Ω有界,则非常数的调和函数ϕ,其全局的最大值与最小值只能出现在Ω的边界上,且在Ω内部没有局部极值。
仅通过上述偏微分方程是无法唯一确定一个解的。一个微分方程及其边界上的约束条件就构成了边值问题。最早研究的以及最为人熟知的边值问题是狄利克雷问题(Dirichlet problem),就是要找出满足狄利克雷边界条件的拉普拉斯方程的解,其定义如下:
定义 (狄利克雷问题) 考虑定义在
二维的狄利克雷问题可以如下表示
| $ \frac{\partial^{2} \phi(x, y)}{\partial x^{2}}+\frac{\partial^{2} \phi(x, y)}{\partial y^{2}}=0, \quad \forall(x, y) \in \varOmega, $ | (2) |
| $ \phi(x, y)=f(x, y), \quad \forall(x, y) \in \partial \varOmega . $ | (3) |
根据最大值/最小值原理,可以证明狄利克雷问题的解的唯一性[19]。研究表明,当边界足够光滑时,狄利克雷问题总有解[20]。而本文中对于整个定义域包括边界,都进行了网格化表示,可以将其看作另一个有着足够光滑边界的狄利克雷问题的离散近似,并且通过数值求解方法,总是可以求得一个数值解。
本文基于二维的拉普拉斯方程,通过设置有界区域的边界值,构建出一个狄利克雷问题,其区域边界上的值可以唯一确定一个满足约束的调和函数。该调和函数表示的人工势场,即拉普拉斯势场,其负梯度方向被用来作为避障导航的参考方向。
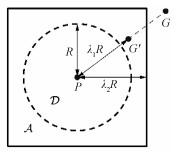
1.2 狄利克雷问题的构建本文所述的测距传感器并不特定于某种具体的传感器,只要可以实时探测到自身到周边障碍物的距离即可,其侦测范围也被设定在水平面上。在仿真中,直接使用射线进行交点计算:以自身为中心向四周发射射线,然后返回到命中点(射线与障碍物的交点)的距离。设传感器对一圆周进行n等角抽样,则抽样间隔为2π/n弧度。传感器安装在无人机机身上,本文将传感器和无人机作为同一质点。设传感器的最大可探测距离为R,则无人机的可探测范围是一个圆面
为构建一个狄利克雷边值问题,需要首先确定地图范围和选取临时目标点。在一开始,目标点很可能在局部地图的范围之外。因此,需要先选定一个临时目标点,以指引无人机向正确的方向飞行。设局部地图涵盖的所有区域为
| $ G^{\prime}=P+\lambda_{1} R \frac{G-P}{\|G-P\|} \in \mathcal{A}, \quad \lambda_{1}>1 . $ | (4) |
局部地图范围应该覆盖所有探测点和临时目标点。因此,以当前点P为中心,以a=2λ2R为边长,取λ2>λ1,形成的正方形区域
| $ \mathcal{A}=\left\{(x, y)\left|\left| x-x_{0}\right|\leqslant \frac{a}{2},\left| y-y_{0} \right| \leqslant \frac{a}{2}\right.\right\}, $ | (5) |
即为局部地图范围,如图 1所示。
|
Download:
|
| 图 1 狄利克雷问题的构建 Fig. 1 The construction of Dirichlet problems | |
下一步则是确定势场函数的边界及其边界值。为实现局部势场的导航,有如下约束条件:
1) 避免与障碍物发生碰撞。因此,障碍物应该作为势场边界且固定为最大值M,否则势场中的势值可能大于障碍物的势值,使无人机与障碍物发生碰撞。
2) 避免无人机飞出局部地图。因此,局部地图的边界需要作为势场的边界且固定为最大值M,否则,无人机很可能在负梯度方向的指引下倾向于飞出局部地图边界。
3) 引导无人机趋近临时目标点。因此,临时目标点应该作为势场边界并固定为最小值m,只有这样,势场函数的流线才会汇聚于临时目标点。
最终,势场函数的边界值由以上3部分组成。其中传感器探测的结果是很多个点,这些障碍点可以根据实际情况、离散间隔等适当扩充为稍大的区间或者圆面。本文因为进行网格化时的分辨率较低,并未进行扩充。
本文选取λ1=1.1,λ2=1.2,M=1,m=0。值得注意的是,因为计算机求解的时候是网格化进行的,如果格数太少,可能使得目标方向的最远探测点、临时目标点和局部地图边界点出现重合,这时候应该调整λ1和λ2使之落在不同的格子里,并且最好有些间隔。
1.3 拉普拉斯人工势场的数值求解拉普拉斯方程是最简单的椭圆微分方程之一,其数值求解方法主要包括:有限差分法、有限元法、边界元法。本文采用有限差分法进行数值求解,因其实现简单,且网格化的方式非常有利于将探测到的障碍点以及目标点等直接放置在局部地图中。
有限差分法的基本思想是把连续问题离散化,以差分替代微分,将微分方程及其约束条件转化为只包含有限个未知量的差分方程组,并将该差分方程组的解作为原问题的近似离散解。首先,将整个局部地图网格化为等间隔的网格节点。本文将正方形地图的每个方向都等分为n个区间,则区间长度为h=a/n,得到纵向网格线x=xi=x0+ih和横向网格线y=yj=y0+jh,其中i, j=0, 1, …, n。网格线的交点(xi, yj)被称为网格点,其势函数值表示为ϕi, j。然后,将拉普拉斯算子离散化,以中心差分公式来近似偏微分,可得
| $ \left.\frac{\partial^{2} \phi}{\partial x^{2}}\right|_{i, j} \approx \frac{\phi_{i+1, j}-2 \phi_{i, j}+\phi_{i-1, j}}{h^{2}}, $ | (6) |
| $ \left.\frac{\partial^{2} \phi}{\partial y^{2}}\right|_{i, j} \approx \frac{\phi_{i, j+1}-2 \phi_{i, j}+\phi_{i, j-1}}{h^{2}} . $ | (7) |
根据拉普拉斯方程的定义,可以得到
| $ \frac{\phi_{i+1, j}+\phi_{i-1, j}+\phi_{i, j+1}+\phi_{i, j-1}-4 \phi_{i, j}}{h^{2}}=0, $ | (8) |
化简为
| $ 4 \phi_{i, j}-\left(\phi_{i+1, j}+\phi_{i-1, j}+\phi_{i, j+1}+\phi_{i, j-1}\right)=0 . $ | (9) |
将区域中的每个非边界网格点的函数值ϕi, j作为未知变量,对它们分别应用式(9),可以得到一个大型的稀疏线性方程组。该方程组的系数矩阵对角线值均为4,且每一行都有不超过4个-1,其余元素均为0。该线性方程组的解构成了以网格值表示的拉普拉斯势场。
求解线性方程组的迭代解法有雅克比法和高斯赛德尔法等。通过运用雅克比法求解该线性方程组,则求解过程实际上等同于将每一个非边界网格点更新为其上、下、左、右4个网格点的平均值,即
| $ \phi_{i, j}^{k+1}=\frac{\phi_{i-1, j}^{k}+\phi_{i+1, j}^{k}+\phi_{i, j-1}^{k}+\phi_{i, j+1}^{k}}{4}, $ | (10) |
其中k为迭代的循环变量。如此循环往复,直至收敛。运用高斯赛德尔法求解相当于类似的过程,不同的是其对每一个点的更新都当场生效,更新所需的4个相邻点的值均使用目前的最新值。假设i和j的遍历顺序都是从小到大,高斯赛德尔法可以表示为
| $ \phi_{i, j}^{k+1}=\frac{\phi_{i-1, j}^{k+1}+\phi_{i+1, j}^{k}+\phi_{i, j-1}^{k+1}+\phi_{i, j+1}^{k}}{4} . $ | (11) |
可以证明,对于连通区域的有限差分方法,雅克比法和高斯赛德尔法可以保证收敛[21]。高斯赛德尔法收敛速度是雅克比法的2倍,但是雅克比法的优点是在一次迭代中各点更新互相独立,更容易在GPU上并行实现。本文的仿真部分采用高斯赛德尔法进行数值求解。
1.4 势场梯度的数值求解因为对局部地图进行网格化,可以直接使用周围相邻网格点进行数值微分求得梯度。对于任一网格点(xi, yj),由中心差分公式得到该点的近似梯度为
| $ \nabla \phi_{i, j}=\left[\begin{array}{l} \left.\frac{\partial \phi}{\partial x}\right|_{i, j} \\ \left.\frac{\partial \phi}{\partial y}\right|_{i, j} \end{array}\right] \approx\left[\begin{array}{l} \frac{\phi_{i+1, j}-\phi_{i-1, j}}{2 h} \\ \frac{\phi_{i, j+1}-\phi_{i, j-1}}{2 h} \end{array}\right] . $ | (12) |
对于在网格线但不是网格点的坐标点,可以进行线性插值来近似该点的梯度。例如,对于横向网格线y=yj上的点(x, yj),计算出h整除x-x0的商
| $ \nabla \phi\left(x, y_{j}\right) \approx \frac{1}{h}\left((h-\alpha) \nabla \phi_{i, j}+\alpha \nabla \phi_{i+1, j}\right), $ | (13) |
得出该点的近似梯度,纵向网格线上的点同理。对于不在网格线上的点,可以进行双线性插值来近似该点的梯度。首先,计算h整除x-x0的商
| $ \begin{gathered} \nabla \phi(x, y) \approx \frac{1}{h}\left((h-\alpha) \nabla \phi\left(x_{i}, y\right)+\right. \\ \left.\alpha \nabla \phi\left(x_{i+1}, y\right)\right) \approx \frac{1}{h^{2}}\left((h-\alpha)(h-\beta) \nabla \phi_{i, j}+\right. \\ (h-\alpha) \beta \nabla \phi_{i, j+1}+\alpha(h-\beta) \nabla \phi_{i+1, j}+ \\ \left.\alpha \beta \nabla \phi_{i+1, j+1}\right), \end{gathered} $ | (14) |
求得该点的近似梯度。网格点和网格线的情况均可看作双线性插值的特例,可以直接使用式(14)实现。
2 无人机控制器设计与仿真 2.1 基于梯度场的速度跟踪根据求解得到的拉普拉斯势场可以计算出一条到目标点的流线。虽然可以直接对该流线进行路径跟踪,但是在真实环境中的误差和干扰下,该方式对于实时避障不太友好。本文采用拉普拉斯势场的负梯度方向作为参考速度方向。结合设定的速率值s,得到参考水平速度vd,然后通过速度跟踪控制(tracking control),使无人机调整自身状态,并将其水平速度收敛于参考值。之所以仅使用负梯度的方向,是因为拉普拉斯势场是由边值问题解出来的,而不是手动定义出来的,其梯度的大小对导航而言无意义,只需要按照负梯度的方向飞行即可实现避障与趋近目标点。根据求得的梯度值,无人机处于点P=(xP, yP) 时的参考水平速度即为
| $ \boldsymbol{v}_{d}^{P}=-s \frac{\nabla \phi\left(x_{P}, y_{P}\right)}{\left\|\nabla \phi\left(x_{P}, y_{P}\right)\right\|}. $ | (15) |
本文仅考虑水平面的二维导航,在仿真实验中采用恒定速率的定高飞行。需要指出的是,根据本文控制器的设计,速率s和参考高度zd均可以在飞行过程中随时进行更改设置。由于本文提出的局部导航方法仅使用由实时传感器数据构建的局部地图,并不需要一张全局地图,因此高度的变化并不影响导航。而水平速率的设置也不影响导航本身,只要无人机可以保持稳定和安全即可。另外旋翼的物理限制也可能导致在过大倾角的情况下难以维持高度。但是这些和导航算法本身无关,总而言之,参考速率和参考高度的变化对导航本身影响不大。
2.2 控制器设计与仿真实现本文使用基于PID的控制器对无人机进行导航控制仿真实验。下文使用的相关符号如表 1所示。需要注意的是,欧拉角是在旋转过程中以中间坐标系定义的,而角速度是统一以机身坐标系衡量的,因此,欧拉角的导数并不等于角速度。
|
|
表 1 控制系统符号表 Table 1 Symbols of the control system |
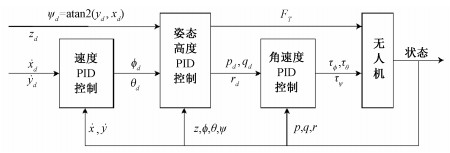
整个系统分为控制器和无人机系统模型2部分,系统的外部输入为参考水平速度
|
Download:
|
| 图 2 无人机控制系统 Fig. 2 The UAV control system | |
无人机的全局坐标系采用NED坐标系,即3个坐标轴正方向依次指向北、东、下。本文使用下列经典的无人机运动学及动力学模型[22-23]进行仿真计算:
| $ \left[\begin{array}{c} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{array}\right]=\left[\begin{array}{c} \left(-\left(C_{\phi} C_{\psi} S_{\theta}+S_{\phi} S_{\psi}\right) F_{T}-K_{d x} \dot{x}\right) / m \\ \left(-\left(C_{\phi} S_{\psi} S_{\theta}-C_{\psi} S_{\phi}\right) F_{T}-K_{d y} \dot{y}\right) / m \\ \left(-\left(C_{\phi} C_{\theta}\right) F_{T}-K_{d z} \dot{z}\right) / m+g \end{array}\right], $ | (16) |
| $ \left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right]=\left[\begin{array}{ccc} 1 & S_{\phi} T_{\theta} & C_{\phi} T_{\theta} \\ 0 & C_{\phi} & -S_{\phi} \\ 0 & S_{\phi} / C_{\theta} & C_{\phi} / C_{\theta} \end{array}\right]\left[\begin{array}{c} p \\ q \\ r \end{array}\right], $ | (17) |
| $ \left[\begin{array}{c} \dot{p} \\ \dot{q} \\ \dot{r} \end{array}\right]=\left[\begin{array}{c} \left(\left(J_{y}-J_{z}\right) q r+\tau_{\phi}\right) / J_{x} \\ \left(\left(J_{z}-J_{x}\right) p r+\tau_{\theta}\right) / J_{y} \\ \left(\left(J_{x}-J_{y}\right) p q+\tau_{\psi}\right) / J_{z} \end{array}\right], $ | (18) |
其中: C、S、T为三角函数的简写。该模型考虑了惯性和空气阻力,并进行部分简化。因为我们是离散地实现控制系统,在一个时间片长度内,可以认为这些变量是常数,由此计算出其他状态量。为简明起见,没有模拟状态观测,而是直接将状态的真值反馈给各控制器。
3 实验仿真与分析 3.1 势场求解本文提出的局部导航方法主要分为势场求解和势场中任意点的梯度求解。其中梯度求解使用固定数量的节点进行中心差分和双线性插值,其时间复杂度为常数。而求解势场的计算时间主要在于使用高斯赛德尔方法求解FDM。高斯赛德尔方法的时间复杂度为O(ln2),其中n为未知数的数量,l为迭代次数。不过根据上文所述,由于待求解线性方程组是稀疏的,每个待求解变量的单次更新都是常数时间,因此求解势场的时间复杂度为O(ln)。本文将求解区域离散化为N×N的格子,则总的未知数数量约为n=O(N2)。故总的时间复杂度为O(lN2),其中N为局部地图一个维度上的离散格子数量。
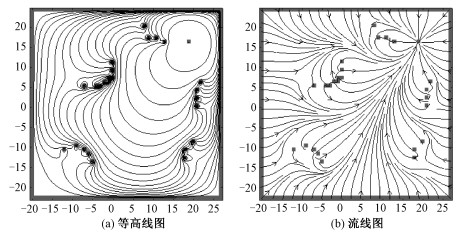
本文设定无人机传感器的最大探测距离R为20 m,按照1 m间隔进行网格化,结合前文所述的λ2=1.2,最终得到48×48的局部地图网格。某单个局部势场的等高线图和流线图如图 3所示,其中灰色格子为势场的边界点,包括地图边界、探测到的障碍点和目标点。
|
Download:
|
| 图 3 拉普拉斯人工势场 Fig. 3 Laplacian potential field | |
这里等高线和流线均采用双线性插值进行计算,且图中等高线的值并不是均匀的。从图中可以看出,障碍物和局部地图边界就是最高值的等高线,而目标点处为最低值的等高线,各个起点的流线均流向目标点。
3.2 避障导航前文分别介绍了拉普拉斯势场的构建和控制器的设计与实现。事实上,实际应用中的这2个模块可以是同时进行、互不干扰的。导航模块负责根据接收到的最新传感器探测信息求解势场,而控制模块从导航模块获取参考方向,生成参考速度,从而控制无人机飞行。在求解新势场的时间内,参考方向仍然从之前的势场中获取,一旦新的势场求解出来则立即更换,之后参考方向就从新的势场中获取了。势场的更新频率主要取决于传感器探测效率和解算势场时的计算效率。本文使用MATLAB仿真时,设定势场的更新频率为1 Hz,而控制频率为100 Hz,无人机质量m =1.4 kg,测距传感器在水平面对圆周进行60°等角抽样探测。进行仿真实验的计算机使用Intel(R) Core(TM) i7-8850 H CPU,主频2.60 GHz。
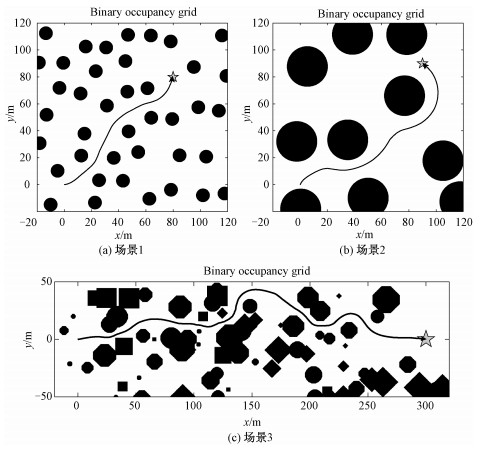
本文采用3个不同的场景进行实验,图 4展示了这些场景下的仿真实验结果。3个场景中障碍物的位置均为随机生成,起点均设为(0, 0)。其中场景1是较多的小障碍物,目标点设为(80, 80);场景2是面对几个大障碍物的情况,目标点设为(90, 90);场景3则是更长距离的飞行,目标点设为(300, 0),该场景中障碍物大小不一、形状各异、疏密不同,且通过重叠黏连形成了不规则的障碍物。在这3个场景中,我们统一设定水平速率为1 m/s。从图中可以看到,无人机在躲避障碍物的情况下,顺利到达了图中以五角星标记的目标点。无人机的运动路径既没有特别绕远,也没有为趋近目标点而与障碍物过近或擦边,而是在趋近目标点的同时,尽可能在障碍物间隙的中间走,即到周边各障碍物的距离较为均衡。
|
Download:
|
| 图 4 MATLAB仿真实验路径图 Fig. 4 The path results in MATLAB simulations | |
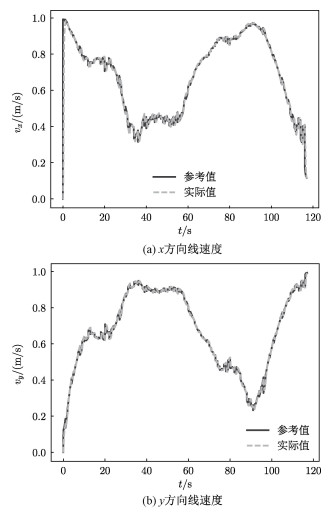
本文控制器部分直接对水平速度的2个正交分量进行跟踪控制,为观察控制器的跟踪效果,以图 4中的场景1为例,整个飞行过程中无人机水平线速度的参考值和实际值如图 5所示,其中深灰色实线为参考值,浅灰色虚线为实际值(下同)。从图中可以看到,控制器能及时响应参考速度的变化。
|
Download:
|
| 图 5 速度的跟踪控制 Fig. 5 The tracking control of velocity | |
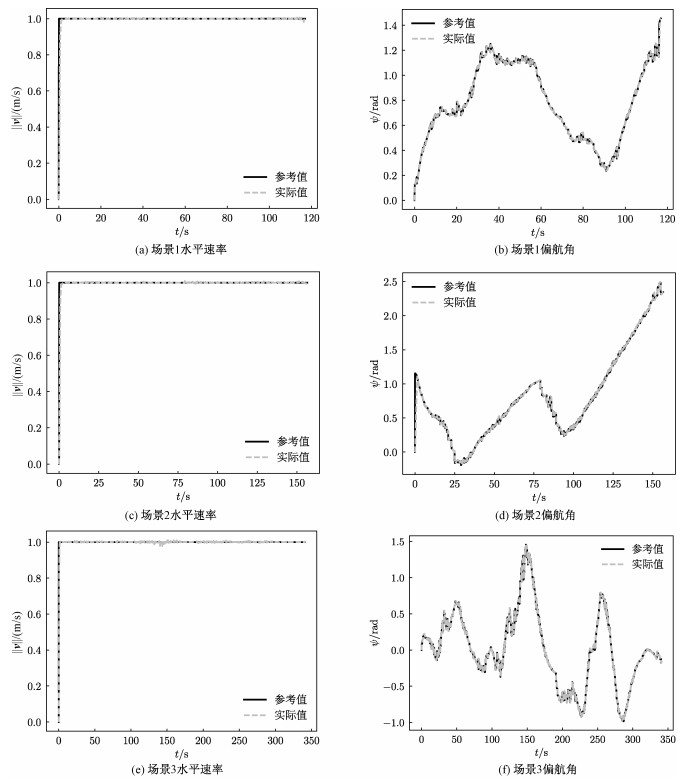
3个场景中无人机的水平速率和偏航角如图 6所示。从图中可见,3个场景中无人机速率基本维持设定值,偏航角整体上变化平稳。在前2个场景中,水平速率几乎没有变化,偏航角也只有局部轻微抖动,而场景3因为障碍物较多,频繁改变方向,使得维持恒定速率相对更加困难,偏航角的局部抖动较前2个场景稍多稍大,但整体上也没有产生巨大突变。偏航角的抖动主要来自于势场的更换,由于探测信息的变动和无人机的运动,使得势场的构成和目标点的选取发生变化,求解得到的新的势场和原势场在同一点就可能产生不同的参考方向。这种轻微的抖动是可以接受的,也是无人机根据新的信息调整方向的表现。另外,从图中可以看出,控制器通过对速度分量的跟踪,使得偏航角也紧紧跟随着参考值,可以快速响应参考方向的变化。
|
Download:
|
| 图 6 水平速率和偏航角 Fig. 6 Horizontal speeds and yaw angles | |
经过统计,场景1从起点到目标点,总共运行了11 737个控制周期,根据本文控制频率100 Hz的设定,这相当于飞行了117.37 s。其中总共解算了118个局部拉普拉斯势场,使用高斯赛德尔法求解的平均迭代次数为897.559 3(计整个局部地图迭代一遍为1次),且迭代收敛次数的标准差为155.440 7,从拿到传感器数据到求解出拉普拉斯势场的平均时间为0.020 7 s,标准差为0.003 3 s。从该结果可以看出,达到收敛所需的迭代次数比较一致,且求解时间较快,完全满足实时要求,可以接受最快约48.3 Hz的传感器信息更新频率。至于获取梯度,只需对周围几个点进行差分和插值,所用时间可以忽略不计。
4 结论本文提出基于局部拉普拉斯人工势场的无人机实时避障导航,该方法有以下特点:
1) 仅使用实时传感器信息构建局部边值问题,采用有限差分法求解拉普拉斯人工势场,该势场可以适应各种形态大小各异的障碍物。调和函数的良好特性使得势场内部不存在局部极小点,且势场梯度连续光滑使导航轨迹平稳。
2) 随着传感器信息的更新,重新计算并替换拉普拉斯势场,控制部分始终使用最新解出的势场获取无人机当前点的参考方向,并将其结合设定的速率计算出参考速度,以进行速度的跟踪控制。
3) 设计并实现基于PID的控制系统,并使用MATLAB进行仿真实验以验证该导航方法。
仿真实验显示,该方法在不同外界环境下,可以较为平滑地避开障碍物并趋向目标点。最终的轨迹不仅总体较短,而且尽可能地保持了到各障碍物距离的均衡,导航更为安全。该方法具有较好的实时性,可以应用到现实场景中。
| [1] |
Yang L, Qi J T, Song D L, et al. Survey of robot 3D path planning algorithms[J]. Journal of Control Science and Engineering, 2016, 2016: 7426913. Doi:10.1155/2016/7426913 |
| [2] |
Meng B B, Gao X G. UAV path planning based on bidirectional sparse A* search algorithm[C]//2010 International Conference on Intelligent Computation Technology and Automation. May 11-12, 2010, Changsha, China. IEEE, 2010: 1106-1109. DOI: 10.1109/ICICTA.2010.235.
|
| [3] |
Lavalle S M. Rapidly-exploring random trees: a new tool for path planning[R]. Ames, IA, USA: Iowa State University, 1998.
|
| [4] |
Karaman S, Frazzoli E. Optimal kinodynamic motion planning using incremental sampling-based methods[C]//49th IEEE Conference on Decision and Control. December 15-17, 2010, Atlanta, GA, USA. IEEE, 2010: 7681-7687. DOI: 10.1109/CDC.2010.5717430.
|
| [5] |
Shi P, Zhao Y W. Global path planning for mobile robot based on improved artificial potential function[C]//2009 IEEE International Conference on Automation and Logistics. August 5-7, 2009, Shenyang, China. IEEE, 2009: 1900-1904. DOI: 10.1109/ICAL.2009.5262656.
|
| [6] |
Gao Y, Wei Z Q, Gong F X, et al. Dynamic path planning for underwater vehicles based on modified artificial potential field method[C]//2013 Fourth International Conference on Digital Manufacturing Automation. June 29-30, 2013, Shinan, China. IEEE, 2013: 518-521. DOI: 10.1109/ICDMA.2013.122.
|
| [7] |
Karaman S, Walter M R, Perez A, et al. Anytime motion planning using the RRT*[C]//2011 IEEE International Conference on Robotics and Automation. May 9-13, 2011, Shanghai, China. IEEE, 2011: 1478-1483. DOI: 10.1109/ICRA.2011.5980479.
|
| [8] |
Otte M, Frazzoli E. RRTX: asymptotically optimal single-query sampling-based motion planning with quick replanning[J]. The International Journal of Robotics Research, 2016, 35(7): 797-822. Doi:10.1177/0278364915594679 |
| [9] |
Borenstein J, Koren Y. Real-time obstacle avoidance for fast mobile robots[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1989, 19(5): 1179-1187. Doi:10.1109/21.44033 |
| [10] |
Borenstein J, Koren Y. The vector field histogram-fast obstacle avoidance for mobile robots[J]. IEEE Transactions on Robotics and Automation, 1991, 7(3): 278-288. Doi:10.1109/70.88137 |
| [11] |
Montaner M B, Ramirez-Serrano A. Fuzzy knowledge-based controller design for autonomous robot navigation[J]. Expert Systems with Applications, 1998, 14(1/2): 179-186. Doi:10.1016/S0957-4174(97)00059-6 |
| [12] |
Lei L, Wang H J, Wu Q S. Improved genetic algorithms based path planning of mobile robot under dynamic unknown environment[C]//2006 International Conference on Mechatronics and Automation. June 25-28, 2006, Luoyang, China. IEEE, 2006: 1728-1732. DOI: 10.1109/ICMA.2006.257475.
|
| [13] |
Motlagh O, Nakhaeinia D, Tang S H, et al. Automatic navigation of mobile robots in unknown environments[J]. Neural Computing and Applications, 2014, 24(7/8): 1569-1581. Doi:10.1007/s00521-013-1393-z |
| [14] |
Jin X, Gupta S, Luff J M, et al. Multi-resolution navigation of mobile robots with complete coverage of unknown and complex environments[C]//2012 American Control Conference. June 27-29, 2012, Montreal, QC, Canada. IEEE, 2012: 4867-4872. DOI: 10.1109/ACC.2012.6314800.
|
| [15] |
Connolly C I, Burns J B, Weiss R. Path planning using Laplace's equation[C]//1990 IEEE International Conference on Robotics and Automation. May 13-18, 1990, Cincinnati, OH, USA. IEEE, 1990: 2102-2106. DOI: 10.1109/ROBOT.1990.126315.
|
| [16] |
Sato K. Deadlock-free motion planning using the Laplace potential field[J]. Advanced Robotics, 1992, 7(5): 449-461. Doi:10.1163/156855393X00285 |
| [17] |
顾育津, 宋孝成, 刘晓培, 等. 基于拉普拉斯人工势场的无人机避障控制[J]. 中国科学院大学学报, 2020, 37(5): 681-687. Doi:10.7523/j.issn.2095-6134.2020.05.013 |
| [18] |
Khatib O. Real-time obstacle avoidance for manipulators and mobile robots[M]// Cox I J, Wilfong G T. Autonomous Robot Vehicles. New York, NY, USA: Springer, 1986. DOI: 10.1007/978-1-4613-8997-2_29.
|
| [19] |
Axler S, Bourdon P, Ramey W. Basic properties of harmonic functions[M]// Harmonic Function Theory: Graduate Texts in Mathematics, Vol 137. New York, NY, USA: Springer, 2001: 1-29. DOI: 10.1007/978-1-4757-8137-3_1.
|
| [20] |
Landis E M. Second order equations of elliptic and parabolic type[M]//Providence, Rhode Island, USA: American Mathematical Society, 1997. DOI: 10.1090/mmono/171.
|
| [21] |
Morton K W, Mayers D F. Numerical solution of partial differential equations: an introduction[M]. 2nd ed. Cambridge, UK: Cambridge University Press, 2005. Doi:10.1017/cbo9780511812248
|
| [22] |
Zuo Z. Trajectory tracking control design with command-filtered compensation for a quadrotor[J]. IET Control Theory & Applications, 2010, 4(11): 2343-2355. Doi:10.1049/iet-cta.2009.0336 |
| [23] |
García Carrillo L R, Dzul López A E, Lozano R, et al. Modeling the quad-rotor mini-rotorcraft[M]// Quad Rotocraft Control: Advances in Industrial Control. London, UK: Springer, 2013: 23-34. DOI: 10.1007/978-1-4471-4399-4_2.
|
 2022, Vol. 39
2022, Vol. 39 


