2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
多光谱相机具有可同时获得地物目标空间信息和光谱信息的优势,被广泛应用于地质灾害评估、农作物和环境监测以及地图测绘领域[1]。目前常见的多光谱相机根据分光原理可分为光路分光式、多镜头分离式和滤光片转轮式,这些相机大多配备复杂的机械分光设备,灵活性低。镀膜双镜头多光谱相机利用探测器单元镀膜的方式简化了多光谱相机结构,获取数据速度快且体积小重量轻,适合无人机平台搭载或手持。
多光谱影像不同波段之间的配准是航空遥感数据处理的关键步骤,影响着遥感数据产品的质量。目前图像配准方法大致可分为基于灰度、基于特征2类。基于灰度的配准方法对非线性灰度变换十分敏感,容易造成大的配准误差,因此波段配准常用适应度和通用度更强的基于特征的配准方法。目前特征配准领域应用最多的是Lowe提出的SIFT(scale invariant feature transform)算法[2],SIFT算法具有尺度、旋转不变性,定位精度高且对噪声和光照变化的容忍度高,但算法计算量较大。不少研究将SIFT算法进行改进[3-4], 提高了配准精度及效率,但仍无法满足数据量大、时效性要求高的配准场景。SIFT算法出现之后,涌现了一系列不同的局部特征配准算法,Herbert Bay提出的SURF (speeded up robust features) 算法[5]继承了SIFT算法的不变性,计算成本较SIFT减少3/4,学者们针对不同的应用场景对SURF算法进行了适应性改进,如利用颜色不变量边缘特征及颜色直方图提高SURF算法对彩色图像的配准效率[6],利用全局匹配和像元局部配准模型相结合提高SURF算法城市遥感影像配准精度[7]等。在特征快速提取方面,Rosten等[8]提出FAST算子,效率很高但不变性较差。在特征点描述方面,Michael Calonder等提出二进制描述子BRIEF(binary robust independent elementary features)算法[9],一定程度上解决了主成分分析(principal componerots analysis, PCA)等降维方法[10]无法很好解决计算描述子耗时的问题。目前计算机视觉领域应用最广泛的ORB(oriented brief)算法[11]是在FAST、BRIEF算法的基础上进行了改进,弥补了传统FAST算法不具备旋转不变性的缺点,效率较SIFT算法提高了100倍,但ORB不具备尺度不变性,不适用于涉及尺度变换的配准场景。此外,Leutenegger等提出的BRISK(binary robust invariant scalable keypoints)算法[12],Alahi等受视网膜启发提出的FREAK(fast retina keypoint)算法[13]等都大大缩短了配准时间。运用二进制描述子的ORB、BRISK、FREAK等算法虽能极大提高算法效率,但相对于传统的浮点型SIFT、SURF描述子可区分性和鲁棒性较差[14],在图像匹配的过程中易产生大量的误匹配。考虑到镀膜双镜头多光谱相机波段数目多光谱范围广,配准时涉及尺度变换的特点,本文选择对效率及鲁棒性较高的SURF算法进行改进,完成波段配准。
SURF算法能够产生大量特征点,但由于波段影像之间差异较大,配准时大规模的特征点中会存在很多无效特征点,拖慢匹配速度的同时造成误匹配。针对上述问题,本文提出一种快速版的SURF算法(F-SURF),在充分继承SURF算法不变性与鲁棒性的前提下剔除无效特征点与误匹配,增强算法的实时性。本文将介绍镀膜双镜头多光谱相机成像原理,配准前的畸变校正预处理,重点探讨F-SURF算法配准原理与流程并设计实验进行分析。
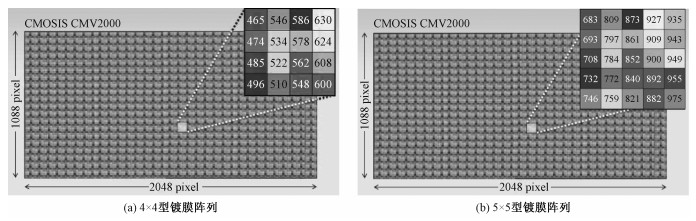
1 相机成像原理本文研究的多光谱相机利用在探测器单元上镀不同中心波长带通薄膜的方式完成分光。不同中心波长的带通薄膜按不同规格的像素矩阵排列成一个滤光单元,整齐镀在探测器上,两种镀膜阵列如图 1所示。相机拥有2套子探测系统,子探测器之间仅镀膜滤光阵列单元大小不同,外观如图 2所示。一套子探测器配备4×4型镀膜阵列负责采集波长465~630 nm范围的可见光波段。另一套配备5×5型镀膜阵列主要负责采集波长683~975 nm范围的近红外波段。相机选用CMOSIS CMV2000型探测器,数据采集速度最高可达170 cubes/s,影像覆盖可见光到近红外波段范围,可广泛应用于农林业监测、环境监测、灾害评估等领域。
|
Download:
|
| 图 1 镀膜阵列示意图 Fig. 1 Coated array of the coated multispectral camera | |

|
Download:
|
| 图 2 相机外观 Fig. 2 Appearance of the coated multispectral camera | |
子探测器采集的原始影像的分辨率均为2 048像素×1 088像素,一幅原始影像包含所有波段信息,需要根据镀膜阵列的规格,对原始影像进行采样得到单波段影像。4×4型探测器采样步长为4,采样得到16个分辨率为512像素×272像素的单波段影像。5×5型探测器采样步长为5,采样得到25个分辨率为409像素×217像素的单波段影像。
2 数字畸变模型采样畸变校正法该相机属于非量测型相机,初始配备5 mm短焦镜头,内方位元素与镜头畸变参数未知。在波段配准前需对各波段影像畸变进行校正,消除畸变对后续波段配准的影响。镀膜双镜头多光谱相机畸变校正的对象是原始影像采样后的单波段影像,不能直接利用原始影像的各项畸变参数,因此需要找到原始影像畸变与单波段影像畸变之间的关系,进而完成各波段的畸变校正。
本文采用的数字畸变模型采样法是通过数字畸变模型建立各波段影像与原始影像畸变的关系,进而实现单波段影像的校正。数字畸变模型(digital distortion model, DDM)是一种有起伏的三维几何模型,与数字高程模型(digital elevation model, DEM)形制类似,其平面坐标为数字影像行阵和列阵的编号, 高程是相应像素的总体畸变[15]。
建立单波段数字畸变模型完成畸变校正的步骤如下:
1) 利用多片后方交会法[16]分别完成2个子探测器的检校,得到各自的内方位元素和畸变系数,根据式(1)的经典畸变模型计算出子探测器原始影像每个像元的X、Y方向的畸变值大小,分别建立起原始影像的X方向和Y方向的DDM。
| $ \left\{ {\begin{array}{*{20}{l}} \begin{aligned} \Delta x =& \left( {x - {x_0}} \right)\left( {{k_1}{r^2} + {k_2}{r^4}} \right) + {p_1}\left[ {{r^2} + 2{{\left( {x - {x_0}} \right)}^2}} \right] + \\ &2{p_2}\left( {x - {x_0}} \right)\left( {y - {y_0}} \right), \end{aligned}\\ \begin{aligned} \Delta y =& \left( {y - {y_0}} \right)\left( {{k_1}{r^2} + {k_2}{r^4}} \right) + {p_2}\left[ {{r^2} + 2{{\left( {y - {y_0}} \right)}^2}} \right] + \\ &2{p_1}\left( {x - {x_0}} \right)\left( {y - {y_0}} \right), \end{aligned} \end{array}} \right. $ | (1) |
式中: (x, y)为像平面坐标; Δx, Δy为畸变差; (x0, y0, f)为内方位元素;
(k1, k2, p1, p2)为畸变系数;
2) 对各子探测器建立好的X,Y方向的2个DDM按各波段对应的像元位置进行采样,并将畸变值按采样比例缩小后即可得到各个波段影像的X方向和Y方向的DDM。4×4型子探测器从原始影像X,Y方向DDM模型中采样出各波段对应位置的畸变差,重新排列后将畸变差数值缩小为1/4得到各波段影像的X,Y方向畸变差模型,同理,5×5型子探测器单波段畸变差数值需要缩小为1/5。
3) 利用各波段DDM的畸变差值计算出各波段去畸变影像与存在畸变的各波段原始影像之间的关系,反解法求得坐标后选用双线性内插法得到畸变校正后的各波段影像。
3 SURF算法 3.1 特征点提取SURF使用的是Hessian矩阵行列式近似值图像,Hessian矩阵是SURF算法的核心[17]。设(x, y) 为图像I上某一点坐标,Hessian矩阵在尺度σ上可以表示为
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {{L_{xx}}\left( {x, y, \sigma } \right)}&{{L_{xy}}\left( {x, y, \sigma } \right)}\\ {{L_{xy}}\left( {x, y, \sigma } \right)}&{{L_{yy}}\left( {x, y, \sigma } \right)} \end{array}} \right], $ | (2) |
式中:
| $ {\rm{det}}\left( \mathit{\boldsymbol{H}} \right) = {\rm{ }}{D_{xx}}{D_{yy}} - {(0.9{D_{xy}})^2}. $ | (3) |
SURF算法用不断增大的盒子滤波器与图像卷积构建出多组多层的尺度空间。在不同的尺度图像上寻找特征点,当待定点比周围26个领域的Hessian矩阵行列式值都大或者都小时,将该待定点作为特征点,最后通过在尺度空间进行三维二次函数拟合得到特征点的准确位置。
3.2 特征点描述确定特征的主方向。以特征点为中心,计算以6 σ为半径的领域内的点在X, Y方向的Haar小波响应,并对响应值进行高斯加权,使越靠近中心特征点的点贡献率越大。滑动60°范围的窗口,计算范围内的所有响应组成的新矢量,以5°为步长遍历整个圆形邻域,选择最长矢量的方向为特征点主方向。
生成描述符。以主方向为坐标轴基准,在特征点周围取一个边长为20 σ的正方形区域。将该区域分为4×4个子区域,统计每个子区域水平方向和垂直方向的Haar小波响应值,并对其进行高斯加权。计算每个子区域所有响应值的水平、垂直方向之和以及水平、竖直方向绝对值之和,作为4个描述向量。最后生成特征点周围区域的64个向量。
3.3 特征匹配首先对所有特征点Hessian矩阵迹进行正负检测,若异号则不进行后续的相似性判断,以此加快匹配速度。对同号的特征点计算欧式距离利用最近邻比率法进行匹配,即待匹配特征点到参考图像特征点的最近距离与次近距离之比小于阈值(推荐阈值0.7),则认为该特征点与最小距离对应的特征点是最佳匹配点。
4 改进的SURF算法 4.1 优化SURF算法组数由SURF算法可知特征点匹配时需要计算64维向量之间的欧式距离,计算量庞大,因此在进行特征点匹配之前,要尽可能多地提取出能够参与最终正确匹配的有效特征点。SURF算法不同的尺度空间组数设置决定着特征点的尺度、数量规模,经典SURF算法一般采用4组的参数设置。镀膜双镜头多光谱相机41个波段虽灰度差异稍大,但图像的边缘结构等细节信息一致性较高,这些信息大多存在于图像金字塔的小尺度空间中,因此可以适当调整SURF算法的组数,尽可能多地保留待配准波段影像稳定的强特征点,剔除对正确匹配无用的特征点,提升算法效率。
利用各组特征点匹配贡献度为基准优化组数。某组特征点匹配贡献度定义为最终被判定为正确匹配的特征点中该组特征点所占比值。特征点匹配贡献度越高,说明该组提取出的有效特征点越多。表 1为配准后统计出的该新型相机多组影像的各组特征点平均匹配贡献度。实验使用组数为4的经典SURF算法对波段影像进行特征点提取,并利用RANSAC算法剔除误匹配点的方法进行配准,此处将RANSAC算法剔除误匹配后的匹配点对视为正确点对。由于2个子探测器获得的波段图像分辨率不同,因此波段配准时涉及同分辨率配准与异分辨率配准2种匹配类型,参考波段选择图像分辨率高且图像熵值最大的4×4子探测器的第7波段。
|
|
表 1 各组特征点匹配贡献度 Table 1 The matching contribution of each octave |
从表 1数据可以看出2种类型的图像配准均呈现出正确匹配点中第1组特征点占比最多,随着尺度增大,特征点对正确匹配的贡献越少的特点。同分辨率配准第1组和第2组对正确匹配贡献率合计超过95.6%,异分辨率第1组和第2组对正确匹配贡献率合计超过98%,第3组与第4组特征点对正确匹配的贡献率均不超过5%,因此可以根据新型相机图像特征及图像配准呈现的规律将SURF算法组数设置为2组,保留小尺度第1、2两组特征点。
4.2 舍弃旋转不变性简化算法同一子探测器各波段影像是从同一原始影像采样而来的,图像分辨率相同,涉及的旋转角度可以忽略不计,2个子探测器安装时严格平行且通过刚体连接,因此2个子探测器波段之间的旋转角度同样很小。由SURF算法原理可知特征点的旋转不变性是由以主方向为零方向描述关键点来保证的,若配准图像之间旋转角度很小(-15°~+15°)时,可以将SURF算子简化为不考虑旋转不变性的版本,不计算特征点主方向,直接进行后续的步骤,在提高特征点提取速度的同时不会降低匹配精度。
4.3 渐进采样一致性算法剔除误匹配引入渐进采样一致性算法(PROSAC)进行精细配准。最近邻比率法匹配后会存在较多的误匹配,大部分研究利用随机一致性算法(RANSAC)剔除误配准[19-20],能够很好地提高配准精度,但RANSAC算法稳定性低耗时高。PROSAC算法[21]是对RANSAC算法的改进,实验证明相比于RANSAC算法及其他改进算法,PROSAC算法的精度及效率有了较大的提升[22-23]。
PROSAC算法步骤如下:
1) 判断当前迭代次数是否大于设置的最大迭代次数,若是返回内点数最多的点对集,若不是则进行步骤2)。
2) 将当前匹配点对按匹配质量(最近邻比值越小质量越高)从高到低排列。
3) 选取排序在前的M个的匹配子集,从M个匹配子集中随机选取K个匹配点计算变换矩阵。遍历匹配集中所有的匹配点对,利用当前变换矩阵计算投影误差,设置投影误差阈值,小于阈值的点对则判定为内点。
4) 判断内点数目是否大于设置的最大内点数目,若是返回当前的点对集,若不是返回步骤1)完成一次迭代。
通过PROSAC算法剔除误匹配点计算变换矩阵,得到2幅图像的投影关系,将待配准图像变换到参考图像的坐标系下。本文选择单应矩阵为变换模型,图像I(x, y)与I(x′, y′)的投影关系如下
| $ \left[ \begin{array}{c} x\prime \\ y\prime \\ \mathit{1} \end{array} \right] = \mathit{\boldsymbol{H}}\left[ \begin{array}{c} x\\ y\\ \mathit{1} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{h_1}}&{{h_2}}&{{h_3}}\\ {{h_4}}&{{h_5}}&{{h_6}}\\ {{h_7}}&{{h_8}}&\mathit{1} \end{array}} \right]{\rm{ }}\left[ \begin{array}{c} x\\ y\\ \mathit{1} \end{array} \right] $ | (4) |
在相机相同的状态和模式下从4个不同方向对工业级的室内三维几何标定场进行拍摄,分别获得2个子探测器不同方位的影像。使用控制点提取软件高精度地半自动识别出原始影像的特征点坐标,采用多片后方交会法对相机进行检校,获取数字畸变模型采样法所需的各类畸变参数,表 2为多片后方交会检校结果。
|
|
表 2 相机各子探测器检校结果 Table 2 Calibration results of each camera sub-detector |
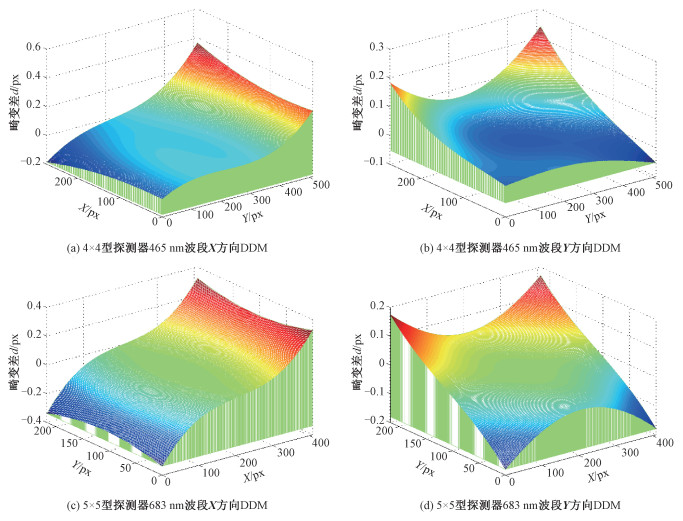
得到各子探测器的内方位元素和畸变系数后,利用上文所选定的畸变模型,计算各子探测的原始影像各像素在X、Y方向上的畸变差,完成各探测器原始影像的X、Y方向DDM的构建。对构建好的原始影像DDM按各波段位置进行采样,对畸变值按子探测器类型进行缩放,得到41个单波段影像的DDM,分别以每个子探测器的第一个波段为例展示单波段影像DDM如图 3。
|
Download:
|
| 图 3 单波段示例影像DDM Fig. 3 The DDM of single band sample image | |
4×4型探测器单波段影像(以465 nm波段为例)X方向畸变在0.4像素之内,最大畸变为0.364 7像素;Y方向畸变在0.3像素之内,最大畸变为0.239 0像素。5×5型探测器单波段影像(以683 nm波段为例)X方向畸变在0.4像素之内,最大畸变为0.340 1像素;Y方向畸变在0.2像素之内,最大畸变为0.180 9像素。从单波段影像DDM数据中可以看出该相机镜头存在一定程度的畸变,畸变会造成一定程度的像点误差,破坏正确的摄影光束形状并且会对后续的影像配准等流程产生影响。因此在处理本相机的影像时,首先利用数字畸变模型采样法对相机影像进行畸变校正,再进行波段配准的流程是合理的。
5.2 波段配准实验完成畸变校正后对去畸变的多光谱影像各波段进行配准。选择一组无人机飞行影像如图 4(a)、4(b),一组手持拍摄影像如图 4(c)、4(d)共90余对(40对同分辨率波段配准,50对异分辨率波段配准)波段影像对提出的改进的SURF算法进行验证。

|
Download:
|
| 图 4 畸变校正后的各子探测器示例单波段影像 Fig. 4 Single band image after distortion correction | |
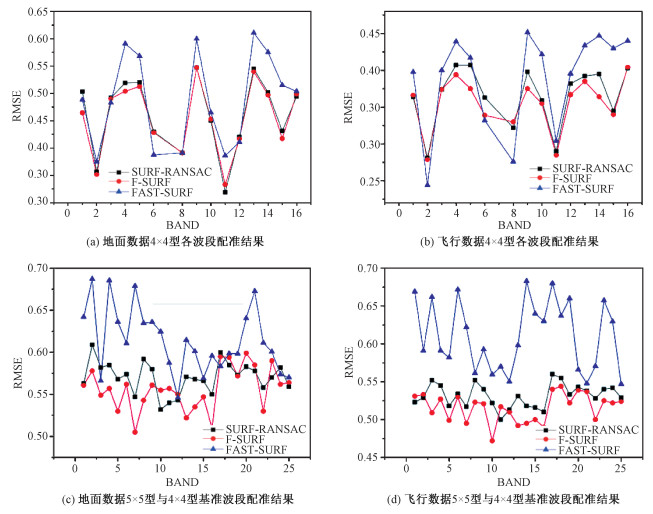
本文选择高分辨率4×4型探测器的图像熵最高的第7波段为基准影像。利用F-SURF算法完成与基准影像同分辨率4×4型剩余15个波段的配准以及与基准影像异分辨率的5×5型25个波段的配准。为了验证改进算法的有效性,进行SURF-RANSAC算法、FAST-SURF[24]快速配准方法与本文F-SURF算法的比较,由于SURF原算法没有引入剔除误匹配点的机制,导致在处理本相机多光谱波段影像时配准平均误差超过了3个像素,此处不作为实验比较对象。表 3展示了几种算法的配准效率,图 5展示了以均方根误差(root mean square error, RMSE)衡量的配准结果。
|
|
表 3 配准效率表 Table 3 Efficiency of registration |
|
Download:
|
| 图 5 波段配准RMSE Fig. 5 RMSE of band registration | |
由上述实验可看出:
1) 图 5(a)、5(b)展示了手持拍摄影像与无人机拍摄影像2组数据在同分辨率维度下4×4型探测器剩余15个波段与基准波段之间的配准结果。地面数据SURF-RANSAC算法配准平均RMSE为0.461,FAST-SURF算法为0.49,F-SURF算法为0.456;飞行数据SURF-RANSAC算法配准平均RMSE为0.366,FAST-SURF为0.388,F-SURF为0.355。在4×4型同分辨率配准时,F-SURF算法配准精度最高。
2) 图 5(a)、5(b)展示了2组数据在异分辨率维度下5×5型探测器25个波段与4×4型基准波段之间的配准结果。地面数据SURF-RANSAC算法配准平均RMSE为0.57,FAST-SURF算法为0.614,F-SURF算法为0.555;飞行数据SURF-RANSAC算法配准平均RMSE为0.531,FAST-SURF为0.61,F-SURF为0.515。对5×5型与4×4基准波段配准时,由于待配准图像与基准影像分辨率不同涉及到尺度变换,因此尺度不变性较差的FAST-SURF算法的配准精度较低。3种算法中F-SURF算法配准精度最高。
3) 对比2个类型的配准结果可以看出同分辨率波段配准精度略高于异分辨率波段配准,这是由于参与同分辨率配准的是4×4型探测器影像的15个波段(除基准波段),这15个波段与被选为基准影像的4×4型第7波段是从同一原始图像采样得来的,特征一致性高更易配准。而参与异分辨率配准波段影像是5×5型探测器波段,这25个波段与基准影像来自于不同的子探测器,波段差异较大,特征一致性较低。
从上述配准误差与配准效率数据中可以看出本文提出的F-SURF算法的配准精度优于SURF-RANSAC算法与FAST-SURF算法,在配准速度方面F-SURF算法相比于SURF-RANSAC有了较大提升,并与FAST-SURF快速配准算法效率相当。因此F-SURF算法能够更好地适用于波段多、数据量庞大的多光谱相机,保证配准精度的前提下增强数据处理及时性。
6 结论本文介绍新型镀膜双镜头多光谱相机的原理,详细探讨了其波段配准方法。首先利用数字畸变模型采样法完成单波段影像校正,消除了影像畸变对波段配准的影响;接着对畸变校正后的波段影像运用F-SURF算法进行图像配准。该算法主要从以下3个方面进行改进:特征提取方面,该算法结合相机影像特征,利用特征点匹配贡献度优化了尺度空间组数的设置;特征点描述方面,利用相机各波段影像之间旋转角度极小的特点,舍弃了原SURF算法的旋转不变性;特征点匹配方面,引入PROSAC算法剔除误匹配。实验结果表明,本文提出的波段配准处理流程和方法,在对同分辨率波段影像和异分辨率波段影像进行配准时,配准精度均远高于SURF原算法,优于经典SURF-RANSAC算法与FAST-SURF快速配准算法,并且配准效率有了较大的提升,证明本文提出的流程与方法适用于新型镀膜双镜头多光谱相机的波段配准。
| [1] |
赵英时. 遥感应用分析原理与方法[M]. 北京: 科学出版社, 2003: 38.
|
| [2] |
Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. Doi:10.1023/b:visi.0000029664.99615.94 |
| [3] |
王峰, 尤红建, 傅兴玉, 等. 应用于多源SAR图像匹配的级联SIFT算法[J]. 电子学报, 2016, 44(3): 548-554. Doi:10.3969/j.issn.0372-2112.2016.03.008 |
| [4] |
陈梦婷, 闫冬梅, 王刚. 基于Harris角点和SIFT描述符的高分辨率遥感影像匹配算法[J]. 中国图象图形学报, 2012, 17(11): 1453-1459. |
| [5] |
Bay H, Tuytelaars T, Van G L. SURF: speeded up robust features[C]//European Conference on Computer Vision-ECCV 2006. Springer, 2006: 404-417. DOI: 10.1007/11744023-32.
|
| [6] |
罗天健, 刘秉瀚. 融合特征的快速SURF配准算法[J]. 中国图象图形学报, 2015, 20(1): 95-103. Doi:10.11834/jig.20150110 |
| [7] |
孙越, 王宏琦, 李峰, 等. 面向变化检测的遥感影像弹性配准方法[J]. 武汉大学学报·信息科学版, 2018, 43(1): 53-59. Doi:10.13203/j.whugis20150510 |
| [8] |
Rosten E, Drummond T. Machine learning for high-speed corner detection[C]//European Conference on Computer Vision-ECCV 2006. Springer, 2006: 430-443. DOI: 10.1007/11744023_34.
|
| [9] |
Calonder M, Lepetit V, Strecha C, et al. BRIEF: Binary Robust Independent Elementary Features[C]//European Conference on Computer Vision-ECCV 2010. Springer, 2010: 778-792. DOI: 10.1007/978-3-642-15561-1_56.
|
| [10] |
Ke Y, Sukthankar R. PCA-SIFT: a more distinctive representation for local image descriptors[C]//IEEE Conference on Computer Vision and Pattern Recognition-CVPR 2004. June 27-July 2, 2004, Washington, DC, USA. IEEE, 2004: 511-517. DOI: 10.1109/CVPR.2004.1315206.
|
| [11] |
Rublee E, Rabaud V, Konolige K, et al. ORB: an efficient alternative to SIFT or SURF[C]// 2011 IEEE International Conference on Computer Vision. November 6-13, 2011, Barcelona, Spain. IEEE, 2011: 2564-2571. DOI: 10.1109/ICCV.2011.6126544.
|
| [12] |
Leutenegger S, Chli M, Siegwart R Y. Brisk: Binary robust invariant scalable keypoints[C]// 2011 IEEE International Conference on Computer Vision. November 6-13, 2011, Barcelona, Spain. IEEE, 2011: 2548-2555. DOI: 10.1109/ICCV.2011.6126542.
|
| [13] |
Alahi A, Ortiz R, Vandergheynst P. FREAK: Fast retina keypoint[C]// 2012 IEEE Conference on Computer Vision and Pattern Recognition June 16-21, 2012, Providence, RI, USA. IEEE, 2012: 510-517. DOI: 10.1109/CVPR.2012.6247715.
|
| [14] |
许允喜, 陈方. 局部图像描述符最新研究进展[J]. 中国图象图形学报, 2015, 20(9): 1133-1150. Doi:10.11834/jig.20150901 |
| [15] |
冯文灏, 商浩亮, 侯文广. 影像的数字畸变模型[J]. 武汉大学学报·信息科学版, 2006, 31(2): 99-103. Doi:10.3969/j.issn.1671-8860.2006.02.002 |
| [16] |
冯文灏. 近景摄影测量: 物体外形与运动状态的摄影法测定[M]. 武汉: 武汉大学出版社, 2002: 116-142.
|
| [17] |
闫敬文, 王宏志, 林哲, 等. 基于改进SURF的遥感图像目标识别[J]. 扬州大学学报(自然科学版), 2018, 21(3): 74-78. Doi:10.19411/j.1007-824x.2018.03.016 |
| [18] |
董强, 刘晶红, 周前飞. 用于遥感图像拼接的改进SURF算法[J]. 吉林大学学报(工学版), 2017, 47(5): 1644-1652. Doi:10.13229/j.cnki.jdxbgxb201705042 |
| [19] |
Hossein-Nejad Z, Nasri M. An adaptive image registration method based on SIFT features and RANSAC transform[J]. Computers & Electrical Engineering, 2016, 62: 1-14. Doi:10.1016/j.compeleceng.2016.11.034 |
| [20] |
迟英朋, 刘畅. 一种适用于SAR图像配准的改进SIFT算法[J]. 中国科学院大学学报, 2019, 36(2): 259-266. Doi:10.7523/j.issn.2095-6134.2019.02.014 |
| [21] |
Chum O, Matas J. Matching with PROSAC: progressive sample consensus[C]// 2005 IEEE Conference on Computer Vision and Pattern Recognition. June 20-25, 2005, San Diego, CA, USA. IEEE, 2005: 220-226. DOI: 10.1109/CVPR.2005.221.
|
| [22] |
Zhao P P, Ding D R, Wang Y X, et al. An improved GMS-PROSAC algorithm for image mismatch elimination[J]. Systems Science & Control Engineering, 2018, 6(1): 220-229. Doi:10.1080/21642583.2018.1477635 |
| [23] |
李振宇, 田源, 陈方杰, 等. 基于改进ORB和PROSAC的无人机航拍图像拼接算法[J]. 激光与光电子学进展, 2019, 56(23): 91-99. Doi:10.3788/LOP56.231003 |
| [24] |
产叶林, 胡新平. 基于FAST和SURF的特征点快速匹配算法[J]. 计算机工程与设计, 2019, 40(12): 3500-3504. Doi:10.16208/j.issn1000-7024.2019.12.023 |
 2022, Vol. 39
2022, Vol. 39 


