近年来，由于用户对移动数据速率的需求不断增长, 无人机(unmanned aerial vehicles, UAVs)通信技术吸引了学术界和工业界的广泛关注^[1-3]。无人机凭借体积小、易于部署等特性，为地面用户提供临时的无线通信链路来辅助传统的地面基站，以此应对某些突发事件短期内对网络资源的过度需求，例如节假日、演唱会以及灾害救援等场景。无人机和地面基站(base stations, BSs)混合部署的无人机辅助蜂窝网络系统已经被认为是一种既可以满足高速率数据需求又能够减轻传统地面基站负载的有效方法^[1]。

就无人机辅助蜂窝通信网络而言，主要的研究方向分为两类，一是充分利用无人机的灵活性，通过设计无人机的运动轨迹来提升系统性能^[4], 另一个方向则是本文所关注的内容，即利用随机几何将基站和无人机的位置建模成随机点过程，从而有效地评估系统的网络级性能指标^[5]，为无人机与地面基站的位置部署提供启示性指导。由于泊松点过程(Poisson point processes, PPP)易于处理的特性，大多数相关文献都将无人机位置建模为PPP^[6-8]。然而，在一些特定的场景下，PPP难以准确地刻画无人机的分布特性，采用其他更加合适的拓扑模型可以得到更加准确的结果^[9-11]。例如，考虑到无人机部署在基站受损地区等有限区域内的情况，文献[9]利用二项点过程对无人机的位置进行建模，分析了该无人机辅助通信系统下的覆盖率。考虑热点地区的基站呈簇分布特性，文献[10]利用泊松簇过程对无人机的位置进行建模并通过分析得到了最大化系统覆盖率的最优部署高度。考虑到无人机实际部署中存在最小距离限制，文献[11]利用Matern硬核点过程(Matern hardcore point processes, MHP)建模单层无人机网络，并推导分析了安全速率。

上述无人机辅助蜂窝网络系统的相关工作为网络部署设计提供了理论依据，但依然存在不足之处。因而，本文的研究动机有如下两点：1) 虽然文献[11]利用MHP建模了无人机网络，但其研究的是单层网络，双层空地网络模型仍有待进一步的研究。由于MHP的点间排斥特性以及考虑双层空地共信道网络下会额外引入的跨层干扰，总干扰项的拉普拉斯函数的计算将会变得更加复杂。因此为了便于评估系统性能，需要推导更为简洁的系统性能表达式。2)由于无人机空对地(air-to-ground, A2G)信道的视距(line-of-sight, LoS)主导特性，在双层共信道网络中无人机的A2G信道将会不可避免地对地面基站用户造成严重的跨层干扰。采取有效的干扰管理措施可以更好地抑制A2G信道的跨层干扰，保护基站用户速率并提升系统性能，例如主区域保护措施^[7]、功率控制等。综合考虑上述两点，本文形成了一个系统的数学框架，即基于MHP的双层无人机辅助蜂窝网络系统性能分析框架。

本文考虑采用PPP来建模地面基站的位置，利用MHP建模无人机的位置以确保无人机之间的距离满足最小安全限制^[12]。同时利用功率控制来缓解无人机对基站用户造成的干扰。除此之外，由于MHP模型下总干扰的拉普拉斯变换比PPP更为复杂，分析时更加困难，本文基于平均干扰信号比(mean interference-to-signal ratio, MISR)增益法^[13]，首次得到基于MHP建模的空地异构网络的MISR增益值，并利用该增益值将信干比(signal-to-interference ratio, SIR)分布简化近似为PPP模型下的SIR分布。基于上述推导得到的SIR近似分布，获得了更为简洁的用户平均速率近似表达式，并通过蒙特卡洛仿真对该表达式的准确性进行验证，探究了各关键系统参数对空地双层网络性能的影响。结果表明无人机高度和功率控制因子均会对性能造成明显的影响，而且通过优化分析可以发现在本文的框架下功率控制对性能的影响较之高度更为显著。

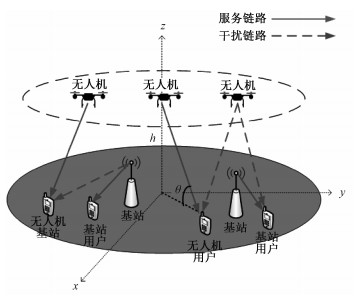
1 系统模型

本文考虑如图 1所示的下行双层异构网络，其中u和b分别表示无人机层和基站层。无人机部署在高度为h的平面内，其位置分布建模为密度为λ_u的MHP点过程Φ_u={x₀^u, x₁^u, x₂^u, …}。地面基站建模为密度为λ_b的PPP点过程Φ_b={x₀^b, x₁^b, x₂^b, …}。无人机的传输功率为P_u，每个无人机服务距其最近的单天线用户，用户服从PPP分布，无人机用户和其对应的服务无人机之间的距离分布为$f_{r_{\mathrm{u}}}(r)=2 \pi \lambda_{\mathrm{u}} r \mathrm{e}^{-\pi \lambda_{\mathrm{u}}\left(r^2-h^2\right)}$。地面基站的发射功率为P_b，每个基站服务一个用户，用户均匀分布在以基站x_i^b为中心，半径为R_b的圆形区域内，基站用户和服务基站之间的距离分布为$f_{r_{\mathrm{b}}}(r)=\frac{2 r}{R_{\mathrm{b}}^2}, 0 \leqslant r \leqslant R_{\mathrm{b}}$^[14]。考虑到频谱资源的稀缺性，假设无人机与基站采取频率复用。为避免频谱复用场景下地面基站受到的来自无人机的强烈干扰，对无人机采用功率控制降低自身传输功率到ηP_u，η∈[0, 1]是功率控制因子。

对于地面基站与地面用户之间的地对地(ground-to-ground, G2G)传输，采用路径损耗指数α_b>2的标准路径损耗模型并假设该信道的小尺度衰落为均值为1的瑞利衰落。无人机到地面用户的A2G信道根据环境的不同，可以是LoS或非视距(non-LoS, NLoS)型信道，信道为LoS的概率表达式^[15]为

$ P_{\mathrm{L}}(r)=\frac{1}{1+C \exp [-B(\theta-C)]}, $

(1)

其中：$\theta=\frac{180}{\pi} \arcsin \left(\frac{h}{r}\right)$，表示的是一个A2G信道的仰角，B, C为常量，与部署环境相关。NLoS信道的概率为P_N(r)=1-P_L(r)。无人机分布的点过程Φ_u根据LoS概率可以分为相互独立的两个集合，属于LoS信道的集合Φ_L={x₀^L, x₁^L, x₂^L, …}与属于NLoS信道的集合Φ_N={x₀^N, x₁^N, x₂^N, …}，路径损耗指数分别为α_L和α_N。小尺度衰落为Nakagami-m衰落模型^[16]，参数为m_L和m_N，服从分布函数为$f_{g_{x_i^{\mathrm{u}}}}(g)=\frac{m^m g^{m-1}}{\Gamma(m)} \mathrm{e}^{-m g}$, ∀x_i^u∈Φ_u，其中$\Gamma(m)=\int\limits_0^{\infty} x^{m-1} \mathrm{e}^{-x} \mathrm{d} x$。考虑到该网络属于典型的干扰受限网络模型，本文忽略噪声影响。

首先定义用户端的SIR，由于MHP与PPP均为静态点过程，考虑位于原点的典型用户进行分析：

1) 典型基站用户接收到的SIR₀^b表达式为

$ \operatorname{SIR}_0^{\mathrm{b}}=\frac{g_{00}^{\mathrm{bb}}\left\|x_0^{\mathrm{b}}\right\|^{-\alpha_{\mathrm{b}}}}{I_{\mathrm{u}}^{\mathrm{b}}+I_{\mathrm{b}}}, $

(2)

其中：I_u^b为接收到的来自无人机的总干扰，I_b为来自除服务基站以外的其他基站的总干扰。

$ I_{\mathrm{u}}^{\mathrm{b}}=\frac{\eta P_{\mathrm{u}}}{P_{\mathrm{b}}}\left(\sum\limits_{x_i^{\mathrm{L}} \in \Phi_{\mathrm{L}}}\left\|x_i^{\mathrm{L}}\right\|^{-\alpha_{\mathrm{L}}} g_{i 0}^{\mathrm{Lb}}+\sum\limits_{x_j^{\mathrm{N}} \in \Phi_{\mathrm{N}}}\left\|x_j^{\mathrm{N}}\right\|^{-\alpha_{\mathrm{N}}} g_{j 0}^{\mathrm{Nb}}\right), $

(3)

$ I_{\mathrm{b}}=\sum\limits_{x_k^{\mathrm{b}} \in \Phi_{\mathrm{b}} \backslash\left\{x_0^{\mathrm{b}}\right\}}\left\|x_k^{\mathrm{b}}\right\|^{-\alpha_{\mathrm{b}}} g_{k 0}^{\mathrm{bb}}. $

(4)

其中：g₀₀^bb, g_k0^bb~exp(1)是典型基站用户到服务基站x₀^b和干扰基站$x_k^{\mathrm{b}} \in \Phi_{\mathrm{b}} \backslash\left\{x_0^{\mathrm{b}}\right\}$的信道之间的信道增益^[17]。g_i0^Lb，g_j0^Nb分别表示典型基站用户到LoS无人机x_i^L∈Φ_L与NLoS无人机x_j^N∈Φ_N之间的信道增益，服从参数分别为m_L和m_N的Gamma分布。

2) 典型无人机用户接收到的SIR₀^s表达式为

$ \operatorname{SIR}_0^s=\frac{g_{00}^{s s}\left\|x_0^s\right\|^{-\alpha_s}}{I_{\mathrm{b}}^s+I_{\mathrm{u}}}, $

(5)

其中：I_b^s是来自所有基站的总干扰，I_u是来自干扰无人机的总干扰和，具体表达式如下

$ I_{\mathrm{u}}=\sum\limits_{x_i^s \in \Phi_s \backslash\left\{x_0^s\right\}}\left\|x_i^s\right\|^{-\alpha_s} g_{i 0}^{s s}+\sum\limits_{x_j^{s^{\prime}} \in \Phi_{s^{\prime}}}\left\|x_j^{s^{\prime}}\right\|^{-\alpha_{s^{\prime}}} g_{j 0}^{s^{\prime} s}, $

(6)

$ I_{\mathrm{b}}^s=\frac{P_{\mathrm{b}}}{\eta P} \sum\limits_{u_{x_k^{\mathrm{b}} \in \Phi_{\mathrm{b}}}}\left\|x_k^{\mathrm{b}}\right\|^{-\alpha_{\mathrm{b}}} g_{k 0}^{\mathrm{b} s}. $

(7)

其中：$s \in\{\mathrm{L}, \mathrm{N}\}, s^{\prime}=\{\mathrm{L}, \mathrm{N}\} \backslash\{s\}$。g_k0^bs~exp(1)是典型无人机用户和地面基站x_k^b∈Φ_b之间的信道增益。g₀₀^ss与g_i0^ss、g_j0^s′s分别是典型无人机用户与它的服务无人机x₀^s和干扰无人机(x_i^s∈Φ_s\{x₀^s}、x_j^s′∈Φ_s′)之间的信道增益，服从参数为m_s的Gamma分布。

系统区域频谱效率(area spectrum efficiency, ASE)定义为单位面积内每赫兹的平均吞吐量

$ \mathrm{ASE}=\lambda_{\mathrm{u}} R_{\mathrm{u}}+\lambda_{\mathrm{b}} R_{\mathrm{B}}. $

(8)

其中：R_u=$\mathbb{E}$[log(1+SIR₀^s)]表示典型无人机用户的平均数据速率，R_B=$\mathbb{E}$[log(1+SIR₀^b)]表示典型基站用户的平均数据速率。

2 Matern硬核点过程

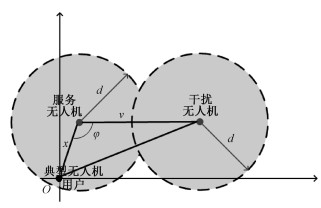
MHP是一种具有排斥特性的点过程，即MHP内部两点之间的距离不能小于某一阈值d，如图 2所示。

MHP是由一个PPP点过程$\Phi_{\mathrm{P}}=\left\{x_0^{\mathrm{P}}, x_1^{\mathrm{P}}, x_2^{\mathrm{P}}, \cdots\right\}$经过稀释得来的^[12]，即MHP密度可表示为

$ \lambda_{\mathrm{u}}=\frac{1-\exp \left(-\lambda_{\mathrm{P}} \pi d^2\right)}{\pi d^2}. $

(9)

对于Φ_P，利用坎贝尔定理可以得到Φ_P中去除位于原点‘O’的服务无人机之外的其他干扰无人机的平均数目表达式

$ \mathbb{E} ^{! o}\left[\sum\limits_{v \in \Phi_{\mathrm{P}}} f(v)\right]=\int_{\mathbb{R}^2} \lambda_{\mathrm{P}} f(v) \mathrm{d} v. $

(10)

而对于MHP点过程Φ_u，其表达式为

$ \mathbb{E}^{! o}\left[\sum\limits_{v \in \Phi_u} f(v)\right]=\lambda_u^{-1} \int_{\mathbb{R}^2} f(v) \chi^{(2)}(v) \mathrm{d} v, $

(11)

$ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\chi^{(2)}(v)= \\ \left\{\begin{array}{l} \frac{2 V(v)\left[1-\mathrm{e}^{-\lambda_{\mathrm{p}} \pi d^2}\right]-2 \pi d^2\left[1-\mathrm{e}^{-\lambda_{\mathrm{p}} V(v)}\right]}{\pi d^2 V(v)\left[V(v)-\pi d^2\right]}, d \leqslant v \leqslant 2 d, \\ \lambda_{\mathrm{u}}{ }^2, v \geqslant 2 d, \\ 0, \text { otherwise. } \end{array}\right. $

(12)

其中：$f(v): \mathbb{R}^2 \rightarrow[0, \infty]$是可测可积函数；χ⁽²⁾(v)为Φ_u的二阶密度积，v为服务无人机与干扰无人机之间的距离。V(v)表示图 2中两圆相交处的面积，其表达式为

$ V(v)=2 \pi d^2-2 d^2 \cos ^{-1}\left(\frac{v}{2 d}\right)+v \sqrt{d^2-\frac{v^2}{4}}. $

(13)

3 MHP下基于MISR的增益值

由上一节可以发现MHP点过程内部的排斥特性使得干扰计算过程变得十分繁琐。为解决这个问题，采用基于MISR的增益方法来将其SIR分布近似转化为PPP的SIR分布^[13]，计算公式为

$ G=\frac{\mathrm{MISR}_{\mathrm{PPP}}}{\mathrm{MISR}}, $

(14)

其中：$\operatorname{MISR} \triangleq \mathbb{E}\left(1 / \mathbb{E}_g(\mathrm{S})\right), \mathbb{E}_g(\mathrm{S})$为衰落过程中的平均信号功率。接下来将在定理1中推导得到MISR_PPP与MISR_MHP。

定理1  MISR_PPP与MISR_MHP表达式如下：

$ \operatorname{MISR}_{\mathrm{PPP}}=\sum\limits_{s \in\{\mathrm{L}, \mathrm{N}\}} \int\limits_h^{\infty} P_s(\mathrm{r}) \mathbb{E}_{\mathrm{P}, s}(\mathrm{I\overline{S}R} \mid r) f_{r_{\mathrm{P}}}(r) \mathrm{d} r . $

(15)

$ \mathrm{MISR}_{\mathrm{MHP}}=\sum\limits_{s \in\{\mathrm{L}, \mathrm{N}\}} \int\limits_h^{\infty} P_s(\mathrm{r}) \mathbb{E}_{\mathrm{u}, s}(\mathrm{I\overline{S}} \mathrm{R} \mid r) f_{r_{\mathrm{u}}}(r) \mathrm{d} r . $

(16)

其中：

$ \mathbb{E}_{\mathrm{P}, s}(\mathrm{I\overline{S}} \mathrm{R} \mid r)=2 \pi \lambda_{\mathrm{P}} r^{\alpha_s} \sum\limits_{q \in\{\mathrm{L}, \mathrm{N}\}} \int_r^{\infty} P_q(y) y^{1-\alpha_q} \mathrm{d} y. $

(17)

$ \mathbb{E}_{\mathrm{u}, s}(\mathrm{IS} \mathrm{R} \mid r)=\frac{r^{\alpha_s}}{\lambda_{\mathrm{u}}} \int\limits_0^{2 \pi}\int\limits_{v_1}^{v_2} F(x, v, \varphi) \chi_1^{(2)}(v) \mathrm{d} v \mathrm{d} \varphi+\\ \frac{r^{\alpha_s}}{\lambda_{\mathrm{u}}} \int\limits_0^{2 \pi}\int\limits_{v_2}^{\infty} F(x, v, \varphi) \chi_2^{(2)}(v) \mathrm{d} v \mathrm{d} \varphi, $

(18)

$ F(x, v, \varphi)=\sum\limits_{q \in\{\mathrm{L}, \mathrm{N}\}} \frac{P_q(v) v}{\left(\sqrt{v^2+r^2-2 x v \cos (\varphi)}\right)^{\alpha_q}} . $

(19)

其中：水平距离$x=\sqrt{r^2-h^2}$，积分上下界v₁=$\max [d, 2 x|\cos (\varphi)|], v_2=\max [2 d, 2 x|\cos (\varphi)|]$。用户距离分布函数为$f_{r_k}(r)=2 \pi \lambda_k r \mathrm{e}^{-\pi \lambda_k\left(r^2-h^2\right)}$，k∈{u, P}。为简化表达式，χ⁽²⁾(v)简化为

$ \chi^{(2)}(v)= \begin{cases}\chi_1^{(2)}(v), & \text { if } d \leqslant v \leqslant 2 d, \\ \chi_2^{(2)}(v), & \text { if } v \geqslant 2 d.\end{cases} $

(20)

证明：见附录定理1的证明。

4 用户平均可达速率分析

利用容量引理^[18]，定理2给出了无人机用户速率$\hat{R}_{\mathrm{u}}$与基站用户速率$\hat{R}_{\mathrm{B}}$的近似表达式。

定理2  $\hat{R}_{\mathrm{u}}$与$\hat{R}_{\mathrm{B}}$的表达式为

$ \hat{{R}}_{\mathrm{u}}=\sum\limits_{s \in\{\mathrm{L}, \mathrm{N}\}} \int\limits_0^{\infty}\int\limits_h^{\infty} \frac{1-\left(1+z / m_s\right)^{-m_s}}{z} P_s(r) \mathrm{e}^{-K_s(r, z)} f_{r_{\mathrm{P}}}(r) \mathrm{d} r \mathrm{d} z, $

(21)

$ \hat{R}_{\mathrm{B}}=\int\limits_0^{\infty}\int\limits_0^{R_{\mathrm{b}}} \frac{1-(z+1)^{-1}}{z} \mathrm{e}^{-K_{\mathrm{b}}(r, z)} \frac{2 r}{R_{\mathrm{b}}^2} \mathrm{d} r \mathrm{d} z, $

(22)

其中，K_s(r, z)与K_b(r, z)具体表达式如下:

$ \begin{aligned} K_{\mathrm{s}}(r, z)=& 2 \pi \lambda_{\mathrm{P}} \int\limits_r^{\infty} \kappa_s(r, y, z) y \mathrm{d} y+\\ & \frac{2 \pi \lambda_{\mathrm{b}}}{\alpha_{\mathrm{b}}}\left(\frac{z P_{\mathrm{b}} r^{\alpha_s}}{\eta P_{\mathrm{u}}}\right)^{\frac{2}{\alpha_{\mathrm{b}}}} B\left(\frac{2}{\alpha_{\mathrm{b}}}, 1-\frac{2}{\alpha_{\mathrm{b}}}\right), \end{aligned} $

(23)

$ \begin{aligned} K_{\mathrm{b}}(r, z)=& 2 \pi \lambda_{\mathrm{u}} \int\limits_h^{\infty} \kappa_{\mathrm{b}}(r, y, z) y \mathrm{d} y+\\ & \frac{2 \pi \lambda_{\mathrm{b}} z^{\frac{2}{\alpha_{\mathrm{b}}}} r^2}{\alpha_{\mathrm{b}}} B\left(\frac{2}{\alpha_{\mathrm{b}}}, 1-\frac{2}{\alpha_{\mathrm{b}}}\right), \end{aligned} $

(24)

上式中，$B(P, Q)=\int\limits_0^1 x^{P-1}(1-x)^{Q-1} \mathrm{d} x$。κ_s(r, y, z) 与κ_b(r, y, z)表达式为:

$ \kappa_s(r, y, z)=\sum\limits_{q \in\{\mathrm{L}, \mathrm{N}\}}\left[1-\left(1+z \frac{y^{-\alpha_q} r^{\alpha_s}}{m_q G}\right)^{-m_q}\right] P_q(y), $

(25)

$ \kappa_{\mathrm{b}}(r, y, z)=\sum\limits_{q \in\{\mathrm{L}, \mathrm{N}\}}\left[1-\left(1+z \frac{\eta P_{\mathrm{u}} r^{\alpha_{\mathrm{b}}}}{P_{\mathrm{b}} m_q y^{\alpha_q}}\right)^{-m_q}\right] P_q(y). $

(26)

证明：见附录定理2的证明。

关于系统ASE表达式，将式(21)和式(22)代入式(8)即可得到，为节省空间不再赘述。

5 仿真结果与分析

本节基于MATLAB仿真检验理论解析式的准确性。考虑仿真环境为密集城市环境，参数如表 1所示。

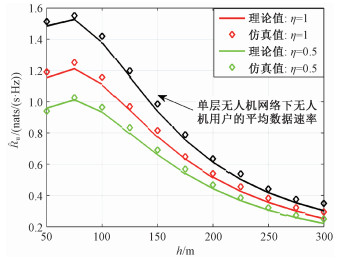
图 3和图 4分别给出了无人机组网场景下无人机用户与基站用户的平均数据速率以及单层无人机网络或单层基站网络下的用户平均数据速率。

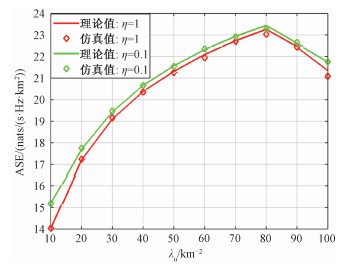
根据仿真结果对比，可以发现理论值结果与仿真结果吻合，验证了基于MISR增益法得到的用户数据速率近似表达式的准确性，在之后的分析中可以利用理论结果代替复杂且耗时的仿真来评估在不同参数下的网络性能并进行下一步的优化配置等。图 5则展示了系统ASE与无人机部署密度之间的关系，可以发现通过部署无人机辅助地面基站可以有效改善系统的整体ASE，而且当无人机的密度过大时，干扰也随着增大，此时互干扰问题带来的影响会大于密集部署带来的增益导致系统ASE开始出现下降趋势。

由上述结果可以看出无人机的部署给地面基站用户带来的跨层干扰使基站用户端的性能变差。通过推导得到的解析表达式结果可以进一步形成一个优化问题，在保证基站用户维持在一定速率以上的前提下，通过调整无人机传输功率与部署高度的大小，最优化无人机用户的速率。通过解优化问题可以得到无人机的最优参数配置，进而在最大化无人机用户平均数据速率的同时实现基站用户与无人机用户二者性能之间的一个平衡。

6 无人机最优配置参数

本节将讨论如何得到无人机用户与基站用户的性能之间平衡的最优参数值。换言之，在约束条件$\hat{R}$_B(η, h)≥R_th下，需要找到最优的(η^*, h^*)来最大化$\hat{R}$_u(η, h)，其中R_th是基站用户平均数据速率的阈值，形成优化问题如下

$ \begin{aligned} &\mathrm{P}_0: \max _{h ; \eta \in[0, 1]} \hat{R}_{\mathrm{u}}(\eta, h) \\ &\quad \text { s.t. } \hat{R}_{\mathrm{B}}(\eta, h) \geqslant R_{\mathrm{th}}. \end{aligned} $

(27)

基于莱布尼茨积分法则，可以证明$\hat{R}$_u(η, h)随η单调递增，而$\hat{R}$_B(η, h)随η单调递减。通过反证法可以发现P₀的约束可以用$\hat{R}$_B(η, h)=R_th来代替。首先，以一定的精度遍历[50, 300]范围内所有的h。然后根据用户速率对η的单调性，通过二分查找求出满足$\hat{R}$_B(η, h)=R_th情况下所有(η, h)组合。最后，选择令$\hat{R}$_u(η, h)最大化的(η^*, h^*)作为最优参数组合，结果如表 2所示。

由于无人机需要牺牲自身用户性能来保证基站用户的性能，由表 2可以观察到$\hat{R}$_u随着R_th单调递减。除此之外，注意到除了R_th=0.6这一特殊情况，η^*随着R_th的增加而减少但是h^*总是50 m，这是因为无人机用户平均数据速率存在一个最优高度，可以通过更低的功率控制因子来得到更高的$\hat{R}$_u^*。η^*总体趋势是在不断降低，这是因为在h^*维持不变的前提下，为了满足更高的R_th，无人机需要通过不断降低η^*来降低自己的传输功率从而减少对基站用户的跨层干扰。通过上述结果，明显可以发现相较于调整无人机的部署高度，调整无人机的传输功率对系统性能的影响更为显著。

7 结束语

本文研究双层无人机辅助蜂窝网络系统下的统计性能，首次得到MHP模型下的MISR增益值，并推导得到更简洁的用户平均数据速率近似表达式，最后通过仿真验证了表达式的准确性。仿真结果展示了系统关键部署参数对平均用户数据速率的影响。此外，针对无人机部署高度与功率控制因子对用户数据速率的影响，讨论了两种参数的最优组合，优化结果表明功率控制因子对性能的影响相比高度更为显著。目前本文仅考虑了下行无人机辅助通信网络下用户数据速率进行推导分析，未来可以将本文的工作扩展到上行链路中，关注基站端接收到来自用户的信号干扰比分布以及各系统参数对性能指标的影响。

附录

定理1的证明

PPP和MHP模型下无人机层$\mathbb{E}$_{P, s}(ISR|r)和$\mathbb{E}$_{u, s}(ISR|r)(s∈{L, N})的计算式如下。对于PPP点过程Φ_P={x₀^P, x₁^P, x₂^P, …}，可根据概率LoS模型将其分为两个相互独立的集合，Φ_P=Φ_{P, L}∪Φ_{P, N}，其中Φ_{P, L}={x₀^{P, L}, x₁^{P, L}, x₂^{P, L}, …}，Φ_{P, N}={x₀^{P, N}, x₁^{P, N}, x₂^{P, N}, …}。为简化表示，假设服务信道距离为r，干扰信道距离为y，首先考虑服务A2G信道为LoS型的情况：

$ \mathbb{E}_{\mathrm{P}, \mathrm{L}}(\mathrm{I\overline{S}R} \mid r)=\left[\sum\limits_{x_i^{\mathrm{P}, \mathrm{L}} \in \Phi_{\mathrm{P}, \mathrm{L}} \backslash\left\{x_0^{\mathrm{P}, \mathrm{L}}\right\}} \frac{\left\|x_0^{\mathrm{P}, \mathrm{L}}\right\|^{\alpha_{\mathrm{L}}}}{\left\|x_i^{\mathrm{P}, \mathrm{L}}\right\|^{\alpha_{\mathrm{L}}}}+\sum\limits_{x_j^{\mathrm{P}, \mathrm{N}} \in \Phi_{\mathrm{P}, \mathrm{N}}} \frac{\left\|x_0^{\mathrm{P}, \mathrm{L}}\right\|^{\alpha_{\mathrm{L}}}}{\left\|x_j^{\mathrm{P}, \mathrm{N}}\right\|^{\alpha_{\mathrm{N}}}}\right]\stackrel{(\mathrm{a})}{=} \sum\limits_{q \in\{\mathrm{L}, \mathrm{N}\}} 2 \pi \lambda_{\mathrm{P}} r^{\alpha_{\mathrm{L}}} \int\limits_r^{\infty} P_q(y) y^{1-\alpha_q} \mathrm{d} y, $

(A1)

$ \mathbb{E}_{\mathrm{u}, \mathrm{L}}(\mathrm{I\overline{S}} \mathrm{R} \mid r)==\sum\limits_{x_i^{\mathrm{L}} \in \Phi_{\mathrm{L}} \backslash\left\{x_0^{\mathrm{L}}\right\}}\left(\frac{\left\|x_0^{\mathrm{L}}\right\|}{\left\|x_i^{\mathrm{L}}\right\|}\right)^{\alpha_{\mathrm{L}}}+\sum\limits_{x_j^{\mathrm{N}} \in \Phi_{\mathrm{N}}} \frac{\left\|x_0^{\mathrm{L}}\right\|^{\alpha_{\mathrm{L}}}}{\left\|x_j^{\mathrm{N}}\right\|^{\alpha_{\mathrm{N}}}}\\ \stackrel{\text { (b) }}{=} \frac{r^{\alpha_{\mathrm{L}}}}{\lambda_{\mathrm{u}}} \left[ {\int\limits_0^{2 \pi}\int\limits_{v_1}^{v_2} \sum\limits_{q \in\{\mathrm{L}, \mathrm{N}\}}\frac{P_q(v) \chi_1^{(2)}(v) v}{\left(\sqrt{v^2+\mathrm{r}^2-2 x v \cos (\varphi)}\right)^{\alpha_q}} \mathrm{d} \varphi \mathrm{d} v+\int\limits_0^{2 \pi}\int\limits_{v_2}^{\infty}\sum\limits_{q \in\{\mathrm{L}, \mathrm{N}\}} \frac{P_q(v) \chi_2^{(2)}(v) v}{\left(\sqrt{v^2+\mathrm{r}^2-2 x v \cos (\varphi)}\right)^{\alpha_q}} \mathrm{d} v \mathrm{d} \varphi} \right]. $

(A2)

其中：(a)、(b)服从坎贝尔定理。当服务信道为NLoS信道时的$\mathbb{E}$_{P, N}(ISR|r)，$\mathbb{E}$_{u, N}(ISR|r)的表达式可以通过将式(28)和式(29)中的r^α_L替换成r^α_N得到。

定理2的证明

利用容量计算引理^[18]，可以推导用户平均数据率的表达式

$ \mathbb{E}\left[\log \left(1+\frac{\mathrm{X}}{\mathrm{Y}}\right)\right]=\int\limits_0^{\infty} \frac{1}{z} \mathbb{E}\left[\mathrm{e}^{-z \mathrm{Y}}\right]\left(1-\mathbb{E}\left[\mathrm{e}^{-z \mathrm{X}}\right]\right) \mathrm{d} z. $

(A3)

利用MISR增益值缩放阈值z，可以将非PPP网络的SIR分布精确地近似为PPP网络的SIR分布：

$ \begin{aligned} \mathbb{P}\left(\mathrm{SIR}_0^s>z\right) &=\mathbb{P}\left(g_{00}^{s s}>z\left\|x_0^{\mathrm{P}, s}\right\|^{\alpha_s}\left(I_{\mathrm{b}}^s+I_{\mathrm{u}}\right)\right) \\ & \approx \mathbb{P}\left(g_{00}^{s s}>z\left\|x_0^{\mathrm{P}, s}\right\|^{\alpha_s}\left(I_{\mathrm{b}}^s+I_{\mathrm{u}}^{\mathrm{PPP}} / G\right)\right), \end{aligned} $

(A4)

$ I_{\mathrm{u}}^{\mathrm{PPP}}=\sum\limits_{x_i^{\mathrm{P}, \mathrm{s}} \in \Phi_{\mathrm{P}, s} \backslash\left\{x_0^s\right\}}\left\|x_i^{\mathrm{P}, s}\right\|^{-\alpha_s} g_{i 0}^{s s}+\sum\limits_{x_j^{\mathrm{P}, s^{\prime}} \in \Phi_{\mathrm{P}, s^{\prime}}}\left\|x_j^{\mathrm{P}, s^{\prime}}\right\|^{-\alpha_{s^{\prime}}} g_{j 0}^{s^{\prime} s}. $

(A5)

基于得到的SIR近似分布关系，利用SIR分布与容量的关系$\hat{R}_{\mathrm{u}}=\sum_{s \in\{\mathrm{L}, \mathrm{N}\}} \int\limits_0^{\infty} \frac{\mathbb{P}\left(\mathrm{SIR}_0^s>z\right)}{1+z} \mathrm{d} z$，可以得到无人机用户的近似平均数据速率：

$ \hat{R}_{\mathrm{u}}=\sum\limits_{s \in\{\mathrm{L}, \mathrm{N}\}} \int\limits_0^{\infty} \int\limits_h^{\infty} \frac{1-\mathbb{E}\left[\mathrm{e}^{-z g_{00}^{s s}}\right]}{z} \mathcal{L}_{I, s}(z) f_{r_{\mathrm{P}}}(r) \mathrm{d} z . $

(A6)

其中：$\mathbb{E} \left[\mathrm{e}^{-z g_{00}^{s s}}\right]=\left(z / m_s+1\right)^{-m_s}$，典型用户与服务无人机之间的信道增益g₀₀^ss服从参数为m_s的Nakagami-m衰落模型。干扰项$\mathcal{L}_{I, s}(z)=\mathbb{E}\left[\mathrm{e}^{-z\left\|x_0^{\mathrm{P}, s}\right\|^{\alpha_s}\left(I_{\mathrm{b}}^{\mathrm{s}}+\mathrm{P}_{\mathrm{u}}^{\mathrm{PPP}} / G\right)}\right]$，假设无人机服务信道为LoS型，$\mathcal{L}_{I, \mathrm{L}}(z)$的展开式如下

$ \mathcal{L}_{I, \mathrm{L}}(z)=\underset{x_i^{\mathrm{P}, \mathrm{L}} \in \Phi_{\mathrm{P}, \mathrm{L}} \backslash\left\{x_0^{\mathrm{P}, \mathrm{L}}\right\}}{\mathbb{E}}[ {\text{e}^{-\frac{\left\|x_0^{\mathrm{P}, \mathrm{L}}\right\|{ }^\alpha \mathrm{L}_{g_{i 0}^{\mathrm{LL}}}}{\left\|x_i^{\mathrm{P}, \mathrm{L}}\right\|^{{ }^\alpha \mathrm{L}_G}}}} ] \times \underset{x_j^{\mathrm{P}, \mathrm{N}} \in \Phi_{\mathrm{P}, \mathrm{N}}}{\mathbb{\mathbb { E }}} [\text{e}^{-\frac{\left\|x_0^{\mathrm{P}, \mathrm{L}}\right\|^\alpha \mathrm{L}_{g_{j 0}^{\mathrm{NL}}}}{\| x_j^{\mathrm{P}, \mathrm{N}}{\|}^\alpha N_G}}] \times \underset{x_k^{\mathrm{b}} \in \Phi_{\mathrm{b}}}{\mathbb{\mathbb { E }}}[\text{e}^{-\frac{P_{\mathrm{b}}\left\|x_0^{\mathrm{P}, \mathrm{L}}\right\|^{\alpha_{ \mathrm{L}_{g_{k0}}\mathrm{bL}}}}{\eta P_{\mathrm{u}}\left\|x_k^{\mathrm{b}}\right\|^{\alpha_{\mathrm{b}}}}}] \\ \stackrel{\text { (c) }}{=} \exp \left\{-2 \pi \lambda_P \int\limits_r^{\infty} \sum\limits_{q \in\{\mathrm{L}, \mathrm{N}\}}\left[1-\left(1+z \frac{y^{-\alpha_q} r^{\alpha_{\mathrm{L}}}}{m_q G}\right)^{-m_q}\right] P_q(y) y \mathrm{d} y\right\}\times \exp \left\{-\frac{2 \pi \lambda_{\mathrm{b}}}{\alpha_{\mathrm{b}}}\left(\frac{z P_{\mathrm{b}} r^{\alpha_{\mathrm{L}}}}{\eta P_{\mathrm{u}}}\right)^{\frac{2}{\alpha_{\mathrm{b}}}} B\left(\frac{2}{\alpha_{\mathrm{b}}}, 1-\frac{2}{\alpha_{\mathrm{b}}}\right)\right\}. $

(A7)

其中：(c)为总干扰的概率生成泛函。g_k0^bL~exp(1)，g_i0^LL, g_j0^NL服从参数为m_L与m_N的Nakagami-m衰落。将(34)中的r^α_L替换为r^α_N可得到$\mathcal{L}_{I, \mathrm{N}}(z)$。

基站用户的近似平均数据速率为

$ \hat{R}_{\mathrm{B}}=\int\limits_0^{\infty} \int\limits_0^{R_{\mathrm{b}}} \frac{1-\mathbb{E}\left[\mathrm{e}^{-z g_{00}^{\mathrm{bb}}}\right]}{z} \mathcal{L}_{I, \mathrm{b}}(z) f_{r_{\mathrm{b}}}(r) \mathrm{d} r \mathrm{d} z. $

(A8)

其中：$\mathbb{E}\left[\mathrm{e}^{-z g_{00}^{\mathrm{bb}}}\right]=(z+1)^{-1}$，g₀₀^bb服从瑞利衰落。$\mathcal{L}_{I, \mathrm{b}}(z)=\mathbb{E}\left[\mathrm{e}^{-z\left\|x_0^{\mathrm{b}}\right\|^{-\alpha_{\mathrm{b}}}\left(I_{\mathrm{u}}^{\mathrm{b}}+I_{\mathrm{b}}\right)}\right]$的展开式为

$ \mathcal{L}_{I, \mathrm{b}}(z)=\underset{x_i^{\mathrm{L}} \in \Phi_{\mathrm{L}}}{\mathbb{\mathbb { E }}}[\text{e}^{-\frac{\eta P_{\mathrm{u}}\left\|x_0^{\mathrm{b}}\right\|^\alpha \mathrm{b}}{P_{\mathrm{b}}\left\|x_i^{\mathrm{L}}\right\|^\alpha \mathrm{L}} g_{i 0}^{\mathrm{Lb}}}] \times \underset{x_j^N \in \Phi_\text{N}}{\mathbb{E}}[\text{e}^{-\frac{\eta P_{\mathrm{u}}\left\|x_0^{\mathrm{b}}\right\|^\alpha \mathrm{b}}{P_{\mathrm{b}}\left\|x_j^{\mathrm{N}}\right\|^{\alpha _{\mathrm{N}}}} g_{j 0}^{\mathrm{Nb}}}] \times \underset{x_k^{\mathrm{b}} \in \Phi_{\mathrm{b}} \backslash\left\{x_0^{\mathrm{b}}\right\}}{\mathbb{E}}[\text{e}^{-\frac{\left\|x_0^{\mathrm{b}}\right\|^{\alpha_{\mathrm{b}}}}{\left\|x_k^{\mathrm{b}}\right\|^{\alpha_{\mathrm{b}}}} g_{k 0}^{\mathrm{bb}}}] \\ =\exp \left\{-2 \pi \lambda_{\mathrm{u}} \int\limits_h^{\infty} \sum\limits_{q \in\{\mathrm{L}, \mathrm{N}\}}\left[1-\left(1+z \frac{\eta P_{\mathrm{u}} r^{\alpha_{\mathrm{b}}}}{m_q P_{\mathrm{b}} y^{\alpha_q}}\right)^{-m_q}\right] P_q(y) y \mathrm{d} y\right\}\times \exp \left[-\frac{2 \pi \lambda_{\mathrm{b}}}{\alpha_{\mathrm{b}}} z^{\frac{2}{\alpha_{\mathrm{b}}}} r^2 B\left(\frac{2}{\alpha_{\mathrm{b}}}, 1-\frac{2}{\alpha_{\mathrm{b}}}\right)\right]. $

(A9)