2. 中国科学院大学,北京 100049;
3. 中科卫星应用德清研究院,浙江 德清 313200;
4. 国家卫星气象中心,北京 100081;
5. 北京大学地球与空间科学学院,北京 100871
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Deqing Academy of Satellite Applications, Deqing 313200, Zhejiang, China;
4. National Satellite Meteorological Center, Beijing 100081, China;
5. School of Earth and Space Sciences, Peking University, Beijing 100871, China
自由式滑雪空中技巧作为一项难度系数和危险系数都较高的冬季运动,要求运动员沿赛道下滑一段距离后到达起跳台处,起跳腾空完成指定动作后落地[1]。运动员在滑行加速阶段,主要受重力、支持力、摩擦阻力、风阻力的作用,当运动员到达起跳台处时,出台速度可分解为水平向前和垂直向上2个分量,垂直向上分量决定跳跃高度和滞空时间,向前分量决定前行距离。在整个过程中,赛道环境风会对运动员产生顺风向推力、逆风向阻力以及侧向的偏航力,从而影响运动员完成动作的稳定性以及后续的着陆过程。
现阶段,人们对该项运动赛道风场的认识十分匮乏,仅凭赛道旁的测风标对风场的变化进行模糊的判断。同时,赛道风具有稳定性差和波动强烈的显著特点。因此,对赛道上的风速风向进行定量化研究有着十分重要的意义。本文旨在实现对赛道上超短期内风速风向的变化进行准确预测,以此为这项运动提供实用有效的预报信息,帮助运动员在训练的过程中对风速风向状况作出判断,做好心理准备和姿态调整以应对风速风向的突变,通过不断的训练进一步提升运动员对风速风向变化的适应能力,为运动员稳定性控制与技术训练提供辅助支持作用。
目前,国内外对于风速预测的研究多应用于风电场风速预测[2-6]、结构设计防风风速预测、天气预报风速预测这些领域,对于赛道这种百米尺度的特殊应用场景很少。风速预测按时间尺度可分为长期、中期、短期及超短期风速预测。现有的超短期风速预测主要是对未来几分钟到几个小时尺度的预测,而针对滑雪赛道这一特殊背景的应用需求,本文主要研究时长在10 s到几十秒级别的超短期风速预测。
目前风速预测模型按照其原理大致可分为3类:物理模型、统计模型、混合模型。物理模型以数值天气预报(numerical weather prediction,NWP)为基础,具有计算复杂、预测时长较长(小时级至天级)、适用于大范围预测(预测格网通常在5~25 km)等特点[7],不适用于小范围、超短期的风速预测。而基于历史数据的统计模型法不关注风速涉及的具体物理过程,具有建模简洁、计算速度快、预测准确等优点[8-11]。传统的统计模型包括时间序列分析法中的自回归模型(autoregressive model,AR)、移动平均模型(moving average model,MA)、自回归移动平均模型(autoregressive moving average model,ARMA)、差分自回归移动平均模型(autoregressive integrated moving average model,ARIMA)。随着机器学习的兴起又出现了人工神经网络(artificial neural network, ANN)、支持向量机(support vector machine, SVM)等方法[12-14]。为克服单一模型的局限性,常见的混合模型主要有以下几种思路:第1类是使用优化算法对单一模型进行改进,如刘爱国等[15]利用遗传算法对SVM参数组合进行优化,提高了预测精度;第2类引入卡尔曼滤波、具有时频域分析功能的小波变换及经验模态分解(empirical mode decomposition,EMD)等对数据进行预处理和分解[16-18],对各分量分别进行建模再重构得到最终预测结果,如颜宏文和卢格宇[19]用完备总体经验模态分解(complete ensemble empirical mode decomposition, CEEMD)算法和小波算法进行两次去噪以提高模型预测性能;第3类以近几年发展起来的空间相关法为基础,利用风速上下游之间的相关关系及延迟性进行混合预测[20-22]。
对于体育项目而言,在获取准确的风速预测值的同时,及时捕捉到风速突变的发生也同样重要。本文以某自由式滑雪空中技巧赛道为研究区,前期进行了大量仿真测试实验淘汰了单一模型方法、部分组合方法及空间相关法,这些方法在赛道应用场景上存在预测精度不高及赛道风速风向数据条件不适用的情况。通过对比研究发现,采用小波分析进行组合预测能很好地适用赛道应用场景,改善预测滞后性,实现赛道风速风向的准确预测。综合考虑,本文利用离散小波变换对原始风速风向序列进行分解与重构提取特征分量,再依据各分量特点选择不同模型进行组合预测,得到最终的预测结果。最后对预测结果进一步分析,将其转换为表征赛道风稳定性的指标,并对模型时效性进行分析,以此来验证其实际应用价值及可能性。
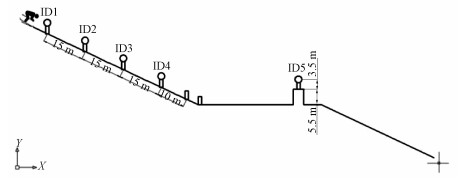
1 数据源 1.1 赛道风速仪布设及数据采集本研究选取某一自由式滑雪空中技巧训练赛道为研究区域,利用超声风速仪进行现场实测,赛道总长度约100 m,助滑区约70 m,在不影响运动员正常训练的前提下,选择沿着赛道一侧安装超声风速仪。本研究主要采集赛道的助滑区域及起跳台处的风速风向数据,考虑到场地的实际大小、铺设电缆的难易程度、赛道上应关注的几个关键位置等因素,最终选定在助滑区域布设4个风速仪、起跳台处布设1个风速仪的实验方案。风速仪依次命名为ID1、ID2、ID3、ID4、ID5(ID5为起跳台处),每秒监测并记录赛道不同位置处的风速风向变化。风速仪布设方式如图 1所示。所用风速仪为WS500-UMB超声风速仪,数据每秒更新一次,风速测量范围为0~75 m/s,观测精度为当风速大于1 m/s时,风速测量精度优于±0.3 m/s;风向测量范围为0°~359.9°,观测均方根误差小于3°。对于本研究,该风速仪可完全满足应用需求。
|
Download:
|
| 图 1 超声风速仪布设图 Fig. 1 Layout of ultrasonic anemometer | |
图 2展示了赛道上5个风速仪所在位置在一段时间内的风速变化情况,观察不同时刻的赛道风速变化情况,可以看出不同位置的风速序列都具有稳定性差,波动剧烈的特点。对于ID1至ID4风速仪,其之间的相关性更高,由于ID5风速仪为运动员起跳位置,其稳定性更差、风速波动更为剧烈。

|
Download:
|
| 图 2 赛道不同位置风速变化图 Fig. 2 Wind speed changes at different positions on the track | |
选取赛道上助滑区和起跳台两个位置处的样本数据对本文采用的组合模型进行仿真实验,对原始采集到的秒级数据每10 s求取平均值进行重采样。第1组样本为1月18日9:30到11:10的ID5处风速风向数据,取前500个采样点数据(5 000 s)训练模型,后100个采样点数据(1 000 s)测试模型。第2组样本为2月9日11:00到16:00的ID3处的风速风向数据,取前1 700个采样点数据(17 000 s)训练模型,后100个采样点数据(1 000 s)测试模型。
2 赛道风速风向预测方法 2.1 小波分解提取特征分量原始赛道风速风向序列具有很强的随机性、波动剧烈的特点,直接使用单一模型进行预测无法取得很好的预测效果。因此,为了提高预测精度,本文利用小波变换对原始序列进行预处理。小波变换能对信号进行多尺度、多分辨率分析,采用离散小波变换的Mallat塔式算法对原始风速风向序列进行多尺度的小波分解以提取原始序列的各特征分量,小波分解每一级分解的结果是将上次分解得到的低频信号再分解成低频和高频两部分,以此实现信号的逐级分解,得到不同尺度下的近似系数和细节系数。
若信号f(t)的连续小波变换表示为
| $ W_{\psi} f(a, b)=\frac{1}{\sqrt{|a|}} \int\limits_{-\infty}^{+\infty} f(t) \hat{\psi}\left(\frac{t-b}{a}\right) \mathrm{d} t. $ | (1) |
其中:
| $ W_{\psi} f(j, k)=a^{-\frac{j}{2}} \int\limits_{-\infty}^{+\infty} f(t) \hat{\psi}\left(a_{0}^{-j} t-k b_{0}\right) \mathrm{d} t. $ | (2) |
用离散小波分解提取原始风速风向序列高低频分量的核心问题是确定最合适的小波函数和分解层数。dbN小波具有良好的紧支撑性和正则性,经过多次实验对比最终选定db10小波对原始风速序列进行离散小波变换。小波分解层数的选取没有明确的理论依据,随着分解的层数增多,信号的频率划分越细,但是在分解过程中会产生计算误差和信息流失,导致精度下降[23]。因此,对于不同的应用场景要根据具体问题具体分析,本文通过实验对比的方式发现在对原始序列分解3层时就能达到理想的预测效果。综合考虑,本文决定采用db10小波进行3次分解与重构。以第1组样本风速序列为例,图 3给出了原始风速序列、分解重构后的低频近似分量a3和高频细节分量d3、d2、d1的波形图。

|
Download:
|
| 图 3 风速序列的db10小波3层分解 Fig. 3 Three-layer decomposition of db10 wavelet | |
观察图 3中原始风速序列及各分量的时序图,可以看出低频分量a3主要反映原始风速序列的趋势,而高频分量d3、d2、d1主要包含原始风速序列的细节及噪声信息。考虑到各频率成分之间的差异性,本文依据各频率成分特点选择不同的模型进行预测,同时组合模型也可以避免单一模型产生的局限性。参考文献[24]采用时间序列的Hurst参数估计方法对各分量的特征进行分析和判断[24],Hurst指数反映时间序列的长程相关性,当H=0.5时,表明该序列是随机性的,无相互依赖;当0.5 < H < 1时,表明该序列具有持续性即长程相关性,H值越接近1,说明持续性越强;当0 < H < 0.5时,表明该序列具有反持续性[25-26]。采用重标度极差分析(rescaled range analysis method, R/S)法对原始风速序列及各分量进行Hurst参数估计,计算结果如表 1所示。
|
|
表 1 原始风速序列及各分量Hurst参数分析结果 Table 1 Hurst parameter analysis results of original wind speed sequence and each component |
根据表 1中各分量Hurst参数分析结果并结合图 3中各分量时序图的特征可知,低频分量a3呈现出一种长程相关性同时具有显著的非线性的特点,反映了原始风速序列的长期趋势,因此对低频分量a3选择采用解决非线性能力更强的NAR动态神经网络进行建模预测。高频分量d3、d2、d1的Hurst参数小于0.5,表现出一种比纯随机序列更强的随机波动,同时时序图也反映了高频分量的非平稳特性,因此对高频分量选择采用对非平稳序列及序列波动部分能较好预测的ARIMA模型来建模预测。
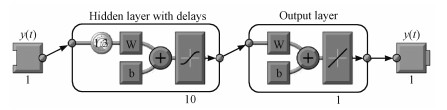
2.2 NAR动态神经网络模型非线性自回归(nonlinear auto regressive,NAR)神经网络是一种有时延输入的神经网络,具有反馈和记忆功能。具有比静态神经网络稳定性更好、解决非线性能力更强、泛化性能更好,且在时序数据预测上保留了较大的关联性的特点[27-28],因此对于分解后得到的低频分量a3进行NAR神经网络建模。网络结构主要由输入层、隐藏层与输入延时层、输出层构成,如图 4。
|
Download:
|
| 图 4 NAR神经网络结构图 Fig. 4 NAR neural network structure diagram | |
图 4中左侧的y(t)表示网络输入,右侧的y(t)表示网络输出,1∶3表示延迟阶数,W表示联结权值,b表示阈值。NAR神经网络模型可以表示为
| $ y(t)=f(y(t-1), y(t-2), \cdots, y(t-d)) . $ | (3) |
式中: d为输入延迟阶数。可以看出y(t)的未来值由该序列过去的d个历史值所决定,在本研究中即风速序列的下一时刻值v(t)是由过去d个历史值v(t-1),v(t-2),…,v(t-d)预测得到。
使用NAR神经网络训练样本数据时,首先将样本数据进行划分,设置训练集、验证集和测试集的比例。本研究选取训练数据的70%作为训练集,用于网络训练,15%作为验证集,验证网络归一化程度,防止网络过拟合,15%作为测试集,用于对预测性能进行测试。其次设置网络的延迟阶数和隐藏层神经元个数,这两者是网络拓扑结构的关键参数,关系到函数关系能否被网络准确学习。但是延时阶数、隐层神经元个数选取没有成熟的理论依据,只能由经验给出,因此需要反复调试。通过不断调试,确定最优延迟阶数为3,隐藏层神经元个数为10。最后,为避免网络出现过拟合的问题,模型的训练算法选择贝叶斯正则化算法(Bayesian regularization)提升网络的泛化能力[29],同时传递函数设定为tansig函数,权值自适应学习函数设定为learngd函数,性能函数采用MSE。通过误差自相关曲线以及目标值与输出值误差图判断拟合效果[30],当训练数据自相关误差在上下置信区间内,且拟合误差在目标误差0.005以下时,可以停止训练并保存训练好的神经网络的各项参数,开始进行预测。
2.3 ARIMA模型对于各高频分量选择建立差分自回归移动平均模型(autoregressive integrated moving average model,ARIMA)。预测的步骤主要包括:1)数据平稳化处理;2)模型识别;3)模型定阶;4)模型参数估计;5)模型适应性检验;6)模型预测。
首先利用单位根检验判断各高频分量是否平稳,对非平稳序列进行一阶差分处理转换为平稳序列,由自相关系数图和偏自相关系数图的截尾性初步确定模型类别,并通过AIC准则(赤池信息准则)确定模型阶数,模型的一般表达式为
| $ \begin{gathered} X_{t}-\varphi_{1} X_{t-1}-\varphi_{2} X_{t-2}-\cdots-\varphi_{p} X_{t-p}= \\ \varepsilon_{t}-\theta_{1} \varepsilon_{t-1}-\theta_{2} \varepsilon_{t-2}-\cdots-\theta_{q} \varepsilon_{t-q} \cdot \end{gathered} $ | (4) |
式中: p和q是模型的自回归阶数和移动平均阶数;ϕ,θ是不为零的待定系数;εt是独立的误差项。
经过上述步骤最终确定高频分量d3、d2、d1的模型依次为ARIMA(6, 1, 5),ARIMA(5, 1, 5),ARIMA(5, 1, 4),且模型能通过白噪声检验。
2.4 DWT-NAR-ARIMA组合预测模型本文采用的DWT-NAR-ARIMA组合模型预测方法可表示成图 5,具体预测流程主要包括3个步骤:1)在确定合适的小波函数和分解层数后,利用小波分解重构算法对输入序列进行分解,得到原始序列的低频近似分量和高频细节分量;2)对低频分量建立NAR神经网络模型,选取合适的延迟阶数和隐藏层神经元个数进行训练和预测。3)各高频分量进行平稳化处理,再通过模型识别、定阶和参数估计建立ARIMA模型进行预测。最后将各分量预测结果经过组合相加即可得到最终的预测结果。

|
Download:
|
| 图 5 DWT-NAR-ARIMA模型预测流程 Fig. 5 DWT-NAR-ARIMA model prediction process | |
对低频分量a3选取NAR模型的输入延迟阶数为3,样本数据的前500个值(V1~V500)用于训练模型,后100个值(V501~V600)用于测试模型,模型训练过程为:训练集由实测值V1~V3得到预测值V4,由实测值V2~V4得到预测值V5,以此类推,直到由实测值V497~V499得到预测值V500,通过训练得到符合条件的模型。在模型完成训练后,把测试集数据代入预测模型,由实测值V498~V500得到预测值V501,随时间向前一步代入新的实测值,由实测值V499~V501得到预测值V502,以此类推,直到由实测值V597~V599得到预测值V600即完成了测试样本100个值的超前一步滚动预测。
对于高频分量d3、d2、d1分别建立ARIMA模型,同样选取样本数据的前500个值(V1~V500)用于训练模型,后100个值(V501~V600)用于测试模型。在利用训练集对模型完成定阶、参数识别、适应性检验后,把测试集数据代入模型,由实测值V1~V500得到预测值V501,随时间向前一步代入新的实测值,由实测值V1~V501得到预测值V502,以此类推,直到由实测值V1~V599得到预测值V600即完成了测试样本100个值的超前一步滚动预测。
在分别完成各分量测试样本的滚动预测后,将4个分量的预测结果进行组合相加即可得到原始风速序列的最终预测值。第1组样本的风向预测流程和第2组样本风速风向预测的流程同上。
3 预测结果及误差分析本文采用平均绝对误差(mean absolute error,MAE)、平均绝对百分误差(mean absolute percent error,MAPE)、均方根误差(root mean square error,RMSE)评价模型预测精度,同时为反映模型预测风速风向突变的能力,引入欧几里得距离和Pearson相关系数作为新的评价指标,通过计算预测序列与真实序列之间的距离和相似度来评价模型是否能准确地预测到风速风向突变的发生。
5个评价指标的计算公式如下:
| $ e_{\mathrm{MAE}}=\frac{1}{n} \sum\limits_{t=1}^{n}|v(t)-\hat{v}(t)|. $ | (5) |
| $ e_{\mathrm{MAPE}}=\frac{1}{n} \sum\limits_{t=1}^{n}\left|\frac{v(t)-\hat{v}(t)}{v(t)} \times 100\right|. $ | (6) |
| $ e_{\mathrm{RMSE}}=\sqrt{\frac{1}{n} \sum\limits_{t=1}^{n}(v(t)-\hat{v}(t))^{2}}. $ | (7) |
| $ \operatorname{dist}(X, Y)=\sqrt{\sum\limits_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}}. $ | (8) |
| $ \rho_{X, Y}=\frac{N \sum X Y-\sum X \sum Y}{\sqrt{N \sum X^{2}-\left(\sum X\right)^{2}} \sqrt{N \sum Y^{2}-\left(\sum Y\right)^{2}}}. $ | (9) |
式(5)到式(7)中v(t)表示实际风速,
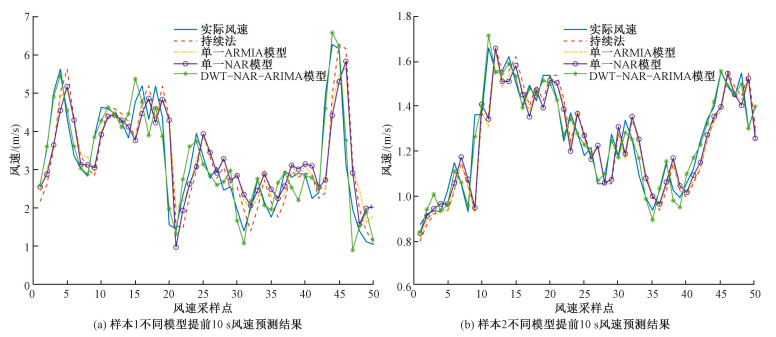
使用持续法、单一ARIMA模型、单一NAR模型对两组样本同样进行超前一步预测,并与本文使用的组合预测模型进行对比。图 6展示了两组样本不同模型的风速预测结果(为展示清晰,仅截取前50个结果),可以看出单一模型预测结果具有明显的滞后性,本文使用的DWT-NAR-ARIMA组合模型能有效地改善这一滞后性,预测序列的波峰与波谷出现的时间点基本与真实序列重合,这也表明组合模型对于风速突变点的预测更为准确。从表 2可以看出DWT-NAR-ARIMA组合模型各项指标均优于单一预测模型,与单一模型预测误差最低方法相比,样本1和样本2的MAPE分别减少63.55%、62.14%,RMSE分别减少63.53%、66.67%。从不同模型欧几里得距离和Pearson相关系数的对比也可以看出运用组合模型预测的结果与原始风速序列更为贴近,序列间的相似度更高。对于体育项目而言,不仅需要获取准确的风速预测值,预测风速突变的发生也同样重要,本文使用的DWT-NAR-ARIMA组合模型在这两点上显然优于任意一种单一模型。而样本2(平均风速1.219 4 m/s)相较于样本1(平均风速4.053 5 m/s)的整体风速值偏小,风速波动较平缓,因此对于样本2整体的预测精度更高。
|
Download:
|
| 图 6 两组样本不同模型风速预测结果 Fig. 6 Wind speed prediction results of two samples with different models | |
|
|
表 2 两组样本不同模型风速预测误差 Table 2 Wind speed prediction errors of two samples with different models |
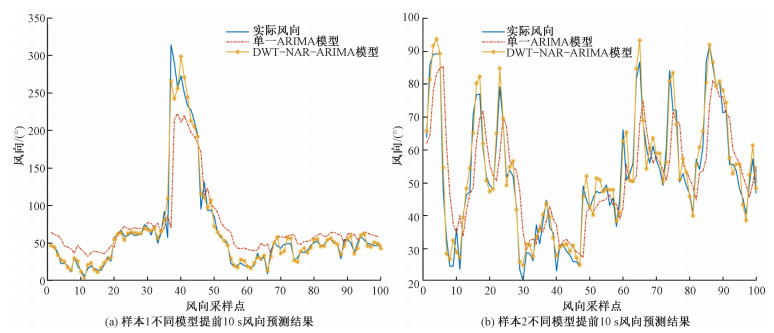
图 7和表 3展示了两组样本组合模型和单一ARIMA模型的风向预测结果及误差,图中可以看出组合模型能及时地预测到风向的突变。由于风向变化的幅值范围在0°~360°,比风速的幅值范围大很多,因此整体的均方根误差和欧式距离偏大,但组合模型仍优于单一模型,样本1和样本2的MAPE分别减少79.08%、61.68%,RMSE分别减少67.11%、64.38%。从两组样本的Pearson相关系数也可知组合模型预测出的风向序列与原始风向序列更为相似。综上可知,DWT-NAR-ARIMA组合模型能很好地适用于赛道应用场景,对赛道风速风向预测精度高且能及时捕捉到风速风向突变的发生。
|
Download:
|
| 图 7 两组样本不同模型风向预测结果 Fig. 7 Wind direction prediction results of two samples with different models | |
|
|
表 3 两组样本不同模型风向预测误差 Table 3 Wind direction prediction error of two samples with different models |
单一的风速风向预测结果不能直观地为运动员的训练提供辅助支持作用,因此对第2节组合模型所预测出的风速风向结果,需要做进一步的统计分析,将预测的风速风向大小转换为更直观的结果,与对运动员的影响结合起来,使预测结果更具实际意义。赛道风保持稳定是指风速和风向在某段时间内维持在较小水平内的变化。对于自由式滑雪空中技巧运动,一般认为风向变化维持在22.5°以内,风速变化维持在0.5 m/s以内即可称该段时间风保持稳定未发生明显变化。基于此标准,本文利用MATLAB设计一段预测后分析程序,将预测结果实现以下两类转换:
第1类依据风速预测结果统计出预测时段内风速变化强弱的占比以及出现的最大风速值。具体计算过程如下:1)计算出预测起点的前一段时间(30 s)内的平均风速,记为v;2)以该平均风速值作为判断基准,从预测起点开始,按向后的时间顺序遍历数据序列,将预测的风速值v(t)与v求差值,两者差值超出0.5 m/s范围的v(t)归为强风一类,小于等于0.5 m/s范围的归为常风一类。依据强风、常风出现的个数统计出该段时间内两种风的占比;3)遍历过程中,不断将下一个风速值与前一个风速值做比较,保留大值,遍历结束给出该段时间出现的风速最大值。
第2类依据风向预测结果统计出预测时段内风向发生大幅波动和保持稳定的概率。具体计算过程如下:1)统计出预测起点的前一段时间(30 s)内的主导风向,记为d;2)以该主导风向作为判断基准,从预测起点开始,按向后的时间顺序遍历数据序列,将预测的风向值d(t)与d求差值,两者差值的绝对值超出22.5°范围的d(t)归为风向出现波动一类,在22.5°范围内的归为风向保持稳定一类。统计出该段时间内风向波动和稳定的占比;最后将分析结果以表格的形式呈现,以上文两组样本为例,表 4展示了数据分析结果。
|
|
表 4 两组样本预测数据分析结果 Table 4 Predictive data analysis results of the two groups of samples |
经过上述转换,从表 4可以直观地判断出在样本1的预测时段内可能出现的最大风速为6.56 m/s,出现强风的概率为34%,风向出现大的波动概率为52%。而在样本2的预测时段内风速风向的稳定度更高,出现强风概率仅有13%,风向出现波动概率有32%。这样的预报信息更便于运动员对未来一段时间的赛道风速风向状况作出判断,帮助运动员在训练的过程中及时调整姿态以应对风速风向的突变,通过不断的训练能提升运动员对风速风向变化的适应能力。在赛道的某一固定站点上进行分析可以得到该位置的风稳定程度,也可以同时对赛道上5个站点的预测数据进行分析得到整个赛道上的风速风向分布特征。
4.2 模型时效分析本研究旨在极短的预测时域内得到赛道风速风向的预测结果,对于预测模型计算和训练的实时性要求高,本小节通过补充分析模型的计算用时情况,以验证其实际应用可能性。采用MATLAB的Profile功能统计出程序执行的总时间及具体每个命令分别用的时间,对耗时长的部分函数进行优化。表 5给出了不同训练样本容量下的模型平均计算用时,可以看出在不同样本容量大小下,模型的训练和建立都能在预测时域(10 s)内完成,都能满足预测实时性的要求。考虑到样本容量过小会导致模型不能充分训练,容量过大会增加读入数据和预处理的运行时间,因此,为满足赛道应用场景建模快且精度高的要求,样本容量选定在500~1 200即可,同时能满足实际应用的可能。
|
|
表 5 不同样本容量下的模型计算用时 Table 5 Model calculation time under different sample sizes |
对自由式滑雪空中技巧赛道风的准确预报能改善当前该项运动仅凭赛道旁的测风标对风场的变化进行模糊判断的现状,为运动员稳定性控制与技术训练提供辅助支持作用。
对于滑雪赛道风所具有的非平稳、波动剧烈的特点,本文采用离散小波变换对原始风速风向序列进行多尺度的小波分解以提取原始序列的各特征分量,并利用时间序列的Hurst参数估计方法对各分量的特征进行分析和判断,对长相关非线性的低频近似分量建立NAR神经网络模型,非平稳随机波动的高频细节分量建立ARIMA模型分别进行预测,再将各分量预测结果经过组合相加得到最终的预测结果。通过实验仿真与单一模型进行对比表明DWT-NAR-ARIMA组合模型能显著提高预测精度,并且有效地改善了单一模型的预测滞后性。在常用的误差评价指标基础上,引入欧几里得距离和Pearson相关系数评价预测风速序列和真实风速序列之间的距离及相似性,结果表明组合模型在获取高精度的风速风向预测值的同时具有准确及时地预测风速风向突变的能力,能很好地适用赛道应用场景,达到赛道风速风向准确预测的目的。
通过对预测结果的进一步分析,将其转换为表征赛道风稳定性的指标,以强风或常风出现概率、风向波动或稳定的概率、可能出现的最大风速直观地提供预报信息,便于运动员对赛道风速风向变化作出预判。最后对模型时效进行分析,得出本文模型平均计算用时为7.688 s,能实现实时建模,满足实际应用的需求。
后续将进一步从数据获取、建模流程、数据处理方法和提升模型训练速度等方面进行优化,使其更为系统化以此来提升实际应用价值,为自由式滑雪空中技巧这项运动助力。
| [1] |
夏娇阳, 韩秀华, 马毅, 等. 自由式滑雪运动员曲线滑道段内空气动力特性的CFD研究[J]. 天津体育学院学报, 2014, 29(3): 190-192, 202. Doi:10.13297/j.cnki.issn1005-0000.2014.03.008 |
| [2] |
刘瑞叶, 黄磊. 基于动态神经网络的风电场输出功率预测[J]. 电力系统自动化, 2012, 36(11): 19-22, 37. |
| [3] |
Sideratos G, Hatziargyriou N D. An advanced statistical method for wind power forecasting[J]. IEEE Transactions on Power Systems, 2007, 22(1): 258-265. Doi:10.1109/TPWRS.2006.889078 |
| [4] |
An X L, Jiang D X, Zhao M H, et al. Short-term prediction of wind power using EMD and chaotic theory[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(2): 1036-1042. Doi:10.1016/j.cnsns.2011.06.003 |
| [5] |
Costa A, Crespo A, Navarro J, et al. A review on the young history of the wind power short-term prediction[J]. Renewable and Sustainable Energy Reviews, 2008, 12(6): 1725-1744. Doi:10.1016/j.rser.2007.01.015 |
| [6] |
Kusiak A, Zheng H Y, Song Z. Short-term prediction of wind farm power: a data mining approach[J]. IEEE Transactions on Energy Conversion, 2009, 24(1): 125-136. Doi:10.1109/TEC.2008.2006552 |
| [7] |
Mathieu A, Lahellec A, Weill A. Evaluation of a numerical weather forecast model using boundary layer cloud-top temperature retrieved from AVHRR[J]. Monthly Weather Review, 2004, 132(4): 915-928. Doi:10.1175/1520-0493(2014)132〈0915:EOANWF〉2.0.CO;2 |
| [8] |
丁藤, 冯冬涵, 林晓凡, 等. 基于修正后ARIMA-GARCH模型的超短期风速预测[J]. 电网技术, 2017, 41(6): 1808-1814. Doi:10.13335/j.1000-3673.pst.2016.2357 |
| [9] |
Chen P Y, Pedersen T, Bak-Jensen B, et al. ARIMA-based time series model of stochastic wind power generation[J]. IEEE Transactions on Power Systems, 2010, 25(2): 667-676. Doi:10.1109/TPWRS.2009.2033277 |
| [10] |
Torres J L, García A, de Blas M, et al. Forecast of hourly average wind speed with ARMA models in Navarre (Spain)[J]. Solar Energy, 2005, 79(1): 65-77. Doi:10.1016/j.solener.2004.09.013 |
| [11] |
Erdem E, Shi J. ARMA based approaches for forecasting the tuple of wind speed and direction[J]. Applied Energy, 2011, 88(4): 1405-1414. Doi:10.1016/j.apenergy.2010.10.031 |
| [12] |
王小娟, 刘俊霞, 胡兵, 等. 基于CS-SVR模型的短期风电功率预测[J]. 计算机测量与控制, 2020, 28(1): 152-155. Doi:10.16526/j.cnki.11-4762/tp.2020.01.032 |
| [13] |
王晓兰, 王明伟. 基于小波分解和最小二乘支持向量机的短期风速预测[J]. 电网技术, 2010, 34(1): 179-184. Doi:10.13335/j.1000-3673.pst.2010.01.008 |
| [14] |
彭春华, 刘刚, 孙惠娟. 基于小波分解和微分进化支持向量机的风电场风速预测[J]. 电力自动化设备, 2012, 32(1): 9-13. Doi:10.3969/j.issn.1006-6047.2012.01.002 |
| [15] |
刘爱国, 薛云涛, 胡江鹭, 等. 基于GA优化SVM的风电功率的超短期预测[J]. 电力系统保护与控制, 2015, 43(2): 90-95. |
| [16] |
Büyükşahin Ü Ç, Ertekin. Improving forecasting accuracy of time series data using a new ARIMA-ANN hybrid method and empirical mode decomposition[J]. Neurocomputing, 2019, 361: 151-163. Doi:10.1016/j.neucom.2019.05.099 |
| [17] |
赵辉, 华海增, 岳有军, 等. 基于互补集合经验模态分解-模糊熵-深度信念网络的短期风速预测[J]. 科学技术与工程, 2019, 19(29): 137-143. Doi:10.3969/j.issn.1671-1815.2019.29.022 |
| [18] |
李华, 任艺迪, 谷瑞政, 等. 基于花朵授粉算法的组合式风速预测[J]. 科学技术与工程, 2020, 20(4): 1436-1441. Doi:10.3969/j.issn.1671-1815.2020.04.021 |
| [19] |
颜宏文, 卢格宇. CEEMD-WT和CNN在短期风速预测中的应用研究[J]. 计算机工程与应用, 2018, 54(9): 224-230. |
| [20] |
杨正瓴, 刘阳, 张泽, 等. 采用最近历史观测值和PLSR进行空间相关性超短期风速预测[J]. 电网技术, 2017, 41(6): 1815-1822. Doi:10.13335/j.1000-3673.pst.2016.2295 |
| [21] |
陈妮亚, 钱政, 孟晓风, 等. 基于空间相关法的风电场风速多步预测模型[J]. 电工技术学报, 2013, 28(5): 15-21. Doi:10.19595/j.cnki.1000-6753.tces.2013.05.002 |
| [22] |
李文良, 卫志农, 孙国强, 等. 基于改进空间相关法和径向基神经网络的风电场短期风速分时预测模型[J]. 电力自动化设备, 2009, 29(6): 89-92. Doi:10.3969/j.issn.1006-6047.2009.06.020 |
| [23] |
王东风, 王富强, 牛成林. 小波分解层数及其组合分量对短期风速多步预测的影响分析[J]. 电力系统保护与控制, 2014, 42(8): 82-89. |
| [24] |
田中大, 李树江, 王艳红, 等. 基于小波变换的风电场短期风速组合预测[J]. 电工技术学报, 2015, 30(9): 112-120. Doi:10.19595/j.cnki.1000-6753.tces.2015.09.015 |
| [25] |
姜丽霞, 王晾晾, 吕佳佳, 等. 基于Hurst指数的黑龙江省作物生长季降水趋势研究[J]. 气象与环境学报, 2020, 36(2): 70-77. Doi:10.3969/j.issn.1673-503X.2020.02.009 |
| [26] |
潘雅婧, 王仰麟, 彭建, 等. 基于小波与R/S方法的汉江中下游流域降水量时间序列分析[J]. 地理研究, 2012, 31(5): 811-820. |
| [27] |
Han Z T, Cheng M Z, Chen F X, et al. A spatial load forecasting method based on DBSCAN clustering and NAR neural network[J]. Journal of Physics: Conference Series, 2020, 1449(1): 012032. Doi:10.1088/1742-6596/1449/1/012032 |
| [28] |
Wei S K, Zuo D P, Song J X. Improving prediction accuracy of river discharge time series using a Wavelet-NAR artificial neural network[J]. Journal of Hydroinformatics, 2012, 14(4): 974-991. Doi:10.2166/hydro.2012.143 |
| [29] |
葛宇生. 基于NAR动态神经网络后验信息的概率水文预报[D]. 哈尔滨: 东北农业大学, 2016.
|
| [30] |
向小东, 黄飘. 基于EEM D-NAR的突发传染病舆情热度预测研究[J]. 武汉理工大学学报(信息与管理工程版), 2019, 41(4): 352-358. Doi:10.3963/j.issn.2095-3852.2019.04.002 |
 2022, Vol. 39
2022, Vol. 39 


