2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
近年来,随着卫星通信网络的快速发展,接入用户呈海量增长,低轨卫星(LEO卫星)由于星地链路时延小,对天线功率和尺寸要求更低而广受青睐[1]。目前卫星通信系统可用频率资源非常有限,包括S频段上下行链路的2×15 MHz和Ka频段上下行链路的2×2 500 MHz[2]。此外,相较于地面蜂窝网络,低轨卫星上的功率资源有限,当卫星的太阳能电池板位于阴影处时,卫星只能使用电池能源。因此,合理调配资源,提高卫星频带效率(spectrum efficiency,SE)和能效(energy efficiency,EE)是当前的研究热点。如何智能化、实时化的合理调度星上资源成为低轨卫星通信系统研究中的热点之一。
宽带通信卫星多采用多波束技术,通过波束间频率复用、功率分配等技术可以显著提高系统容量。对于卫星多波束功率分配,传统的固定分配方式已无法适应高能效的发展需求,目前许多研究都开始考虑卫星在空间、时间以及其传播路径的变化,功率分配方式逐渐向自适应动态分配方式发展。文献[3]根据流量需求和信道条件,使用拉格朗日乘数法优化了功率分配,但未考虑同频信道干扰。文献[4]考虑同频信道干扰,证明功率分配问题的NP-hard特性,并由此激发提出启发式算法,将问题转化成两阶段优化模型。文献[5]研究了多波束卫星通信系统载波和功率的联合分配算法,使系统在总发射功率限定下能满足更多用户需求。文献[6]将资源分配问题分解为功率分配、带宽分配和对偶变量更新3个问题,提出对应分配算法,结果能有效提升系统容量。但以上两篇文献的方法没有对信道进行建模,不适合低轨卫星时变信道环境。文献[7]利用动态规划方法讨论了卫星网络中的最优功率分配问题,然而文中每个用户的能量消耗是以已知的概率分布产生的,而实际上是随机事件,具有一定的局限性。
上述研究成果大多集中在同步轨道卫星的多波束功率分配,用户位置相对静态,信道状态相对固定,算法更新频率不需要很高。而低轨卫星运动速度快,过顶时间短,具有高动态性,用户与接入卫星的相对位置在实时变化,复杂度高的启发式算法收敛速度慢,效率低。
当前,机器学习在卫星无线资源分配的研究尚处于探索阶段,深度强化学习以其自主决策方面的优势在资源分配研究中取得显著成效,例如文献[8]采用深度Q学习方案联合优化星地网络中的缓存、计算和网络资源,提升了资源利用率。
本文提出一种基于深度强化学习的面向低轨卫星的功率分配方法,对卫星下行链路进行信道建模,考虑噪声和同频干扰的影响。同时考虑卫星的动态特性,并对其建模,将卫星在轨运行过程进行时间切片划分,每进入一个时间切片,更新信道信息。利用深度强化学习动态分配各个波束子载波的功率,在不了解网络环境动态特性的情况下,本文选择无模型(model-free)的强化学习方法,解决该序列决策问题,针对性地设计强化学习的状态、动作和奖励函数,从而有效提升系统总容量。为了提升算法速度,降低硬件存储消耗,对功率值离散化处理。该方案能充分利用强化学习的决策能力和深度学习的感知能力。
1 系统模型 1.1 多波束卫星覆盖模型3GPP在非地面网络与地面5G融合的场景下提出星地融合的4种网络架构[9],本文采用无弯管、卫星承载gNB(下一代NodeB)并与用户直连的架构。卫星通过多波束技术可以进行频率复用,提高系统容量,同时能让能量更加集中。本文针对使用同一频段的多个波束,下行链路采用OFDM传输模式,同一波束内用户之间没有干扰,不同波束之间产生不同程度的同频干扰,这种简化降低了模型的复杂度,一般也不影响模型的有效性。用户在波束覆盖范围内随机分布。
假设卫星上搭载的信息控制中心可以收集所有的波束信息,包括链路的信号噪声干扰比(signal noise and interference ratio,SNIR)和传输功率。在时隙t接入波束k的用户数量表示为
| $ u_t^k \in \left\{ {M_t^1, \cdots M_t^k, \cdots M_t^K} \right\}\left( {\sum {_{k = 1}^K} M_t^k = M} \right), $ | (1) |
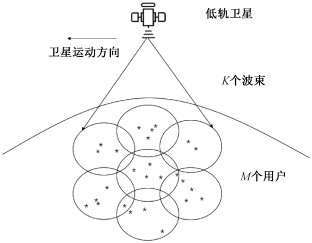
其中Mtk是时刻t接入波束k的用户数量,M是总的用户接入数量,K是卫星波束总个数。波束的地理分布如图 1所示,圆表示波束的3 dB衰减边界。每个波束可以使用N个正交子载波。一旦有用户接入波束,该波束被激活并且传输功率为ptn,每个用户可以在时刻t连接到一个波束。每个子载波只能被分配给单个用户。信道模型采用自由空间损耗模型。
|
Download:
|
| 图 1 低轨多波束卫星覆盖模型 Fig. 1 LEO multibeam satellite coverage model | |
在时刻t, 自由空间传播损耗为L, L=4πd/λ2,其中d为信号传输距离, λ是信号波长[10]。用pt(k, n)和pt(k′, n)分别表示第k个波束和第k′个波束中第n个子载波对用户m的传输功率,则第k个波束中第n个子载波的有用信号功率Et(k, n)和干扰信号功率It(k, n)可以表示成
| $ E_{t}^{(k, n)}=p_{t}^{(k, n)} G_{k, m}\left(\frac{\lambda^{2}}{4 \pi d}\right)=h_{k, m}^{n} p_{t}^{(k, n)}, $ | (2) |
| $ I_{t}^{(k, n)}=\sum\limits_{k^{\prime} \neq k} p_{t}^{\left(k^{\prime}, n\right)} G_{k^{\prime}, m}\left(\frac{\lambda^{2}}{4 \pi d}\right)=\sum\limits_{k^{\prime} \neq k} h_{k^{\prime}, m}^{n} p_{t}^{\left(k^{\prime}, n\right)}. $ | (3) |
因此,第k个波束中第n个子载波对用户m的信道增益计算式为
| $ h_{k, m}^{n}=G_{k, m}\left(\frac{\lambda^{2}}{4 \pi d}\right), $ | (4) |
波束增益Gk, m由下式计算:
| $ G_{k, m}=G_{\max }\left(\frac{J_{1}(u)}{2 u}+36 \frac{J_{3}(u)}{u^{3}}\right)^{2}. $ | (5) |
u=2.071 23sinθk, m/sinθ3dB, Gmax是多波束卫星天线的最大增益,θ是波束中心与用户终端之间的夹角。hk, m(n)表示第k个波束中第n个子载波对用户m的信道增益,J1和J3分别表示第一类一阶和三阶贝塞尔函数[11]。
让ξt(k, n, m)表示时刻t,卫星的第k个波束服务于用户m的第n个子载波的SINR,其中n∈{1, …, N},信干比SINR表示为
| $ \xi _t^{(k, n, m)} = \eta _t^{(k, m)}\frac{{h_{k, m}^{(n)}p_t^{(k, n)}}}{{\sum\limits_{{k^\prime } \ne k} {h_{{k^\prime }, m}^{(n)}} p_t^{\left( {{k^\prime }, n} \right)} + {\sigma ^2}}}. $ | (6) |
由于采用全频率复用,干扰来自其他所有波束。ηt(k, m)表示用户m是否连接到第k个波束,ηt(k, m)∈[0, 1],σ2是噪声功率。
1.3 问题表述系统性能由总体容量衡量,单位bps/Hz。波束在时刻t,在子载波n和用户连接的容量由下式给出
| $ C_{t}^{k, n}=\frac{B}{N} \log _{2}\left(1+\sum\limits_{m=1}^{M} \xi_{t}^{(k, n, m)}\right), $ | (7) |
整个容量可以定义为
| $ S C_{t}=\sum\limits_{n=1}^{N} \sum\limits_{k=1}^{K} C_{t}^{k, n}, $ | (8) |
目标是通过调整波束在子载波上的功率提升整个网络的总体容量
| $ \boldsymbol{p}_{t}^{k}=\left[p_{t}^{k, 1}, \cdots p_{t}^{k, n} \cdots p_{t}^{(k, N)}\right]. $ | (9) |
优化问题可以表述为以下
| $ \left\{\begin{array}{c} \operatorname{argmax} S C_{t} \\ \text { s.t. } p_{t}^{(k, n)} \geqslant p_{\min }, \forall n, k \\ \sum\limits_{n, k} p_{t}^{(k, n)} \leqslant p_{\max }, \forall n, k \end{array}\right., $ | (10) |
其中pmax是卫星的最大传输功率,各个波束总功率不能大于卫星最大功率,pmin是子载波的最小传输功率。
在网络初始化阶段,用户基于最大SINR准则完成和卫星波束的连接。用户和波束的链路干扰主要来自同频干扰,链路速率受附近波束到用户的信号强度的影响。本文的目标是调整波束中各个子载波的传输功率,从而提升整个低轨卫星的系统容量。考虑到用户的公平性,本文将下行带宽平均分配给用户,子载波的初始功率也由总功率平均分配。
上述问题是一个非凸优化问题,解决该问题的传统方法是启发式搜索,然而大多数这类算法运行时间长效率低,难以实时在线调整[12],由于低轨卫星的动态特性,某一时刻分配的最优功率值在下一时刻不一定是最优的。为了解决该问题,引入深度强化学习算法。
2 基于深度强化学习的功率分配 2.1 信道统计信息的获取时间划分为了适应低轨卫星的高速移动特性,需要高频率的收集当前卫星的轨道参数和信道增益信息,以计算公式(4),再根据这些信息调整各个波束子载波功率值,而信息获取时间间隔的大小会影响功率分配方案的合理性,本文根据以下原则划分时间间隔。
星地信道主要受大尺度影响,即主要考虑路径损耗的影响,卫星和地面终端节点之间的路径损耗4πd/λ2写成dB形式为
| $ L=92.44+\lg f+20 \lg d, $ | (11) |
其中:f为卫星中心频率,d为信号传输距离。将卫星运行过程划分成若干时隙,在每个时隙中,可以将信道视为不变。因此时隙的间隔只要充分小就可以假设路径损耗在该时隙内不发生改变。
时隙划分足够小需满足以下条件
| $ [L(t+\Delta t)-L(t)] / L(t) \ll1. $ | (12) |
此外,卫星运动也会影响终端用户相对波束中心的位置,时隙的划分需满足以下条件
| $ \boldsymbol{v} \cdot \Delta t / 2 r\ll1, $ | (13) |
其中:v是卫星星下点的运动速度,r是单个波束在地面的投影半径。
低轨卫星在轨道上持续运动,难以实现连续的子载波功率调整来适应其动态特性。将低轨卫星在轨运行的连续时间划分成若干离散时隙,通过上述时隙划分合理性的讨论,可以假设卫星相对地面终端的距离和信道状态信息不变,子载波在该时隙内维持固定的功率分配值。时隙改变后,卫星位置等状态信息发生改变,则改变功率分配值。该方案能够简化低轨卫星的动态特性。
2.2 功率分配的Q学习方案传统的功率分配方法通常利用先验知识进行决策,在复杂环境下效果不佳。由于每个时隙的功率分配操作只取决于卫星波束覆盖的当前状态而不是历史状态,因此低轨多波束卫星的功率分配可以建模成马尔科夫决策过程。由于信道条件是时变的,采用无模型强化学习算法——Q学习算法, 在转移概率未知情况下,Q学习算法能够提高决策能力。一个典型的强化学习框架由智能体和环境组成,两者通过智能体的动作、环境的状态和奖励相互作用。在低轨卫星功率分配场景下,每个波束作为一个智能体,通过连续迭代使Q值收敛。状态、动作和奖励函数定义如下:
1) 状态空间:sk, n={Mk, ptk},其中Mk表示接入波束的用户数量,ptk表示波束的功率等级。为了降低算法的复杂度和网络的状态空间,将功率值划分成若干离散等级。离散规则如下:
2) 动作:在马尔科夫决策过程中,智能体根据系统状态sk, n进行决策,动作决策应该满足约束条件,动作设计由如下二元组构成
| $ \boldsymbol{A}=\left\{a_{1}, a_{2}, \cdots a_{3 N} \mid a_{k}=\left(n_{k}, \Delta p_{t}^{k, n}\right)\right\}, $ | (14) |
其中: nk表示第k个波束的第n个子载波, Δptk, n表示子载波的功率调整量。由于子载波有N个,功率调整量有3种选择(包括增加、减少和不变),故动作共有3N种选择。
| $ \Delta p_{t}^{k, n} \in\left\{-\left|\Delta p_{t}^{k, n}\right|, 0, +\left|\Delta p_{t}^{k, n}\right|\right\}. $ | (15) |
对于子载波所服务用户附近的h个用户,若增加功率后这h个用户的总体容量Cth增加,则采取动作为
3) 奖励函数:Q学习过程中,智能体需要通过决策获得最大的累计回报,奖励值在智能体采取动作后通过奖励函数计算获得,奖励函数设计越接近优化目标,越能达到更好的性能。该场景下,智能体采取动作后,应使吞吐量增加,同时波束总功率小于卫星最大功率,基于该原则第k个波束在第n个子载波上的奖励定义如下所示:
| $ r_{ct}^k = \left\{ {\begin{array}{*{20}{c}} {\sum\limits_{n = 1}^N 1 - {{\rm{e}}^{ - \left( {c_t^{(k, n)}} \right)}}, }&{\sum\limits_{n = 1}^N {p_t^{k, n}} < {P_{\max }}}\\ { - 1, }&{{\rm{ Otherwise }}} \end{array}} \right.. $ | (16) |
此外,为了保证用户QoS,可引入服务阻塞率。用户速率若小于设置的传输速率阈值Cth,则判定为阻塞,服务阻塞率定义为用户阻塞个数Nbk与总用户Nus之比,即pbk=Nbk/Nus。
引入阻塞率后的奖励函数定义为
| $ r_{t}^{k}=\beta_{1} r_{c t}^{k}+\beta_{2} r_{b t}^{k}, $ | (17) |
其中: rbtk=e-pbk,阻塞率越低,奖励值越高;β1和β2是权重因子。
4) Q学习迭代过程:单个波束通过连续的迭代学习更新行为价值函数。行为价值函数由一个Q值表Q(s, a)表示,其中a属于动作集合A,s属于状态集合。Q(s, a)表示在状态s执行动作a时,从一个无限时间的角度计算累计奖励值的期望值,Q值更新方式具体如下
| $ \begin{array}{l} Q\left( {{s_t}, {a_t}} \right) = (1 - \alpha )Q\left( {{s_t}, {a_t}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha \left[ {{r_{t + 1}} + \gamma \mathop {\max }\limits_a Q\left( {{s_{t + 1}}, a} \right)} \right], \end{array} $ | (18) |
其中:Rt+1表示在状态St采取动作at后的即时奖励值。
由于低轨卫星的动态特性,尽管对功率值做了离散化处理,波束覆盖网络的状态空间仍然很大,并且每个智能体的Q值表不同。因此,采用动态状态添加方法,只有当新状态出现,该状态才会被自动添加到状态表。
Q学习算法根据过去出现过的状态,统计和迭代Q值。一方面Q学习适用的状态和动作空间非常小;另一方面Q学习泛化能力差。
2.3 功率分配的深度强化学习(DQN)方案Q学习算法的值函数是通过Q值表进行更新的,而深度Q学习(deep Q-network, DQN)通过神经网络的参数更新来进行值函数更新[13]。更新方式采用了梯度下降算法,值函数更新如下
| $ \begin{aligned} w_{t+1}=& w_{t}+\alpha \frac{1}{U_{m b}} \sum{ }_{i=1}^{U_{m b}}\left[r+\gamma \max _{a} Q^{-}\left(s, a ; w^{-}\right)-\right.\\ & Q\left(s_{i}, a_{i} ; w\right] \nabla Q\left(s_{i}, a_{i} ; w\right) \end{aligned} $ | (19) |
其中: r+γmaxQ-(s, a; w-)是时序差分目标, Q-(s, a; w-)是通过值函数近似的网络目标;Umb是批量更新的大小。
引入深度神经网络拟合Q值表,该网络包含4层神经层,输入层包含接入第k个波束的用户m所占用的子载波n的信道状态信息。中间的两个隐藏层主要增加网络优化的非线性,提高网络的适应能力。输出层包含所有动作对应的Q值。神经网络基本结构如图 2所示。

|
Download:
|
| 图 2 DQN神经网络的基本结构 Fig. 2 Basic structure of DQN neural network | |
利用目标网络Q-计算标签值,作为学习的目标,标签值yt计算式为
| $ y_{t}=\left\{\begin{array}{cc} r_{t}, & a_{t+1}=\varnothing \\ r_{t}+\gamma \max _{a} Q^{-}\left(s, a ; w^{-}\right), & \text {others } \end{array} .\right. $ | (20) |
损失函数计算采用以下方式:
| $ L(w)=E\left(y_{t}-Q(w)\right)^{2}+c\|w\|_{2}, $ | (21) |
其中:Q(s, a)是Q学习计算得出的功率分配策略,由公式(17)迭代训练获得。损失函数第一部分是为了使神经网络尽可能拟合Q值表,第二部分是正则化项,约束参数w避免网络过拟合, c是惩罚因子,c∈(0, 1)。利用随机梯度下降法Adam优化算法进行训练,来最小化损失函数L(w)。
除了对参数正则化处理,网络隐藏层以固定概率随机丢弃一部分节点,提高网络结构的多样性,进一步防止网络过拟合[14]。
基于深度强化学习的低轨卫星功率分配方案的架构如图 3所示。

|
Download:
|
| 图 3 低轨卫星功率分配的DQN方案架构 Fig. 3 DQN scheme architecture for LEO satellite power allocation | |
本文提出的基于DQN的功率分配算法具体实现如下:
1) 初始化阶段
① 初始化通信场景,建立低轨卫星多波束网络覆盖模型。初始化信道参数、时隙长度、用户和卫星位置更新参数。
② 初始化DQN方案中的相关参数。低轨卫星上搭载的信息控制中心设定学习速率α,折扣因子γ,初始探索概率ε。设置训练网络的周期数Nepochs、经验池大小Umax、训练数量Ust、采样大小Umb、时隙计数器Nc、目标网络更新时隙间隔D。
③ 平均分配初始化功率。
2) 训练和运行阶段
① 设置循环周期epoch=1。每执行一遍循环过程(循环过程包括下面步骤(2)至(5)),epoch计数加1,直到循环Nepochs次停止。
② 信息控制中心观测状态st,即此时连接到各波束的用户数量和各波束的功率等级。波束以ε的概率随机选取动作at,即对任意子载波调节功率;以1-ε的概率选取最优动作at,选取子载波调整功率。获得新状态st+1,依据式(16)或式(17)计算状态的即时奖励,采用式(16)的算法记为最优DQN算法,采用式(17)的算法记为公平DQN算法。将(st, at, rt, st+1)4元组存储到经验池中,若经验池的容量超过Umax,则丢弃最早的4元组。
③ 当循环周期epoch满足条件:epoch>Ust时,从经验池中随机抽取Umb个样本,由式(20)计算标签值,根据式(21)计算损失值L(w),用Adam优化算法训练当前Q网络并更新权值w。
④ 当mod(t, D)=0时(即每经过D个时隙),更新目标网络Q-参数w-=w。
⑤ 当前时隙t的计数增1,进入下一时隙,若t>Nc,停止本轮循环,执行下一步骤,否则继续转步骤②执行。
⑥ 更新循环周期epoch,增加1,若epoch>Nepochs,停止循环,输出已经训练好的当前Q网络进行动作决策,否则继续转步骤②执行。
3 仿真分析 3.1 仿真场景和参数设置仿真场景由若干卫星波束和随机分布在卫星波束覆盖区域的用户组成。在波束重叠区域每个用户根据最大SINR连接到卫星。假设噪声功率为σ2=10-7 W。考虑到地面用户终端的移动速度远远小于卫星的移动速度,例如卫星在780 km轨道高度时,运行速度7.46 km/s,因此可以忽略用户的移动性。卫星波束在地面的覆盖区域朝一定方向以固定速度移动,因此仿真可以将卫星位置的移动过程转换成用户位置在卫星波束覆盖区域中的移动。用户朝一定方向以和卫星的相对速度运动,移出卫星覆盖范围的用户,在反方向随机新增相同用户数,位置在每个时隙更新一次。仿真参数设置参考现有低轨卫星通信技术[15-17],具体参数设置如表 1所示。仿真运算依托Python语言和Pycharm编译环境运行,使用Keras库对模型进行构建和训练。
|
|
表 1 参数配置 Table 1 Parameter configuration |
时隙长度为4 s,根据卫星轨道参数计算结果如下, 满足时隙足够小的条件:
| $ \begin{gathered} {[L(t+\Delta t)-L(t)] / L(t) \approx 0}, \\ v \cdot \Delta t / 2 r=0.096. \end{gathered} $ |
根据波束个数和子载波个数DQN输入参数个数为5 328,设置隐藏层1参数8 000,参数丢弃率0.5,隐藏层2参数4 000,参数丢弃率0.4,输出层参数1 536个。
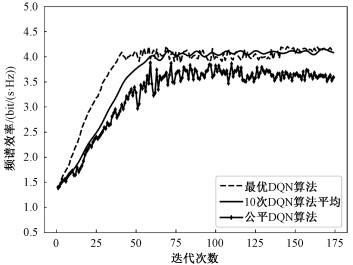
3.2 仿真结果及分析为了体现所提功率分配方案的性能,多次计算最优DQN算法的收敛曲线并做平均。图 4显示模型收敛过程的频谱效率。对于每一次迭代,每过4 s更新时隙,用户和卫星位置改变,信道环境随之更新,结果中虚线表示最优DQN算法单次收敛过程,黑色实线表示10次DQN算法收敛过程的平均结果。由图像可见深度强化学习算法通过多轮迭代在收敛之后能够达到较高的频谱效率。并且收敛速度较快,从10次算法的运行结果统计来看,卫星经过约60次迭代就能使算法收敛,可达到稳定高效的频谱效率,平均约4.12 (bit/(s ·Hz))。在少数情况下,如用户初始位置不同,经过约50次迭代就能使算法接近收敛。公平DQN算法权重因子β1=0.7,β2=0.3,相比最优DQN算法其收敛速度更慢,曲线波动更大。
|
Download:
|
| 图 4 算法收敛图像 Fig. 4 Algorithm convergence image | |
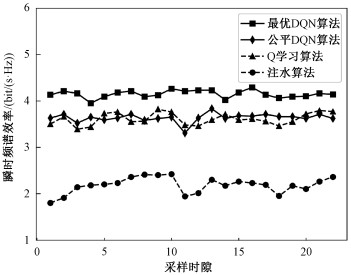
为了分析所提功率分配算法的有效性,对本文所提的两种DQN算法和Q学习算法、注水功率分配算法进行对比[18],如图 5所示。在每个时隙计算一次系统的频谱效率。注水算法的基本思想是对信道条件好的多分配功率,对信道条件差的少分配功率,没有考虑同频信道干扰,也忽略了用户的位置分布。可以看出最优DQN算法的瞬时频谱效率明显更高,也更加稳定。
|
Download:
|
| 图 5 4种方案的频谱效率对比 Fig. 5 Comparison of spectrum efficiency of four solutions | |
仿真实验还统计了各个算法对应的用户阻塞率。其中,公平DQN算法通过奖励函数的设计尽量保证每个用户的速率不低于一个阈值。实验结果如表 2所示。可以看出,公平DQN算法在奖励函数设计中考虑用户阻塞率后,相比最优DQN算法整体频谱效率有所降低,但是阻塞率变得更小,保证了一定的公平性。并且公平DQN算法的频谱效率仍然高于注水算法和Q学习算法。注水功率分配则将大部分功率分配给了信道增益较大的用户。
|
|
表 2 用户阻塞率对比 Table 2 The comparison of user blocking probability |
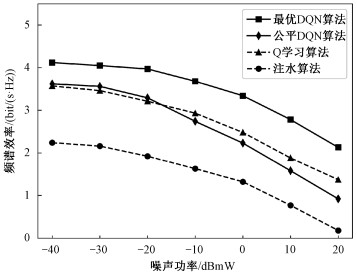
最后,比较了各个算法在不同噪声功率环境下的频谱效率,如图 6所示。其中,公平DQN算法和注水算法的频谱效率随着噪声功率的升高下降更快,注水功率算法在噪声较高时频谱效率会受到严重的影响。
|
Download:
|
| 图 6 不同噪声功率下的频谱效率 Fig. 6 Spectrum efficiency under different noise power values | |
本文针对低轨卫星的功率分配问题,提出一种基于深度强化学习的解决方案,将卫星运动过程进行时隙划分,以单个时隙作为强化学习训练过程中的单步,提取该时隙中的用户位置、信道增益信息,并对时隙大小进行了合理划分。进一步针对性地设计强化学习的状态、动作和奖励函数,引入深度神经网络加速收敛。为了减少状态空间,降低算法复杂度,对功率值进行了离散化处理。
在具体仿真场景下验证算法的性能,结果显示,相对功率注水算法,在带宽固定情况下,本方案能明显提升系统容量,即提升了频谱效率,可以满足更大的流量需求,适用于数据业务。在引入服务阻塞率后,所提方案能在一定程度上降低阻塞率,且频谱效率依然较高,该方案为低轨卫星通信系统资源分配提供了一种思路。
| [1] |
汪春霆, 李宁, 翟立君, 等. 卫星通信与地面5G的融合初探(一)[J]. 卫星与网络, 2018(9): 14-21. Doi:10.3969/j.issn.1672-965X.2018.09.004 |
| [2] |
汪春霆, 李宁, 翟立君, 等. 卫星通信与地面5G的融合初探(二)[J]. 卫星与网络, 2018(11): 22-26, 28. Doi:10.3969/j.issn.1672-965X.2018.11.005 |
| [3] |
Choi J P, Chan V W S. Optimum power and beam allocation based on traffic demands and channel conditions over satellite downlinks[J]. IEEE Transactions on Wireless Communications, 2005, 4(6): 2983-2993. Doi:10.1109/TWC.2005.858365 |
| [4] |
Alexis I, Shankar B, Arapoglou P, et al. Power allocation in multibeam satellite systems: A two-stage multi-objective optimization[J]. IEEE Transactions on Wireless Communications, 2015, 14(6): 3171-3182. Doi:10.1109/TWC.2015.2402682 |
| [5] |
Nakahira K, Kobayashi K and Ueba M. Capacity and quality enhancement using an adaptive resource allocation for multi-beam mobile satellite communication systems[C]//IEEE Wireless Communications and Networking Conference WCNC 2006. April 3-6, 2006, Las Vegas, NV, USA: IEEE, 2006: 153-158. DOI: 10.1109/WCNC.2006.1683456.
|
| [6] |
史煜, 张邦宁, 郭道省, 等. 考虑波束间干扰的多波束卫星功率带宽联合分配算法[J]. 计算机工程, 2018, 44(2): 103-106, 113. Doi:10.3969/j.issn.1000-3428.2018.02.018 |
| [7] |
Fu A C, Modiano E, and Tsitsiklis J. Optimal energy allocation and admission control for communications satellites[J]. IEEE/ACM Transactions on Networking, 2003, 11(3): 488-500. Doi:10.1109/TNET.2003.813041 |
| [8] |
Qiu C, Yao H, Yu F R, et al. Deep Q-learning aided networking, caching and computing resources allocation in software-defined satellite-terrestrial networks[J]. IEEE Transactions on Vehicular Technology, 2019, 68(6): 5871-5883. Doi:10.1109/TVT.2019.2907682 |
| [9] |
3GPP. Study on New Radio (NR) to support non terrestrial networks (Release 15): 3GPP TR 38.811 [S/OL]. (2018-8-10) [2020-6-20]. https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3234.
|
| [10] |
Ippolito L J, Joseph L. Satellite communications systems engineering: atmospheric effects, satellite link design and system performance[M]. Chichester, UK: John Wiley & Sons, 2017.
|
| [11] |
Christopoulos D, Chatzinotas S, Zheng G, et al. Linear and nonlinear techniques for multibeam joint processing in satellite communications[J]. EURASIP Journal on Wireless Communications and Networking, 2012, 162(2012): 1-13. Doi:10.1186/1687-1499-2012-162 |
| [12] |
刘帅军. 卫星通信系统中动态资源管理技术研究[D]. 北京: 北京邮电大学, 2018.
|
| [13] |
Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533. Doi:10.1038/nature14236 |
| [14] |
Srivastava N, Hinton G E, Krizhevsky A, et al. Dropout: a simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research, 2014, 15(1): 1929-1958. |
| [15] |
翟继强, 李雄飞. OneWeb卫星系统及国内低轨互联网卫星系统发展思考[J]. 空间电子技术, 2017, 14(6): 1-7. Doi:10.3969/j.issn.1674-7135.2017.06.001 |
| [16] |
Pratt S R, Raines R A, Fossa C E, et al. An operational and performance overview of the IRIDIUM low earth orbit satellite system[J]. IEEE Communications Surveys, 1999, 2(2): 2-10. Doi:10.1109/COMST.1999.5340513 |
| [17] |
赵星惟, 吕源, 刘会杰, 等. LEO通信卫星多波束天线构型方案设计[J]. 中国科学院研究生院学报, 2011, 28(5): 636-641. Doi:10.7523/j.issn.2095-6134.2011.5.011 |
| [18] |
张冬梅, 徐友云, 蔡跃明. OFDMA系统中线性注水功率分配算法[J]. 电子与信息学报, 2007, 29(6): 1286-1289. |
 2022, Vol. 39
2022, Vol. 39 


