商品期货的收益率与股票相比呈现较为不同的时间序列属性，可以显著提高投资组合的分散化效果，因此，商品期货在现代组合管理中扮演着越来越重要的角色。如今，基于动量效应的动量策略正在被广泛应用于投资组合管理当中。自从Jegadeesh和Titman^[1]发掘动量效应并据此构建动量策略以来，这一可以获得超额收益但其收益无法完全被Fama-French五因子模型所解释的策略越来越广泛地使用到组合管理理论与实务当中，并且一直都是金融市场与行为金融研究中的重要课题之一。尽管目前动量策略获取显著收益的机理在学界尚未形成统一的结论，但20世纪之后，动量策略凭借实践有效性在实际投资的操作和投资组合管理过程中被广泛地应用和配置，黄静和高飞^[2]研究发现90 % 的基金经理都倾向使用动量策略进行投资实践和组合配置。

文献研究的过程中发现，关于对动量崩溃(momentum crashes)进行定量解释及风险管理的研究已经逐渐兴起。近年来，有学者发现在某些极端的市场环境下，尤其在市场持续下跌后出现突然反弹，并且事前市场波动率处于较高水平时，动量策略的收益倾向于出现极端收益和收益率分布负偏现象，这种现象被定义为动量崩溃^[3]。Barroso和Santa-Clara^[4]研究指出与市场因素、规模因素、价值因素相比，在相同的样本空间上对动量因子的风险敞口可以获得最高的夏普比率，然而一旦发生极端的市场环境导致动量崩溃的发生，动量因子带来的收益却是最低的，如果能够做到对动量崩溃的管理，则可进一步提升动量策略的收益能力。Daniel和Moskowitz^[3]研究了包括美国股市、全球其他国家股市、美国商品期货市场、外汇市场等其他资产在内的各大类资产时，发现均存在一定的动量崩溃风险。然而在这一研究领域，国内对于动量崩溃的定量研究及其风险管理较少，相关理论和实践的研究仍处于起步阶段。

因此，针对国内商品期货市场动量崩溃现象的存在性及其定量研究对动量策略的风险管理具有理论指导意义和研究价值，针对动量崩溃带来的风险提出具有可行性的风险管理手段对市场具有实践价值。此次新冠疫情席卷全球，各类资产在避险和恐慌情绪的主导下，出现不同程度的抛售和流动性危机，资产价格短期内出现大幅下跌，极端行情推高市场波动率的同时无疑会给动量策略的收益带来极大的负面影响。面对当前和未来可能发生的“黑天鹅”事件，研究动量崩溃风险管理显得尤为突出。对于广泛使用的动量策略，为了规避动量崩溃发生带来动量策略的极端损失和动量收益的大幅回撤，就动量崩溃现象的存在性及其成因进行定量研究，将对研究动量崩溃的风险管理手段具有重要的实践价值。另一方面，国内对于动量崩溃风险管理方法的探索，尤其对于中国商品期货市场，将极端市场环境下出现的动量崩溃风险单独提出，并且使用严谨定量方法进行深入研究且获得成熟理论成果的学者较少，进一步提出行之有效的风险管理方法和措施的学者相对更少。本文在研究中国商品期货市场动量效应存在性和动量策略有效性的同时，着重研究中国商品期货市场动量崩溃现象的存在性及其成因，基于在动量崩溃期动量收益的风险暴露，尝试对原始的动量策略进行优化以解决动量崩溃带来策略的极端损失问题，这对于广泛使用动量策略的基金经理的风险管理实操具有极强的研究意义。

本文的边际贡献在于：第一，在设定交易成本对中国商品期货市场动量策略进行验证的基础上，首次研究中国商品期货市场动量崩溃的存在性，发现中国商品期货市场动量崩溃现象与美国各类金融资产动量崩溃的相同与不同之处；第二，对中国商品期货市场发生动量崩溃的原因进行发掘，基于这一领域学者的前沿研究，首次对中国商品期货动量收益的时变β和类期权性质进行检验，认为其发生动量崩溃的原因是由于动量组合存在不对称的类期权性质；第三，针对动量崩溃的风险管理方法，首次提出构建基于目标条件停时的动态权重动量策略。一方面，基于组合管理思想推导动量组合的动态最优配置比例，据此最优比例设定动量策略的开仓权重，以实现夏普比例最大的最优化目标；另一方面，在动态权重动量策略的基础上，根据预测能力较强的风险因子，增加目标条件停时使得在风险超过所设定的阈值时暂停策略开仓，提高策略规避崩溃风险的能力，为CTA基金经理提供可行的风险管理方法。

1 文献综述

动量效应^[1]，是指金融资产的收益率在未来一段时间内会延续原来的运动方向，与之相对地，反转效应是指金融资产的收益率在未来一段时间内会呈现与历史相反的运动方向，二者的存在表明市场处于非有效的状态，动量策略和反转策略正是基于这一市场无效性而捕捉超额收益。

动量策略和反转策略被验证在各类资产中均有效。Jegadeesh和Titman^[1]、Conrad和Kaul^[5]、Grundy和Martin^[6]提出动量策略并报告在美国股市运用动量策略取得显著性收益，且验证了动量策略在美国股市中所有子时期都有效；Rouwenhorst^[7]、Chan等^[8]和Asness等^[9]分别使用欧洲股票市场、国际股票市场指数和其他大类资产对动量策略盈利效果进行验证，盈利结果在统计上也是显著的。相比之下，国内的研究起步较晚，研究方法与国外学者类似。王永宏和赵友军^[10]、周琳杰^[11]和钱春海^[12]基于沪深股票市场周度数据发现中国股票市场存在显著的反转效应，并且发现随着持有期的延长，动量组合的超额收益会呈现明显下降的趋势。吴志国和王相宁^[13]基于澳大利亚、法国等7个国家的外汇市场并加载短期和中期动量策略, 结果表明这些市场中短期均表现为动量效应，长期均表现为反转效应。

聚焦于动量策略在商品期货市场的验证与收益增强，国内外学者均有相关的研究。Miffre和Rallis^[14]将动量策略应用于商品期货市场，发现动量回报与传统资产的回报之间相关性很低，这使得以商品为基础的增强型投资组合成为分散化投资组合的理想选择。Shen等^[15]将动量策略运用于商品期货市场且同样具有显著的超额收益，并且得出结论动量策略的收益来源于行为金融因素，而非风险补偿。Fuertes等^[16]利用动量和期限结构信号的双重分类策略明显优于单一分类策略。Bianchi等^[17]在单排序动量策略的基础上，针对商品期货市场建立双重排序动量策略，并且盈利结果更加优于单排序策略。Chaves和Viswanathan^[18]研究商品期货价格的动量和均值回归策略及其与商品现货价格的动量和均值回归的关系，结果发现动量在期货市场中表现优于现货市场。王智力^[19]对中国商品期货市场加载动量策略，发现在短期内动量投资策略有效。李辰旭等^[20]基于2012年全部商品期货的数据，并在模型中加入汇率、利率等因子，获得更高的动量收益。

关于动量崩溃及其风险管理，国外学者的研究发端较早，并且已经形成了一系列成熟的研究成果。关于动量崩溃的驱动因素，学者们的观点不尽相同。Shanken和Kothari^[21]、Grundy和Martin^[6]研究发现动量组合尽管是同时做多和做空的市场中性策略，但其市场因子风险暴露β具有时变性，这种风险暴露β具有时变性在某些极端市场环境中给动量收益带来不利影响。Cooper等^[22]发现当市场处于熊市时，动量收益将会降低，甚至可能出现崩溃。Stivers和Sun^[23]认为当市场波动率水平较高时，动量组合将倾向于出现损失甚至崩溃。Daniel等^[24]、王小华等^[25]基于HMM模型来刻画历史收益率和当期收益率对于动量策略的影响，并得到在市场动荡期时，动量策略的极端损失更有倾向发生。Avramov等^[26]研究市场流动性降低将会给动量收益带来不利影响。Grobys^[27]调查发现动量崩溃与宏观经济衰退有关。Yan^[28]认为是拥挤交易造成了动量崩溃，通过只做空无拥挤的失败者可以避免横截面上的动量崩溃；Barroso和Santa-Clara^[29]认为动量崩溃发生是因为动量因子本身也有动量效应。

其次，国外学者对于动量崩溃的风险管理提出较多的方法。Han等^[30]面对极端的动量损失提出一种止损策略，当动量收益连续回撤到一定阈值就清仓止损。Barroso和Santa-Clara^[4]提出构建用动量收益的已实现波动率的倒数为权重的固定波动率动量策略进行风险管理；Heidari^[31]提出目标动量组合波动率停时的动量策略，即当动量组合波动率达到过去5年的80 % 分位数时就暂停开仓；Daniel和Moskowitz^[3]基于GJR-GARCH模型预测动量收益波动率，基于夏普比例最大化的条件估计下一期最优开仓比例建立动态权重动量策略；Dobrynskaya^[32]设定在市场崩溃后将原本的动量策略切换成相反的反向策略，并保持反向持仓3个月，然后恢复到正常的开仓状态的风险管理方法。国内学者对这一领域的研究较少。杨高飞等^[33]基于中国股票市场，通过构建风险因子对动量崩溃期的动量收益进行预测，依据风险因子的预测结果进而构造基于目标波动率停时的动量策略以规避动量崩溃的发生。

2 方法与模型 2.1 动量策略构建方法

本文采用Shen等^[15]和Bianchi等^[17]构建期货动量策略的方法。构建步骤如下：

首先，定义排序期J(J=1、2、3、4、6、8、12、26、52、104周)、持有期K(K=1、2、3、4、6、8、12、26、52、104周)和动量策略MOM(J-K)。对于第i个品种在当前时刻t，计算其在排序期j，即从第(t-j+1)周至第t周内的累积对数收益率

$ R_i(t-j+1, t)=\sum\limits_{k=t-j+1}^t R_l^i . $

(1)

其中: R_lⁱ表示第i个品种在第l周的收益率，R_i(t-j+1, t)表示第i个品种在排序期j内的累积收益率。

其次，根据计算出的所有品种在排序期J内的累积收益率进行排序，分别定义累积收益率最高的1/3为W组合、累积收益率最低的1/3为L组合，做多W组合并做空L组合得到动量组合MOM(J-K)，对组合里面的每个品种等权重开仓。

最后，将组合持有K周，月底进行移仓换月，计算持有期内的平均周度收益率。若动量组合MOM(J-K)在持有期的周度收益率显著大于零，则说明中国商品期货市场存在动量效应；反之，存在反转效应；而如果收益率不显著时，则说明中国商品期货市场不存在动量效应或反转效应。

本文编制策略时考虑交易费用，设定开平仓的交易费用率为0.01 %。目前，根据国内3大商品期货交易所公布的交易佣金规则，佣金分为固定金额和固定比例两种收取方式，固定金额佣金为1.5~10元/手，固定比例佣金为0.004 % ~0.015 %，此外，国内的商品期货交易所还需以0.002 % 的比例收取投资者保障基金，加上本文构建的策略需要进行移仓换月，因此本文设定交易费用率为0.01 %，可以更加合理地反映交易的真实情形。

2.2 商品期货动量组合的时变β与类期权性质

通过构建时变β以考察动量崩溃的成因，借鉴Daniel和Moskowitz^[3]使用前4周市场组合收益对动量组合时变β进行估计，如下

$ \begin{aligned} \tilde{R}_{{\mathrm{mom}}, t}=& \beta_0^{\mathrm {mom }} \tilde{R}_{{\mathrm{mkt}}, t}+\beta_1^{{\mathrm{mom}}} \tilde{R}_{{\mathrm{mkt}}, t-1}+\\ & \beta_2^{\mathrm {mom }} \tilde{R}_{{\mathrm{mkt}}, t-2}+\beta_3^{\mathrm {mom }} \tilde{R}_{{\mathrm{mkt}}, t-3}+\tilde{\varepsilon}_t. \end{aligned} $

(2)

其中：$\tilde{R}_{{\mathrm{mom}}, t}$表示第t周动量策略的超额收益，$\tilde{R}_{{\mathrm{mkt}}, t}$表示第t周市场组合溢价率。对参数进行拟合并将估计量$\hat{\beta}_t^{\mathrm{mom}}$=($\hat{\beta}_0^{\mathrm{mom}}$+$\hat{\beta}_1^{\mathrm{mom}}$+$\hat{\beta}_2^{\mathrm{mom}}$+$\hat{\beta}_3^{\mathrm{mom}}$)作为动量组合时变β的研究对象。同时，为了考察赢家组合和输家组合的时变β，使用如下回归进行拟合并估计其时变β。

$ \begin{aligned} \tilde{R}_{w, t}=& \beta_0^w \tilde{R}_{{\mathrm{mkt}}, t}+\beta_1^w \tilde{R}_{{\mathrm{mkt}}, t-1}+\beta_2^w \tilde{R}_{{\mathrm{mkt}}, t-2}+\\ & \beta_3^w \tilde{R}_{{\mathrm{mkt}}, t-3}+\tilde{\varepsilon}_t, \end{aligned} $

(3)

$ \begin{aligned} \tilde{R}_{l, t}=& \beta_0^l \tilde{R}_{{\mathrm{mkt}}, t}+\beta_1^l \tilde{R}_{{\mathrm{mkt}}, t-1}+\beta_2^l \tilde{R}_{{\mathrm{mkt}}, t-2}+\\ & \beta_3^l \tilde{R}_{{\mathrm{mkt}}, t-3}+\tilde{\varepsilon}_t . \end{aligned} $

(4)

其中：$\tilde{R}_{w, t}$表示第t周赢家组合W(J-K)的超额收益, $\tilde{R}_{l, t}$表示第t周输家组合L(J-K)的超额收益。赢家组合的估计量为$\hat{\beta}_t^w$=($\hat{\beta}_0^w$+$\hat{\beta}_1^w$+$\hat{\beta}_2^w$+$\hat{\beta}_3^w$)，输家组合的估计量为$\hat{\beta}_t^l$=($\hat{\beta}_0^l$+$\hat{\beta}_1^l$+$\hat{\beta}_2^l$+$\hat{\beta}_3^l$)。

其次，评估动量组合的上行市场和下行市场β的差异，在CAPM模型中加入熊市状态变量I_{B, t}、牛市状态变量I_{L, t}和市场组合收益率状态变量$\tilde{I}_{U, t}$，构建条件CAPM模型：

$ \begin{aligned} \tilde{R}_t=& {\left[\alpha_0+\alpha_B I_{B, t-1}\right]+\left[\beta_0+I_{B, t-1}\left(\beta_B+\right.\right.} \\ &\left.\left.\beta_{B, U} \tilde{I}_{U, t}\right)\right] \tilde{R}_{{\mathrm{mkt}}, t}+\tilde{\varepsilon}_t, \end{aligned} $

(5)

$ \begin{aligned} \tilde{R}_t=& {\left[\alpha_0+\alpha_L I_{L, t-1}\right]+\left[\beta_0+I_{L, t-1}\left(\beta_L+\right.\right.} \\ &\left.\left.\beta_{L, U} \tilde{I}_{U, t}\right)\right] \tilde{R}_{{\mathrm{mkt}} , t}+\tilde{\varepsilon}_t . \end{aligned} $

(6)

其中：$\tilde{R}_t$表示组合的超额收益，$\tilde{R}_t$可以为动量组合的超额收益($\tilde{R}_{{\mathrm{mom}}, t}$)，也可以为赢家组合的超额收益($\tilde{R}_{w, t}$)和输家组合的超额收益($\tilde{R}_{l, t}$)，表示动量策略的超额收益，$\tilde{R}_{{\mathrm{mkt}}, t}$表示市场组合的溢价率；I_{B, t}表示t时刻市场是否处于熊市状态，定义近1年市场组合累积收益为负即为熊市，I_{B, t}=1表示t时刻市场处于熊市，否则为0；I_{L, t}表示t时刻市场是否处于牛市状态，定义近1年市场组合累积收益为正即为牛市，I_{L, t}=1表示t时刻市场处于牛市，否则为0；$\tilde{I}_{U, t}$表示t时刻市场组合溢价是否为正，若$\tilde{I}_{U, t}$=1表示市场组合溢价为正，否则为0。如果β_{B, U}或者β_{L, U}显著，则表明市场拐点对动量组合收益具有显著影响，以致于有可能产生类期权性质。

2.3 基于风险因子预测动量崩溃

动量策略倾向于在当地市场暴跌后的1~3个月内崩溃，动量崩溃通常发生在市场快速下跌后的反弹过程中，此时的市场波动率通常处于较高水平^{[3, 29, 31-32]}。Barroso和Santa-Clara^[4]指出动量收益的波动率对动量崩溃有预测作用，Daniel和Moskowitz^[3]认为市场状态，即市场组合的波动率对动量崩溃有预测效果。另外，考虑动量崩溃发生时的市场状态和动量组合的类期权性质，本文选择6个风险因子用于动量崩溃的预测，包含4个市场组合状态因子和2个动量组合状态因子，分别是市场组合超额收益率($\tilde{R}_{{\mathrm{mkt}}, t}$)、市场组合收益率一阶差分(ΔR_mkt)、市场组合波动率(σ_mkt²)、市场组合波动率的一阶差分(Δσ_mkt²)、动量组合波动率(σ_mom²)和动量组合波动率的一阶差分(Δσ_mom²)。

1) 市场组合超额收益率($\tilde{R}_{{\mathrm{mkt}}, t}$)：选择南华商品综合指数的周度收盘价数据计算对数收益率，并减去对数无风险收益率得到风险溢价部分，作为商品期货市场的风险因子可以较好地描述国内整体商品期货市场的价格变化以及风险溢价水平。

$ \tilde{R}_{{\mathrm{mkt}}, t}=\ln \left({\mathrm{CFI}}_t\right)-\ln \left({\mathrm{CFI}}_{t-1}\right)-r_{f, t}. $

(7)

其中：CFI_t表示第t周南华商品综合指数的周度收盘价格, r_{f, t}表示第t周对数无风险收益率。

2) 市场组合收益率一阶差分(ΔR_mkt)：联系动量组合的类期权性质，该因子可以反映当前市场组合收益率变化的速度，即反映南华商品综合指数的二阶变化。

$ \Delta R_{{\mathrm{mkt}}, t}=R_{{\mathrm{mkt}}, t}-R_{{\mathrm{mkt}}, t-1} . $

(8)

其中：R_{mkt, t}表示第t周南华商品综合指数的周度对数收益率。

3) 市场组合波动率(σ_mkt²)：使用南华商品综合指数前20个交易日的日度对数收益率计算其方差，以反映当前市场的波动水平。

$ \sigma_{{\mathrm{mkt}}, t}^2=\frac{1}{20} \sum\limits_{j=1}^{20}\left(R_{{\mathrm{mkt}}, t-j}^{{\mathrm{daily}}}-\overline{R_{{\mathrm{mkt}}}^{\mathrm {daily }}}\right)^2. $

(9)

其中: R_{mkt, t}^daily表示t时刻南华商品综合指数的日度对数收益率，$\overline{R_{\mathrm{mkt}}^{\mathrm {daily }}}$表示南华商品综合指数前20个交易日的日度对数收益率的平均值。

4) 市场组合波动率的一阶差分(Δσ_mkt²)：该因子可以反映市场组合收益波动率变化的速度。

$ \Delta \sigma_{{\mathrm{mkt}}, t}^2=\sigma_{{\mathrm{mkt}}, t}^2-\sigma_{{\mathrm{mkt}}, t-1}^2. $

(10)

其中: σ_{mkt, t}²表示第t周南华商品综合指数前20个交易日的日度对数收益率的方差。

5) 动量组合波动率(σ²)：使用动量组合前4周动量收益计算其方差，以反映当前动量组合的收益波动水平。

$ \sigma_t^2=\frac{1}{4} \sum\limits_{j=1}^4\left(R_{{\rm {mom }}, t-j}-\overline{R_{\rm {mom }}}\right)^2 . $

(11)

其中: R_{mom, t}表示第t周的动量收益，$\overline{R_{\rm {mom }}}$在第t周时，动量组合前4周动量收益的均值。

6) 动量组合波动率的一阶差分(Δσ²)：该因子可以反映动量收益波动率变化的速度。

$ \Delta \sigma_t^2=\sigma_t^2-\sigma_{t-1}^2. $

(12)

其中: σ_t²表示第t周时，动量组合前4周动量收益的方差。

为检验以上风险因子的预测能力，在考虑因子之间的多重共线性之后，使用以下多元线性回归模型，并加入Fama-French三因子作为控制变量。

$ \begin{gathered} \tilde{R}_{{\mathrm{mom}}, t}=\alpha+\beta_{{\mathrm{MKT}}} {\mathrm{MKT}}_{t-1}+\beta_{{\mathrm{SMB}}} {\mathrm{SMB}}_{t-1}+ \\ \beta_{\mathrm {HML }} {\mathrm{HML}}_{t-1}+\beta_i X_{i, t-1}+\varepsilon_t, \\ i=1, 2, \cdots, 6. \end{gathered} $

(13)

其中: $\tilde{R}_{{\mathrm{mom}}, t}$表示第t周的动量收益相对于无风险利率的溢价，MKT_t、SMB_t和HML_t分别表示第t周的Fama-French市场因子、规模因子、价值因子，X_{i, t}表示第t周的风险因子。若β_i显著，则表明该风险因子具有一定的预测效果。

更进一步，考察动量奔溃期的因子预测。定义第t周动量收益低于-2.5 % 时即处于动量崩溃期，使用动量崩溃期子样本，基于回归模型(13)检验动量崩溃期各风险因子的预测效果。

2.4 构建基于目标条件停时的动态权重动量策略

针对动量崩溃的风险管理，在基础动量策略上构建基于目标条件停时的动态权重动量策略。基于Markowitz的“均值-方差模型”，考虑最简单的投资组合，即组合中仅包含动量组合和无风险资产，在t时刻配置权重分别为ω_t和(1-ω_t)。假设可以以无风险利率借入或借出无风险资产，同时在样本空间上，对于离散时间测度即周度T∈{1, 2, …, T}，在已知第t周的条件下，第t+1周动量策略超额收益$\tilde{R}_{{\mathrm{mom}}, t+1}$的条件期望服从正态分布，条件期望为$\tilde{\mu}_t$，条件方差为σ_t²，即

$ \begin{gathered} \tilde{\mu}_t=\mathbb{E}_t\left[\tilde{R}_{{\rm {mom }}, t+1}\right], \\ \sigma_t^2=\mathbb{E}_t\left[\left(\tilde{R}_{{\rm {mom }}, t+1}-\tilde{\mu}_t\right)^2\right], \\ t \in\{0, 1, \cdots, T-1\} . \end{gathered} $

(14)

那么，在已知第t周的条件下，第t+1周该组合的超额收益$\tilde{R}_{p, t+1}$的条件分布为

$ \begin{gathered} \tilde{R}_{p, t+1}=\omega_t \tilde{R}_{{\mathrm{mom}}, t+1} \sim \mathcal{N}\left(\omega_t \tilde{\mu}_t, \omega_t^2 \sigma_t^2\right), \\ t \in\{0, 1, \cdots, T-1\} . \end{gathered} $

(15)

那么，组合在全样本空间上的夏普比例为

$ S R=\frac{\mathbb{E}\left[\frac{1}{T} \sum\limits_{t=1}^T \tilde{R}_{p, t}\right]}{\sqrt{\mathbb{E}\left[\frac{1}{T} \sum\limits_{t=1}^T\left(\tilde{R}_{p, t}-\overline {{{\tilde R}_p}} \right)^2\right]}} . $

(16)

其中: $\overline {{{\tilde R}_p}}$是样本空间上，组合超额收益率的均值。于是，最优化目标为实现组合在全样本空间上夏普比例的最大化，即

$ \max\limits _{\omega_0, \omega_1, \cdots, \omega_{T-1}} \mathbb{E}\left[\frac{1}{T} \sum\limits_{t=1}^T \tilde{R}_{p, t}\right], \\ {\rm{s. t.}}\; \mathbb{E}\left[\frac{1}{T} \sum\limits_{t=1}^T\left(\tilde{R}_{p, t}-\overline{\tilde{R}_p}\right)^2\right]=\sigma_p^2. $

(17)

当时间周期较短时，有

$ \begin{aligned} \mathbb{E}\left[\left(\tilde{R}_{p, t}-\overline{\tilde{R}_p}\right)^2\right] & \approx \omega_t^2 \sigma_t^2 \\ &=\omega_t^2 \mathbb{E}_t\left[\left(\tilde{R}_{{\rm {mom }}, t+1}-\tilde{\mu}_t\right)^2\right] . \end{aligned} $

(18)

基于此构建拉格朗日方程

$ \begin{array}{l} \max \limits_{\omega_0, \omega_1, \cdots, \omega_{T-1}} \mathcal{L} \equiv \max \limits_{\omega_t}\left(\frac{1}{T} \sum\limits_{t=0}^{T-1} \omega_t \tilde{\mu}_t\right)- \\ \lambda\left(\frac{1}{T} \sum\limits_{t=0}^{T-1} \omega_t^2 \sigma_t^2=\sigma_p^2\right). \end{array} $

(19)

λ为拉格朗日乘子。对式(19)求导并令其等于0, 得

$ \begin{gathered} \left.\frac{\partial \mathcal{L}}{\partial \omega_t}\right|_{\omega_t=\omega_t{ }^*}=\frac{1}{T}\left(\tilde{\mu}_t-2 \lambda \omega_t{ }^* \sigma_t^2\right)=0, \\ t \in\{0, 1, \cdots, T-1\} . \end{gathered} $

(20)

令式(20)等于0, 得到最优动量组合配置权重

$ \omega_t^*=\left(\frac{1}{2 \lambda}\right) \frac{\tilde{\mu}_t}{\sigma_t^2} \text {. } $

(21)

从式(21)可以看到，在时刻t动量组合的配置权重与条件期望$\tilde{\mu}_t$成正比，与条件方差σ_t²成反比。通过对第t+1周条件期望与条件方差分别进行估计，得到${{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\tilde{\mu }}}}_{t+1}}$和${\hat{\sigma }_{t+1}^{2}}$，以实现对第t+1周动量组合最优配置比例的估计$\hat{\omega }_{t+1}^{*}$，即

$ \hat{\omega }_{t+1}^{*}=\left( \frac{1}{2\lambda } \right)\frac{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\tilde{\mu }}}}_{t+1}}}{\hat{\sigma }_{t+1}^{2}}, t\in \{0, 1, \cdots , T-1\}. $

(22)

参考Daniel和Moskowitz^[3]的方法，若动量组合具有类期权效应，那么在相应的市场环境下其期权的价值与市场组合的波动率相关，在一定程度上其收益率可以通过市场组合波动率进行预测，即估计量${{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\tilde{\mu }}}}_{t+1}}$由如下回归模型进行预测：

$ \begin{aligned} \tilde{R}_{{\mathrm{mom}}, t}=& \gamma_0+\gamma_1 \cdot I_{B, t-1}+\gamma_2 \cdot \sigma_{{\mathrm{mkt}}, t-1}^2+\\ & \gamma_3 \cdot I_{B, t-1} \cdot \sigma_{{\mathrm{mkt}}, t-1}^2+\tilde{\varepsilon}_t. \end{aligned} $

(23)

其中: I_{B, t-1}表示滞后一期的熊市状态因子，其定义与前文一致；σ_{mkt, t-1}²表示滞后一期的市场组合波动率。

另一方面，估计量$\hat \sigma _{t + 1}^2$由GJR-GARCH预测的动量收益序列波动率和过去26周动量收益波动率进行线性估计。首先建立动量收益序列的GJR-GARCH拟合模型^[34]，GJR-GARCH模型可以更好地拟合市场波动的动态结构。模型假设动量组合MOM(J-K)在t时刻的收益率R_{mom, t}服从随机过程

$ R_{{\mathrm{mom}}, t}=\mu+\varepsilon_t. $

(24)

其中：ε_t~N(0, σ_{GARCH, t}²)，收益率序列的波动率σ_{GARCH, t}²服从回归

$ \begin{aligned} \sigma_{{\mathrm{GARCH}}, t}^2=& \omega+\beta \sigma_{{\mathrm{GARCH}}, t-1}^2+\\ &\left(\alpha+\gamma I_{\left(\varepsilon_{t-1}<0\right)}\right) \varepsilon_{t-1}^2. \end{aligned} $

(25)

其中：I_{(εt-1 < 0)}为示性变量，当ε_t-1 < 0时取1，否则为0。使用极大似然估计对参数进行估计，并对样本空间上的条件方差进行拟合。

其次，根据线性回归模型(26)分别对GJR-GARCH模型和滞后一阶的动量组合波动率对动量组合波动率的预测效果进行检验：

$ \sigma_{t+1}=\alpha+\beta_{{\mathrm{VOL}}} \cdot \sigma_t+\beta_{{\mathrm{GARCH}}} \cdot \sigma_{{\mathrm{GARCH}}, t} \cdot $

(26)

使用预测效果较好的模型预测估计量$\hat \sigma _{t + 1}^2$并进一步计算得到第t+1周动量组合的最优配置比例。

在构建出的动态权重动量策略的基础上，根据预测模型(13)挑选出效果最好的风险因子，进一步构建基于目标条件停时的动态权重动量策略，即设定一个风险因子的目标区间，当风险因子处于目标区间内则开仓进行动态权重动量策略，而达到目标区间以外的极端范围时则在下期暂停开仓，模型设定为

$ \left\{\begin{array}{c} \omega_{t+1}=\omega_{t+1}^*, X_{i, t} \in F_i, \\ \omega_{t+1}=0, X_{i, t} \notin F_i, \end{array}\right.\\i=1, 2, \cdots, 6, t=0, 1, \cdots, T-1 . $

(27)

其中：ω_t表示第t周动量组合的开仓权重，X_{i, t}表示第i个风险因子，F_i表示第i个风险因子的目标区间。

3 实证分析 3.1 样本数据

采用国内商品期货市场周度频率数据作为研究对象，样本区间是2005年1月7日—2020年2月7日，数据来自于国泰君安数据库和Wind资讯。在品种与市场收益率方面，选取2013年之前上市、交易量较活跃的25个商品期货品种，表 1列举了所选取的各个品种与南华期货商品指数的名称、品种代码、数据开始日期以及描述性统计。与股票市场不同，期货合约具有到期日，通常该品种的近月合约交易最为活跃，因此，将所有品种均取合约交割月份上一个月的周度收盘价合成连续合约，采用所合成的连续合约价格计算周度对数收益率。同时对于期货市场，采用南华综合指数作为市场组合，并计算周度对数收益率。

3.2 动量效应验证与动量策略收益结果

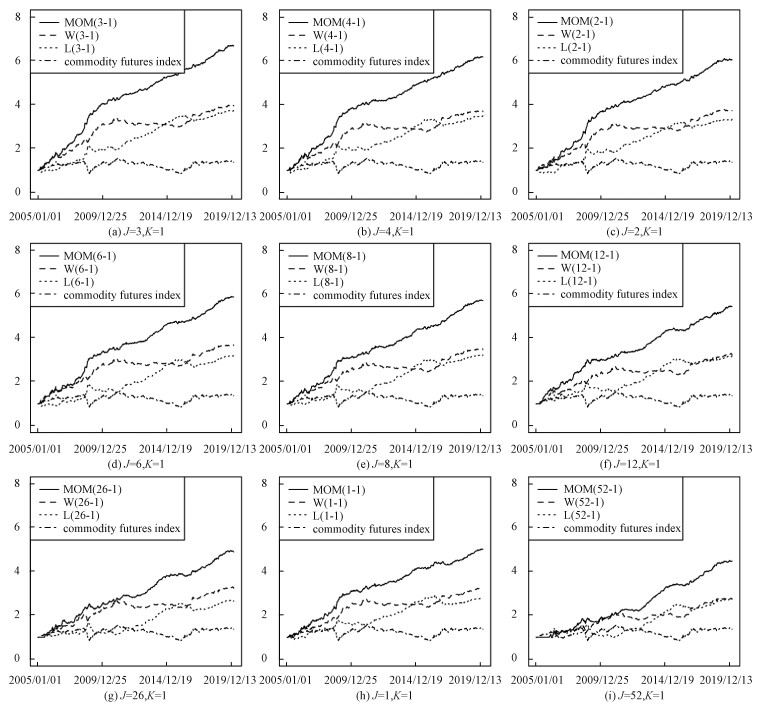
选取排序期J和持有期K分别为1、2、3、4、6、8、12、26、52、104周，共形成100种投资组合，附录一整理了收益表现较好的动量策略MOM(J-K)、仅做多赢家组合(W)和仅做空输家组合(L)的平均周度收益结果，同时图 1展示了部分策略的累积净值曲线。观察数据结果，由于考虑交易成本，因此在5 % 的显著性水平下，本文测试的100种动量策略中有29种具有显著大于零的周平均收益，且收益表现远远优于南华商品综合指数，表明在周度频率上，中国商品期货市场存在显著的动量效应，策略的净值曲线呈现较为平稳的走势(见图 1)。其中，动量组合MOM(3-1)的周平均收益率和夏普比率均最高，分别达到0.72 % 和0.31。在收益显著大于零的动量组合当中，MOM(1-3)的周平均收益率和夏普比率均最低，分别为0.14 % 和0.07，详细收益指标见附录1。对比近10年上证指数的周度夏普比率为0.001 4，表明在中国商品期货市场使用动量策略可以取得较好的风险调整回报。

策略在不同子样本上均有效，且不存在季节效应的影响。商品期货综合指数可以反映商品期货市场整体的波动情况，当商品期货指数波动率较高时，表明当前金融市场波动幅度较大，根据南华商品商品综合指数波动水平的高低，将样本均分成5个子样本进行稳健性测试，子样本的样本区间分别为2005年7月1日—2008年1月4日的市场低波动区间、2008年1月4日—2012年1月6日的市场高波动区间、2012年1月6日—2015年1月2日的市场低波动区间、2015年1月2日—2018年1月5日的市场高波动区间、2018年1月5日—2020年2月7日的市场低波动区间，使用相同的策略构建方法分别加载动量策略，对策略进行稳健性测试，测试的详细结果见附录2。结果显示动量策略在各个样本上均能获得显著的风险调整收益，表明金融市场无论是处于高波动状态还是低波动状态，动量策略均是有效的。另一方面，检验策略是否存在季节效应，将25个商品期货品种按照农产品类、金属类、化工类、能源类和建材类5大类进行归类，参考Bianchi^[17]的方法，依次去除其中某一品类并加载动量策略。测试的详细结果见附录2，全样本中表现出显著收益的动量组合在各个子样本中依然实现显著的收益，收益结果与全样本的收益结果保持较高的一致，因此，动量策略的收益不受季节效应的影响。

3.3 动量崩溃的发生与成因

尽管动量策略可以带来显著的收益和优秀的夏普比例，但是在极端的市场环境中还是会出现“崩溃”现象^[25]。动量崩溃所带来的便是当期的极端的负收益，使得累积收益产生较大的回撤。以收益表现最好的MOM(3-1)为例，该组合在样本空间上发生动量崩溃的次数达到40次，且在样本空间上出现2次单周损失超过7 %，不少组合存在单周损失超过8 % 的情形。

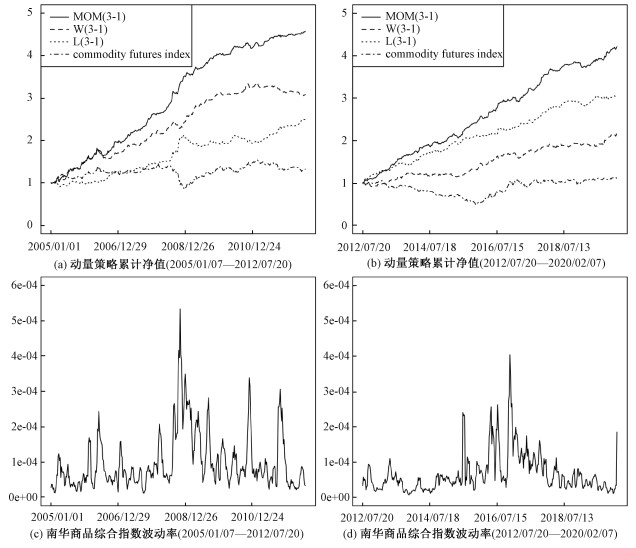
根据表 2的统计数据，对于29种具有显著动量收益的组合中，存在5种组合收益率序列5 % 分位点低于-2.5 %，存在25种组合最大回撤超过15 %，且主要集中于夏普比例较高的策略组合。以动量组合MOM(3-1)对为例，图 2展示了动量组合MOM(3-1)、赢家组合W(3-1)、输家组合L(3-1)和市场组合(南华商品综合指数)的净值走势，同时展示同期市场组合波动率的走势。分析动量组合MOM(3-1)历次崩溃的情形，当动量崩溃发生时，市场环境往往存在两种情形：一是市场组合波动率较高且市场组合下行后快速反弹过程，二是市场组合波动率较高且市场组合上行后快速下跌过程。总之，商品期货动量策略存在动量崩溃现象，并且崩溃往往出现在市场组合波动率较高且市场组合走势出现拐点的时候。

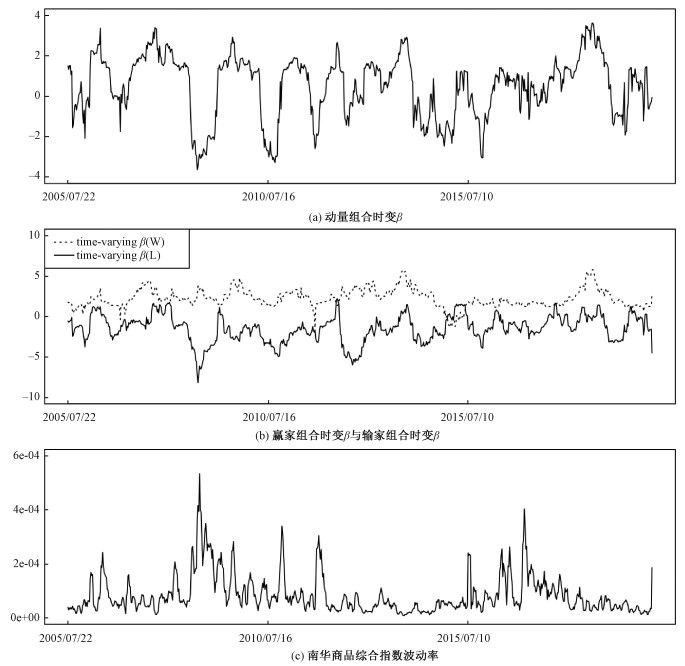
导致动量崩溃的原因是什么？首先，通过回归(2)~回归(4)将前26周动量组合收益滚动回归得到动量组合MOM(3-1)、赢家组合W(3-1)、输家组合L(3-1)的时变β(如图 3所示)。从图 3(a)来看，尽管长期来看动量组合的β敞口维持在零附近，但是短期内时变β可能出现较大的波动，尤其输家组合的时变β波动较大，而赢家组合的时变β波动相对较小。根据前文所观察的出现崩溃的两种情形以及图 3(b)的展示，一是当市场长期下行且快速反弹时，伴随着市场组合波动率的上升，输家组合的时变β快速下降，且幅度往往大于同期赢家组合时变β的上升幅度，导致动量组合MOM(3-1)的时变β在短期内出现大幅下降至极端负值，以致在市场反弹期仍出现大幅损失；相对应地，当市场长期上涨且快速下跌时，输家组合的时变β快速上升，且幅度往往大于同期赢家组合时变β的下降幅度，导致动量组合MOM(3-1)在快速下行的市场环境下短期内仍存在正的时变β，从而导致市场拐点后动量组合收益出现回撤。总之，输家组合时变β波动更大，对市场组合波动率更为敏感，主导动量组合在市场拐点时的时变β，从而导致市场拐点往往发生动量崩溃。

再者，考察动量策略的类期权效应。根据模型(5)和模型(6)对动量组合收益结果进行回归，回归结果在表 3中展示。对于动量组合的回归(5)和回归(6)的拟合结果，参数估计值${\hat \beta _{B, U}}$在5 % 的显著性水平下显著，表明市场下行后反弹期间这样的特殊市场环境中，市场组合收益对动量收益具有显著影响，且动量组合呈现类期权性质。具体而言，由于参数估计值${\hat \beta _{B, U}}$显著为负，当市场处于熊市时且当市场继续下行时，此时动量组合的条件β为-0.098 7(${\hat \beta _0}$+${\hat \beta _B}$)，动量组合随着市场组合的下跌将呈现收益，而如果市场在熊市里出现快速反弹时，此时动量组合的条件β将显著减少为-0.453 6(${\hat \beta _0}$+${\hat \beta _B}$+${\hat \beta _{B, U}}$)，容易在反弹中因为有显著为负的市场因子敞口而导致损失，这与前文的分析保持一致。因此在熊市，动量组合的头寸类似卖出看涨期权的头寸，具有类期权性质。接着分析动量组合在牛市是否具有类期权性质。当市场处于牛市当中，参数估计值${\hat \beta _{L, U}}$在5 % 的显著性水平下显著为正数，此时动量组合的条件β为0.211 8(${\hat \beta _0}$+${\hat \beta _L}$)，可以在牛市中获得正收益。而当牛市中市场进一步快速上涨时，参数估计值${\hat \beta _{L, U}}$并不显著，而且此时动量组合的条件β为0.307 1并依然保持正数，随着市场的进一步上涨而继续获取收益，此时的动量组合不具有类期权性质。总之，对于分别在熊市和牛市中的动量组合，其具有不对称的类期权性质。

进一步分析发现，输家组合呈现非对称的类期权性质并且主导动量组合的类期权性质，而赢家组合在熊市和牛市中均不具有类期权性质。使用赢家组合和输家组合的收益率序列，仍然基于模型(5)和模型(6)的条件CAPM模型进行分析。首先，对于赢家组合的条件CAPM拟合结果，参数估计值${\hat \beta _{B, U}}$和${\hat \beta _{L, U}}$均不显著，表明在市场下行后出现拐点并未对赢家组合的β造成显著影响。其次，对于输家组合的条件CAPM拟合结果，参数估计值${\hat \beta _{B, U}}$和${\hat \beta _{L, U}}$均显著，具体而言，参数估计值${\hat \beta _{B, U}}$在1 % 的显著性水平下显著，意味着当市场处于熊市中的反弹期时，做空输家组合的条件β将为-0.537 8(${\hat \beta _0}$+${\hat \beta _B}$+${\hat \beta _{B, U}}$)，显著为负的条件β将导致输家组合在此市场环境下出现亏损；参数估计值${\hat \beta _{B, U}}$在5 % 的显著性水平下显著，意味着当市场处于牛市中的加速上涨过程中，输家组合的条件β将显著提升至-0.009 5 (${\hat \beta _0}$+${\hat \beta _B}$+${\hat \beta _{L, U}}$)，但仍为负数，同样容易导致输家组合在市场上涨期出现损失，因此，此时的参数尽管依然显著但仍无法改变条件β为负的情形，从这一角度出发可以认为输家组合在牛市环境中不存在类期权性质。

鉴于以上的实证分析，可以发现动量组合非对称的类期权性质完全由输家组合主导。由于输家组合具有类期权性质而赢家组合不具有显著的类期权性质，因此输家组合的收益率包含这一期权的收益，从而相比较于赢家组合，输家组合收益对市场组合波动率的变化更加敏感。

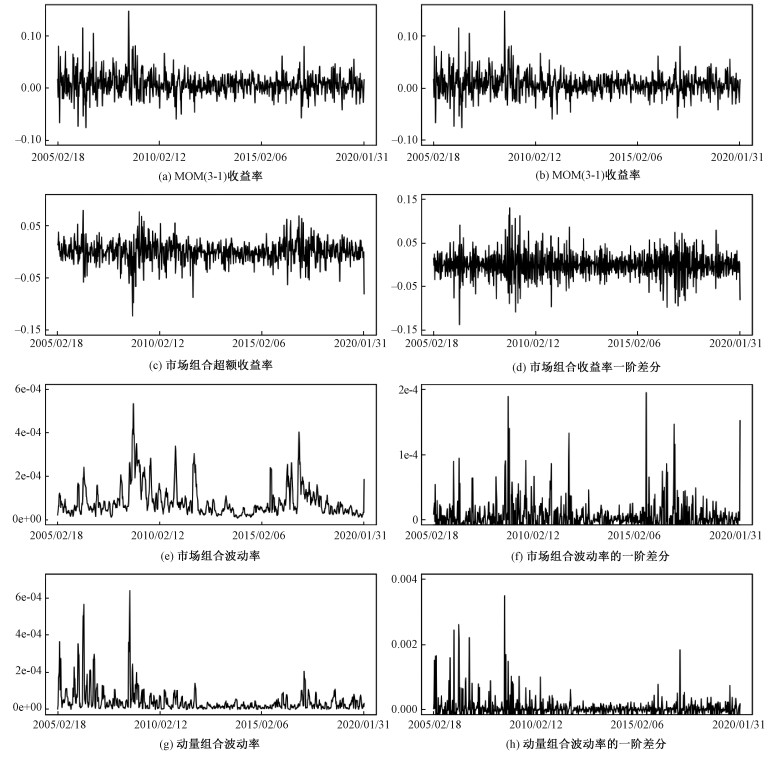
3.4 动量崩溃的预测

通过构建风险因子对动量崩溃进行预测。根据前文的描述，结合动量组合MOM(3-1)的收益结果，构建市场组合超额收益率(${\tilde R_{{\rm{mkt}}}}$)、市场组合收益率一阶差分(ΔR_mkt)、市场组合波动率(σ_mkt²)、市场组合波动率的一阶差分(Δσ_mkt²)、动量组合波动率(σ_mom²)和动量组合波动率的一阶差分(Δσ_mom²)这6个风险因子。图 4展示了动量收益与风险因子的变化趋势，定性来看，动量组合极端收益发生于市场剧烈波动中，同时伴随着市场组合波动率的大幅变化和动量收益自身波动率的快速变化。考察这6个风险因子的相关系数矩阵，除市场组合超额收益率与市场组合收益率一阶差分相关系数较高外，其他风险因子之间的相关性较低，考虑到动量组合具有类期权性质，市场组合超额收益率与市场组合收益率一阶差分都应当被考虑，总体来看，回归模型不具有多重共线性。

根据回归模型(13)，在全样本空间上考虑风险因子的预测效果，结果在附录3中进行展示。回归结果显示，在5 % 的显著性水平下，截距项和控制变量Fama-French市场因子的参数显著，但风险因子的回归参数均不显著，模型总体的预测能力较低，表明在全样本空间上风险因子对动量收益的预测能力较弱。接着，根据前文定义当周损失超过2.5 % 为动量崩溃期，基于模型(13)给出风险因子在动量崩溃期的拟合结果。在动量崩溃期，回归结果(如表 4所示)显示单个风险因子对动量崩溃的预测能力较弱，在5 % 的显著性水平下参数估计均不显著，但是同时使用市场组合收益率一阶差分和动量组合波动率对动量崩溃期动量组合收益率进行拟合，在5 % 的显著性水平下这2个风险因子的参数是显著的，联合使用市场组合收益率一阶差分和动量组合波动率这2个风险因子能够对动量崩溃起到较好的预测作用。

3.5 构建基于目标条件停时的动态权重动量策略

对于动量崩溃的风险管理，提出基于能够有效预测动量崩溃的风险因子及其组合来构建基于目标条件停时的动态权重动量策略。

第1步先估计理论最优配置权重ω_t+1^*，其估计过程和拟合效果在附录4中展示。第2步基于风险因子的预测效果构建基于目标条件停时的动态权重动量策略。Heidari^[32]以动量组合波动率过去60个月的80 % 分位数为阈值，杨高飞等^[34]以动量组合波动率过去10周的95 % 分位数为阈值。考虑到样本区间和数据频率，因此本文设定市场组合收益率一阶差分和动量组合波动率这2个风险因子的异常值为52周内95 % 的分位数，若当期因子超过这一异常值时，下一期则暂停开仓，直至当期风险因子回归正常区间后继续开仓，这样既可以有效规避异常值以减少动量损失，同时暂停开仓能够节约交易费用。据此，本文将目标条件设定为：

$ \left\{\begin{array}{c} \omega_{t+1}=\omega_{t+1}^*, \Delta R_{{\mathrm{mkt}}, t} \leqslant\left(\Delta R_{{\mathrm{mkt}}, t}\right)^{95 \%} \mid \sigma_{{\mathrm{mom}}, t}^2 \\ \leqslant\left(\sigma_{{\mathrm{mom}}}^2\right)^{95 \%}, \\ \omega_{t+1}=0, \Delta R_{{\mathrm{mkt}}, t}>\left(\Delta R_{{\mathrm{mkt}}, t}\right)^{95 \%} \mid \sigma_{{\mathrm{mom}}, t}^2 \\ >\left(\sigma_{{\mathrm{mom}}}^2\right)^{95 \%}, \end{array}\right.\\i=1, 2, \cdots, 6, t=0, 1, \cdots, T-1. $

(28)

基于以上2个步骤建立基于目标条件停时的动态权重动量策略。本文从夏普比例和平均周度收益率两个尺度去衡量策略收益的优化效果，并且另一方面基于尾部风险指标重点考察优化后策略是否有效地降低了动量崩溃带来的风险。

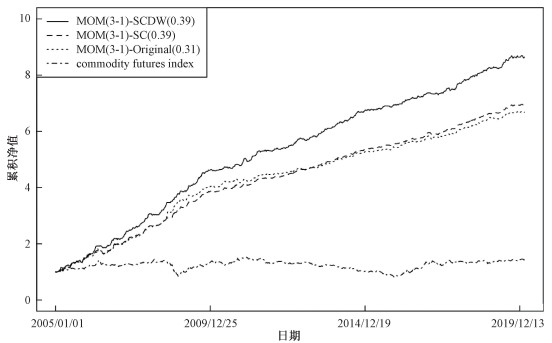
一方面，相比原始动量策略MOM(3-1)，基于目标条件停时的动态权重动量策略MOM(3-1)-SCDW可以大幅提升夏普比例和平均周度收益率。首先，对比原始动量策略和基于目标条件停时的动态权重动量策略，可以发现不论是夏普比例还是平均周度收益率，基于目标条件停时的动态权重动量策略均有所提升(见表 5)，具体而言，夏普比例从0.31提升至0.39，平均周度收益率从0.72 % 提升至0.98 %。其次，对比基于目标停时的动量策略和基于目标条件停时的动态权重动量策略，可以发现基于目标条件停时的动态权重动量策略MOM(3-1)-SCDW的夏普比例并未出现显著提升(仅提升0.001 8)，但平均周度收益率却显著提升，从0.76 % 提升至0.98 % (见图 5)。

另一方面，相比原始动量策略MOM(3-1)，基于目标条件停时的动态权重动量策略MOM(3-1)-SCDW可以有效改善动量崩溃风险。关注到收益率序列尾部风险的相关指标(见表 5)，单周最大损失从-7.60 % 改善至-6.18 %，策略最大回撤从-18.91 % 改善至-11.60 %，单周最大损失超过2.5 % 的周数从40降低至35，单周最大损失超过5 % 的周数从6降低至5，单周最大损失超过6 % 的周数从3降低至1，单周最大损失超过7 % 的周数从2直接降低至0，并且原始策略发生动量崩溃所对应的时期其收益大部分得到改善。

综上所述，对动量策略MOM(3-1)而言，构建基于目标条件停时的动态权重动量策略MOM(3-1)-SCDW的方法既能提升夏普比例和平均周度收益率，又能作为动量崩溃风险管理的有效工具。

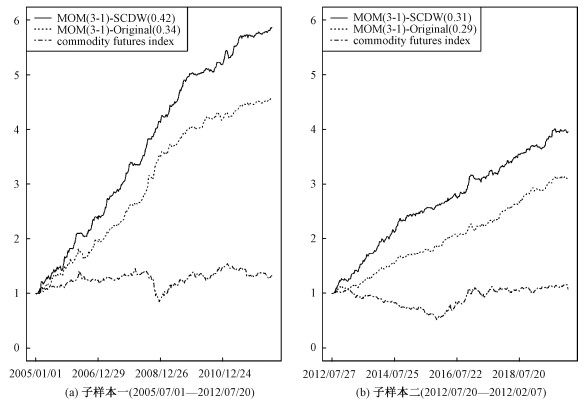
3.6 稳健性测试与样本外检验

首先对基于目标条件停时的动态权重动量策略进行稳健性测试。将动量策略MOM(3-1)的样本空间均分成两个子样本，在子样本区间上重复上一节的构建方法构建基于目标条件停时的动态权重动量策略。观察各个子样本上的收益结果(见图 6)，不论是对与收益能力的提升还是动量崩溃风险的管理，基于目标条件停时的动态权重动量策略均有效且保持稳健性。括号中数字为该策略的周度夏普比例，累积净值的初始净值为1元

使用另外8个收益较好的动量组合进行样本外检验。具体而言，针对每一个动量组合，重复风险因子回归和动态权重寻找的方法步骤，再构建8个所对应的基于目标条件停时的动态权重动量策略，基于目标条件停时的动态权重动量策略样本外检验收益结果在附录5中展示。首先对于收益提升能力，样本外的8个组合均实现平均周度和夏普比例的提升；其次，就动量崩溃风险管理能力而言，7个组合单周最大损失出现改善，6个组合历史最高回撤出现改善，大部分组合极端损失发生的频率出现改善。所以总体而言，在样本外的检验过程中，基于目标条件停时的动态权重动量策略能够对动量崩溃风险的管理起到积极的效果。

4 总结

以中国商品期货市场为实证对象，系统地分析了动量策略的有效性、动量崩溃的存在动因，并提出有效的动量崩溃风险管理方法，即构建基于目标条件停时的动态权重动量策略，有效地规避了动量崩溃带来的极端损失，同时获得了更好的平均周度收益和夏普比例。

动量因子作为配置最为广泛的因子之一，在考虑交易费用的情况下，仍能获得显著的风险调整收益。通过稳健型测试和季节效应测试，得出动量策略在各个子样本上均有效，且不存在季节效应的干扰，具有持续盈利的能力。实证发现中国商品期货市场存在动量崩溃现象，通过构建动量组合时变β和条件CAPM模型验证得到，输家组合的时变β波动较大并且主导动量组合时变β的变化，每当动量崩溃期输家组合的时变β快速变化并且主导动量组合时变β朝不利的方向发展，出现这样的现象是由于输家组合具有显著且不对称的类期权性质，进而使得输家组合对市场波动率等因子的变化更加敏感。

就对动量崩溃进行风险管理而言，通过构建基于目标条件停时的动态权重动量策略，有效地规避了动量奔溃带来的极端风险，同时获得更高的平均周度收益和夏普比例。一方面，基于组合管理思想，根据夏普比例最大化对理论最优配置比例进行最优化求解，通过波动率回归和GJR-GARCH模型对条件均值和条件方差进行估计，从而获取下一期理论最优开仓比例的估计值；另一方面，构建了6个风险因子，通过建立多因子模型筛选能够在动量崩溃期较好预测动量收益的风险因子，进一步设定开仓停时条件。最终结合以上两个方面构建基于目标条件停时的动态权重动量策略，该策略不仅将动量组合MOM(3-1)的夏普比例由0.31提升至0.39，而且显著降低了原始策略的最大单周损失、最大历史回撤以及发生极端损失的频率。经过稳健型测试和样本外检验，发现基于目标条件停时的动态权重动量策略具有良好的稳健型和普适性。

附录 1 动量策略收益部分结果 2 动量策略稳健型测试与季节效应测试详细结果
3 风险因子在全样本上的回归结果 4 动量策略最优配置权重$\hat \omega _{t + 1}^*$的详细估计过程

根据式(21)，在已知第t周的条件下，通过预期第t+1周条件期望与条件方差的比值来调整动量组合的配置比例$\hat \omega _{t + 1}^*$。而$\hat \omega _{t + 1}^*$的估计需要先对条件期望和条件方差分别进行预测得到${\widehat {\tilde \mu }_{t + 1}}$和$\hat \sigma _{t + 1}^2$。

一方面，基于模型(23)对条件期望${\widehat {\tilde \mu }_{t + 1}}$进行预测，回归模型拟合结果如附表 5所示。结果显示，回归(23-5)的参数估计值在5 % 的显著性水平下均显著，模型的预测能力最强，本文选用回归(23-5)对条件期望${\widehat {\tilde \mu }_{t + 1}}$进行预测并代入算法程序中。

另一方面，基于GJR-GARCH模型和模型(26)对条件期望$\hat \sigma _{t + 1}^2$进行预测。首先使用极大似然估计方法对GJR-GARCH模型进行拟合，拟合结果如附表 6所示。对于全样本的拟合结果，所有参数均在1 % 的显著性水平下显著，模型取得较好的拟合效果。并且模型在各个子样本上也取得较好的拟合效果，与全样本相比参数估计值变化差异不大，模型表现相对稳健。因此，使用GJR-GARCH模型能够较好地拟合动量组合收益率序列的波动特征。

其次，基于回归模型(26)获取条件方差的预测值。在全样本及其各个子样本上检验GJR-GARCH模型预测值和滞后一阶动量组合波动率对条件方差的预测效果，拟合结果见附表 7。回归结果显示，在全样本上GJR-GARCH模型预测值和滞后一阶动量组合波动率对条件方差具有较强的预测效果，同时在两个子样本上加载回归模型检验其预测能力的稳健性。在两个子样本上加载回归模型检验其预测能力的稳健性。结果显示在各子样本上，除部分截距项外，其他参数在1 % 的显著性水平下均保持显著，并且估计值未发生大幅变动，模型的R²也同样处于较高水平，模型的F检验均能通过。

5 基于目标条件停时的动态权重动量策略样本外检验详细收益结果

使用另外8个收益较好的动量组合进行样本外检验，且MOM(4-1)、MOM(2-1)、MOM(6-1)和MOM(8-1)样本外检验的详细收益结果与极端风险指标如附表 8所示。

另外4个组合，即MOM(12-1)、MOM(26-1)、MOM(1-1)和MOM(52-1)样本外检验的详细收益结果与极端风险指标如附表 9所示。