2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
合成孔径雷达(synthetic aperture radar,SAR)是一种全天时、全天候的成像雷达。动目标检测和测速是SAR领域的一个重要分支[1-5]。
传统的动目标测速方法是顺轨干涉测量(along track interferometry,ATI)[6-7],通过计算两幅图像的干涉相位估计动目标的速度,但是由于相位噪声等因素的影响,适用于测速精度要求不高的场景。
时频分析方法是分析线性调频信号的一种重要手段,因性能优越得到广泛应用。Yu和Zhang[8]利用分数阶傅里叶变换(fractional Fourier transform,FrFT)进行SAR成像,通过将参数搜索转换为一维优化问题来降低时间复杂度。Sun等[9]利用FrFT进行动目标检测,并通过CLEAN技术反复检测出强运动目标和弱运动目标。Chiu[10-11]将FrFT和ATI结合,可以在距离压缩后的数据域进行动目标测速和定位,但是没有对参数搜索问题进行优化。Zhang等[12]利用Radon-Wigner变换在时频平面的几何信息对线性调频信号进行参数估计。
通常FrFT求解最优值的方法是二维搜索,即遍历每个旋转角度计算FrFT,在角度-分数频率的二维平面内进行峰值搜索,得到最优旋转角度和能量聚焦的分数频率。但是,二维搜索的计算量很大,该方法需要在搜索间隔和搜索精度之间权衡。
本文通过分析线性调频信号的时频长度和FrFT投影长度之间的几何关系,提出一种新的动目标测速和定位方法。首先计算2个不同旋转角度下的FrFT投影长度,然后利用时频平面内的几何关系估计动目标信号的最优旋转角,最后利用最优旋转角进行FrFT计算,进一步对动目标测速和定位。利用3次FrFT运算可以大大缩短动目标参数估计的时间。
为进一步提高动目标参数估计的精度,针对静止信号进行去调频处理得到单频信号。利用单频信号在2个对称角度下的FrFT投影长度相等的特点,二者相减进行杂波抑制,有利于提高动目标的信杂比和参数估计精度。
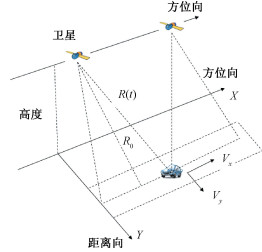
1 SAR动目标测速基础 1.1 动目标信号建模典型的SAR-GMTI几何示意图如图 1所示。
|
Download:
|
| 图 1 SAR-GMTI几何示意图 Fig. 1 Geometry diagram of SAR-GMTI | |
假设在方位向时间t=0时,雷达平台的位置是(0, 0, H),动目标的位置是(X, Y, 0)。雷达平台的速度是va。动目标的距离向速度是vy,方位向速度vx。
动目标和雷达平台之间的瞬时距离R随方位时间的变化,可以表示为
| $ \begin{gathered} R(t)=\sqrt{\left(X+v_x t-v_a t\right)^2+\left(Y+v_y t\right)^2+H^2} \approx \\ R_0+\frac{\left(v_x-v_a\right) X+v_y Y}{R_0}\left(t-t_0\right)+ \\ \frac{\left(v_a-v_x\right)^2+v_y^2}{2 R_0}\left(t-t_0\right)^2 . \end{gathered} $ | (1) |
其中:R0是初始时刻动目标和雷达平台之间的距离。t0是动目标的雷达波束中心穿越时刻,可以表示为
| $ t_0=\frac{x_0}{v_a-v_x}. $ | (2) |
动目标回波信号可以表示为
| $ \begin{gathered} s(t)=\sigma \cdot \operatorname{rect}\left(\frac{\tau-\frac{2 R(t)}{c}}{T_p}\right) \exp \left(\mathrm{j} {\rm{ \mathit{π} }} k_r\left(\tau-\frac{2 R(t)}{c}\right)^2\right) . \\ \operatorname{rect}\left(\frac{t}{T_a}\right) \exp \left(-\mathrm{j} \frac{4 {\rm{ \mathit{π} }} R_0}{\lambda}+2 \mathrm{j} {\rm{ \mathit{π} }} f\left(t-t_0\right)+\mathrm{j} {\rm{ \mathit{π} }} k_a\left(t-t_0\right)^2\right), \\ \left|t-t_0\right| \leqslant \frac{T_a}{2} . \end{gathered} $ | (3) |
其中:σ是动目标的散射系数,τ是距离向时间,t是方位向时间,λ是发射信号的载波的波长,Ta是合成孔径时间。
1.2 基于二维搜索的动目标参数估计方法(传统方法)将式(3)中动目标的方位向线性调频信号简化表示为
| $ s(t)=\sigma \cdot \exp \left(\mathrm{j} 2 {\rm{ \mathit{π} }} f t+\mathrm{j} {\rm{ \mathit{π} }} k_a t^2+\varphi_0\right) . $ | (4) |
其中:f是多普勒中心频率,ka是多普勒调频率,φ0是常数相位。
单个角度下的FrFT处理,可以得到
| $ \begin{gathered} X_p(u)=\int_{-\infty}^{+\infty} K_p(t, u) s(t) \mathrm{d} t= \\ \sigma \cdot \int_{-\infty}^{+\infty} K_p(t, u) \exp \left(\mathrm{j} 2 {\rm{ \mathit{π} }} f t+\mathrm{j} {\rm{ \mathit{π} }} k_a t^2+\varphi_0\right) \mathrm{d} t . \end{gathered} $ | (5) |
其中: Kp(t, u)是FrFT的核函数。
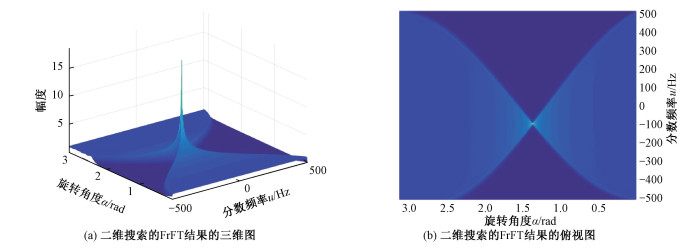
如图 2所示,传统的二维搜索方法是以固定的搜索间隔,遍历0~π内的所有角度进行FrFT处理。所有的FrFT计算结果构成二维平面,通过峰值搜索获得最优旋转角
|
Download:
|
| 图 2 基于二维搜索的FrFT处理方法 Fig. 2 FrFT method based on 2D searching | |
利用
| $ \begin{aligned} & \hat{f}=\frac{\operatorname{PRF}}{N} \hat{u} \cdot \csc \hat{\alpha}, \\ & \hat{k}_a=-\frac{\text { PRF }^2}{N} \cot \hat{\alpha} . \end{aligned} $ | (6) |
其中:PRF是脉冲重复频率,即方位向采样率;N是采样点数,即信号时域的长度。
动目标的多普勒参数和距离向速度vy、方位向速度vx、方位向真实位置Xt之间的关系:
| $ \begin{gathered} v_y=\frac{2 v_a X-f \lambda R_0}{2 Y}, \\ v_x=v_a-\sqrt{-\frac{k_a \lambda R_0}{2}}, \\ X_t=X-\frac{v_y Y}{v_a}. \end{gathered} $ | (7) |
其中:动目标的初始位置为(X, Y, 0),动目标和雷达平台之间的最短斜距为R0。
综上,根据估计的最优旋转角度
| $ \begin{gathered} \hat{v}_y=\frac{2 v_a N X-\lambda R_0 \cdot \mathrm{PRF} \cdot \hat{u} \cdot \csc \hat{\alpha}}{2 N Y}, \\ \hat{v}_x=v_a-\sqrt{-\frac{\hat{k}_a \lambda R_0}{2}}=v_a-\sqrt{\frac{\operatorname{PRF}^2 \lambda R_0 \cot \hat{\alpha}}{2 N}}, \\ X_t=\frac{\lambda R_0 \cdot \mathrm{PRF} \cdot \hat{u} \cdot \csc \hat{\alpha}}{2 N v_a} . \end{gathered} $ | (8) |
随着角度搜索间隔的减小,二维搜索的精度提高,动目标参数估计的精度也随着提高,但是运算量也随着增加,不利于实时动目标测速。
第2节中提出的方法将利用几何信息估计最优旋转角
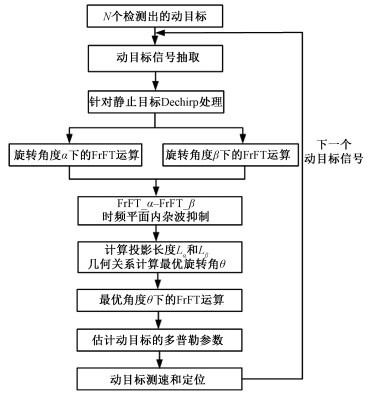
通过分析信号的时频长度和FrFT投影之间的关系,可以从几何角度计算FrFT最优旋转角。整个算法的步骤如图 3所示。
|
Download:
|
| 图 3 基于几何信息的FrFT动目标参数估计算法 Fig. 3 Parameter estimation method of moving target using FrFT based on Geometric information | |
1、dechirp处理
对动目标所在的距离门进行抽取,并针对距离门内的剩余杂波信号进行dechirp处理,将杂波信号转换为单频信号。
2、杂波抑制
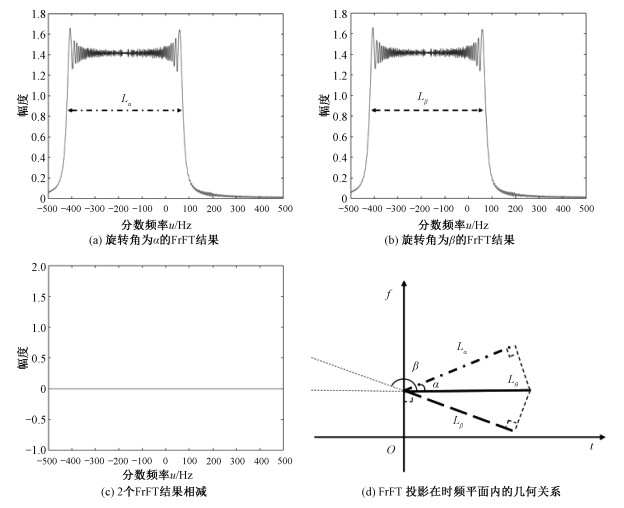
1) 如图 4所示,选择关于π对称的2个旋转角度α和β,分别对抽取的动目标信号做FrFT运算,得到结果FrFT_α和FrFT_β;
|
Download:
|
| 图 4 时频平面内静止目标杂波抑制 Fig. 4 Clutter suppression for stationary targets in time-frequency plane | |
2) FrFT_α和FrFT_β相减,在时频平面内杂波抑制,并从相减的结果中计算投影长度Lα和Lβ。
3、动目标测速和定位
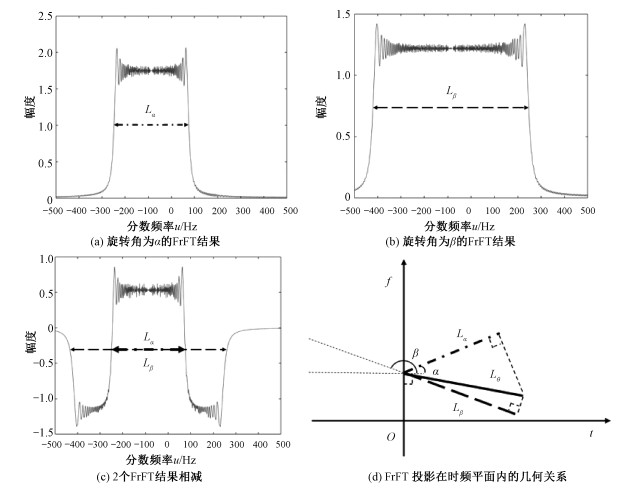
1) 如图 5所示,利用Lα、Lβ和信号时频长度之间的几何关系,计算动目标信号的最优旋转角θ;
|
Download:
|
| 图 5 时频平面内运动目标的几何关系 Fig. 5 Geometric relations of moving targets in time-frequency plane | |
2) 做角度θ下的FrFT运算,得到动目标的多普勒中心频率和调频率的估计值;
3) 根据估计的多普勒参数计算动目标的方位向速度、距离向速度和方位向位置。
2.1 dechirp处理首先,针对剩余杂波信号进行去调频校正,使之变为单频信号。根据单频信号在时频平面的几何特点(时频角是固定的90°),当选择的2个旋转角度关于π对称(α+β=π),单频信号在这2个角度α和β下的投影长度相等。通过2个投影的相减,在时频平面内对剩余杂波信号进一步抑制。
由于动目标信号没有得到匹配校正,动目标信号仍然是线性调频信号。2个角度α和β下的投影相减后,动目标信号没有被完全抑制。利用几何信息,仍然可以对动目标信号进行多普勒参数估计和速度测量。
假设动目标信号所在的距离门内还有剩余杂波信号和噪声,对动目标信号重新建模如下。
| $ \begin{aligned} s(t)= & \sigma_s \cdot \exp \left(-\mathrm{j} \frac{4 {\rm{ \mathit{π} }}}{\lambda}\left(R_0+\frac{\left(v_x-v_a\right) X+v_y Y}{R_0}\left(t-t_0\right)+\frac{\left(v_a-v_x\right)^2+v_y^2}{2 R_0}\left(t-t_0\right)^2\right)\right)+ \\ & \sum\limits_{n=1}^N \sigma_{c n} \cdot \exp \left(-\mathrm{j} \frac{4 {\rm{ \mathit{π} }}}{\lambda}\left(R_0-\frac{v_a X}{R_0}\left(t-t_n\right)+\frac{v_a^2}{2 R_0}\left(t-t_n\right)^2\right)\right),\left|t-t_n\right| \leqslant \frac{T_a}{2}. \end{aligned} $ | (9) |
其中:σs是动目标散射系数。假设一共有N个剩余杂波,σcn表示第n个杂波的散射系数,tn是第n个杂波的雷达波束穿越时刻。
针对剩余杂波进行去调频校正,使得校正后的剩余杂波信号为单频信号,补偿信号如下
| $ s_a(t)=\exp \left(\mathrm{j} \frac{2 {\rm{ \mathit{π} }} v_a^2 t^2}{\lambda R_0}\right),|t| \leqslant \frac{T_a}{2}. $ | (10) |
校正后的信号为
| $ \begin{gathered} s(t)=\sigma_s \cdot \exp \left(-\mathrm{j} \frac{4 {\rm{ \mathit{π} }}}{\lambda}\left(R_0+\frac{\left(v_x-v_a\right) X+v_y Y}{R_0}\left(t-t_0\right)+\frac{\left(v_a-v_x\right)^2+v_y^2}{2 R_0}\left(t-t_0\right)^2-\frac{v_a^2}{2 R_0} t^2\right)\right)+ \\ \sum\limits_{n=1}^N \sigma_{c n} \cdot \exp \left(-\mathrm{j} \frac{4 {\rm{ \mathit{π} }}}{\lambda}\left(R_0-\frac{v_a X}{R_0}\left(t-t_n\right)+\frac{v_a{ }^2}{R_0} t_n t+\frac{v_a{ }^2}{2 R_0} t_n^2\right)\right),\left|t-t_n\right| \leqslant \frac{T_a}{2}. \end{gathered} $ | (11) |
此时,动目标信号的多普勒中心频率不变,多普勒调频率变为
| $ k^{\prime}=\frac{-2\left(v_a-v_x\right)^2+2 v_a^2}{\lambda R_0}. $ | (12) |
对校正后的信号进行FrFT处理
| $ X_p(u)=\int_{+\infty}^{-\infty} K_p(t, u) s(t) \mathrm{d} t . $ | (13) |
从图 4可以看出,校正后的静止目标为单频信号,在2个对称角度下的FrFT结果相减,可以把静止目标抑制掉。取FrFT幅度的一半为阈值,计算FrFT投影长度,从图 4(d)中可以看出2个投影长度相等,相减的值为0。Lθ为信号在时频平面的长度。
2.3 动目标测速和定位从图 5可以看出,由于动目标信号的调频率和静止杂波的调频率不同,且校正信号是针对剩余杂波进行去调频,所以动目标信号没有得到匹配校正,仍为线性调频信号。此时,2个对称角度下(α+β=π)的FrFT结果相减,不会把动目标信号抑制掉。相减后的结果中,仍然可以测量出2个角度下的FrFT投影长度Lα和Lβ。Lθ为信号在时频平面的长度。
根据图 5(d)中的几何关系,可以得到
| $ \begin{gathered} \cos (\theta-\alpha)=-\frac{L_\alpha}{L_\theta}, \\ \cos (\beta-\theta)=\frac{L_\beta}{L_\theta}. \end{gathered} $ | (14) |
2个式子相除,可以消除未知量Lθ。三角公式展开,通过整理可以得到
| $ \tan (\theta)=-\frac{L_\beta \cos \alpha+L_\alpha \cos \beta}{L_\alpha \sin \beta+L_\beta \sin \alpha}. $ | (15) |
通过反三角函数,可以得到时频角的估计值
| $ \hat{\theta}=\arctan \left(-\frac{L_\beta \cos \alpha+L_\alpha \cos \beta}{L_\alpha \sin \beta+L_\beta \sin \alpha}\right) . $ | (16) |
时频角和FrFT的最优旋转角之间相差90°,因此可以得到
| $ \begin{aligned} & \hat{v}_y=\frac{v_a X}{Y}-\frac{\lambda R_0 \cdot \mathrm{PRF} \cdot \hat{u}}{2 N Y} . \\ & \frac{\sqrt{L_\alpha^2+L_\beta^2+2 L_\alpha L_\beta \cos (\alpha-\beta)}}{L_\alpha \sin \beta+L_\beta \sin \alpha}, \\ & \hat{v}_x=v_a-\sqrt{-\frac{\hat{h}_a \lambda R_0}{2}}=v_a- \\ & \sqrt{\frac{L_\alpha \sin \beta+L_\beta \sin \alpha}{L_\beta \cos \alpha+L_\alpha \cos \beta} \cdot \frac{\mathrm{PRF}^2 \lambda R_0}{2 N}}, \\ & \;\;\;\;\;\;\;X_t=\frac{\lambda R_0 \cdot \mathrm{PRF} \cdot \hat{u}}{2 N v_a}. \\ & \frac{\sqrt{L_\alpha^2+L_\beta^2+2 L_\alpha L_\beta \cos (\alpha-\beta)}}{L_\alpha \sin \beta+L_\beta \sin \alpha} . \end{aligned} $ | (17) |
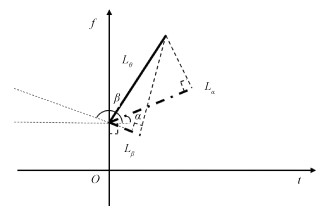
需要注意的是,上面的情况,Lα和Lβ是Lθ的异侧投影。而图 6中所示,Lα和Lβ是Lθ的同侧投影。
|
Download:
|
| 图 6 同侧投影时动目标信号的几何关系 Fig. 6 Geometric relations of moving targets in ipsilateral projection | |
同侧投影得到的结果如下
| $ \tan (\theta)=\frac{L_\beta \cos \alpha-L_\alpha \cos \beta}{L_\alpha \sin \beta-L_\beta \sin \alpha}. $ | (18) |
在得到时频角的估计值
此时,利用3次FrFT求得最优旋转角和目标的运动参数,大大缩减了目标参数估计的时间。并且通过在时频平面内进行杂波抑制,进一步提高动目标参数估计的精度。
理论上,角度α和β可取的值很多。实际中,不同的旋转角对应不同的FrFT结果及其投影长度。从式(16)可以看出最优旋转角的反演和投影长度的测量有关。假设长度的测量误差是一定的,则投影长度越长,误差比例越小。实际中由于不知道最优旋转角的真值,所以不知道最合适的角度α和β。因此为了提高精度,可以多尝试几组不同的旋转角度,然后选择投影长度较长的结果进行平均。
3 实验与分析 3.1 仿真数据验证与分析根据式(4)仿真8个动目标的线性调频信号。动目标的方位向速度在-20~20 m/s,距离向速度在-30~30 m/s。仿真实验的SAR系统参数如表 1所示。
|
|
表 1 仿真实验SAR系统参数 Table 1 SAR system parameters for the simulation experiment |
设置3组对比实验。第1组实验记作FrFT-1,使用传统的二维搜索FrFT处理方法,搜索角度范围是[0, π],搜索间隔是0.01 rad。第2组实验记作FrFT-2,使用传统的二维搜索FrFT处理方法,搜索角度范围是[0, π],搜索间隔是0.001 rad。第3组实验记作WS-FrFT,使用本文提出的基于几何信息的FrFT方法。
3组实验对仿真的8个动目标信号的测速结果和运行时间,如表 2所示。
|
|
表 2 动目标参数估计和运行时间 Table 2 Parameters estimation and running time of the moving targets |
算法比较使用的评测指标是平均绝对误差MAE
| $ \operatorname{MAE}(\hat{X}, X)=\frac{1}{n} \sum\limits_i\left|\hat{x}_i-x_i\right|. $ | (19) |
其中:
|
|
表 3 方法性能指标对比 Table 3 Performance comparison of the algorithms |
从结果可以看出,随着二维搜索间隔的减小,搜索精度提高,估计的速度越接近真实值。本文所提方法的估计误差介于FrFT-1和FrFT-2之间,且接近于FrFT-2,误差水平在可以接受的范围内。运行时间却大大减小,在0.01 s的级别。
3.2 实测数据验证与分析本实验使用的是真实SAR数据。如图 7(a)所示,截取的SAR场景中方位向2 501个像素点,距离向1 101个像素点。

|
Download:
|
| 图 7 SAR图像杂波抑制和chirp信号提取的结果 Fig. 7 The results of clutter suppression and extracted chirp signals in SAR image | |
对双通道的SAR复图像数据,用二维自适应方法[13-14]进行通道均衡和误差校正。对校正后的两幅图像,进行杂波抑制和动目标检测[15-17],结果如图 7(b)所示,得到8个可疑的动目标。
对动目标检测的结果,进行方位向解压缩,即方位向匹配滤波器的逆处理,结果如图 7(c)所示。对8个可疑动目标所在的距离门进行提取,得到8个动目标信号的方位向chirp信号。
如图 7(b)所示,杂波抑制后,整个平原的杂波背景被抑制掉,左侧的铁路和右侧的两条公路被抑制掉。但是右侧的铁路由于杂波较强,没有完全抑制掉,还有剩余杂波存在。
因此,图 7(c)中每个动目标信号所在的距离单元可能有右侧铁路的剩余杂波。用FrFT对动目标的线性调频信号进行处理时,多普勒参数的估计和速度的测量可能受到剩余杂波的影响。
利用本文提出的动目标参数估计方法,在时频平面内对剩余杂波信号进一步抑制,有利于提高动目标信号参数估计和速度测量的精度。
3组对比实验的设置和仿真实验相同,实验结果如表 4所示。
|
|
表 4 动目标参数估计和运行时间 Table 4 Parameters estimation and running time of the moving targets |
从实验结果可以看出,目标2的最优旋转角度的估计值是90°,符合单频信号的特征。距离向速度的估计值接近0,判断这个目标为静止目标(虚警)。剩余7个目标的距离向速度是正值,说明汽车的行驶方向是从下到上。
实际数据处理中,动目标运动参数没有真实值作为参考。基于仿真实验和二维FrFT精细搜索(0.001 rad搜索间隔),我们相信FrFT精细搜索得到的结果是接近真实值的。
从实结果可以看出,本文提出的方法的测速和定位精度可以达到精细搜索的FrFT方法的估计精度。而且计算量大大减小,运行时间缩短到0.01 s级别。
4 结论本文通过分析FrFT投影在时频平面的几何特点,提出了基于时频平面几何信息的快速动目标测速和定位方法。首先将检测出的动目标信号进行抽取,并针对静止目标进行去调频处理。然后选择对称角度α和β(α+β=π)分别进行FrFT运算,将2个投影长度相减进行杂波抑制,根据时频平面内的几何特点求解动目标的最优旋转角。利用估计的最优旋转角再次进行FrFT运算,进而对动目标信号进行速度估计和位置估计。
本文方法大大降低了动目标的参数估计时间,单个目标的参数估计耗时是0.01 s级别。本文方法的测速和定位精度可以达到精细搜索方法的估计精度,为实时动目标检测和参数估计提供了一定的基础。
| [1] |
Zheng M J, Yan H, Zhang L, et al. Research on strong clutter suppression for Gaofen-3 dual-channel SAR/GMTI[J]. Sensors (Basel, Switzerland), 2018, 18(4): 978. Doi:10.3390/S18040978 |
| [2] |
He X P, Liao G S, Zhu S Q, et al. Range-ambiguous clutter suppression for the SAR-GMTI system based on extended azimuth phase coding[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(11): 8147-8162. Doi:10.1109/TGRS.2020.2987630 |
| [3] |
Sun Q Y, Shu T, Tang M, et al. Effective moving target deception jamming against multichannel SAR-GMTI based on multiple jammers[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(3): 441-445. Doi:10.1109/LGRS.2019.2921678 |
| [4] |
Guo Y F, Liao G S, Li J, et al. A clutter suppression method based on NSS-RPCA in heterogeneous environments for SAR-GMTI[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(8): 5880-5891. Doi:10.1109/TGRS.2020.2972.060 |
| [5] |
Yang Z W, Xu H J, Huang P H, et al. Preliminary results of multichannel SAR-GMTI experiments for airborne quad-pol radar system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(6): 3822-3840. Doi:10.1109/TGRS.2019.2958488 |
| [6] |
Tian M, Yang Z W, Duan C D, et al. A method for active marine target detection based on complex interferometric dissimilarity in dual-channel ATI-SAR systems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(1): 251-267. Doi:10.1109/TGRS.2019.2936150 |
| [7] |
Wacks S, Yazıcı B. Doppler-DPCA and Doppler-ATI: novel SAR modalities for imaging of moving targets using ultra-narrowband waveforms[J]. IEEE Transactions on Computational Imaging, 2018, 4(1): 125-136. Doi:10.1109/TCI.2017.2782639 |
| [8] |
Yu L J, Zhang Y H. Application of the fractional Fourier transform to moving train imaging[J]. Progress in Electromagnetics Research M, 2011, 19: 13-23. Doi:10.2528/pierm1151401 |
| [9] |
Li Q N, He L, Qi L J, et al. Unique decomposition and a new model for the ground moving target indication problem[J]. Journal of Optimization Theory and Applications, 2017, 173(1): 297-312. Doi:10.1007/S10957-016-1052-5 |
| [10] |
Chiu S. Moving target parameter estimation for RADARSAT-2 moving object detection experiment (MODEX)[J]. International Journal of Remote Sensing, 2010, 31(15): 4007-4032. Doi:10.1080/01431160903032901 |
| [11] |
Chiu S. Application of fractional Fourier transform to moving target indication via along-track interferometry[J]. EURASIP Journal on Advances in Signal Processing, 2005, 2005(20): 3293-3303. Doi:10.1155/ASP.2005.3293 |
| [12] |
Zhang X P, Yang C, Lin Q Q, et al. Efficient parameters estimation methods for radar moving targets without searching[J]. IEEE Access, 2020, 8: 41351-41361. Doi:10.1109/ACCESS.2019.2957383 |
| [13] |
Cerutti-Maori D, Klare J, Brenner A R, et al. Wide-area traffic monitoring with the SAR/GMTI system PAMIR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 3019-3030. Doi:10.1109/TGRS.2008.923026 |
| [14] |
Wang C H, Liao G S, Zhang Q J. First spaceborne SAR-GMTI experimental results for the Chinese Gaofen-3 dual-channel SAR sensor[J]. Sensors (Basel, Switzerland), 2017, 17(11): 2683. Doi:10.3390/S17112683 |
| [15] |
郑明洁, 杨汝良. 基于DPCA和干涉技术的SAR动目标检测[J]. 电子与信息学报, 2003, 25(11): 1525-1530. |
| [16] |
孙娜, 周荫清, 李景文. 基于DPCA技术的星载SAR/GMTI处理方法[J]. 电子与信息学报, 2005, 27(10): 1564-1568. |
| [17] |
王艳霞, 张毅. 机载单天线SAR动目标检测与参数估计[J]. 中国科学院研究生院学报, 2012, 29(2): 227-233. Doi:10.7523/j.issn.2095-6134.2012.2.012 |
 2023, Vol. 40
2023, Vol. 40 


