2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
成像卫星是遥感系统实现对地观测的重要手段之一,主要采用星载遥感器从太空对地球、月球等天体实现成像,目前已经广泛应用于气象预报、环境监测、军事侦察等不同领域。近年来,用户对成像卫星数据的需求量越来越大,所要求的数据质量也越来越高。考虑到卫星的发射成本和指数级增长的用户需求,合理利用卫星资源显得尤为重要。这就要求合理分配卫星资源,解决成像卫星任务规划问题,以在有限的卫星资源下最大限度地满足用户对卫星数据的需求。
国内外学者对卫星成像规划问题已有大量的研究,在模型建立和算法求解两方面有很多成果。Bensana等[1]研究SPOT5卫星常规任务的任务规划,认为该问题可以表述为非线性规划问题,建立了整数规划模型,但在模型中考虑到的约束条件较少。贺仁杰[2]认为多星联合任务规划是一个具有时间窗口约束的并行机器调度问题,建立了多星任务规划问题的约束满足模型,但未考虑卫星存储和数据下传及成像时云量大小等约束。学者Vasquez和Hao[3]把侦察卫星的任务方案规划和执行问题转化为背包问题模型,但主要讨论卫星任务规划问题和背包问题模型的转化,涉及卫星的约束较少。在算法方面,Wolfe和Soersnen[4]通过实验证明相比于贪婪算法,遗传算法可以较大幅度地改进调度结果,但后续的研究表明当问题达到一定规模时,遗传算法的寻优效果降低。白保存[5]针对成像卫星的任务规划问题中点目标与区域目标同时存在的情况,提出动态合成启发式算法与快速模拟退火算法对问题进行整体优化求解,但是动态合成启发式算法调度结果不理想,快速模拟退火算法对大规模求解问题存在不足。李志亮等[6]考虑观测时间因素,将离散差分进化与变邻域搜索相结合,使用混合算法求解构建的约束满足模型,但在实验模型中未考虑云量约束。李海玲和党琦[7]通过分解和分析成像任务规划过程和目标的重要程度和紧急程度,设计了一种基于目标优先级的快速成像任务规划流程,但文中并未涉及实际的应用案例。明卫鹏等[8]分析卫星成像规划的约束条件,建立了相应的约束满足模型,使用基因表达式编程求解该问题,但其模型考虑的约束较少,模型的应用价值有待提高。申经伟[9]改进了布谷鸟搜索算法,利用经典函数对比检验,表明改进的布谷鸟搜索算法可以在较少的迭代次数中搜索到精确度较高的全局最优值,最后将其应用于集装箱港口群铁路班列网络运输模型的求解中,验证了算法的有效性。徐杨丽和叶春明[10]使用布谷鸟搜索算法解决置换流水车间调度问题,验证了在不同参数的支配下,布谷鸟搜索算法寻优效果均强于猫群算法。明波等[11]使用改进的布谷鸟搜索算法求解梯级水库调度模型,在实验中验证了布谷鸟搜索算法的可行性和有效性。邵萌等[12]将布谷鸟搜索算法引入包含地理信息惩罚因子的变电站选址模型,实验表明布谷鸟搜索算法可有效克服传统算法中的“早熟”现象,全局寻优能力和搜索率更高。为增强算法的全局搜索能力,改善求解结果,本文首次提出使用布谷鸟搜索算法解决卫星成像规划问题。
本文介绍布谷鸟搜索算法的基本原理,构建卫星成像规划模型,设计改进布谷鸟搜索算法求解该问题的具体步骤,最后在实验中将之与布谷鸟搜索算法和遗传算法对比,并对实验结果进行分析,证明了本文方法的可行性和优越性。
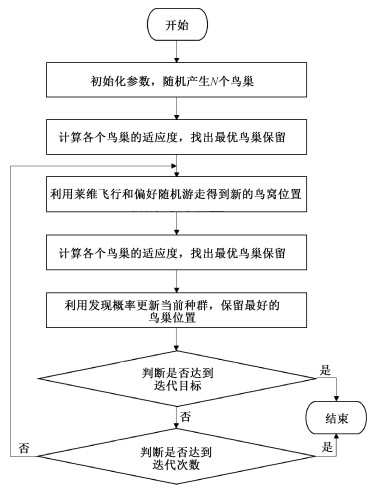
1 布谷鸟搜索算法简介布谷鸟搜索算法(cuckoo search, CS)是2009年英国学者Yang和Deb在群体智能技术的基础上提出的一种新型群智能优化算法[13]。该算法模拟某些布谷鸟寄生育雏(brood parasitism) 时巢寄生的繁殖习性,利用莱维飞行(Levy fights)和偏好随机游走进行种群更新,有效求解最优化问题,具有全局搜索能力强、所需参数较少易于进行调节等特点。算法的流程图如图 1所示。
|
Download:
|
| 图 1 布谷鸟搜索算法流程图 Fig. 1 Flow chart of cuckoo search algorithm | |
在CS算法模型中,一个宿主巢的原有蛋表示一个候选解,一个布谷鸟新产的蛋表示一个新解,该算法的目标是利用新解或者可能产生的优解替代巢中原有的劣解。为了简单描述布谷鸟搜索算法并将其应用到实际的优化问题中,Yang和Deb在提出布谷鸟搜索算法时引入了以下3条理想化规则:1)布谷鸟一次只产一个蛋,并随机选择宿主鸟巢存放;2)目前具有优质蛋的巢穴会被保留到下一代;3)布谷鸟可以选择的巢穴数量是固定的,且宿主鸟发现外来蛋的概率也是固定的[13]。一旦布谷鸟蛋被发现,宿主鸟将抛弃布谷鸟蛋或旧巢。
另外,在自然界中,许多动物的飞行都具有幂律规律,这是莱维飞行的典型特征。莱维分布是由数学家Levy提出的一种概率分布,莱维飞行是一种服从莱维分布的随机搜索方法,主要靠短间距的搜索与偶尔较长间距的行走相间的方式,在搜索过程中产生较大的跃动和较剧烈的运动方向的变化,使得算法跳出局部最优。Yang将其应用在鸟窝位置的更新上,从而布谷鸟搜索算法也具有良好的全局搜索能力。
在以上3条理想化规则下,布谷鸟寻窝的路径和位置更新公式[14]如下
| $ x_i^{t+1}=x_i^t+\alpha \oplus L(u, v), i=1, 2, \cdots, N. $ | (1) |
其中:xit表示第i个鸟窝在第t代的位置;α表示步长因子,用来控制步长;L(u, v)为随机步长路径,采用Mantegna算法执行莱维飞行,步长计算公式[15]如下
| $ L(u, v)=\frac{u}{|v|^{\frac{1}{\beta}}}. $ | (2) |
| $ u \sim N\left(0, \sigma_u^2\right), v \sim N\left(\sigma_v^2\right) . $ | (3) |
其中
| $ \sigma_u=\left\{\frac{\varGamma(1+\beta) \sin (\pi \beta / 2)}{\varGamma \beta[(1+\beta) / 2] 2^{(\beta-1) / 2}}\right\}^{1 / \beta}, \sigma_v=1 . $ | (4) |
布谷鸟进行莱维飞行完成位置更新后,为抛弃被发现鸟窝,在[0, 1]区间产生随机数R并与宿主鸟发现外来蛋的概率Pa进行对比,若R > Pa,则改变xit位置,否则不变。
2 成像规划模型建立卫星成像规划模型,就是将实际的成像规划问题简化为数学模型,把问题的需求、条件、结果转化为模型输入输出、约束条件等,主要包含预处理、约束条件的分析、约束满足模型的建立3个步骤[16]。
在建立约束满足模型前,用户首先提出包含目标区域、图像类型、图像约束、观测有效时间等内容的观测需求集合。通常来说,相对于用户需求,卫星资源是非常稀缺的。卫星成像规划的目标就是生成一个满意的调度方案,以合理分配卫星资源。
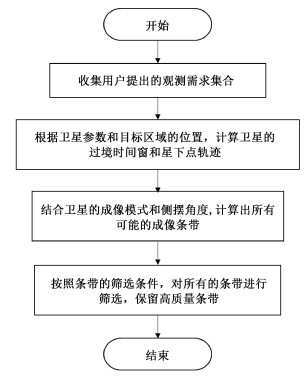
2.1 预处理预处理根据观测需求集合,分析用户需求及所能够调度的卫星资源的属性,获取目标区域的地理位置和卫星的轨道信息,对任务进行分解及规范化处理,为后期问题建模提供数据基础。成像规划问题的预处理过程主要包括以下几个方面:轨道计算、对目标区域的访问时间计算、基于条带的区域分解计算和成像条带的筛选。按照侧摆角大小、图像分辨率高低等条件对计算出的条带进行筛选。
成像卫星在单次过境时,根据侧摆角的不同,能够产生多个可选的观测活动,即产生多个条带,但每次过境只能选择其中的一个条带或不选择条带参与最终的成像。此时,卫星成像规划的调度方案便转化为条带的组合方案。
根据以上所述,预处理的流程图如图 2所示。
|
Download:
|
| 图 2 预处理基本步骤 Fig. 2 Basic steps of preprocessing | |
预处理时已根据一些条件筛选出较高质量的成像条带,但成像方案是不同的条带组合,组合过程中也需要根据实际情况考虑多方面约束条件,现将考虑的约束整理在表 1中[8, 17-18]。
|
|
表 1 约束规则 Table 1 Constraint rules |
在分析了卫星成像时需要考虑的主要约束后,便可建立约束满足模型,将问题中涉及到的模型输入、模型输出、约束条件、目标函数等用数学符号表示出来。
1) 模型输入:所有可能的成像条带集。包含卫星标识、传感器型号、传感器成像模式、侧摆角、成像开始与结束时间、成像区域范围等重要信息。
2) 模型输出:需安排的条带集合。该集合包含卫星在每个轨道圈次是否成像,成像时选择的传感器、传感器模式、传感器侧摆角、成像开始时间、成像结束时间等信息。
3) 约束条件:首先对约束满足模型中用到的符号进行定义。设两个成像条带sidi、sidj相对应的卫星标识分别为satNamei、satNamej,对应的传感器型号分别为senNamei、senNamej,传感器成像模式分别为modei、modej,成像开始与结束时间分别为startTimei、startTimej、endTimei、endTimej,侧摆角sideRighti、sideRightj。
① 成像条带总和小于等于可成像条带总数。
| $ \text { stripNumber } \leqslant k \text {. } $ | (5) |
其中:stripNumber为每次参与成像条带总数,k为可成像条带总数。
② 任意卫星的成像条带时间长度大于该卫星要求的最小拍摄时间。
| $ \text { endTime }_i-\text { startTime }_i \geqslant \text { minSatpictime. } $ | (6) |
其中:minSatpictime为卫星的单次最小拍摄时间。
③ 成像条带的最早开始时间晚于指定开始时间,最晚结束时间早于指定的结束时间。
| $ \text { startTime }_i \geqslant \text { startTime, endTime }_i \leqslant \text { endTime. } $ | (7) |
其中:startTime、endTime为成像规划的指定开始、结束时间。
④ 单次最长开机时间约束。卫星对区域目标进行观测时,时间窗应在单次最长开机时间范围内。
| $ \begin{gathered} \max \left\{\begin{array}{c} \text { endTime }_i, \\ \text { endTime }_j \end{array}\right\}-\min \left\{\begin{array}{c} \text { startTime }_i, \\ \text { startTime }_j \end{array}\right\} \leqslant \\ \text { maxSatontime. } \end{gathered} $ | (8) |
其中:maxSatontime为卫星单次最长开机时间。
⑤ 载荷每轨、每天工作合计时长约束。
当satNamei=satNamej,senNamei=senNamej时,
| $ \text { endTime }_i \text { - } \text { startTime }_i \leqslant \text { maxSenontperpas. } $ | (9.a) |
| $ \begin{gathered} \left(\text { endTime }_i-\text { startTime }_i\right)+\cdots+ \\ \left(\text { endTime }_j-\text { startTime }_j\right) \leqslant \text { maxSenontperday. } \end{gathered} $ | (9.b) |
其中:maxSenontperpas、maxSenontperday为载荷每轨、每天工作最长时间。
关于成像时卫星的传感器和传感器模式、光照条件、云量等其他约束,可以设计将其融入到解的编码方式和目标函数中,这样不仅可以降低模型的复杂度,也可以提高模型的可移植性,利于后期使用不同算法解决此模型并进行比较。
上述约束条件都是建立在成像条带基础上的。计算过程中所需要的信息都已包含在成像条带中,这也是以成像条带为基础建立约束条件的前提。
4) 目标函数:通常情况下,根据用户的不同需求,评价一个成像方案优劣的指标有很多,但最基础的是成像方案对目标区域的覆盖率,本文的侧重点在于验证本文方法对于成像规划问题的适用性和优越性,因此设置基础的目标函数,把成像方案对区域目标的覆盖率作为评价其优劣的指标,同时,考虑云量因素和光照因素,以惩罚因子的形式加入到目标函数中,即
| $ P=\frac{\bigcup\limits_{i=1}^n s_i}{s}-\omega_c \times \sum\nolimits_{i=1}^n c_i-\omega_t \times \sum\nolimits_{i=1}^n t_i . $ | (10) |
其中:
所建的约束满足模型为maxP,s.t.(5)、(6)、(7)、(8)、(9)。
3 改进算法求解 3.1 算法的编码设计求解所建模型时,编码方式对算法的寻优性能具有一定的影响。卫星成像规划的结果是一组条带的组合,解的编码应根据条带信息所包含的内容进行设计。成像方案的所有信息都由最终组成解的成像条带确定,本文以卫星的过境次数作为编码的基础,以该轨道下可以产生的成像条带个数为编码内容设计解的基本编码[16]。
按照卫星的轨道,将所有条带进行分组,卫星每次过境都可以产生若干个可用的成像条带,从其中选择出1个或0个条带作为解编码中的一个码,选择0个则相应的编码为-1,表示该次过境轨道不成像。这样所有的过境轨道选择完毕后,就形成了一个码序列。这样的一个码序列是解的基本编码序列,也代表针对目标区域的一个可行的成像方案。
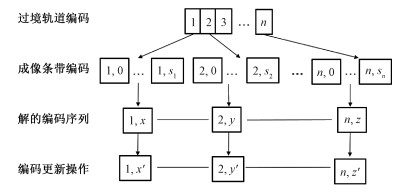
3.2 更新操作的设计在以上编码方式中,解的编码序列由一组整数对组合而成,每个整数对代表一个条带,其中第1个整数代表该条带所属的卫星轨道序号,第2个整数代表该轨道产生的若干条带中参与规划的特定条带序号。对所有整数对的第2个整数进行莱维飞行操作,其邻域范围为该整数对第1个整数对应的轨道圈次可以产生的条带个数总数加1,这样就保证经过莱维飞行更新,产生的新条带仍然在约束范围内。为保证经过莱维飞行后的数值仍为整数,对更新后的数值进行取整操作,通过这样的改变,莱维飞行的邻域转化为离散空间,且可以直接通过布谷鸟搜索算法的位置更新公式获得新解。假设某一条带的编码为(3, p),更新后的编码为(3, q),p、q均属于该轨道圈次可产生的条带个数,若q=-1,则表示更新后该轨道圈次不参与成像,若q=p,则表示经过该次更新,所选条带不变。若q≠-1且q≠p,则表示选择新的条带参与成像。对解的编码序列中每一个整数对都进行莱维飞行更新,可产生一个新的编码序列,即产生一个新的解。具体的编码和更新方式如图 3所示。
|
Download:
|
| 图 3 解的基本编码及更新图 Fig. 3 Schematic diagram of the basic coding and updating strategies | |
在标准布谷鸟搜索算法中,莱维飞行的方向和步长是随机的,这可能导致算法后期收敛速度较慢,影响其寻优效果。据此,考虑在算法迭代的不同阶段,引入非线性惯性权重,采用非线性的步长更新方法,使得算法在前期能够快速寻优,而后期可以跳出局部最优[19]。具体的步长更新公式如下
| $ \begin{gathered} x_i^{h+1}=\varphi \times\left(x_i^h-x_{\text {best }}^h\right)+\alpha \oplus L(u, v), \\ i=1, 2, \cdots, N . \end{gathered} $ | (11) |
其中: φ为非线性权重系数,取值如下
| $ \varphi=\left\{\begin{array}{c} \varphi_0, h<h_0 \\ \left(\frac{2}{h}\right)^{0.4}, h \geqslant h_0 \end{array} .\right. $ | (12) |
其中: φ0为充分大的正实数,h为当前迭代次数,h0为指定迭代次数。
通过引入非线性惯性权重,对标准的布谷鸟搜索算法进行改进,从而建立改进的布谷鸟搜索算法(improved cuckoo search,ICS)。
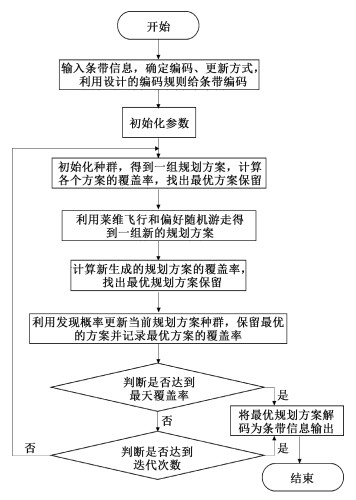
3.4 求解过程卫星成像规划问题模型的求解步骤如下:
1) 读取条带信息,确定解的基本编码和更新方式。通过编码将实际问题转换为可使用改进布谷鸟搜索算法求解的数学问题,并根据布谷鸟搜索的特点,确定解的更新方式。
2) 初始化各参数,设定初始种群规模N,循环次数T,发现概率Pa。
3) 初始化种群,随机生成N个初始解,得到一组规划方案,并计算这N个解的适应度。这里的适应度取规划方案对目标区域的覆盖率。
4) 第一次迭代开始,设h=0,当h < times时。
5) 找出该组规划方案中覆盖率最高的方案x,对该方案中每个条带的编码进行更新,根据莱维飞行获得下一个方案y,莱维飞行公式中的步长β取1.5。在进行莱维飞行更新时为了在下一轮中保留上一轮最好的方案,因此在步长前乘以系数xih-1-xbesth-1,i为对应的点坐标,h为当前迭代次数,使用的步长方向用0~1均匀概率分布产生,步长方向点乘步长再乘以系数就是步长增量。
6) 比较x和y的覆盖率,保留两个方案中覆盖率较大的一个,以此更新目前最优方案x。
7) 产生一个服从均匀分布的随机数R作为宿主鸟发现外来鸟蛋的可能性,也即新解保留下来的可能性,将其与抛弃概率pa进行比较。若R < pa,则使用随机游走方法改变鸟窝位置产生新规划方案z,反之不变。最后保留最好的规划方案,即再次更新最优解x。h=h+1。
8) 判断算法是否满足设置的最大迭代次数:若不满足,重复进行迭代寻优; 若满足,结束搜索过程,输出最优解,得到最优成像方案。
基于改进布谷鸟搜索算法的卫星成像规划流程如图 4所示。
|
Download:
|
| 图 4 基于改进布谷鸟搜索算法的卫星成像规划流程图 Fig. 4 Flow chart of satellite imaging planning based on improved cuckoo search algorithm | |
本文仿真实验在Windows10操作系统下完成,设备处理器为Inter(R)Core(TM)i5,设备内存为8 G,运行环境为PyCharm Community Edition 2 020.2 x64,使用的编程语言为Python。
分别选取面积较小的北京市、面积居中的河南省和面积较大的青海省作为目标区域,进行3组实验,具体任务信息如表 2所示。
|
|
表 2 任务信息表 Table 2 Table of task information |
为了验证本文算法的性能,将之与标准的CS和遗传算法(genetic algorithm,GA)做对比,在调用3种算法时,保证模型输入相同,即目标区域、选用卫星、成像规划时间、收敛条件相同,同时把对目标区域的覆盖率作为优化目标。
CS的主要参数为抛弃概率和种群规模,算法的发明者经过多组参数实验验证抛弃概率为0.25,种群规模在15~40之间时,收敛速度对参数选择并不敏感。因此,设置抛弃概率为0.25,种群规模为26。ICS中,取φ0为4,h0为200,此取值为多次实验得到的经验取值。作为对比算法,GA的种群规模与布谷鸟搜索算法保持一致,交叉概率、变异概率的取值是经过多次实验调参后的优选取值组合。算法中参数的取值如表 3所示。
|
|
表 3 算法参数表 Table 3 Algorithm parameters |
用3种算法分别对本文所建模型进行求解,设定迭代次数上限为400次,将各组实验分别独立进行10次,记录实验结果表 4所示。
|
|
表 4 不同区域目标实验结果对比 Table 4 Comparison of experimental results of different regional targets |
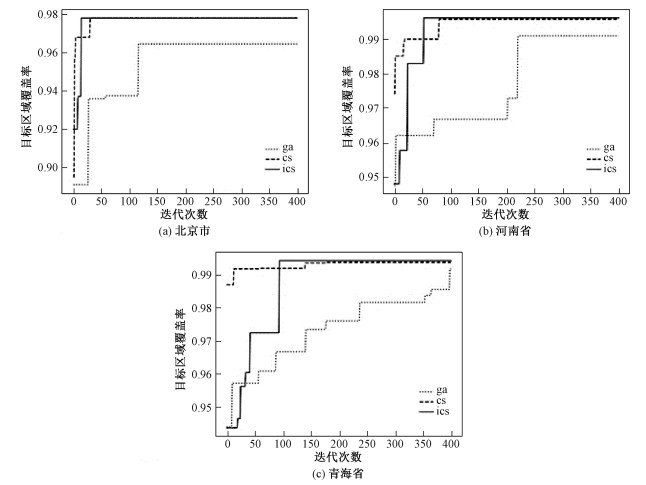
为更直观地将3种算法做对比,将实验的覆盖率变化图记录在图 5。
|
Download:
|
| 图 5 不同区域目标覆盖率变化图 Fig. 5 Changes in coverage rate of different regional targets | |
从目标函数值来看,当目标区域为北京市时,GA的平均覆盖率为97.11%,ICS和CS均可达到97.80%的覆盖率;以河南省为目标区域时,GA的平均覆盖率为99.10%,ICS和CS平均可达到99.60%及以上的覆盖率;以青海省为目标区域时,ICS的覆盖率为99.76%,相比于CS的99.69%和GA的98.78%,寻优效果也有提升。由此可见,对于不同规模的卫星成像规划问题,ICS的求解精度高于CS和GA。
从结果稳定性来看,在进行的3组实验中,ICS优化结果的标准差分别为GA的0%、28.57%、14.29%,CS优化结果的标准差分别为GA的0%、42.85%、14.29%。可见无论是ICS还是CS,其鲁棒性均强于GA,优化结果相对更稳定。
从收敛次数来看,在以北京市作为目标区域时,ICS的平均收敛次数是14次,少于CS和GA的平均收敛次数;目标区域为河南省时,问题规模、解空间增大,ICS的平均收敛次数仍小于CS和CA,且从覆盖率大小看,GA易陷入局部最优;当目标区域变为青海省时,ICS的平均收敛次数为156次,少于CS的平均收敛次数,而GA迭代400次未收敛。从收敛时间来看,当问题规模较小时,3种算法均可以在较短时间内达到收敛,ICS及CS的收敛时间比GA略长;随着问题规模的增大,3种算法的收敛时间都有所增加;而当问题规模进一步增大时,ICS和CS可以在一定时间内达到收敛,而GA未收敛。这是由于ICS和CS通过短距离的搜索与偶尔较长距离的行走相间的莱维飞行,使得算法的寻优性能更好。可见随着问题规模的增大,ICS和CS的寻优性能保持稳定,而GA易陷入局部最优,收敛性变差。对于大规模问题,IGA和GA的收敛性要优于CS。此外,在3组实验中,ICS的收敛时间均小于CS,这是由于引入的非线性惯性权重使得算法的寻优性能进一步增强,说明改进策略是有效的。
相比于GA,ICS和CS既提高了覆盖率,又提高了结果的稳定性,而且收敛性较好;相比于CS,在保证算法求解精度和稳定性的前提下,ICS缩短了收敛时间,考虑到研究问题的规划周期较长,本文采用算法的运行时间是可以接受的。总体而言,针对成像规划问题,采用ICS求解要优于CS和GA。
5 结语本文针对多卫星区域目标的成像规划问题,考虑卫星姿态、传感器使用和过境时间、成像时云量及光照等约束条件,建立约束满足模型,设计了布谷鸟搜索算法求解。为进一步提高求解效率,在算法搜索过程中引入非线性惯性权重,提出一种改进的布谷鸟搜索算法,加快了收敛速度。结果表明,与遗传算法和标准布谷鸟算法相比,改进布谷鸟搜索算法的目标完成率和稳定性有明显提高,卫星资源利用率得到了提高,验证了本文方法的有效性。
| [1] |
Bensana E, Verfaillie G, Agnèse J C, et al. Exact and inexact methods for the daily management of an earth observation satellite[DB/OL]. Proceedings of the Fourth International Symposium Space Mission Operations and Ground Data Systems-SpaceOps' 96, Munich, Germany, 1996[2021-03-04]. https://www.researchgate.net/publication/2765500_Exact_And_Inexact_Methods_For_The_Daily_Management_Of_An_Earth_Observation_Satellite.
|
| [2] |
贺仁杰. 成像侦察卫星调度问题研究[D]. 长沙: 国防科学技术大学, 2004.
|
| [3] |
Vasquez M, Hao J K. A "logic-constrained" knapsack formulation and a tabu algorithm for the daily photograph scheduling of an earth observation satellite[J]. Computational Optimization and Applications, 2001, 20(2): 137-157. |
| [4] |
Wolfe W J, Sorensen S E. Three scheduling algorithms applied to the earth observing systems domain[J]. Management Science, 2000, 46(1): 148-166. Doi:10.1287/mnsc.46.1.148.15134 |
| [5] |
白保存. 考虑任务合成的成像卫星调度模型与优化算法研究[D]. 长沙: 国防科学技术大学, 2008.
|
| [6] |
李志亮, 李小将, 孙伟. 考虑成像质量的敏捷卫星任务调度模型与算法[J]. 宇航学报, 2017, 38(6): 590-597. Doi:10.3873/j.issn.1000-1328.2017.06.005 |
| [7] |
李海玲, 党琦. 一种基于优先级的卫星成像任务快速规划流程[J]. 载人航天, 2018, 24(6): 821-826. Doi:10.16329/j.cnki.zrht.2018.06.017 |
| [8] |
明卫鹏, 马广彬, 章文毅. 基于基因表达式编程的多星成像任务规划算法[J]. 中国科学院大学学报, 2020, 37(4): 532-538. Doi:10.7523/j.issn.2095-6134.2020.04.013 |
| [9] |
申经伟. 基于改进布谷鸟算法的港口群海铁联运网络优化[D]. 大连: 大连海事大学, 2020.
|
| [10] |
徐杨丽, 叶春明. 布谷鸟算法求解置换流水车间调度问题[J]. 数学理论与应用, 2015, 35(3): 89-96. |
| [11] |
明波, 黄强, 王义民, 等. 基于改进布谷鸟算法的梯级水库优化调度研究[J]. 水利学报, 2015, 46(3): 341-349. Doi:10.13243/j.cnki.slxb.2015.03.011 |
| [12] |
邵萌, 李郁侠, 谭雅岚, 等. 基于布谷鸟搜索算法的变电站选址方法研究[J]. 电网与清洁能源, 2016, 32(11): 51-54, 61. Doi:10.3969/j.issn.1674-3814.2016.11.009 |
| [13] |
Yang X S, Deb S. Cuckoo search via lévy flights[C]//2009 World Congress on Nature & Biologically Inspired Computing (NaBIC). December 9-11, 2009, Coimbatore, India. IEEE, 2009: 210-214. DOI: 10.1109/NABIC.2009.5393690.
|
| [14] |
陈乐, 龙文. 求解工程结构优化问题的改进布谷鸟搜索算法[J]. 计算机应用研究, 2014, 31(3): 679-683. Doi:10.3969/j.issn.1001-3695.2014.03.009 |
| [15] |
Yang X S. Nature-Inspired Metaheuristic Algorithms[M]. 2nd ed. Frome, UK: Luniver Press, 2010: 129-139.
|
| [16] |
韩琼, 章文毅. 多星联合成像编程技术研究[J]. 遥感信息, 2013, 28(4): 19-23, 56. Doi:10.3969/j.issn.1000-3177.2013.04.004 |
| [17] |
王钧, 李军, 景宁, 等. 基于约束满足的多目标对地观测卫星成像调度[J]. 国防科技大学学报, 2007, 29(4): 66-71. Doi:10.10.3969/j.issn.1001-2486.2007.04.014 |
| [18] |
李军, 王钧, 陈健, 等. 基于多目标遗传算法的卫星成像任务调度技术[J]. 系统工程与电子技术, 2007, 29(7): 1164-1168. Doi:10.3321/j.issn:1001-506X.2007.07.034 |
| [19] |
刘延龙. 布谷鸟算法的应用研究及算法性能度量[D]. 哈尔滨: 东北林业大学, 2016.
|
 2023, Vol. 40
2023, Vol. 40 


