2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
卫星地面站资源调度问题是指根据卫星的任务应用需求,在有限的时间范围和特定的约束条件下,为卫星的数传、测控等任务配置相应的地面站资源(如天线、记录器等),得到满足卫星任务需求的资源分配调度方案。随着航天技术的发展,卫星任务数量也在急剧增多。巨大的任务量需要相应规模的卫星数传和测控运行体系,还需要合理地分配与调度地面站的设备资源,这样才能更好地完成卫星任务。其中任务运行设备的增加和改进受到经费、投入周期、工业技术等实际因素的制约,因此科学地安排和配置地面资源设备,对于地面站资源调度问题具有重要意义。
卫星任务的资源调度问题具有资源类型多、约束复杂、规模庞大、求解计算量大、评价体系复杂等特点[1],国内外许多学者对该问题进行过研究。经典的模型主要有约束满足模型(constraint satisfaction problem,CSP)[2]、0-1规划模型[3]、Petri网[4]、基于规则的调度模型[5]、混合整数规划模型[6]等;常用的调度方法主要有遗传算法及其改进算法[7]、启发式算法[6]等。目前已有的研究大多是根据不同卫星任务类型(如数传任务、测控任务)分别进行规划,随着运行体系的升级和发展,地面站资源(如天线)也不再是具有单一测控能力或单一数传能力的设备,而是逐渐升级为同时具有测控能力和数传能力的设备[8-9],因此可以考虑将不同类型的任务进行一体化规划,避免不同类型任务之间的资源冲突,统筹规划,共用资源,提高任务的完成率。
从运筹学的角度来讲,卫星地面站资源调度问题是一个具有优化目标、约束条件的优化问题。粒子群算法通过追踪粒子的个体最优和全局最优来搜索最优解[10],是一种参数简单、功能强大的群智能算法,目前已经广泛应用于优化问题[11-12]。最初粒子群算法用于解决连续的非整数问题,但是现实世界有很多问题是离散的整数问题,因此Kennedy和Eberhart[13]提出一种适用于离散问题的粒子群算法,可用于解决组合优化问题。如果将地面站的资源配置看作一个组合问题,则对于一般规模的调度场景,若使用穷举法,其产生的调度方案的数量规模是极其庞大的。粒子群算法的寻优机制可以使大规模的问题更快收敛至令人满意的解,因此本文利用粒子群算法对卫星任务的地面站资源调度问题进行求解。
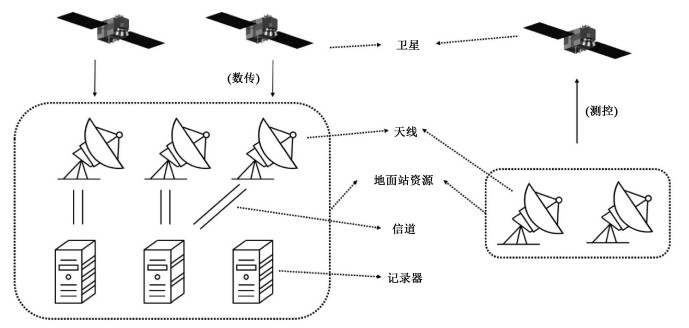
1 地面站资源一体化调度场景当卫星进入地面站接收圈时,称卫星在对于地面站的可视弧段内,此时卫星与地面站相互可见,可以相互通信。卫星将获取到的数据下传到地面站的过程是数传[14],数传过程中,地面站天线接收卫星数据,并由记录器记录;卫星测控是指通过测控设备对卫星飞行的轨道、姿态及卫星载荷进行测量、跟踪和控制[15],以保障卫星任务的完成,这一过程需要地面站天线向卫星发射信号,对卫星的有效载荷提出指令。图 1描述了卫星数传任务和测控任务的过程。
|
Download:
|
| 图 1 数传、测控过程及资源示意图 Fig. 1 Process of data transmission and TT&C | |
资源调度问题中,卫星的数传任务主要涉及的地面站资源有:地面站天线、信道与记录器。其中,信道是指数据传输与转换过程中的变频设备与解调设备,信道与天线和记录器之间通过开关矩阵连接。一般情况下,信道以共享网络化的方式管理,从理论上说,一个数传任务只要安排了天线,就一定有相应的信道配合安排,因此本文数传任务只考虑天线与记录器的调度情况。而测控任务中基带、频点等约束都体现在天线能力上,因此测控任务的资源调度问题只考虑天线这一种地面站资源。
卫星的数传任务和测控任务的资源调度有一定的区别,也有一定的共性,即任务类型与设备能力相匹配。数传和测控任务需要不同能力的天线来完成,一般来说,卫星的任务类型有以下3种:单一数传、单一测控、数传与测控任务。相应地,按照能力划分,天线也有3种:数传天线、测控天线、数传与测控天线。其中,数传与测控天线既可以执行数传与测控任务,也可以执行单一数传、单一测控任务;数传天线可以执行单一的数传任务;测控天线可以执行单一的测控任务。另外,数传与测控任务也可同时用一部数传天线和一部测控天线来完成,但这不符合一体化规划中资源设备的合理使用,因此一般情况下不考虑这种调度方式。
2 地面站资源调度问题建模为卫星任务的地面站资源调度问题建立约束满足模型,首先应对该问题的变量进行描述,再分析该问题的优化目标、约束条件。
地面站资源调度问题涉及的变量有以下5种:
1) 卫星任务集合J={ j1, j2, j3, …, ji, …, jn};
2) 地面站集合G={ g1, g2, g3, …, gq, …, gm};
3) 卫星集合S={ s1, s2, s3, …, sp, …, sz},任务ji的卫星用Sji表示;
4) 天线集合A={ a1, a2, a3, …, ak, …, ax},任务ji所用天线用Aji表示;
5) 记录器集合R={ r1, r2, r3, …, rl, …, ry},任务ji所用记录器用Rji表示。
2.1 优化目标卫星任务的地面站资源调度主要是为卫星任务安排地面站设备,根据实际调度场景,该问题往往是一个多目标的优化问题。针对卫星任务的资源调度问题主要设计如下优化目标:
1) 任务执行率最大
用Cji表示任务ji是否执行,若任务ji安排了符合约束的设备,那么Cji=1,否则Cji=0。
| $ \max {f_1} = \frac{{\sum _{i = 1}^{i = n} {{C_{{j_i}}}} }}{n}. $ | (1) |
2) 调度方案中所有任务的总弧长最大
| $ {\rm{S}}{{\rm{T}}_{{j_i}}} = \min \left( {{\rm{FS}}{{\rm{S}}_{{j_i}}}, {\rm{FC}}{{\rm{S}}_{{j_i}}}} \right). $ | (2) |
| $ {\rm{E}}{{\rm{T}}_{{j_i}}} = \max \left( {{\rm{FS}}{{\rm{E}}_{{j_i}}}, {\rm{FC}}{{\rm{E}}_{{j_i}}}} \right). $ | (3) |
| $ \max {f_2} = \sum\limits_{i = 1}^{i = n} {\left( {{\rm{E}}{{\rm{T}}_{{j_i}}} - {\rm{S}}{{\rm{T}}_{{j_i}}}} \right)} . $ | (4) |
式(2)~式(4) 中:FSSji、FCSji、FSEji、FCEji分别表示任务的实际数传开始时间、实际测控开始时间、实际数传结束时间、实际测控结束时间,f2表示调度方案的总任务弧长。
3) 尽量为任务安排其优选设备
| $ \begin{array}{c} \max {f_3} = \sum\limits_{i = 1}^{i = n} {\left( {\left( {{\rm{E}}{{\rm{T}}_{{j_i}}} - {\rm{S}}{{\rm{T}}_{{j_i}}}} \right) \times \left( {1/{\rm{SA}}\left( {{S_{{j_i}}}, {A_{{j_i}}}} \right)} \right) + } \right.} \\ \left. {\left( {{\rm{FS}}{{\rm{E}}_{{j_i}}} - {\rm{FS}}{{\rm{S}}_{{j_i}}}} \right) \times \left( {1/{\rm{SR}}\left( {{S_{{j_i}}}, {R_{{j_i}}}} \right)} \right)} \right). \end{array} $ | (5) |
f3表示调度方案每个任务的实际时长与其设备首选程度的乘积,其值越大,代表调度方案的设备越优选。其中,SA(Sji, Aji)表示任务ji的卫星对其天线的首选性值,SR(Sji, Rji)
表示任务ji的卫星对其记录器的首选性值。由于设备首选性数值与其首选程度呈负相关,因此,对设备首选性数值取倒数表示设备的首选程度。
2.2 约束条件 2.2.1 任务重要性约束按照优先级由高到低地执行卫星数传与测控任务:根据任务的紧急程度和重要程度,任务具有不同的优先级,在资源调度过程中,应先安排紧急、重要的任务。
2.2.2 地面站资源约束本文考虑天线和记录器两种设备资源,以下按照设备的能力约束、时间占用约束及天线记录器关联约束分别进行叙述。
1) 设备能力约束
① 天线对卫星可用
| $ {\rm{SA}}\left( {{S_{{j_i}}}, {A_{{j_i}}}} \right) \ne - 1. $ | (6) |
② 天线能力与任务类型相匹配
即任务ji的天线Aji的能力ATAji要满足任务类型Tji。
③ 记录器对任务可用
| $ {\rm{SR}}\left( {{S_{{j_i}}}, {R_{{j_i}}}} \right) \ne - 1. $ | (7) |
④ 只对含有数传的任务安排记录器
即如果任务ji的类型Tji为单一测控任务,就不需要对该任务安排记录器。
⑤ 记录器的逻辑记录器的个数LCRji满足卫星任务下行通道数SCji
| $ {\rm{S}}{{\rm{C}}_{{j_i}}} \le {\rm{L}}{{\rm{C}}_{{R_{{j_i}}}}}. $ | (8) |
⑥ 记录器的每个逻辑码速率LVRji满足卫星任务每个通道的下行码速率SVji
| $ \max \left( {{\rm{S}}{{\rm{V}}_{{j_i}}}} \right) \le {{\mathop{\rm LV}\nolimits} _{{R_{{j_i}}}}}. $ | (9) |
⑦ 记录器物理码速率PVRji满足卫星任务的最大码速率:
| $ {\mathop{\rm sum}\nolimits} \left( {{\rm{S}}{{\rm{V}}_{{j_i}}}} \right) \le {\rm{P}}{{\rm{V}}_{{R_{{j_i}}}}}{\rm{. }} $ | (10) |
2) 设备时间占用约束
① 某一时刻,一部天线只能安排一颗卫星的任务:即在[STji, ETji]时间段内,卫星任务ji的天线Aji不能被其他任务所用。
② 当一部天线完成一个任务,需要一定的切换时间t才能供下一任务使用:
即在[ETji, ETji +t]时间段内,卫星任务ji的天线Aji不能被其他卫星利用。
③ 在满足负载(即逻辑记录器个数、逻辑码速率、物理码速率)的情况下,记录器可以给多个任务共用。然而多个数传任务共用记录器执行任务不稳定,因此在资源充足的情况下,多个任务不共用记录器。当现有的记录器资源无法满足当前任务单独使用时,才考虑多任务共用记录器。
当记录器资源充足时,[FSSji, FSEji]时间段内,卫星任务ji的记录器Rji不能被其他任务所用。当记录器资源不足时,考虑[FSTji, FSEji]时间内记录器的剩余逻辑记录器个数、逻辑码速率、剩余物理码速率情况,如能满足当前任务需要,则可安排该记录器。
④ 当一个记录器完成一个任务,需要一定的切换时间t1,才能供下一任务使用:
即在[FSEji, FSEji+t1]时间段内,卫星任务ji的记录器Rji正在占用的通道不可被其他卫星利用。
3) 天线记录器关联约束
单一测控任务只需要安排天线资源。对于含有数传的任务,只安排天线或只安排记录器的任务无效。
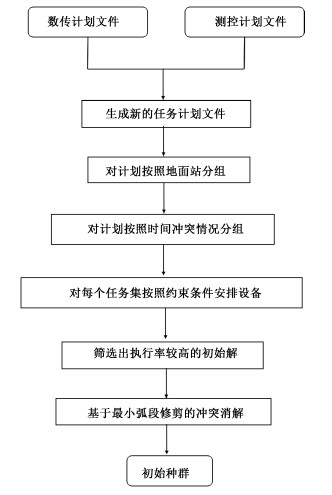
3 结合启发式规则的改进粒子群算法 3.1 生成初始种群卫星任务的地面站资源调度问题具有约束复杂、规模较大等特点,因此利用分治思想对问题进行分解,即将任务按照设备、时间分成互不关联的多个集合,可以有效避免计算过程中对无关部分的遍历,减少问题的时间复杂度。卫星任务的地面站资源调度问题是一个多目标的优化问题,对于优化目标1)任务执行率最大和优化目标2)任务总时长最大来说,其进化范围是很有限的。如果通过算法进行进化或搜索,不仅会增加计算的时间成本,效果也并不明显,因此考虑先随机生成一定数量的初始解,再按照优化目标1)和优化目标2)对其进行筛选,用较优的初始种群参与算法的进化与搜索。生成初始种群的流程如图 2所示。
|
Download:
|
| 图 2 生成初始解流程图 Fig. 2 Flow chart of initial solution generation | |
在获取要输入的任务计划文件后,对任务分组,同一集合的任务属于同一地面站,任务之间存在时间冲突,不同的冲突任务集合之间资源调度互不关联,对每一组分别进行约束和求解。
由于算法的初始解是随机生成的,为了减少迭代过程中的计算次数,可以根据优化目标1)和2)的目标函数值对初始解进行初步筛选,选出较优的初始解对优化目标3)进化。先随机生成M个初始解,计算每个初始解的任务执行率,选出执行率最高的前N(N < M)个初始解。
针对每一个冲突任务集合,当组内发生不可调节的设备资源使用冲突时,还要对任务时间进行合理的弧段修剪,尽量给每个任务都安排设备。对于那些因为资源冲突未安排设备的任务,按照以下原则进行弧段修剪来消解冲突:
1) 只对遥感成像卫星的数传任务进行修剪。对于其他任务,不完整执行很可能导致任务失败,因此并不是对所有任务都可以进行弧段修剪。
2) 只修剪普通优先级的任务,要保证重要任务和紧急任务的完整执行。
3) 弧段修剪后的剩余数传时间不得小于t2。数传时间过短的任务无效。
4) 根据任务总时长最大的优化目标,为了最大化整体任务时长,如有多种可以消解冲突的修剪方案,选择修剪时间最短的方案。
5) 除任务时间被其他任务几乎完全覆盖的任务,保证所有任务都安排了设备。
3.2 改进粒子群算法粒子群算法是一种进化算法,从初始解出发,通过迭代寻求最优解。本文提及的优化目标1)、2)已经在生成初始解步骤进行了筛选,粒子群算法对优化目标3)进行优化。输入为经过筛选的N个较优初始解,进化的决策变量为天线Aji和记录器Rji。传统的粒子群算法流程如下:
1) 输入N个粒子组成的初始解,初始化粒子群:确定种群位置pop[i]、速度Vel[i]。
2) 计算每个粒子的适应度值。
3) 找到粒子的个体历史最优Pbest,找到粒子的全局历史最优Gbest。
4) 按照以下公式更新粒子的位置:
| $ \begin{array}{c} {\mathop{\rm Vel}\nolimits} [i] = {\mathop{\rm Vel}\nolimits} [i] + {r_1} \times {c_1} \times \left( {{P_{{\rm{best }}}} - {\mathop{\rm pop}\nolimits} [i]} \right) + \\ {r_2} \times {c_2} \times \left( {{G_{{\rm{best }}}} - {\mathop{\rm pop}\nolimits} [i]} \right){\rm{. }}\\ {\mathop{\rm pop}\nolimits} [i] = {\mathop{\rm Vel}\nolimits} [i] + {\mathop{\rm pop}\nolimits} [i]. \end{array} $ |
其中: r1、r2是0与1之间的随机数,c1、c2是学习因子参数,通常取2。粒子通过本身的经验和整个种群的经验来决定下一步的进化方向。本文中,由于卫星任务地面站资源调度问题是一个离散的整数问题,因此对速度进化公式的计算值进行取整,再更新粒子的位置。
5) 判断更新后的粒子是否满足约束条件: 如满足,则进化成功;否则,退回原位置不动。
6) 若未达到终止条件重复步骤2)~6),否则结束,输出全局最优值。
传统粒子群算法中,每次迭代进化后判断粒子是否符合约束。只有符合约束的粒子进化了,不符合约束的没有进化,这极大限制了粒子群算法的搜索空间,使其陷入局部最优。因此,对于那些进化后不符合约束的粒子,利用启发式规则对其进行修正,使其变成符合约束的粒子,这种做法可以有效扩大解空间,寻得更好的解。根据卫星任务资源调度的约束条件,定义以下启发式规则:
1) 对于每个种群中与其他任何任务都无时间冲突的任务,直接安排其最优选设备。
2) 如进化后的任务不符合设备时间占用约束,则搜索其冲突集合中与该任务有设备占用冲突的任务,为这些冲突任务更换满足约束的设备。
3) 更换设备时,优先更换比当前设备更优选的设备,如不满足约束,再考虑更换次优选的设备。
结合启发式规则的改进粒子群算法流程如图 3所示。

|
Download:
|
| 图 3 结合启发式规则的改进粒子群算法流程图 Fig. 3 Flow chart of modified PSO combined with heuristic methods | |
为了验证算法的有效性,本文从2020年中国遥感卫星地面站受理的任务中随机选取真实任务案例进行资源调度算法仿真实验。案例的任务规模与地面资源情况见表 1、表 2(已隐去真实信息,用代号表示)。
|
|
表 1 任务规模 Table 1 Size of tasks |
|
|
表 2 地面站资源情况 Table 2 Resources of ground station |
在卫星任务地面站资源调度问题中,常规算法有遗传算法等,本文将通过仿真实验对比遗传算法、粒子群算法和结合启发式规则的改进粒子群算法。由于遗传算法、粒子群算法均带有一定随机性,为排除实验偶然性,分别利用遗传算法、传统粒子群算法(以下简称粒子群算法)、结合启发式规则的改进粒子群算法(以下简称改进算法)对每个案例做10次实验。实验经验表明,遗传算法在经过500次迭代可以取得较满意的解,粒子群算法在经过100次以内的迭代几乎均可以收敛。计算每个案例10次实验的目标函数平均值和平均差,实验结果如表 3所示。
|
|
表 3 各算法实验结果比较 Table 3 Comparison of the results of algorithms |
为合理评价算法,本文通过算法运行时间、收敛代数、目标函数值、目标函数值的平均差来评价算法的效率、收敛速度、寻优能力和算法稳定性。
寻优性能方面,通过实验结果可以看出,通过对初始解进行筛选,可以有效保证调度方案的任务执行率。在实验案例中,除了有时间被包含的任务的案例(如案例3),所有案例的任务执行率达到100%。也就是说,绝大部分调度方案都可以合理配置资源,有效避免了不科学地舍弃任务。其中,案例1任务完整执行,即没有舍弃任何接收弧段;执行任务总弧长超过计划总时长的99%,即因资源不足而减少的任务时长很少。优化目标3)为卫星任务尽量安排其最佳设备,是通过遗传算法、粒子群算法优化得到的。实验结果表明,相对于遗传算法,粒子群算法得到的调度方案寻优能力提高33.13%,改进粒子群算法的寻优能力较遗传算法提高42.74%,相对于传统粒子群算法,结合启发式规则的改进粒子群算法寻优能力提高6.67%。
从运行时间来看,算法的运行时间受到迭代次数、约束计算次数的影响,遗传算法主要通过交叉、变异来寻优,它的计算约束次数较少;而粒子群算法每进化一次都要计算约束。虽然改进粒子群算法中增加了对启发式规则的判断,但相比传统算法,改进粒子群算法减少了对无冲突任务的遍历,因此改进算法并没有增加较多的运行时间,很多案例中,改进算法甚至还加快了算法的运行速度。
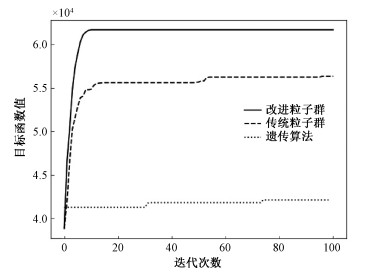
从算法达到收敛时的迭代次数来看,遗传算法的收敛代数最多,在多次实验中,遗传算法都表现出较慢的收敛速度。粒子群算法都是迭代100次,其中改进的粒子群算法相对于传统粒子群算法收敛速度平均提高48.11%,即改进算法具有更快的收敛速度(如图 4所示)。
|
Download:
|
| 图 4 某一地面站任务各算法收敛速度对比 Fig. 4 Comparison of convergence rate of a certain station | |
从各案例10次实验的平均差来看,遗传算法的稳定性要优于粒子群算法,这与遗传算法的寻优能力和进化程度较弱有关。经改进的粒子群算法相对于传统粒子群算法稳定性平均提高53.12%,相对于遗传算法稳定性提高43.5%。即改进算法具有更好的稳定性(如图 5所示)。

|
Download:
|
| 图 5 改进算法与传统算法稳定性对比 Fig. 5 Comparison of stability between improved algorithm and traditional algorithm | |
卫星任务地面站资源调度问题具有任务规模大、资源有限、约束复杂、求解难度大等特点,本文通过分析资源调度问题的优化目标和卫星任务与地面资源的约束,为卫星任务地面站资源调度问题建立约束满足模型。先通过一定的规则对任务集合进行分解,再对初始解进行筛选,用选出的高质量初始解参与粒子群进化,通过与常规调度方法(如遗传算法)对比,证明了粒子群算法对卫星任务资源调度问题的可行性,并提出一种结合启发式规则的改进粒子群算法。仿真实验表明,结合启发式方法的改进粒子群算法为卫星任务的地面站资源调度问题提供了设备更优选的方案,并有效提高了传统粒子群算法的收敛速度和稳定性。
| [1] |
金光. 卫星地面站测控资源调度CSP模型[J]. 系统工程与电子技术, 2007, 29(7): 1117-1120. Doi:10.3321/j.issn:1001-506X.2007.07.024 |
| [2] |
贺仁杰, 谭跃进. 基于约束满足的卫星地面站资源优化分配问题研究[J]. 计算机工程与应用, 2004, 40(18): 229-232. Doi:10.3321/j.issn:1002-8331.2004.18.072 |
| [3] |
金光, 武小悦, 高卫斌. 卫星地面站资源调度优化模型及启发式算法[J]. 系统工程与电子技术, 2004, 26(12): 1839-1841, 1875. Doi:10.3321/j.issn:1001-506X.2004.12.026 |
| [4] |
王远振, 赵坚, 聂成. 多卫星-地面站系统的Petri网模型研究[J]. 空军工程大学学报(自然科学版), 2003, 4(2): 7-11. Doi:10.3969/j.issn.1009-3516.2003.02.002 |
| [5] |
Schaire S, Altunc S, Malphrus B K, et al. NASA Wallops flight facility-morehead state ground network for small satellite mission operations[C]//SpaceOps 2014 Conference. 5-9 May 2014, Pasadena, CA. Reston, Virginia: AIAA, 2014. DOI: 10.2514/6.2014-1635.
|
| [6] |
Gooley T D, Borsi J J, Moore J T. Automating air force satellite control network (AFSCN) scheduling[J]. Mathematical and Computer Modelling, 1996, 24(2): 91-101. Doi:10.1016/0895-7177(96)00093-3 |
| [7] |
张鹏, 冯旭祥, 葛小青. 基于改进遗传算法的多天线地面站硬件资源分配方法[J]. 计算机工程与科学, 2017, 39(6): 1155-1163. Doi:10.3969/j.issn.1007-130X.2017.06.020 |
| [8] |
秦玉峰, 聂少军, 赵鸿, 等. 基于高级在轨系统的测控数传一体化方案[J]. 飞行器测控学报, 2016, 35(5): 409-414. Doi:10.7642/j.issn.1674-5620.2016-05-0409-06 |
| [9] |
于志坚, 丁溯泉, 罗伦. 航天测控与数传接收综合信道构想[J]. 遥测遥控, 2002, 23(4): 8-11. |
| [10] |
Kennedy J, Eberhart R. Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks. November 27-December 1, 1995, Perth, WA, Australia. IEEE, 1995: 1942-1948. DOI: 10.1109/ICNN.1995.488968.
|
| [11] |
李爱国, 覃征, 鲍复民, 等. 粒子群优化算法[J]. 计算机工程与应用, 2002, 38(21): 1-3, 17. Doi:10.3321/j.issn:1002-8331.2002.21.001 |
| [12] |
杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004, 6(5): 87-94. |
| [13] |
Kennedy J, Eberhart R C. A discrete binary version of the particle swarm algorithm[C]//1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational, Cybernetics and Simulation. October 12-25, 1997, Orlando, FL, USA. IEEE, 1997: 4104-4108. DOI: 10.1109/ICSMS.1997.637339.
|
| [14] |
常飞. 卫星地面站数传资源配置优化模型与算法研究[D]. 长沙: 国防科学技术大学, 2010.
|
| [15] |
唐旻. 卫星系统数传与测控服务策略研究[D]. 长沙: 国防科学技术大学, 2013.
|
 2022, Vol. 39
2022, Vol. 39 


