2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
合成孔径雷达(synthetic aperture radar, SAR)是一种主动式微波遥感系统[1]。1951年, 美国研究人员首先提出SAR的概念, 60年代之后各种星载或机载SAR被相继研制和推出[2]。1979年, 中国的第一幅SAR图像由中国科学院电子学研究所得到。在这之后, 国内对于SAR的研究逐渐深入, 取得了长足的发展。SAR不受光照条件、气候和一些其他环境因素的限制, 可以满足更多实际的需求, 同时SAR可以获取更丰富的目标信息, 因此在对地观测任务上相较于传统光学遥感器更具优势, 这也使得SAR在各个领域的应用越来越广泛[3]。
与传统SAR系统固定的收发方式相比, 极化SAR系统可以同时获取同一目标在不同极化脉冲下的散射特征, 地物反射回来的微波经过系统检测后得到极化散射矩阵, 该矩阵涵盖了丰富的极化散射信息。但极化SAR在提供丰富散射信息的同时也增加了数据的复杂度, 丰富多样的极化散射特征也使地物信息的准确提取和处理更为困难[4]。
极化SAR所含有的丰富的地物信息, 使得极化SAR智能解译逐渐引起国内外研究人员的关注。极化SAR地物分类是极化SAR智能解译中非常重要的一环, 它通过提取丰富的极化SAR特征来获取像素的地物标签从而实现像素级的分类任务。极化SAR地物分类先进行特征的提取, 获得更有效的地物目标的信息, 然后利用提取到的特征进行分类。随着SAR智能解译的不断发展, 基于随机森林[5]、贝叶斯方法、支持向量机、神经网络等分类算法被应用于SAR图像分类。Demirhan和Salor[6]使用改进的径向基函数进行特征提取而后送入SVM中进行分类。Hou等[7]使用基于分解特征的超像素方法克服了斑点噪声。上述基于机器学习的方法需要进行特征工程, 如通过极化目标分解等方法提取特征后再调用算法。而这类特征通常需要根据具体问题进行具体设计, 对先验知识的依赖程度较高, 对不同数据、不同地物目标的适应性较差, 表征能力往往不尽如人意。因此, 如何使提取的特征更具泛化性引起了学者的广泛关注。
近年来, 神经网络在模式识别的各个领域取得了较好的成果。神经网络具有从大量数据中以分层的方式自主学习特征表示的能力, 而不需要基于领域特定知识设计手工特征[8], 这为极化SAR地物分类提供了新的手段。Chen等[9]通过多层字典对和自编码器提取特征, 使提取的特征更加抽象。Liu等[10]提出一种邻域保留神经网络模型用于极化SAR分类, 通过联合加权策略保留像素的空间依赖性。Zhu等[11]创新性地提出基于目标像素灰度下降的图卷积神经网络来对地物进行分类。Zhang等[12]提出复数CNN模型, 以直接适用于极化SAR数据的复数, 并在极化SAR分类中取得很好的效果。但是, 基于神经网络的地物分类方法也存在一个问题:为了学习到更好的表示, 神经网络通过增加网络维度构建高维特征空间用于地物分类, 但高维特征往往包含大量冗余信息并互相干扰, 使得分类边界不明确, 从而导致训练难度增加和分类精度下降。
针对上述问题, 从传统的提取极化特征的极化目标分解的思想出发, 本文提出一种基于图像分割和EM算法的低秩重构网络(low-rank-reconstruction-net, LRR-Net)。LRR-Net首先通过一段卷积神经网络提取高维特征图, 而后通过EM算法得到一组具有以下特点的基:每个基都可以反映某一类地物的特征, 最大程度地还原信息; 数量要少, 基之间互不相似, 不会包含冗余信息。通过这组基对高维特征进行一个低秩重构, 使得高维空间中的特征重新嵌入到低维空间上, 而后利用重构的信息进行像素级的图像分割。低秩重构网络LRR-Net不仅仅适用于全极化SAR图像的地物分类, 对于非全极化的SAR图像以及光学遥感图像的地物分类同样适用, 具有普适性。本文基于高分三号全极化数据进行实验, 实验结果表明, 在保证分类精度的前提下, 参数量显著减少。
1 方法 1.1 极化目标分解极化SAR图像因其含有地物目标物理散射机理的信息, 不同地物目标的极化散射特性存在差异。对于全极化图像, 其丰富的极化散射特征就是通过极化目标分解方法提取到的。极化目标分解理论的主要思想是将一个散射矩阵分解成几个能反映不同散射机制的矩阵的线性组合, 而不同地物在极化散射特性存在差异, 在不同散射机制下的分量大小不同, 从而达到区分地物的目的。如Pauli基是一组完备正交基, 在互易的条件下可以表示为
| ${\left[S_a\right]=\frac{1}{\sqrt{2}}\left[\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right], \left[S_b\right]=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1 & 0 \\ 0 & -1\end{array}\right] }$ ${\left[S_c\right]=\frac{1}{\sqrt{2}}\left[\begin{array}{ll}0 & 1 \\ 1 & 0\end{array}\right] }$ | (1) |
以上分别代表奇次散射、偶次散射、π/4偶次散射的散射机制, 利用在Pauli基下的散射能量大小即可进行分类识别。从图 1可以看出, 经过Pauli分解后生成的伪彩色图可以很清晰地区分不同地物目标。

|
Download:
|
| 图 1 Pauli伪彩色图 Fig. 1 Pauli pseudo-color image | |
受此启发, 神经网络在高维的特征存在信息冗余, 如果通过类似极化目标分解的方法对高维信息降维得出一组基, 再利用这组基对高维信息进行重构。那么重构后的高维信息的分类边界会更加清晰, 不需要再去堆叠卷积层进行信息提纯, 从而可以大大降低神经网络的计算量。极化目标分解是已知几种散射机制, 可以直接通过计算得到不同散射机制下的分量大小, 但输入图像通过卷积神经网络提取到特征图后, 已知的只有每个像素的高维特征, 想要对高维特征进行低秩重构, 基和在每个基下的分量大小都是需要求解的变量。对于这种含有隐变量的模型参数求解, 可以采用EM算法的思想。具体地, 本文采用类似求解K-means的方法来求解低秩重构模块的模型参数。
1.2 EM算法EM算法是一种迭代优化策略, 是一种启发式的迭代方法。最初是为了解决数据缺失情况下的参数缺失问题, 即通过迭代完成对隐变量模型的参数估计[13]。其计算方法是每一次迭代都分为2步, 第1步为E-step, 根据样本, 估计出隐变量的值, 即样本属于每个分布的概率; 第2步为M-step, 依据上一步估计出的隐变量利用最大似然求解模型参数, 然后反复迭代, 直至最后收敛。
如果优化目标是非凸的, EM算法的特性可以使优化目标收敛到一个局部最优解, 而当优化目标是凸的时候, EM算法可以保证收敛到全局最优解, 这点同梯度下降法相同。
K-means算法是EM算法的一个特例。K-means问题的目的是要将样本{ x1, x2, ……, xn }分成K个簇, 这里的隐变量就是每个样本所属的类别, 而模型的参数为K个质心。按照EM算法的流程, 首先初始化K个质心为μ1, μ2, ……, μk, 之后进行E-step, 依据当前质心计算每个样本属于哪个簇:
| $\boldsymbol{z}_n=\operatorname{argmin}\left\|\boldsymbol{x}_n-\boldsymbol{\mu}_k\right\|^2 .$ | (2) |
M-step:根据分类后的样本重新计算每个簇的质心:
| $\boldsymbol{\mu}_k=\frac{\boldsymbol{\sum}_{n=1}^N\left\{\boldsymbol{z}_n=k\right\} \boldsymbol{x}_n}{\boldsymbol{\sum}_{n=1}^N\left\{\boldsymbol{z}_n=k\right\}} ;$ | (3) |
重复计算E-step和M-step直至收敛。
1.3 低秩重构模块在神经网络中, 假定输入的特征图为
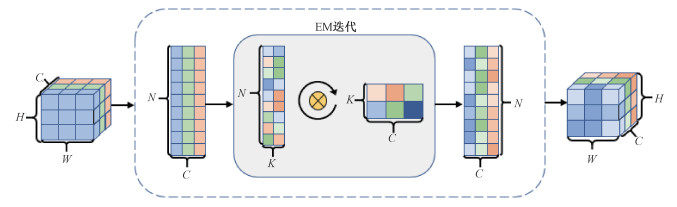
|
Download:
|
| 图 2 低秩重构模块 Fig. 2 Low-rank reconstruction unit | |
特征图进入低秩重构模块先进行变换, 把像素个数记为N=H×W, 特征图变为
|
|
表 1 低秩重构模块 Table 1 Low-rank reconstruction unit |
核函数ψ(x n, μ k)这里有多种选择, 如内积、欧氏距离、RBF核等, 在实验中发现[14], 核函数的选择对结果影响不大, 这里选用指数内积exp(a T b), 那么隐变量Z可以表示为 X与μ的内积外加一个Softmax层:
| $Z=\operatorname{Softmax}(\boldsymbol{X} \cdot \boldsymbol{\mu}) .$ | (4) |
同样地, 仿照K-means算法求μ的方法, μ为X在隐变量Z上的加权平均。重构后的XO, 特征图之间表示同类地物的差距变小, 而表示不同类的差距变大。即经过重构后的特征图, 虽然大小仍为N×C, 但是信息纯度更高, 每张图的语义信息相较之前更加丰富, 不再需要堆叠更多的卷积层去学习更深层的信息即可对地物进行有效的区分。换句话说, 低秩重构模块在不增加参数运算量的情况下完成了卷积层提取深度特征的作用。同时, 低秩重构模块用整张图全局信息来做EM迭代的, 可以直接捕捉远程依赖, 相当于一个全图尺寸的卷积核, 与卷积层的局部感受野相比更具优势。
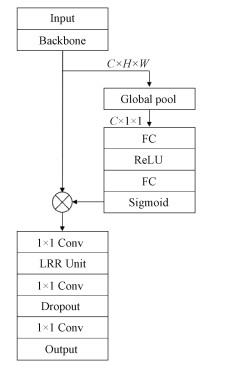
1.4 网络框架LRR-Net的整体框架如图 3所示, 全极化图像经过预处理之后, 首先经过一个卷积神经网络作为用于提取特征图, 利用卷积神经网络的特性, 提取深层特征并映射特征到高维空间, 本文使用的backbone是Resnet[15]。
|
Download:
|
| 图 3 低秩重构网络 Fig. 3 Low-rank reconstruction net | |
第二步特征图经过通道注意力模块[16]。特征图首先通过全局平均池化来来压缩空间信息, 每个通道获得一个值, 之后经过全连接层和非线性层融合各个特征图的信息, 学习通道之间的联系。第1个全连接层是把C个通道压缩, 来降低计算量, 再第2个全连接层恢复回C个通道。最后经过Sigmoid获取到每个通道的权重, 通过乘法逐通道地加权到先前的特征图, 完成对特征重分布。通道注意力模块可以让神经网络捕获通道之间的关系, 获得每个通道维度的重要性, 改变全局的数值分布从而让低秩重构模块更好地收敛。
之后经过一个不含ReLU激活函数的1×1卷积层。ReLU激活函数
| $\operatorname{ReLU}=\left\{\begin{array}{l}0, \text { if } x<0, \\ x, \text { if } x \geqslant 0\end{array}\right.$ | (5) |
这里不含ReLU激活函数的原因是为了让参数取值范围回到负无穷到正无穷的范围。如果不加这一层, 基的取值范围也会因为ReLU的值域在正区间被限制, 与卷积层的参数相比丧失了一半的表征能力。
之后经过低秩重构模块, 经过几次迭代后参数收敛得到重构后的特征图, 实现特征从的重构。同时为了减少过拟合, 加入了按通道随机丢弃的二维Dropout, 提升网络的稳定性。最后一个1×1卷积层用来将维度缩减到与类别数量相同以便后续计算损失函数进行网络参数更新。
2 实验与分析 2.1 数据本文采用的极化SAR数据集来自中国的高分三号卫星。高分三号于2016年8月10日发射成功, 2017年1月23日正式投入使用。中国首颗分辨率达到1 m的C频段多极化合成孔径雷达卫星, 是高分专项“天眼工程”中唯一一颗“雷达星”[17]。
为了对模型进行训练与测试, 本文利用带人工标注标签的QPSI全极化波段的杭州地区的数据集, 除去背景之外, 标签共有6类, 分别为:水体, 建筑物, 工业区, 林草地, 土地&裸地, 其他。在此之前极化SAR的数据集如AIRSAR的L波段的旧金山地区数据或Flevoland地区数据, 这类数据往往只有一张标注的图片, 数据量的稀缺使得神经网络较传统方法并没有太大优势, 且极容易过拟合, 在一些论文中已经可以达到99 % 左右的准确率。而该数据集共有500×4张全极化图像, 每张图像的大小为512像素×512像素, 可以很好地验证不同神经网络图像分割方法的有效性, 避免了数据稀缺带来的影响, 相较其他数据集更具说服力。每张图片的标签均是人工标注, 可信度较高。每个样本包含4个通道的图像以及人工标注的真值图片, 如图 4所示。

|
Download:
|
| 图 4 SAR原始图像以及真值标注 Fig. 4 SAR image and ground truth | |
为验证本文方法的有效性, 将LRR-Net的地物分类结果与图像分割的经典模型FCN[18]以及近几年的典型模型PSPNet[19]和DeeplabV3[20]模型比较。FCN是语义分割的基本框架, 后续的算法都是在这个基础上改进而来。PSPNet通过加入金字塔模块聚合基于不同区域的上下文信息, 这也成为了后续很多网络的基本模块。DeeplabV3加入了多尺度空洞卷积的模块, 最大程度地减少了信息的丢失。以上几个网络的思想都在图像分割领域产生了重大影响, 将结果与它们作比较具有较高的说服力。同时, 为保持变量的统一性, PSPNet、DeepLabV3和LRR-Net使用的基础特征提取网络均为Resnet50。神经网络的计算量复杂度一般使用FLOPs或MACC来衡量。FLOPs全称为floating point operations, 即浮点运算数, 而MACC全称为multiply-accumulate operations, 即乘加运算数。MACC会把一次浮点乘法和一次浮点加法当做一次运算, 因此一般来说FLOPs是MACC的2倍, 本文使用MACC来评估模型复杂度。当输入图像大小为512×512时, PSPNet的计算量复杂度为184 G MACC, DeeplabV3的计算量复杂度为171 G MACC, FCN的计算量复杂度为160 G MACC而LRR-Net的计算量复杂度仅为137 G MACC, 大大减少了神经网络运算的复杂度, 这也是LRR-Net特性的体现。
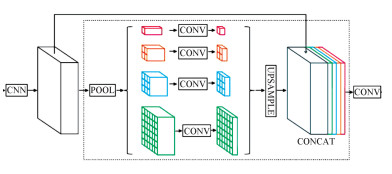
PSPNet在backbone之后链接了多尺度感受野的金字塔结构来提取更具语义的特征从而提升分割精度, 如图 5所示。多尺度的融合虽然对分割精度的提升有效, 但每个尺度都会增加一倍的计算量, 融合之后的特征图维度更是高达2 048维。同样地, DeeplabV3计算复杂度的增加主要是使用了多尺度的空洞卷积堆叠卷积层来获取更多特征。而LRR-Net中, 特征图经过低秩重构模块之后每张图的类内差距变小而类间差距变大, 等于完成了深层特征提取, 因此不需要后面连接更多卷积层, 大大降低复杂度。
|
Download:
|
| 图 5 PSPNet结构 Fig. 5 Structure of PSPNet | |
本文利用高分三号QPSI全极化波段进行实验, 输入图像的位置为30.3°N, 120.4°E。经过预处理后裁剪成500张长和宽都为512像素的图像, 真实地物标签分为6类, 分别为水体, 建筑物, 工业区, 林草地, 土地 & 裸地, 以及其他。本文按照4∶1的比例随机划分训练集和测试集, 经过对输入数据的归一化等预处理之后输入网络。具体参数为, 初始学习率1e-2, 批训练大小为8, 使用带有权重衰减的随机梯度下降发进行训练weightdecay=1e-4, 同时学习率的衰减采用poly策略, 具体为
| $\operatorname{lr}=\operatorname{init}_{\mathrm{lr}}{ }^*\left(1-\frac{\text { epoch }}{\text { num }_{\text {epoch }}}\right)^{\text {power }} ;$ | (6) |
本文进行的所有实验均在Pytorch深度学习框架下进行, CUDA版本为10.1, 系统为Ubuntu16.04, GPU为2张显存为11 GB的GeForceRTX 2080Ti。
为客观评价算法的有效性和优越性, 本文采用像素准确率(AP)、平均像素准确率(AMP)、平均交并比(MIoU)对结果进行评估。假定有k+1类(k个目标类和1个背景类)。具体地, pii表示真正例, 即实际为i类预测也为i类的像素个数, pij表示假负例, 即实际为i类却预测错为j类的像素个数, pji表示假正例, 即实际为j类却错误分为i类的像素个数。像素准确率AP为分类正确的像素点数和所有的像素点数的比值:
| $A_{\mathrm{p}}=\frac{\sum_{i=0}^k p_{i i}}{\sum_{i=0}^k \sum_{j=0}^k p_{i j}} ;$ | (7) |
考虑到数据集中每一类的样本量可能会非常不均匀, 引入平均像素准确率MPA。平均像素准确率为每一类分类正确的像素点数和该类的所有像素点数的比例然后求平均
| $A_{\mathrm{MP}}=\frac{1}{k+1} \sum\limits_{i=0}^k \frac{p_{i i}}{\sum\limits_{i=0}^k p_{i j}} ;$ | (8) |
平均交并比MIoU为计算每一类的IoU然后求平均:
| $\mathrm{MIoU}=\frac{1}{k+1} \sum\limits_{i=0}^k \frac{p_{i i}}{\sum\limits_{i=0}^k p_{i j}+\sum\limits_{i=0}^k p_{j i}-p_{i i}} .$ | (9) |
低秩重构模块的迭代次数T是一个超参数, 在不同迭代次数下模型表现如表 2所示。
|
|
表 2 不同迭代次数的模型表现 Table 2 Performance of models with different iterations |
在迭代次数T≥3后, 迭代次数的增加对模型基本没有影响, 因此模型默认值选择T=3, 与FCN、PSPNet、DeepLabV3进行实验结果的比较。
表 3的结果表明, LRR-Net像素准确率和平均交并比上优于其他算法, 但是在平均像素准确率上却低于PSPNet和DeepLabV3, 原因在于LRR-Net在占比较多的地物类别如林草地能实现更高的准确率, 但在占比较小的地物如裸地或工业区容易产生错误分类, 而PSPNet和DeepLabV3在不同地物表现更加平均。需要强调的是, LRR-Net在参数量更小的情况下实现了更高的精度。
|
|
表 3 高分三号数据集实验结果对比 Table 3 Comparison on GF-3 dataset |
为了更直观地对比算法对地物分类的效果, 图 6列出了各网络的分类结果图。从左到右依次为:SAR伪彩色图、真值标签、FCN、PSPNet、DeeplabV3、LRR-Net的分类结果。浅蓝色(0, 255, 255)代表水体, 黄色(255, 0, 0)代表建筑物, 绿色(0, 255, 0)代表林草地, 蓝色(0, 0, 255)代表工业区, 红色(255, 0, 0)代表土地裸地, 白色(255, 255, 255)代表其他。从图中可以看出, FCN因为参数量的不足, 导致网络表征能力不够, 出现了大量错分误分的情况。LRR-Net、PSPNet和DeepLabV3在整体表现差距不大, 但在细节上却有差异。分类结果中的黑色方框表明了各网络在细节上的不同。可以看出LRR-Net因为进行了低秩重构, 在分类边界上更加清晰, 表现更好, 相比PSPNet和DeeplabV3能够实现更连贯的分类, 从而提高了整体的分类精度。

|
Download:
|
| 图 6 分类结果图 Fig. 6 Images of classification results | |
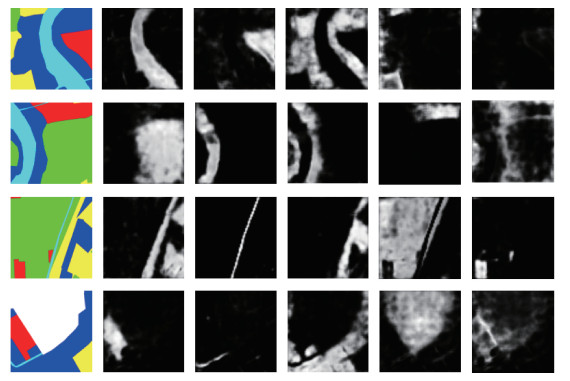
为了进一步证明低秩重构模块的合理性, 本文将隐变量Z即基分解后的图可视化。随机地选取几张测试集的图片输入, 并将它们经过网络的基分解后的隐变量图可视化。
由1.3可知, 隐变量Z的大小为N×K, 其中N=H×W, K为基的个数, 是一个超参数, 本文设置为64。可视化后的隐变量如图 7所示, 最左侧是标注好的地物标签, 右边5列则是经过低秩重构模块后基的可视化图中的5个。从图中可以看出, 可视化的基分解图已经可以收敛到具有特定语义类别的概念。这与本文在序言中所提到的基的特点一致, 即数量少且具有代表性, 能够独立地表示出一种具有高层语义的特征。因此, 经过这些基重构后的特征图也同样具有深层语义的特征, 避免了添加卷积层带来的冗余计算量。
|
Download:
|
| 图 7 基分解图可视化 Fig. 7 Visualization of base decomposition images | |
极化SAR地物分类一直是遥感领域研究的重点与难点。本文提出一个基于图像分割和EM算法的低秩重构网络模型LRR-Net。相比于现有的神经网络的图像分割模型, 本文的模型从传统的极化SAR基分解和低秩重构的角度出发, 以更少的参数量实现了更高的精度, 完成了传统极化SAR处理方法与神经网络的有机结合, 且不受数据限制, 可以用在各类有标签的图像分割问题处理上。针对卷积神经网络出现的高维信息冗余问题, 从极化目标分解的理念出发, 使用EM算法对高维空间的信息进行低秩重构, 从而解决了这一问题, 并在高分三号数据集上达到了接近88 % 的准确率。
虽然LRR-Net在参数量下降的前提下实现了更高的精度, 但仍有一些问题值得研究。例如, 在样本量较小的地物上LRR-Net的分类精度相对较低, 在分类的平衡性上表现不足。因此在后续的研究工作中, 将继续探索此类问题的解决方法。
| [1] |
Lee J S, Pottier E. 极化雷达成像基础与应用[M]. 洪文, 李洋, 尹嫱, 等译. 北京: 电子工业出版社, 2013.
|
| [2] |
赵昌锋. 基于深度学习的干涉SAR图像分类[D]. 西安: 西安电子科技大学, 2015.
|
| [3] |
张澄波. 综合孔径雷达: 原理、系统分析与应用[M]. 北京: 科学出版社, 1989.
|
| [4] |
Lee J S, Pottier E. Polarimetric radar imaging: from basics to applications[M]. Florida: CRC Press, 2009.
|
| [5] |
Ye X, Zhang H, Wang C, et al. Classification of high-resolution SAR imagery by Random Forest classifier[C]//2013 Asia-Pacific Conference on Synthetic Aperture Radar(APSAR). September 23-27, 2013, Tsukeba, Japan. IEEE, 2013: 312-316.
|
| [6] |
Demirhan M E, Salor Ö. Classification of targets in SAR images using SVM and k-NN techniques[C]//2016 24th Signal Processing and Communication Application Conference(SIU). May 16-19, 2016, Zonguldak, Turkey. IEEE, 2016: 1581-1584. DOI: 10.1109/SIU.2016.7496056.
|
| [7] |
Hou B, Yang C, Ren B, et al. Decomposition-feature-iterative-clustering-based superpixel segmentation for PolSAR image classification[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(8): 1239-1243. Doi:10.1109/LGRS.2018.2833492 |
| [8] |
Deng L. Deep learning: methods and applications[J]. Foundations and Trends in Signal Processing, 2014, 7(3/4): 197-387. Doi:10.1561/2000060039 |
| [9] |
Chen Y Q, Jiao L C, Li Y Y, et al. Multilayer projective dictionary pair learning and sparse autoencoder for PolSAR image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(12): 6683-6694. Doi:10.1109/TGRS.2017.2727067 |
| [10] |
Liu H Y, Yang S Y, Gou S P, et al. Polarimetric SAR feature extraction with neighborhood preservation-based deep learning[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(4): 1456-1466. Doi:10.1109/JSTARS.2016.2618891 |
| [11] |
Zhu H L, Lin N, Leung H, et al. Target classification from SAR imagery based on the pixel grayscale decline by graph convolutional neural network[J]. IEEE Sensors Letters, 2020, 4(6): 1-4. Doi:10.1109/LSENS.2020.2995060 |
| [12] |
Zhang Z M, Wang H P, Xu F, et al. Complex-valued convolutional neural network and its application in polarimetric SAR image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(12): 7177-7188. Doi:10.1109/TGRS.2017.2743222 |
| [13] |
Dempster A P, Laird N M, Rubin D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1977, 39(1): 1-22. Doi:10.1111/j.2517-6161.1997.tb01600.x |
| [14] |
Li X, Zhong Z S, Wu J L, et al. Expectation-maximization attention networks for semantic segmentation[C]//2019 IEEE/CVF International Conference on Computer Vision(ICCV). October 27-November 2, 2019, Seoul, Korea(South). IEEE, 2019: 9166-9175. DOI: 10.1109/ICCV.2019.00926.
|
| [15] |
He K M, Zhang X Y, Ren S Q, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. June 27-30, 2016, Las Vegas, NV, USA. IEEE, 2016: 770-778. DOI: 10.1109/CVPR.2016.90.
|
| [16] |
Hu J, Shen L, Albanie S. Squeeze-and-excitation networks[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. June 18-23, 2018, Salt Lake City, UT, USA. IEEE, 2018: 7132-7141. DOI: 10.1109/CVPR.2018.00745.
|
| [17] |
刘杰, 张庆君. 高分三号卫星及应用概况[J]. 卫星应用, 2018(6): 12-16. Doi:10.3969/j.issn.1674-9030.2018.06.006 |
| [18] |
Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition. June 7-12, 2015, Boston, MA, USA. IEEE, 2015: 3431-3440. DOI: 10.1109/CVPR.2015.7298965.
|
| [19] |
Zhao H S, Shi J P, Qi X J, et al. Pyramid scene parsing network[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. July 21-26, 2017, Honolulu, HI, USA. IEEE, 2017: 6230-6239. DOI: 10.1109/CVPR.2017.660.
|
| [20] |
Chen L C, Papandreou G, Kokkinos I, et al. Deeplab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(4): 834-848. Doi:10.1109/TPAMI.2017.2699184 |
 2022, Vol. 39
2022, Vol. 39 


