2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
近年来,无线通信系统得到快速的发展和更新,新技术的兴起、通信用户数量的激增,导致频谱需求的爆发性增长和频谱资源的极度短缺。大量测量和研究结果表明,频谱资源短缺与频谱资源处于空闲状态的情况是同时存在的[1-2]。
认知无线电(cognitive radio, CR)技术是一种可以与工作环境进行信息交换并可改变自身参数的无线电系统,其允许认知用户对授权用户的授权无线频谱进行感知,若检测到频谱空闲时就能短暂使用该段资源。而频谱感知是实现该系统功能的重要环节和关键所在[3-5]。
频谱感知是主动式获取频谱资源使用情况的方法,常见的发射端检测可概括为:匹配滤波器检测、循环平稳特征检测和能量检测等[6]。
匹配滤波器检测可在极短时间内获得高处理增益,但缺点是需要授权用户信号的先验知识,同时需要授权用户信号与认知用户的精确同步信息[7]。循环平稳特征检测具有很强的抗干扰能力,也可区分信号类型,缺点是需要授权用户信号的循环频率,同时需要较长观测时间和高的计算复杂度[8]。能量检测是最基础和广泛应用的,根据一段检测空间(时域或频域)内接收到的信号的总能量来判断是否存在有效的通信信号。其计算复杂度小且不需要授权用户的先验知识,缺点是对噪声的不确定性敏感且不能准确区分信号类型[9]。
此外,部分频谱感知的研究也应用了近年来兴起的技术,如机器学习、神经网络等,文献[10]利用神经网络较强的多分类能力实现合作频谱感知,但在低噪声环境下性能较差;文献[11]对隐马尔科夫模型框架下的能量检测算法进行无监督学习,但对频谱状态的驻留时间分布存在要求。
目前发展和应用的较为成熟的频谱感知技术主要针对的是窄带频谱的场景,但为了快速发现并利用更多的频谱资源和提高检测效率,就需要实现宽频带的频谱感知。
一类是以标准模数采样转换器,直接获取宽带信号或以滤波器组的混频技术,将其划分为若干窄带频谱并进行检测,但前者对硬件水平要求较高、后者因需要大量射频器件而成本较高。如文献[12]基于模拟滤波器的搜索方法以提高扫描速度和减少测量数量,但其考虑的子频带带宽是相等的;文献[13]是以滤波器组为基础的考虑空间分布的协作检测,但其需要预知噪声带的位置及其功率;文献[14]基于小波变换对子频带分组,检测上升沿和下降沿,但因算法复杂度高而难以实现。
另一类是以压缩感知[15]为理论基础的宽带频谱感知技术,在信号具有稀疏性的前提下,以采样率小于2倍带宽仍可恢复原始信号。如文献[16]以欠采样后得到的数据恢复循环自相关函数来确定频谱感知结果,但其具有较高的复杂度和较大的时延;文献[17]以矩阵填充和稀疏信号的重构进行基于压缩感知的宽带协作感知,但感知时间过长。
针对上述研究的不足,本文的宽频带频谱感知中的快速边界识别方法,通过检测窗比值实现子频带边界的识别,通过能量检测对各个子频带的占用状态进行判定。该方法无需预知噪声带位置与功率,也不需要授权用户的先验知识;适用于子频带带宽不一致、且其数量未知的场景;算法复杂度低、感知帧数少、易于应用和硬件实现;采用子频带合并与修正阈值方法来减少误判。仿真结果表明,方法不仅适用于宽带频谱盲感知,且在低信噪比情况下具有较好的性能。
1 基于比值的能量检测算法边界识别 1.1 系统模型能量检测法的频谱感知流程如图 1所示。

|
Download:
|
| 图 1 能量检测的频谱感知流程 Fig. 1 Spectrum sensing process of energy detection | |
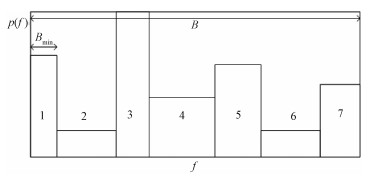
对于宽频带的场景,在预知子频带的带宽和数目的情况下,可以使用多信道宽带频谱感知方式,将宽带频谱均分为若干窄带频谱,先使用串行扫描或并行扫描两种方式,再使用相应的感知算法进行检测。两种方式虽然不需要高速ADC,但是串行扫描会带来较大的感知时延、而并行扫描则需要大量的射频模块[18]。且在信号带与噪声带的宽度不一致、子频带带宽和数目均未知的情况下就不再适用,图 2表示这样一种宽频带信号的功率谱密度图。其中,2号与6号子频带为空白子频带(仅含有噪声信号),其余子频带均被占用但其功率谱密度不同。
|
Download:
|
| 图 2 宽频带信号的功率谱密度 Fig. 2 The PSD of a wide-band signal | |
通常来说,频谱感知是认知用户(secondary user, SU)在某频域区间内对授权用户(primary user, PU)的存在与否进行判断的二元假设模型
| $ \begin{array}{c} H_0: r(t)=w(t), \\ H_1: r(t)=h(t) \times s(t)+w(t), 0 \leqslant t \leqslant T_t . \end{array} $ | (1) |
其中: r(t)表示认知用户的接收信号;s(t)表示授权用户的发射信号;w(t)表示噪声信号;h(t)表示无线信道的增益;Tt为总的感知时间。为简单起见,假设SU与PU之间的信道为加性高斯白噪声信道,此时h(t)可视为1[19]。H0表示在t时刻PU信号不存在的情况,而H1表示PU信号存在的情况。则采样后的二元假设模型为
| $ \begin{array}{c} H_0: r[n]=w[n], \\ H_1: r[n]=s[n]+w[n], n=1, 2, 3, \cdots, N_s . \end{array} $ | (2) |
其中: Ns是在感知时间Ts内的采集样本总数; 同样地,H0和H1的表示与式(1)中相同。假设噪声信号w[n],对于所有的n,均是独立恒等分布(i.i.d)且具有未知方差σw2的零均值循环对称复形高斯随机函数,则r[n]的离散傅里叶变换由文献[20]中给出为
| $ \begin{array}{c} r[k] = \sum_{n = 1}^{{N_s}} {\frac{{r[n]{{\exp }^{\frac{{ - {\rm{i}}2{\rm{ \mathsf{ π} }}(k - 1)(n - 1)}}{{{N_s}}}}}}}{{\sqrt {{N_s}} }}} , \\ k = 1, 2, 3, \cdots , {N_s}. \end{array} $ | (3) |
定义
| $ p(f) \triangleq|r[k]|^2, (k-1) \Delta f \leqslant f \leqslant k \Delta f, \forall k. $ | (4) |
边界检测的相关方法中,传统的有能量阈值法、一阶导数法等因易受到噪声影响而性能较差,小波变换法虽有更好的性能但实现困难。本文借鉴文献[21]提出的通用能量检测中的边界检测方法,即基于检测窗比值的方法,针对CR网络的最大吞吐量对感知时间进行优化以期得到更好的性能。
考虑一个频域区间为BHz上工作的宽带CR网络,同样以图 2为例,不同的子频带具有不同的功率谱密度。子频带依H0和H1假设分为未被PU占用和被PU占用的不同情况,SU仅可利用空白子带(只有噪声信号)进行通信。
该网络的频谱感知帧结构如图 3所示。

|
Download:
|
| 图 3 认知无线电网络的感知帧结构 Fig. 3 The sensing frame structure of a CR network | |
图 3表示了L个连续的感知帧(以下简称为帧),每个帧的持续时间为Tf,其中用于频谱感知的时间为Ts,为了得到目标帧(第i帧)中各个子频带的边界位置与占用状态,需要对其之前的L-1帧进行检测,从而实现对子频带的边界识别。
为了更好地解释和说明,所提出的边界识别方法在以下假设均成立的情况下适用:1)在每一帧中,各个子频带的噪声方差没有变化,但在帧之间可以变化;2)对于连续的L个帧,各个子频带的边界保持不变,但是帧与帧之间子频带的PSD可能发生变化;3)被检测的频带至少包含一个空白子带,但其位置是未知的;4)每个子频带的带宽至少为Bmin,且子频带的个数至少为2,但子频带的总数Sb是未知的。
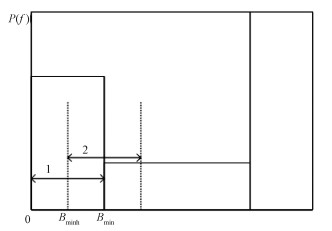
通常而言,子频带的边界识别可以由该子频带与相邻子频带的PSD差值来表征,如图 2所示。设置一个频域区间大小为Bmin的检测窗,比较该检测窗左、右各Bminh宽内的平均能量,就可确定子带的边界,如图 4所示,以矩形窗为例进行分析,但在实际情况中,信号带子频带的边界和成型窗没有这样理想化,会使得检测结果出现误差。
|
Download:
|
| 图 4 检测窗示例 Fig. 4 A simple of the detection window | |
为了方便分析,将检测窗起点分别设置为0和Bminh处,考虑检测窗标记1和2的左、右半窗能量比值关系:
| $ \;\;\;V_{\mathrm{edge}}=\frac{A_{\mathrm{e}}\left[0: B_{\text {minh }}\right]}{A_{\mathrm{e}}\left[B_{\operatorname{minh}}: B_{\min }\right]} \approx 1, \\ V_{\mathrm{edge}}=\frac{A_{\mathrm{e}}\left[B_{\operatorname{minh}}: B_{\min }\right]}{A_{\mathrm{e}}\left[B_{\min }: B_{\min }+B_{\operatorname{minh}}\right]} \neq 1 . $ | (5) |
其中:符号Ae[x, y]表示频域区间[x, y]内的平均能量,Bminh=Bmin/2。可以发现当检测窗内不存在边界时,左右各半检测窗的平均能量比值约等于1。那么,判断并识别子频带边界的过程就可转化为检测Vedge的比值关系。同时,可以发现当检测窗的中间点恰好处于子频带边界处时,该比值恰好为范围内的极值,即该极值处就为边界的位置。在不失一般性的情况下,将该检测窗的起点由频域区间[0, B-Bmin]依次滑动,就可以用上述方法检测并识别出所有子频带的边界。最后,对于所有的边界结果,依次挑选比值关系最大的边界处,并将其左右各Bmin/2区间内的边界结果去除,以减少误判。
将式(4)与式(5)整合,可以得到[0, Bminh]及[Bminh, Bmin]上功率谱密度函数p(f)即平均能量为
| $ \begin{array}{c} A_{\mathrm{e}}\left[0: B_{\text {minh }}\right]=\sum_{k=1}^{N_{\mathrm{eh}}} \frac{|r[k]|^2}{N_{\mathrm{eh}}} \triangleq E_a, \\ A_{\mathrm{e}}\left[B_{\text {minh }}: B_{\min }\right]=\sum_{k=1}^{N_{\mathrm{eh}}} \frac{\left|r\left[k+N_{\mathrm{eh}}\right]\right|^2}{N_{\mathrm{eh}}} \triangleq E_b . \end{array} $ | (6) |
其中:Neh是在频域大小Bminh的区间内的采样点数,对于实际的认知无线电网络而言,Neh是一个较大的数,因此可以将中心极限定理(CLT)应用于式(6),为了方便起见,定义
| $ R_{\text {edge }}=\frac{E_a}{E_b}. $ | (7) |
对于式(7)的这样一个实值函数
| $ \sqrt{N_{\mathrm{eh}}}\left(R_{\text {edge }}-\overline{R_{\text {edge }}}\right) \sim N\left(0, \sigma_e^2\right). $ | (8) |
其中:
| $ \sqrt{N_{\text {eh }}}\left(\left[E_a, \overline{E_a}\right]^{\mathrm{T}}-\left[E_b, \overline{E_b}\right]^{\mathrm{T}}\right) \sim N(0, \boldsymbol{\varphi}). $ | (9) |
| $ \boldsymbol{a}=\left[\frac{\partial R_{\text {edge }}}{\partial E_a}, \frac{\partial R_{\text {edge }}}{\partial E_b}\right]_{E_a=\overline{E_a}, E_b=\overline{E_b}}^{\mathrm{T}}=\left[\frac{1}{\overline{E_b}}, -\frac{\overline{E_a}}{\overline{E_b^2}}\right]^{\mathrm{T}} . $ | (10) |
其中:式(9)的证明可参见文献[22]中122页3.3.A小节。首先考虑边界不存在的情况时,可记做假设He0,在该情况下,可得
| $ \begin{array}{c} \sigma_e^2= \boldsymbol{a}^{\mathrm{T}} \boldsymbol{\varphi} \boldsymbol{a}=\left[\frac{1}{\overline{E_b}}, -\frac{\overline{E_a}}{\overline{E_b^2}}\right] \boldsymbol{\varphi}\left[\frac{1}{\overline{E_b}}, -\frac{\overline{E_a}}{\overline{E_b^2}}\right]^{\mathrm{T}} \\ =\left[\frac{1}{e_0}, -\frac{1}{e_0}\right] \boldsymbol{\varphi}\left[\frac{1}{e_0}, -\frac{1}{e_0}\right]^{\mathrm{T}}. \end{array} $ | (11) |
其中,
| $ \begin{array}{c} \boldsymbol{\varphi}=\left[\begin{array}{cc} N_{\mathrm{eh}}\left(E\left\{E_a E_a^{\mathrm{H}}\right\}-\overline{E_a^2}\right) & 0 \\ 0 & N_{\mathrm{eh}}\left(E\left\{E_b E_b^{\mathrm{H}}\right\}-\overline{E_b^2}\right) \end{array}\right] \\ =\left[\begin{array}{cc} E_{a 4}-\overline{E_a^2} & 0 \\ 0 & E_{b 4}-\overline{E_b^2} \end{array}\right] . \\ \end{array} $ | (12) |
可得,
| $ \sigma_e^2=\frac{E_{a 4}+E_{b 4}-2 e_0^2}{e_0^2}. $ | (13) |
其中: Ea4、Eb4分别为Ea、Eb的四阶矩,在He0情况下,Ea4=Eb4=2e02。则式(11)的最终结果为σe2=2。在L-1个连续的帧内,子频带的边界保持不变,考虑边界检测窗的检测统计量YL:
| $ Y_L=\frac{1}{L-1} \sum_{i=1}^{L-1} Y_{e i}. $ | (14) |
| $ Y_e=\sqrt{\frac{N_{\mathrm{eh}}}{2}}\left(\frac{E_a}{E_b}-1\right). $ | (15) |
其中Yei为式(13)中Ye在第i个帧中的对应值。在He0情况,即在边界不存在的假设下,由式(9)至式(15)可知,Ye~N(0, 1),因此YL~N(0, 1/(L-1))。设定该统计量的比较阈值为λe,则可以计算虚警概率为
| $ P_{e f}=P\left(Y_L>\lambda_e \mid H_{e 0}\right)=Q\left(\sqrt{L-1} \lambda_e\right). $ | (16) |
其中Q(.)为标准正态分布的右尾函数。同理,在边界存在的假设下,即He1情况下,参照He0时的相关推导过程,可得Ye~N(μe, σHe12)及μe=
| $ \begin{array}{c} P_{e d}=P\left(Y_L>\lambda_e \mid H_{e 1}\right) \\ =Q\left[\sqrt{L-1}\left(\frac{\lambda_e-\sqrt{N_{\mathrm{eh}}} \rho_e}{1+\rho_e}\right)\right]. \end{array} $ | (17) |
由上述推理分析过程可见,基于检测窗比值的边界识别方法是可行的,可根据恒定虚警规则设置相应的阈值,而最终的检测性能还和感知帧数、信噪比等因素有关。
1.3 子频带状态判定上述过程对子频带的边界进行了检测识别,但并不能由此判断子频带的占用状态,即不能简单以由下降沿到上升沿的频域区间作为噪声带,如图 2中的4号子频带。因此,需要后续过程对各个子频带的占用状态进行判定。
使用上一节的方法,在已确定每个子频带边界的情况下,可以式(4)为基础,计算出各个子频带的平均能量,并从中选择一个参考的子频带,一般选择噪声带,且该选择可以有多种标准:如取若干子频带能量的平均值、平均第二小的子频带的能量等。为简单分析,选择平均能量最小的子频带作为参考的子频带,并以其平均能量作为参考能量。
假设在宽频带中的检测出的子频带总数目为n,将其中的子频带分别标记为:B1, B2, ⋯, Bn。由前文假设,2≤n≤nmax,其中nmax=
| $ \begin{array}{l} E\left(B_i\right)=\frac{1}{N_i} \sum_1^{N_i}\left|r\left[k+N_{s i}\right]\right|^2 \triangleq E_i, \\ E\left(B_j\right)=\frac{1}{N_j} \sum_1^{N_j}\left|r\left[k+N_{s j}\right]\right|^2 \triangleq E_j. \end{array} $ | (18) |
其中: E(Bi)、E(Bj)分别表示第i、j个子频带的平均能量,Ni、Nj分别为2个子频带内的采样点数,Nsi、Nsj分别为2个子频带采样前的采样点数。类似式(15),可定义如下检测统计
| $ R_j=\sqrt{\frac{N_j N_i}{N_i+N_j}}\left(\frac{E_j}{E_i}-1\right) . $ | (19) |
在第j个子频带为噪声带的假设情况下,记做Hj0,可得Rj~N(0, 1),而在第j个子频带为信号带的假设情况下,记做Hj1下,可得Rj~
| $ \lambda_j^*=\lambda_j\left(1-a\left(\rho_j-\rho_\lambda\right)\right), \rho_j \leqslant \rho_\lambda . $ | (20) |
其中ρλ为设定的修正信噪比的阈值,当实际信噪比低于该值时对阈值进行修正,a为修正系数,由此可计算在阈值为λj*时,该统计量的检测概率和虚警概率为
| $ \begin{array}{c} P_{i f}=P\left(R_j>\lambda_j^* \mid H_{j 0}\right)=Q\left(\lambda_j^*\right), \\ P_{j d}=P\left(R_j>\lambda_j^* \mid H_{j 1}\right)=Q\left(\frac{\lambda_j^*-\sqrt{\frac{N_j N_i}{N_i+N_j}} \rho_j}{1+\rho_j}\right). \end{array} $ | (21) |
由以上推导和分析可见,使用上述方法可以对宽频带中的各个子频带的边界进行检测识别并对子频带的占用状态进行判定。此外,为避免因边界检测结果带来的误差,可对相同占用状态且平均能量接近的子频带进行合并,之后得到最终的检测结果。
2 仿真结果及分析整个实验仿真是在Matlab下进行的,所使用的软件版本为9.4.0 (R2018a)。在实验中,仿真是以总带宽B为400 MHz并以奈奎斯特采样率采样后得到的信号为对象的,信道均为加性高斯白噪声信道。此外, 分别设定边界检测的虚警概率Pef=0.01、以及子频带占用的虚警概率Pjf=0.1、FFT点数设定为2 048、信噪比步长设置为1 dB。在后续若无其他表述,说明仿真是以上述默认设定值加以约束的。
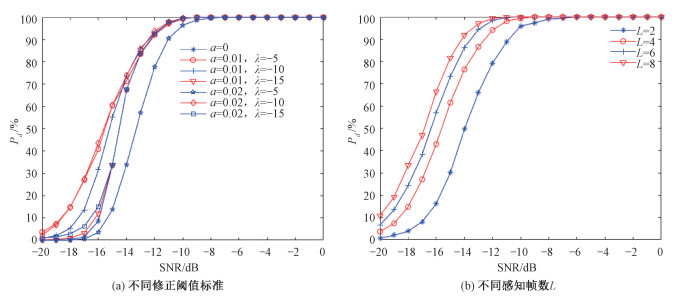
图 5(a)是在不同修正阈值下的检测概率随信噪比的变化曲线,所用信号为频域占用率约10%的OFDM(orthogonal frequency-division multiplexing, 正交频分复用)宽带信号,每组实验均是10 000次仿真运行后的结果。其中,除默认设定的虚警概率、FFT点数、信噪比步长外,感知帧数设定为4,图中a为修正系数、λ对应式(18)中ρλ即修正信噪比阈值。在a=0时,即不进行阈值修正时,在低信噪比情况下会出现检测概率骤降的情况,这是因为,较低的感知帧数以及子频带边界的识别过程导致用于估计噪声功率的带宽并不能满足远远大于信号带带宽的条件,在估计时造成估计值偏高的情况。对于图中不同a、λ取值下的检测概率,从结果可发现,选取两者合适的值对阈值进行修正能有效提高在低信噪比情况下的检测概率,如在信噪比为-15 dB处,a取值为0,即未修正前检测概率结果为33.79%,而以a取值为0.01,λ取值为-5 dB对原阈值修正后检测概率可达60.48%。
|
Download:
|
| 图 5 快速边界识别方法的性能 Fig. 5 The performance of fast edge detection method | |
图 5(b)是不同的感知帧数下检测概率随信噪比的变化曲线,所用信号为频域占用率约10%的OFDM宽带信号,每组实验均是10 000次仿真运行后的结果。其中,除默认设定的虚警概率、FFT点数、信噪比步长外,设定修正信噪比阈值ρλ=-5 dB,修正阈值系数a=0.01。可以发现,随着信噪比的提高,检测概率逐渐变高这一整体趋势是相同的,而随着感知帧数L值的增加,检测概率相应变高,这是因为,更多的感知帧数使得边界检测的结果和噪声功率的估计结果变得更加准确。这一点在低信噪比情况下较为明显,如在信噪比为-15 dB处,L取值为2、4、6、8的检测概率结果分别为30.06%、61.48%、73.20%和81.65%,由此可见,选择合适的感知帧数进行检测能有效提高低信噪比时的检测概率。此外,方法在低信噪比情况下也展示出了较好的检测性能,如在L取值为8时,当信噪比达到-14 dB及以上时检测概率有90%以上。
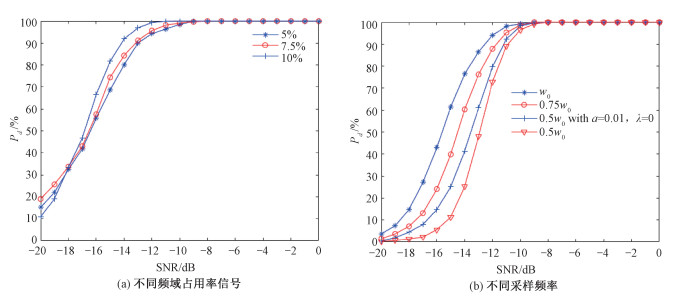
图 6(a)是对于不同频域占用率的宽带信号的检测概率随信噪比的变化曲线,因为在实际环境中,频谱占用率基本在5% ~15%,因此选择频域占用率为5%、7.5%、10%的OFDM信号进行仿真实验,每组实验均是10 000次仿真运行后的结果。其中,除默认设定的虚警概率、FFT点数、信噪比步长外,感知帧数L值设定为8,设定修正信噪比阈值ρλ=-5 dB,修正阈值系数a=0.01。从结果可以发现,随着信噪比提高,检测概率逐渐变高,具体而言,检测概率的结果间的差距会受到子频带的数目、功率谱密度图形状等因素影响,但检测概率随信噪比增加而提高的总体趋势是相同的,也证实了本文方法对于具有不同频域占用率的信号的适用性,如在信噪比为-18 dB处,三者的检测概率结果分别为32.48%、33.80%和33.36%。
|
Download:
|
| 图 6 快速边界识别方法对宽频带信号的适用性 Fig. 6 Applicability of fast edge detection method with wide-band signal | |
图 6(b)是在不同采样频率下检测概率随信噪比的变化曲线,选择了频谱占用率为10%的宽带OFDM信号,每组实验均是10 000次仿真运行后的结果。其中,除默认设定的虚警概率、FFT点数、信噪比步长外,感知帧数L值设定为4,由上至下的4条曲线,分别对应以w0、0.75w0、0.5w0和0.5w0采样率下的检测结果。其中,w0为奈奎斯特采样率,第1、2、4条曲线的修正阈值表达为ρλ=-5 dB,a=0.01,而第3条曲线的修正阈值表达为ρλ=0 dB,a=0.01。从结果看,降低采样频率会减少检测概率,尤其是在低信噪比情况下较为明显。此外,调整修正阈值能够提高欠采样情况下的检测概率。如在-14 dB处、检测概率分别为76.43%、60.31%、41.37%和25.25%。可见,本文方法在降低采样频率的实际应用是硬件条件有限的情况下,能以此检测更宽带宽的信号,可弥补硬件条件不足带来的影响,但这样做的前提是被占用的相邻子频带间的距离要足够大、尽管可以通过调整修正阈值提高检测概率,但在低信噪比情况下的检测概率仍较低。
3 总结常见的频谱感知方法中,以能量检测、匹配滤波器检测和循环平稳检测为例,在以此进行宽频带频谱感知时,采用多信道宽带频谱感知的形式进行协同感知,而无论串行扫描或是并行扫描的方式都有明显不足。同时,相关方法也会因自身基本原理影响带来一定的局限性。此外,在处理信号带与噪声带的子频带宽度不一致、子频带的带宽和数目均未知的情况时就不再适用,需要做进一步的处理而带来较大的处理时延。相关方法与本文方法在宽频带频谱感知场景下的比较详见表 1。
|
|
表 1 不同频谱感知方法对宽频带信号的适用性 Table 1 The applicability of different spectrum sensing methods for wide-band signals |
高效准确的实现宽带频谱感知对于提高频谱利用率有着重大意义,传统方法各有不足且不适用于宽频带场景,过渡方法局限性较大且适用场景少,压缩感知性能虽好但复杂度高且时延较大。本文的宽频带频谱感知中的快速边界识别方法,以检测窗比值实现子频带边界的识别,以能量检测对各个子频带的占用状态加以判定。在兼具能量检测实现简单、易于硬件实现的优势同时,以多感知帧和阈值修正的方法降低因噪声估计误差带来的不利影响。
仿真表明,本文方法适用于不同频域占用率的宽带信号,且在低噪声情况下具有较好的性能;适当增加感知帧数可提高检测率,而该值一般较小(L < 10)即可,所需样本数和感知时延较小;无需处理因不一致情况而带来的额外判定过程,适用于各子频带带宽数目均未知的场景;所需先验知识少,无需预知授权用户的先验知识,也无需预知噪声功率;在信号子频带间间距足够大的情况下,可适当减小采样频率以在硬件条件有限的情况下检测更大的带宽。可见,本文方法的适用性更广且在宽频带信号频谱感知情况下更快速。
| [1] |
徐大钧. 5G移动通信中的动态频谱共享简述[J]. 中国无线电, 2017(8): 26-28. |
| [2] |
Kulkarni P, Chin W H, Farnham T. Radio resource management considerations for LTE Femto cells[J]. ACM SIGCOMM Computer Communication Review, 2010, 40(1): 26-30. Doi:10.1145/1672308.1672314 |
| [3] |
FCC. Facilitating opportunities for flexible, efficient and reliable spectrum use employing cognitive radio technologies[R]. The FCC adopt role changes for Smart Radios, 2005.
|
| [4] |
Tandra R, Mishra S M, Sahai A. What is a spectrum hole and what does it take to recognize one?[J]. Proceedings of the IEEE, 2009, 97(5): 824-848. Doi:10.1109/JPROC.2009.2015710 |
| [5] |
周小飞, 张宏纲. 认知无线电原理及应用[M]. 北京: 北京邮电大学出版社, 2007: 8-36.
|
| [6] |
Akyildiz I F, Lee W Y, Vuran M C, et al. NeXt generation/dynamic spectrum access/cognitive radio wireless networks: a survey[J]. Computer Networks, 2006, 50(13): 2127-2159. Doi:10.1016/j.comnet.2006.05.001 |
| [7] |
Cabric D, Mishra S M, Brodersen R W. Implementation issues in spectrum sensing for cognitive radios[C]// Conference Record of the 38th Asilomar Conference on Signals, Systems and Computers, 2004. November 7-10, 2004, Pacific Grove, CA, USA. IEEE, 2004: 772-776.
|
| [8] |
Gardner W A. Exploitation of spectral redundancy in cyclostationary signals[J]. IEEE Signal Processing Magazine, 1991, 8(2): 14-36. Doi:10.1109/79.81007 |
| [9] |
Liu X, Chen K Q, Yan J H, et al. Optimal energy harvesting-based weighed cooperative spectrum sensing in cognitive radio network[J]. Mobile Networks and Applications, 2016, 21(6): 908-919. Doi:10.1007/S11036-016-0711-y |
| [10] |
薛建伟, 唐亮, 卜智勇. 基于神经网络的认知无线电合作频谱感知[J]. 中国科学院大学学报, 2020, 37(3): 379-386. Doi:10.7523/j.issn.2095-6134.2020.03.011 |
| [11] |
狄路杰. 基于机器学习的认知无线电频谱感知技术研究[D]. 成都: 电子科技大学, 2019.
|
| [12] |
Yoon S, Li L E, Liew S C, et al. QuickSense: fast and energy-efficient channel sensing for dynamic spectrum access networks[C]//2013 Proceedings IEEE INFOCOM. April 14-19, 2013, Turin, Italy. IEEE, 2013: 2247-2255. DOI:10.1109/INFCOM.2013.6567028.
|
| [13] |
Quan Z, Cui S G, Sayed A H, et al. Optimal multiband joint detection for spectrum sensing in cognitive radio networks[J]. IEEE Transactions on Signal Processing, 2009, 57(3): 1128-1140. Doi:10.1109/TSP.2008.2008540 |
| [14] |
Taherpour A, Gazor S, Nasiri-Kenari M. Wideband spectrum sensing in unknown white Gaussian noise[J]. IET Communications, 2008, 2(6): 763-771. Doi:10.1049/IET-COM%3A20070410 |
| [15] |
Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. Doi:10.1109/TIT.2006.871582 |
| [16] |
Xuan S, Zhou Z, Li B. CS-feature detection spectrum sensing algorithm for cognitive radio[J]. International Journal on Advances in Information Sciences and Service Sciences, 2012, 4(1): 37-45. Doi:10.4156/aiss.vol4.issue1.5 |
| [17] |
Prema G, Narmatha D. Performance of energy aware cooperative spectrum sensing algorithms in cognitive wireless sensor network[C]//2016 Online International Conference on Green Engineering and Technologies (IC-GET). November 19, 2016, Coimbatore, India. IEEE, 2016: 1-6. DOI:10.1109/GET.2016.7916791.
|
| [18] |
任诗雨. 基于多路采样的宽带频谱感知技术研究[D]. 北京: 北京邮电大学, 2017.
|
| [19] |
Kumar B N, Prema S C. Noise variance estimation through penalized least-squares for ED-spectrum sensing[C]//2016 International Conference on Communication Systems and Networks (ComNet). July 21-23, 2016, Thiruvanan-thapuram, India. IEEE, 2016: 23-27.
|
| [20] |
Stoica P, Moses R L. Spectral analysis of signals[M]. Upper Saddle River, NJ, USA: PRENTICE HALL, 2005.
|
| [21] |
Bogale T E, Vandendorpe L, Le L B. Wide-band sensing and optimization for cognitive radio networks with noise variance uncertainty[J]. IEEE Transactions on Communications, 2015, 63(4): 1091-1105. Doi:10.1109/TCOMM.2015.2394390 |
| [22] |
Serfling R J. Approximation theorems of mathematical statistics[M]. Hoboken, NJ, USA: John Wiley & Sons, Inc., 1980.
|
| [23] |
Bogale T E, Vandendorpe L. Moment based spectrum sensing algorithm for cognitive radio networks with noise variance uncertainty[C]//2013 47th Annual Conference on Information Sciences and Systems (CISS). March 20-22, 2013, Baltimore, MD, USA. IEEE, 2013: 1-5.
|
 2022, Vol. 39
2022, Vol. 39 


