面对第5代(fifth generation, 5G)移动通信场景中智能终端和多媒体应用的爆发式增长,传统蜂窝网络已无法支持海量的设备接入和10 Gbit/s以上的高速数据传输[1]。D2D通信是LTE-A为卸载蜂窝基站流量而提出的设备间直接通信模式,它允许短距离通信设备复用蜂窝频谱直接建立本地连接,以此对蜂窝通信进行补充,实现超高数量的终端连接、更高的频谱效率和更大的系统吞吐量[2-4]。D2D终端各种形式的能量采集为D2D设备的绿色通信和灵活部署提供了有效方案。其中射频能量采集D2D通信受到广泛关注,它利用空间内丰富的射频信号为D2D设备充电,实现了D2D通信的可持续性[5]。
文献[6-7]研究传统射频能量采集D2D通信,考虑采集射频信号中的能量解决D2D发射端能量受限问题。文献[6]提出一种新的认知D2D通信模型,该模型中D2D发射端对干扰射频能量进行采集并完成数据传输,作者利用随机几何理论分析了两种蜂窝信道接入策略对能量采集D2D通信中断概率的影响。文献[7]提出能量站(power beacons, PBs)概念,D2D发射端先收集已部署PBs的射频能量,再复用蜂窝频谱资源进行数据传输,分析了不同能量传输模型下的射频能量采集中断概率和D2D保密中断概率。除了面向D2D发射端,射频能量采集技术同样可对能量受限的D2D接收端充电,以满足其后续的数据传输需求或信号处理需求。
文献[8-9]研究无线信息与能量同步传输(simultaneous wireless information and power transfer, SWIPT)的基本原理,该技术允许射频信号同时传输能量和信息。SWIPT主要包含功率切片和时间转换两种模式:功率切片模式允许射频接收机将射频信号切分为两部分,一部分用于信息解码,另一部分用于能量采集;时间转换模式允许射频接收机在时间上先进行射频能量采集,再进行信息解码。尽管射频能量采集的能量转化效率不高,但D2D设备的发射功率需求一般较低,这使SWIPT-D2D的研究具有一定意义。因此,将SWIPT应用到D2D通信是一种解决D2D接收端能量受限并维持高速数据传输的有效解决方案。
文献[10-12]对SWIPT-D2D通信的功率控制和功率切片控制(或时间转换控制)问题进行了探索。文献[10]研究支持SWIPT的蜂窝系统中具有部分信道状态信息的D2D通信功率控制问题,其中蜂窝用户具有功率切片能力,在保证蜂窝用户能量采集需求和速率需求条件下,最大化D2D通信速率。文献[11]考虑蜂窝用户与D2D用户采用时间转换模式的SWIPT进行射频能量采集和信息解码,并为解决功率控制和时间转换控制联合优化问题提出两种策略。文献[12]假设配备功率切片设备的D2D用户提前确定好复用的蜂窝频谱,据此建立全新的博弈模型,每个D2D链路同时选择发射功率和功率切片因子,以使其效用最大化。
除上述资源分配问题,如何通过信道分配和模式选择提升SWIPT-D2D系统的能效也被广泛研究。文献[13]利用随机几何理论对系统进行建模,考虑D2D用户具备射频能量采集能力(功率切片和时间转换两种模式),分析D2D用户复用蜂窝频谱模式,D2D专用频谱模式以及蜂窝模式下的能效,为提升D2D通信能效提供了先进的模式选择机制,同时证明了SWIPT可以增大D2D通信的能效。文献[14]考虑D2D用户复用蜂窝下行链路频谱,所有用户均配备功率切片设备,基于匹配理论完成了用户的信道分配和功率控制,仿真表明所提算法显著提升了D2D用户能效和蜂窝用户的射频能量采集量。
大量文献研究了SWIPT-D2D通信系统中的资源分配问题[10-14],但尚无文献考虑对频谱匹配、功率控制和功率切片控制的联合优化。另外,现有文献均考虑D2D设备复用单个蜂窝频谱资源,并从复用频谱中进行射频能量采集,不能同时满足D2D设备高的射频能量采集需求和高数据传输需求。本文提出一对多的频谱复用方案,即单个D2D对复用多个蜂窝上行链路频谱通信,同时网络中的所有用户和设备作为分布式的射频能量来源对D2D接收端充电,即D2D接收端可采集全频段射频能量。针对以上场景提出的联合优化问题为非凸形式的混合整数非线性规划(mixed-integer nonlinear programming problem, MINLP)问题,难以用多项式时间算法获得最优解[15]。本文基于贪心思想和凸逼近理论提出两层资源分配算法对该优化问题进行求解。
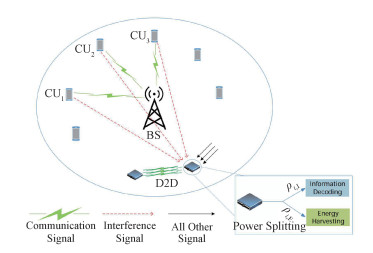
1 系统模型如图 1所示,单小区上行链路蜂窝网络中随机分布ND个D2D对(D2Di, i∈ΨD={1, 2, ⋯, ND})与NC个蜂窝用户(CUEj, j∈ΨC={1, 2, ⋯, NC}),蜂窝用户数量远大于D2D对数量,基站位于小区中心。假设系统中的所有设备均配备单个全向天线,蜂窝用户利用相互正交的频谱向基站发送数据,D2D对复用蜂窝上行链路频谱资源进行通信。考虑D2D接收端为能量受限设备且具备射频能量采集能力,D2Di接收端通过功率切片设备将接收到的全部射频信号按比例切分为两部分:ρi, I(0 < ρi, I < 1)部分用于信息解码;ρi, E(0 < ρi, E < 1)部分用于射频能量采集,且ρi, I+ρi, E=1。为同时满足D2D接收端高射频能量采集需求和高数据传输速率,允许单个D2D链路复用多个蜂窝上行链路频谱通信。为减小D2D对之间的同频干扰,每个蜂窝上行链路频谱最多只能被一个D2D链路复用。本文假设基站能够获得蜂窝小区范围内的所有信道状态信息。
|
Download:
|
| 图 1 系统模型 Fig. 1 System model | |
本文考虑D2D链路复用蜂窝上行链路频谱,与复用蜂窝下行链路频谱相比,复用蜂窝上行链路频谱时D2D接收端将收到更小的蜂窝同频干扰。参考D2D通信的相关研究[5, 14],本文忽略频率选择性衰落,假设D2D链路的小尺度衰落与复用哪些蜂窝上行链路频谱无关。因此D2D链路和蜂窝用户的传输速率可由香农公式表示为
| $ R_{d, i}=\sum\limits_{j=1}^{N_C} x_{i, j} \log \left(1+\frac{\rho_{i, I} p_{i, j} g_i}{\rho_{i, I} p_j g_{j, i}+n_{\mathrm{s}}}\right), $ | (1) |
| $ R_{c, j}=\log \left(1+\frac{p_j g_j}{\sum\limits_{i=1}^{N_D} x_{i, j} p_{i, j} g_{i, j}+n_{\mathrm{s}}}\right) . $ | (2) |
其中: 0~1变量xi, j∈{0, 1}表示D2D链路D2Di是否复用蜂窝用户CUEj的频谱,xi, j=1表示复用,xi, j=0表示不复用,且单个D2D链路可复用多个蜂窝上行链路频谱;pi, j表示D2Di复用CUEj所占用频谱的发射功率,pj表示CUEj的发射功率;gi和gj分别表示D2D链路和蜂窝上行链路的信道增益,包括路径损耗和小尺度瑞利衰落;ρi, I为功率切片因子,表示D2Di接收端将ρi, I比例的射频信号用于信息解码;ns表示信号处理噪声,由于信号处理噪声远大于天线噪声,因此表达式中忽略天线噪声;gj, i和gi, j分别表示CUEj和D2Di发射端对D2Di接收端和基站的干扰信道增益。
D2D接收端为能量受限设备且具备射频能量采集能力,因此D2Di接收端利用功率切片设备将全部射频信号的ρi, E比例用于射频能量采集,D2Di接收端采集到的射频能量可表示为
| $ E_{d, i}=\eta \rho_{i, E}\left(\sum\limits_{j=1}^{N_C} x_{i, j} p_{i, j} g_i+\sum\limits_{\substack{s \neq i \\ s \in \Psi_D}} \sum\limits_{j=1}^{N_C} x_{s, j} p_{s, j} g_{s, i}+\sum\limits_{j=1}^{N_C} p_j g_{j, i}\right). $ | (3) |
其中: η表示射频信号转化为电池能量的效率;0-1变量xs, j∈{0, 1}表示D2Ds(s≠i)是否复用CUEj的频谱;ps, j表示D2Ds(s≠i)在CUEj占用频谱上的发射功率;gs, i表示D2Ds(s≠i)发射端到D2Di接收端的信道增益。
多用户蜂窝网络中的SWIPT-D2D通信资源分配优化问题(P1)建立如下
| $ \text { P1: } \quad \max\limits _{X_{i, j}, v\left(\rho_{i, I}\right), v\left(\rho_{i, E}\right), P_{i, j}, P_j} \sum\limits_{i=1}^{N_D} R_{d, i}, $ | (4a) |
| $ \text { s. t. } R_{d, i} \geqslant R_d^{\mathrm{th}}, \;\forall i \in \Psi_D \text {, } $ | (4b) |
| $ \begin{array}{c} \log \left(1+\frac{\rho_{i, I} p_{i, j} g_i}{\rho_{i, I} p_j g_{j, i}+n_{\mathrm{s}}}\right) \geqslant R_{d, k}^{\mathrm{th}}, \\ \forall i \in \Psi_D, \quad \forall j \in \Psi_C, \end{array} $ | (4c) |
| $ E_{d, i} \geqslant E_d^{\mathrm{th}}, \;\forall i \in \Psi_D, $ | (4d) |
| $ R_{c, j} \geqslant R_c^{\mathrm{th}},\; \forall j \in \Psi_C, $ | (4e) |
| $ \begin{array}{c} 0 \leqslant \rho_{i, I} \leqslant 1, 0 \leqslant \rho_{i, E} \leqslant 1, \rho_{i, I}+\rho_{i, E} \leqslant 1, \\ \forall i \in \Psi_D, \end{array} $ | (4f) |
| $ \begin{array}{c} 0 \leqslant p_j \leqslant p_c^{\max }, \forall j \in \Psi_C, 0 \leqslant \sum\limits_{j=1}^{N_C} p_{i, j} \leqslant p_d^{\max }, \\ \forall i \in \Psi_D, \end{array} $ | (4g) |
| $ \sum\limits_{i=1}^{N_D} x_{i, j} \leqslant 1, x_{i, j} \in\{0, 1\}, \forall j \in \Psi_C . $ | (4h) |
其中(4a)为目标函数,表示D2D链路总速率,变量Xi, j, v(ρi, I), v(ρi, E), Pi, j, Pj为优化变量的向量表达形式;约束(4b)和(4e)为D2D对和蜂窝用户的最小速率约束;D2D对可复用多个蜂窝上行链路频谱,因此约束(4c)为D2D对通信子链路的最小速率约束;约束(4d)为D2D接收端的最小射频能量采集需求;约束(4f)为功率切片因子限制;约束(4g)表示D2D发射端和蜂窝用户的发射功率限制;(4h)为频谱复用约束,表示每个蜂窝上行链路频谱最多只能被一个D2D对复用。
2.2 问题求解优化问题(P1)中包含整数变量Xi, j和连续变量(v(ρi, I), v(ρi, E), Pi, j, Pj),同时目标函数与部分约束条件为非凸的log形式,因此(P1)为非凸形式的MINLP问题,难以求得最优解。本文提出两层资源分配算法:贪心比较资源分配(greedy-comparison resource allocation, GCRA)算法和基于连续凸逼近的外逼近(successive convex approximation-outer approximation, SCA-OA)算法。GCRA算法确定D2D对复用蜂窝上行链路频谱的数量;SCA-OA通过连续凸逼近将优化问题(P1)松弛为凸形式的MINLP,通过外部逼近将其分解为凸形式的非线性规划(nonlinear programming,NLP)问题和混合整数线性规划(mixed-integer linear programming, MILP)问题[16]。
GCRA算法通过贪心策略,逐个将频谱资源分配给增加复用一个数量蜂窝频谱能够使D2D总速率提升最多的D2D链路,直至D2D总速率不再增加或网络中没有剩余的频谱资源。分配频谱资源时,只考虑频谱资源的数量,无需考虑具体复用哪些蜂窝频谱。算法流程如表 1所示。
|
|
表 1 贪心比较资源分配算法 Table 1 Greedy-comparison resource allocation algorithm |
其中,Mi表示D2Di复用蜂窝频谱的个数;Y=[M1, M2, ⋯,MND]表示资源分配方案;Rd, sum(Y)表示Y条件下的D2D总速率;ΔRd, sum(Mi, Mi+1)表示D2Di复用蜂窝频谱数量由Mi增加到Mi+1后D2D总速率的变化。
GCRA算法确定了每个D2D对复用蜂窝上行链路频谱的个数,因此D2Di的第k个子通信子链路的传输速率表示为
| $ R_{d, i, k}=\log \left(1+\frac{\rho_{i, I} p_{i, k} g_i}{\sum\limits_{j=1}^{N_C} x_{i, k, j} \rho_{i, I} p_j g_{j, i}+n_{\mathrm{s}}}\right). $ | (5) |
D2Di的传输速率和D2D总速率分别表示为
| $ R_{d, i}=\sum\limits_{k=1}^{M_i} R_{d, i, k}, $ | (6) |
| $ R_{d, \mathrm{sum}}=\sum\limits_{i=1}^{N_D} \sum\limits_{k=1}^{M_i} R_{d, i, k} . $ | (7) |
CUEj的传输速率和D2Di的射频能量采集表示为
| $ R_{c, j}=\log \left(1+\frac{p_j g_j}{\sum\limits_{i=1}^{N_D} \sum\limits_{k=1}^{M_i} x_{i, k, j} p_{i, k} g_{i, j}+n_{\mathrm{s}}}\right), $ | (8) |
| $ E_{d, i}=\eta \rho_{i, E}\left(\sum\limits_{k=1}^{M_i} p_{i, k} g_i+\sum\limits_{\substack{s \neq i \\ s \in \Psi_D}} \sum\limits_{k=1}^{M_s} p_{s, k} g_{s, i}+\sum\limits_{j=1}^{N_C} p_j g_{j, i}\right) . $ | (9) |
其中: 0-1变量xi, k, j∈{0, 1}表示D2Di的第k个子通信链路是否复用CUEj的频谱;pi, k和ps, k分别表示D2Di和D2Ds(s≠i)在第k个子通信链路上的发射功率;Mi和Ms分别表示D2Di和D2Ds(s≠i)复用蜂窝频谱的个数。根据式(5)~式(9)原始优化问题(P1)转化为优化问题(P2)
| $ \text { P2: } \max\limits _{X_{i, k, j}, v\left(\rho_{i, I}\right), v\left(\rho_{i, E}\right), P_{i, k}, P_j} R_{d, \mathrm{sum}} , $ | (10a) |
| $ \text { s.t. }(4 \text{b}), (4 \text{d}) \sim(4 \text{f}), $ | (10b) |
| $ R_{d, i, k} \geqslant R_{d, k}^{\mathrm{th}}, \forall i \in \Psi_D, \forall k \in \mathrm{M}_i, $ | (10c) |
| $ \begin{array}{c} 0 \leqslant p_j \leqslant p_c^{\max }, \forall j \in \Psi_C, \\ 0 \leqslant \sum\limits_{k=1}^{M_i} p_{i, k} \leqslant p_d^{\max }, \forall i \in \Psi_D, \end{array} $ | (10d) |
| $ \sum\limits_{i=1}^{N_D} \sum\limits_{k=1}^{M_i} x_{i, k, j} \leqslant 1, x_{i, k, j} \in\{0, 1\}, \forall j \in \Psi_c . $ | (10e) |
由于(P2)为非凸形式,通过变量替换和连续凸逼近对(P2)进行凸松弛。首先进行变量替换,令
| $ \alpha \log \left(z_0\right)+\beta \leqslant \log \left(1+z_0\right) . $ | (11) |
在满足如下条件时,式(11)在z=z0时等号成立
| $ \left\{\begin{array}{l} \alpha=\frac{z_0}{\left(1+z_0\right)}, \\ \beta=\log \left(1+z_0\right)-\alpha \log \left(z_0\right). \end{array}\right. $ | (12) |
D2Di第k个子通信链路传输速率可表示为
| $ \begin{array}{c} R_{d, i, k}=\alpha_{d, i, k}\left(\log \left(g_i\right)+\hat{\rho}_{i, I}+\hat{p}_{i, k}-\right.\\ \left.\left(\log \left(\sum\limits_{j=1}^{N_C} x_{i, k, j} \mathrm{e}^{\hat{\rho}_{i, I}+\hat{p}_j} g_{j, i}+n_s\right)\right)\right)+\beta_{d, i, k}. \end{array} $ | (13) |
CUEj的传输速率可表示为
| $ \begin{array}{c} R_{c, j}=\alpha_{c, j}\left(\log \left(g_j\right)+\hat{p}_j-\right. \\ \left.\left(\log \left(\sum\limits_{i=1}^{N_D} \sum\limits_{k=1}^{M_i} x_{i, k, j} e^{\hat{p}_{i, k}} g_{i, j}+n_s\right)\right)\right)+\beta_{c, j}. \end{array} $ | (14) |
优化问题(P2)经变量替换后,射频能量采集约束仍为非凸约束,对其在(
| $ \begin{array}{c} E_{d, i}=E_{d, i}\left(v\left(\hat{\rho}^*\right), \hat{P}^*\right)+\nabla E_{d, i}\left(v\left(\hat{\rho}^*\right), \hat{P}^*\right)^{\mathrm{T}} \times \\ \left(\begin{array}{l} v(\hat{\rho})-v\left(\hat{\rho}^*\right) \\ \hat{P}-\hat{P}^* \end{array}\right) . \end{array} $ | (15) |
外部逼近算法将经过以上变换的的优化问题(P2)分解为NLP问题和MILP问题。当0~1变量Xi, k, j固定为Xi, k, jζ时,由式(6)、式(7)、式(13)~式(15)得到凸形式的NLP优化问题(P2.1)
| $ \begin{array}{c} {\rm{ P2}}{\rm{. 1: }}\\ \mathop {\min }\limits_{\begin{array}{*{20}{l}} {v\left( {{{\hat \rho }_{i, I}}} \right), v\left( {{{\hat \rho }_{i, E}}} \right)}\\ {{{\hat P}_{i, k}}, {{\hat P}_j}, X_{i, k, \mathit{j}}^\zeta } \end{array}} - {R_{d, {\rm{sum}}}}\left( {v\left( {{{\hat \rho }_{i, I}}} \right), v\left( {{{\hat \rho }_{i, E}}} \right), {{\hat P}_{i, k}}, {{\hat P}_j}, X_{i, k, j}^\zeta } \right), \end{array} $ | (16a) |
| $ \text { s.t. }(4 \text{b}), (4 \text{d}), (4 \text{e}), (10 \text{c}), $ | (16b) |
| $ \mathrm{e}^{\hat{\rho}_{i, I}} \leqslant 1, \mathrm{e}^{\hat{\rho}_{i, E}} \leqslant 1, \mathrm{e}^{\hat{\rho}_{i, I}}+\mathrm{e}^{\hat{\rho}_{i, E}} \leqslant 1, \forall i \in \Psi_D, $ | (16c) |
| $ \mathrm{e}^{\hat{p}_j} \leqslant p_c^{\max }, \forall j \in \Psi_C, \sum\limits_{k=1}^{M_i} \mathrm{e}^{\hat{p}_{i, k}} \leqslant p_d^{\max }, \forall i \in \Psi_D . $ | (16d) |
根据优化问题(P2.1)得到的解和式(15)得到MILP优化问题(P2.2)
| $ \text { P2. 2: } \min\limits _{x_{i, k, j} v\left(\hat{\rho}_{i, I}\right), v\left(\hat{\rho}_{i, E}\right), \hat{P}_{i, k}, \hat{P}_j, \theta} \theta \text {, } $ | (17a) |
| $ \text { s.t. }(4 \mathrm{d}), (10 \mathrm{e}), \mathrm{e}^{\hat{p}_j} \leqslant p_c^{\max }, \forall j \in \Psi_C \text {, } $ | (17b) |
| $ f_1\left(\hat{P}^*\right)+\nabla f_1\left(\hat{P}^*\right)^{\mathrm{T}} \times\left(\hat{P}-\hat{P}^*\right) \leqslant 0, \forall i \in \Psi_D, $ | (17c) |
| $ \begin{array}{c} f_2\left(v\left(\hat{\rho}^*\right)\right)+\nabla f_2\left(v\left(\hat{\rho}^*\right)\right)^{\mathrm{T}} \times \\ \left(v(\hat{\rho})-v\left(\hat{\rho}^*\right)\right) \leqslant 0, \forall i \in \Psi_D, \end{array} $ | (17d) |
| $ \begin{array}{c} -R_{d, \mathrm{sum}}\left(v\left(\hat{\rho}^*\right), \hat{P}^*, X^{\xi}\right)- \\ \nabla R_{d, \mathrm{sum}}\left(v\left(\hat{\rho}^*\right), \hat{P}^*, X^{\xi}\right)^{\mathrm{T}} \times\\ \left(\begin{array}{l} v(\hat{\rho})-v\left(\hat{\rho}^*\right) \\ \hat{P}-\hat{P}^* \\ X-X^{\xi} \end{array}\right)-\theta \leqslant 0, \end{array} $ | (17e) |
| $ \begin{array}{c} R_d^{\mathrm{th}}-R_{d, i}\left(v\left(\hat{\rho}^*\right), \hat{P}^*, X^{\xi}\right)- \\ \nabla R_{d, i}\left(v\left(\hat{\rho}^*\right), \hat{P}^*, X^{\xi}\right)^{\mathrm{T}} \times \\ \left(\begin{array}{l} v(\hat{\rho})-v\left(\hat{\rho}^*\right) \\ \hat{P}-\hat{P}^* \\ X-X^{\xi} \end{array}\right) \leqslant 0, \forall i \in \Psi_D, \end{array} $ | (17f) |
| $ \begin{array}{c} R_{d, k}^{\mathrm{th}}-R_{d, i, k}\left(v\left(\hat{\rho}^*\right), \hat{P}^*, X^{\xi}\right)- \\ \nabla R_{d, i, k}\left(v\left(\hat{\rho}^*\right), \hat{P}^*, X^{\xi}\right)^{\mathrm{T}} \times \\ \left(\begin{array}{l} v(\hat{\rho})-v\left(\hat{\rho}^*\right) \\ \hat{P}-\hat{P}^* \\ X-X^{\xi} \end{array}\right) \leqslant 0, \forall i \in \Psi_D, \forall k \in \mathrm{M}_i, \end{array} $ | (17g) |
| $ \begin{array}{c} R_c^{\mathrm{th}}-R_{c, j}\left(\hat{P}^*, X^{\xi}\right)-\nabla R_{c, j}\left(\hat{P}^*, X^{\xi}\right)^{\mathrm{T}} \times \\ \left(\begin{array}{c} \hat{P}-\hat{P}^* \\ X-X^{\xi} \end{array}\right) \leqslant 0, \forall j \in \Psi_C . \end{array} $ | (17h) |
为方便表示,优化问题(P2.2)中用符号
|
|
表 2 外部逼近算法 Table 2 Approximation-outer approximation algorithm |
考虑半径为200 m的单小区蜂窝网络,基站位于小区的中心,SWIPT-D2D设备和蜂窝用户理想均匀的分布在小区内部。表 3给出了仿真参数设置[2, 18]。
|
|
表 3 仿真参数 Table 3 Simulation parameters |
为验证所提方案与算法的性能,选择以下资源分配策略和算法进行对比:D2D通信一对一频谱匹配策略;D2D接收端分配相同功率切片因子策略;基于优先级的序列算法[19] (priority-based sequential algorithm, PBSA)。
图 2(a)和2(b)分别为低D2D通信速率需求(0.6 Mbit/s)和高D2D通信速率需求(1.4 Mbit/s)时,D2D接收端射频能量采集需求对D2D平均速率的影响。由图 2可知,在所有资源分配策略与算法中,随着D2D接收端射频能量采集需求增高,D2D平均速率逐渐降低,且下降趋势越来越快。这是由于基站对D2D接收端功率切片的控制,将射频信号中更高的比例ρi, E用于能量采集,更少的比例ρi, I用于信息解码,导致D2D平均速率逐渐减小;同时随着D2D射频能量采集需求变高,射频能量主要来源蜂窝用户的发射功率变大,D2D设备的受到的同频干扰增大,平均速率下降。随着ρi, I的减小,信号处理噪声ns对D2D速率的影响越来越明显,因此D2D平均速率下降速度随D2D射频能量采集需求增高而变快。

|
Download:
|
| 图 2 D2D射频能量采集需求与D2D平均速率关系 Fig. 2 D2D radio frequency energy harvesting requirement versus D2D average rate | |
在传统一对一频谱匹配策略中,当D2D通信速率需求较低时(0.6 Mbit/s),如图 2(a)中所示,D2D设备能够满足低能量需求下的信息传输,但D2D平均速率较低;当D2D通信速率需求变高时(1.4 Mbit/s),如图 2(b)所示,D2D平均速率无法达到D2D最小速率需求。本文所提算法,在低D2D通信速率需求下(0.6 Mbit/s)能够满足高能量采集需求,当D2D通信速率需求达到1.4 Mbit/s时,仍可满足3 mW以上的能量采集需求。综合可知,所提算法能够使D2D接收端在高射频能量采集需求下维持高的信息解码速率。与相同功率切片策略相比,所提算法在提升D2D平均速率方面效果显著,这是由于在多用户网络中,每个D2D对的信道质量和射频能量采集能力不同,为所有D2D接收端分配相同功率切片系数会降低D2D最优传输速率。在相同射频能量采集需求下,所提算法比PBSA得到的D2D平均速率更高,原因是PBSA在频谱分配过程中是静态的,且分配过程仅保证每个D2D对速率的局部最优,所提算法能够保证分配每个频谱资源时,都能使D2D通信的总速率提升最大,考虑了全局最优。
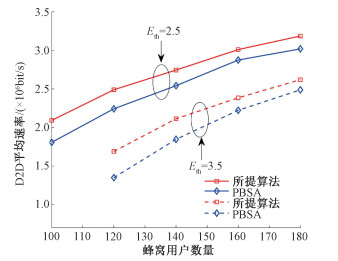
图 3为系统中蜂窝用户数量对D2D平均速率的影响。所提算法与PBSA在不同射频能量采集需求下的D2D平均速率都随蜂窝用户数量的增加逐渐增大。原因是,随着蜂窝用户数量的增加,D2D对之间的频谱资源竞争降低,D2D对可分配到同频干扰更低,数量更多的蜂窝频谱资源进行通信。
|
Download:
|
| 图 3 蜂窝用户数量与D2D平均速率关系(Rdth=1 Mbit/s) Fig. 3 Number of cellular users versus D2D average rate(Rdth=1 Mbit/s) | |
同时,蜂窝用户的发射功率较D2D发射端更大,蜂窝用户数量的增加,使得D2D接收端可得到的射频能量来源更加充足。因此使得在相同射频能量采集需求下,D2D平均速率随蜂窝用户数量的增加逐渐增大。
4 结束语本文研究蜂窝网络下的SWIPT-D2D通信的资源分配问题。针对当前D2D通信一对一频谱复用策略无法满足D2D接收端高射频能量采集需求和高数据传输需求的现状,提出一对多的频谱复用方案,允许D2D接收端采集全频段射频能量,充分利用射频资源。提出两层资源分配算法GCRA和SCA-OA解决提出的非凸形式的MINLP问题。仿真表明,所提算法与其他资源分配策略相比,在满足用户设备能量和速率需求条件下显著提升了D2D通信总速率。
| [1] |
Wang C X, Haider F, Gao X Q, et al. Cellular architecture and key technologies for 5G wireless communication networks[J]. IEEE Communications Magazine, 2014, 52(2): 122-130. Doi:10.1109/MCOM.2014.6736752 |
| [2] |
Li R Z, Hong P L, Xue K P, et al. Energy-efficient resource allocation for high-rate underlay D2D communications with statistical CSI: a one-to-many strategy[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 4006-4018. Doi:10.1109/TVT.2020.2973228 |
| [3] |
Sawyer N, Smith D B. Flexible resource allocation in device-to-device communications using stackelberg game theory[J]. IEEE Transactions on Communications, 2019, 67(1): 653-667. Doi:10.1109/TCOMM.2018.2873344 |
| [4] |
李维谦, 邱玲. 支持D2D多播的蜂窝网络分簇策略与资源分配[J]. 中国科学院大学学报, 2019, 36(1): 137-143. Doi:10.7523/j.issn.2095-6134.2019.01.019 |
| [5] |
Luo Y, Hong P L, Su R L, et al. Resource allocation for energy harvesting-powered D2D communication underlaying cellular networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(11): 10486-10498. Doi:10.1109/TVT.2017.2727144 |
| [6] |
Sakr A H, Hossain E. Cognitive and energy harvesting-based D2D communication in cellular networks: stochastic geometry modeling and analysis[J]. IEEE Transactions on Communications, 2015, 63(5): 1867-1880. Doi:10.1109/TCOMM.2015.2411266 |
| [7] |
Liu Y W, Wang L F, Raza Zaidi S A, et al. Secure D2D communication in large-scale cognitive cellular networks: a wireless power transfer model[J]. IEEE Transactions on Communications, 2016, 64(1): 329-342. Doi:10.1109/TCOMM.2015.2498171 |
| [8] |
Ponnimbaduge Perera T D, Jayakody D N K, Sharma S K, et al. Simultaneous wireless information and power transfer (SWIPT): recent advances and future challenges[J]. IEEE Communications Surveys & Tutorials, 2018, 20(1): 264-302. Doi:10.1109/COMST.2017.2783901 |
| [9] |
Lu X, Wang P, Niyato D, et al. Wireless networks with RF energy harvesting: a contemporary survey[J]. IEEE Communications Surveys & Tutorials, 2015, 17(2): 757-789. Doi:10.1109/COMST.2014.2368999 |
| [10] |
Lim D W, Kang J, Kim H M. Adaptive power control for D2D communications in downlink SWIPT networks with partial CSI[J]. IEEE Wireless Communications Letters, 2019, 8(5): 1333-1336. Doi:10.1109/LWC.2019.2916352 |
| [11] |
Lim D W, Kang J, Chun C J, et al. Joint transmit power and time-switching control for device-to-device communications in SWIPT cellular networks[J]. IEEE Communications Letters, 2019, 23(2): 322-325. Doi:10.1109/LCOMM.2018.2883432 |
| [12] |
Huang J, Xing C C, Guizani M. Power allocation for D2D communications with SWIPT[J]. IEEE Transactions on Wireless Communications, 2020, 19(4): 2308-2320. Doi:10.1109/TWC.2019.2963833 |
| [13] |
Huang J, Cui J J, Xing C C, et al. Energy-efficient SWIPT-empowered D2D mode selection[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 3903-3915. Doi:10.1109/TVT.2020.2970235 |
| [14] |
Zhou Z Y, Gao C X, Xu C, et al. Energy-efficient stable matching for resource allocation in energy harvesting-based device-to-device communications[J]. IEEE Access, 2017, 5: 15184-15196. Doi:10.1109/ACCESS.2017.2678508 |
| [15] |
Palomar D P, Chiang M. A tutorial on decomposition methods for network utility maximization[J]. IEEE Journal on Selected Areas in Communications, 2006, 24(8): 1439-1451. Doi:10.1109/JSAC.2006.879350 |
| [16] |
Fletcher R, Leyffer S. Solving mixed integer nonlinear programs by outer approximation[J]. Mathematical Programming, 1994, 66(1): 327-349. Doi:10.1007/BF01581153 |
| [17] |
Papandriopoulos J, Evans J S. SCALE: a low-complexity distributed protocol for spectrum balancing in multiuser DSL networks[J]. IEEE Transactions on Information Theory, 2009, 55(8): 3711-3724. Doi:10.1109/TIT.2009.2023751 |
| [18] |
Ng D W K, Lo E S, Schober R. Wireless information and power transfer: energy efficiency optimization in OFDMA systems[J]. IEEE Transactions on Wireless Communications, 2013, 12(12): 6352-6370. Doi:10.1109/TWC.2013.103113.130470 |
| [19] |
Mach P, Becvar Z, Najla M. Resource allocation for D2D communication with multiple D2D pairs reusing multiple channels[J]. IEEE Wireless Communications Letters, 2019, 8(4): 1008-1011. Doi:10.1109/LWC.2019.2903798 |
 2022, Vol. 39
2022, Vol. 39 


