随着信息化程度的不断提升,在岩体工程中利用数值模拟技术对岩体进行力学计算与分析,对预防地质灾害的意义和价值越来越大。然而对岩体进行精确的三维重建是对岩体进行后续分析的基础,因此如何获取完整的岩体地表信息对岩体重建至关重要。
三维激光扫描是获取岩体三维信息的重要设备,但由于扫描环境以及测量范围的限制,对于大型岩体,往往不能通过一次扫描而获得全部的场景,需要在不同的视角对岩体进行多站扫描,而将多个视角获得的岩体点云数据融合成一个点云数据是岩体点云配准的主要工作。因此,点云配准是三维数据处理中关键的步骤之一,也是后续进行点云数据应用的基础。
点云配准作为计算机视觉的基本问题,近年来,随着研究人员深入的研究,取得了很多成果,其中最为常用的方法是迭代最近点算法[1](iterative closest point,ICP)。ICP算法是通过迭代的思想,每次迭代使目标点云与源点云距离最小,不用寻找特征描述子,只需要优化一个目标函数,并使算法收敛。虽然这种算法简单,但是初始位置以及噪声点对该算法影响很大,容易陷入局部最优,最终导致配准失败。王飞鹏等[2]提出基于高斯曲率的改进算法,通过高斯曲率过滤掉部分点云,将剩余的点云应用ICP算法进行配准,改善了ICP算法的效率。
此外,还有许多基于对应特征点的算法被提出,这类算法是寻找源点云与目标点云中的对应点对,通过这些对应的点对来计算点云变换参数。例如,Aiger等[3]提出的四点法(4-points congruent sets,4PCS)是一种基于刚体变换比例不变量的算法,利用刚体变换不会改变两点的距离以及交叉点的对应比例的性质;Yang和Zang[4]提出基于曲线的配准方法,通过提取点云中的曲线进行配准;Xian等[5]提出一个通过将三维无序点云转换为二维数字图像的方法,在二维图像中通过尺度不变特征变换(scale invariant feature transform,SIFT)算法提取特征点进行配准;Wang等[6]提出基于高斯曲率的N阶完全图算法,通过选择高斯曲率较大的点构造一个N阶完全图的特征描述子进行匹配;Hu等[7]利用岩体点云表面大部分为平面的特点,通过提取岩体点云的平面进行配准;Biber和StraBer[8]提出一种三维正态分布变换算法(3D-normal distribution transform,3 D-NDT),利用点云表面点分布的统计信息以及迭代更新的策略实现配准。
近几年,由于机器学习方法的兴起,一些基于机器学习的点云配准算法被提出。Vongkulbhisal等[9]提出一种判别优化方法(discriminative optimization,DO),该方法与传统构建损失函数和求解损失函数不同,它通过学习一个矩阵的更新序列求解损失函数从而得到最终的变换;Elbaz等[10]提出一种用自编码器进行局部定位的算法(localization by registration using a deep auto-encoder reduced cover set,LORAX),该算法通过将分割的点云投影成为深度图,再通过自编码器构造一个特征描述子进行配准;Lu等[11]提出一种通过端到端的神经网络寻找匹配点进行配准的方法;舒程珣等[12]提出通过基于图像的卷积神经网络进行配准的算法;刘鸣等[13]提出一种基于独立成分分析的配准方法, 该方法通过提取源点云与目标点云的独立成分进行点云配准。
然而岩体点云不同于一般的点云,具有密度大、数据量大,且大部分区域为平面等特点,使得一些常用的点云配准算法不能满足岩体点云配准的精度要求。本文基于岩体点云表面大部分区域为平面的特点,并根据岩体工程对于精度的较高要求,提出一种基于几何特征逐层过滤的岩体点云配准算法。该方法通过高斯曲率过滤掉绝大部分点云,再通过主曲率、主方向、法向量、邻域的协方差矩阵的特征值和特征向量等进行匹配点对的层层筛选,进而准确地找到对应的匹配点对计算变换参数,最后利用ICP算法进行精配准。算法具有较高的精度。
1 背景知识点云配准即是将源点云与目标点云融合在一起,设源点云为P,目标点云为Q,则可将点云配准抽象为:P经过刚体变换,变换到Q的坐标系下,即
| $ \boldsymbol{Q}=\boldsymbol{RP}+\boldsymbol{T}. $ | (1) |
其中: R为一个正交矩阵,T为平移向量。点云配准的主要工作就是计算R和T,如果求出2个点云中的匹配点对,则可以通过解一个方程组求出R和T,其中方程组为:
| $ \begin{aligned} &\boldsymbol{x}_{1}^{1}=\boldsymbol{R} \boldsymbol{x}_{1}+\boldsymbol{T} \\ &\boldsymbol{x}_{2}^{1}=\boldsymbol{R} \boldsymbol{x}_{2}+\boldsymbol{T} . \\ &\boldsymbol{R} \boldsymbol{R}^{\mathrm{T}}=\boldsymbol{I} \end{aligned} $ | (2) |
其中:
| $ \begin{aligned} \min & \sum\limits_{i=1}^{N}\left\|\boldsymbol{x}_{i}^{1}-\left(\boldsymbol{R} \boldsymbol{x}_{i}+\boldsymbol{T}\right)\right\|^{2} \\ \text {s. t. } & \boldsymbol{R} \boldsymbol{R}^{\mathrm{T}}=\boldsymbol{I} \end{aligned}. $ | (3) |
其中:
对于一个曲面,经过刚体变换之后,部分几何特征不会发生变化,而部分几何特征会发生有规律的变化。可以通过这些不变的几何特征以及有规律变化的几何特征进行匹配点的筛选,从而进行配准。其中曲率作为刚体变换的不变量,可以用来筛选初始匹配点对。对于一个点云中的点变换到其对应点,该点与其对应点的邻域的协方差矩阵相似,从而可以通过判断邻域协方差矩阵是否相似进一步筛选对应的匹配点。如果2个点互为对应点,则可以通过计算各自的协方差矩阵的特征向量矩阵来计算旋转矩阵。而曲面的法向量和主方向经过刚体变换之后,也会发生相应的旋转,则可以利用法向量和主方向进一步筛选。
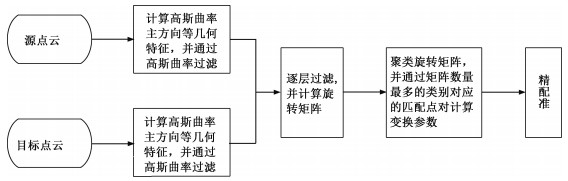
2 基于匹配点逐层过滤的岩体点云配准算法基于对于岩体点云密度大、数量大以及岩体表面大部分为区域平面的特点,提出基于几何特征逐层过滤的岩体点云配准算法,该算法通过几何特征来筛选匹配点对以完成粗配准,最后用ICP算法进行精配准,算法框图如图 1所示。
|
Download:
|
| 图 1 算法流程图 Fig. 1 Algorithm flowchart | |
该算法包括4个主要步骤:1)计算高斯曲率等几何特征,通过高斯曲率过滤源点云与目标点云;2)逐层过滤匹配点对;3)矩阵聚类;4)ICP精配准。下面介绍算法的关键步骤。
2.1 几何特征的计算点云的高斯曲率通过该点的邻域点进行计算。本文通过Zhang等[14]提出的算法计算高斯曲率。该算法计算点x的主曲率是通过该点的邻域{x1, x2, …, xN}来计算。在计算出主曲率的同时,还计算了对应的主方向以及法向量。最终通过k=k1×k2求出高斯曲率。该算法计算高斯曲率大小与邻域大小有关,几何特征计算受点云表面噪声点影响较大,选取邻域较大,则高斯曲率计算通常偏小,且耗时较多,但是鲁棒性较强;选取邻域较小,高斯曲率计算偏大,耗时较小,鲁棒性较弱。对于配准来说,如果噪声较大,则应该选择较大的邻域进行计算,这样鲁棒性较强,噪声较小,选择较小的邻域进行计算,邻域大小的选择应该根据点云的具体情况而定。一般而言,设置邻域大小为100个点有较强的鲁棒性,能够得到较好的结果。
2.2 几何特征逐层过滤由于岩体表面大部分区域为平面区域或接近平面区域,岩体点云大部分点的高斯曲率为零或接近零,可以通过选取高斯曲率较大的点进行配准,这样不用选择全部的点参与配准,通过设置一个区间,过滤掉高斯曲率不在这个区间的点,在剩余的点中选择匹配点。对于剩余的点云中的点,利用主曲率进行对应点的初次匹配,对于点云中的每个点,可以找到一些与其主曲率相同的点。设点x的主曲率为
| $ \left|k_{1}^{0}-k_{1}^{1}\right|+\left|k_{2}^{0}-k_{2}^{1}\right|<\varepsilon_{k}, $ | (4) |
则其主曲率相同,但其邻域结构可能不相同,若2个点是对应点,则其邻域一定相同,所以再通过判断对应点对x, x1的协方差矩阵M, M1是否相似来验证对应点对的邻域是否对应,设λ10,λ20,λ30为M的特征值,λ11,λ21,λ31为M1的特征值,若满足
| $ \left|\lambda_{1}^{0}-\lambda_{1}^{1}\right|+\left|\lambda_{2}^{0}-\lambda_{2}^{1}\right|+\left|\lambda_{3}^{0}-\lambda_{3}^{1}\right|<\varepsilon_{\lambda}, $ | (5) |
则矩阵相似,可以利用公式R=P1PT计算其旋转矩阵,其中P, P1分别为M, M1的特征向量矩阵。如果R为源点云与目标点云的旋转矩阵,则可以引入法向量与主方向继续筛选,设n与n1分别为x与x1的法向量,v1,v2和v11,v21分别为x与x1对应的主方向。如果R满足‖n1-Rn‖<εn,则继续验证‖v11-Rv1‖<εv1,‖v21-Rv2‖<εv2是否满足,如果满足,则可认为x与x1存在对应关系,最后保存该旋转矩阵。
2.3 矩阵聚类以及精配准阶段前面的步骤可以得到很多匹配的对应点对,但是有的点对不是真正的对应点对,需要进行筛选。前面步骤求出的大部分矩阵应该符合源点云到目标点云的变换,少部分矩阵不符合该刚体变换,则可以对符合条件的矩阵进行聚类,将矩阵数量最多的类别的对应点对通过最小二乘法求出刚体变换的参数。目前,主流的精配准算法为ICP算法,将算法前面阶段计算的旋转矩阵和平移向量作为ICP算法的初始值进行迭代优化,最终得到更精确的结果。
3 算法分析与比较为了测试算法的鲁棒性,分别在不同强度高斯噪声、不同初始位置、不同重合度的条件下进行实验。为了比较算法性能,用ICP算法和Wang等[6]提出的基于N阶完全图的算法(N-point complete graphs,NCG)进行对比实验,其中ICP算法是在点云库[15](point cloud library,PCL)中实现。本文在公共数据集RockBench[16]和在北京香山公园采集的数据上进行实验。其中利用RockBench中的3个点云数据,为数据1、数据2、数据3,在香山公园中采集的数据为数据4、数据5、数据6,分别为不同角度采集的数据。实验中通过计算根均方差(root mean square,RMS)衡量算法精度。其中RMS公式为
| $ \mathrm{RMS}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{i}^{1}\right\|^{2}}. $ | (6) |
其中:N为配准点云覆盖部分的点数量,xi与xi1为源点云与目标点云配准之后的对应点。实验部分首先进行鲁棒性检测,分别在不同高斯噪声、不同初始位置及不同重合度下进行实验,然后进行对比实验,对比实验分别在公开数据集和香山数据上进行。
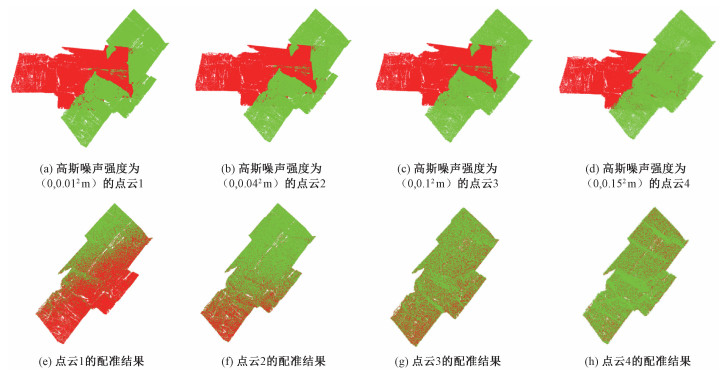
3.1 鲁棒性检测实验鲁棒性检测分为对噪声、初始位置和重合度的鲁棒性检测。对于噪声的鲁棒性检测是对源点云中的每个点替换成不同强度的高斯噪声点,再将该点云变换到另一位置,成为该点云对应的目标点云,其中高斯噪声的强度分别为(0,0.012 m),(0,0.042 m),(0,0.12 m),(0,0.152 m),源点云和目标点云的初始位置以及匹配结果如图 2所示。
|
Download:
|
| 图 2 噪声鲁棒性实验结果 Fig. 2 Result of noise robustness test | |
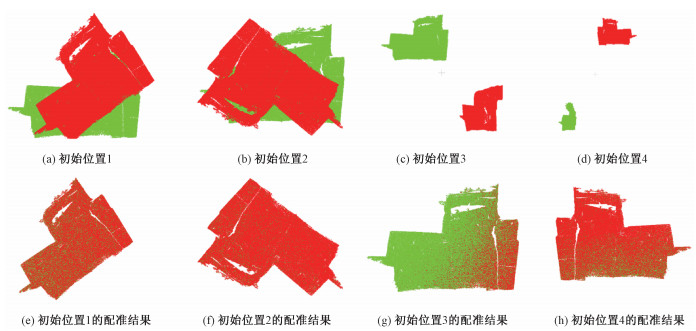
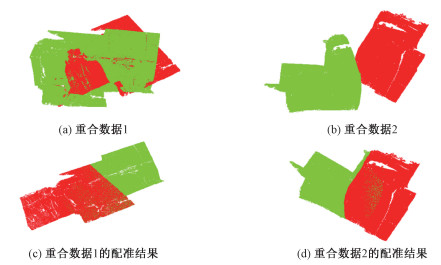
对于初始位置鲁棒性检测,是将点云变换到不同的位置进行匹配,源点云和目标点云的初始位置以及匹配结果如图 3所示。对于不同重合度的鲁棒性检测,是在两组部分重叠的点云上进行实验,第1组点云重叠的点数为63 785,其中源点云中有118 230个点,目标点云中有201 738个点。第2组点云重叠的点的个数为42 151,其中源点云中有185 308个点,目标点云有164 143个点,源点云和目标点云的初始位置以及匹配结果如图 4,配准RMS如表 1所示。
|
Download:
|
| 图 3 不同初始位置的配准结果 Fig. 3 Registration results for different initial positions | |
|
Download:
|
| 图 4 不同重合度配准结果 Fig. 4 Registration results with different degrees of coincidence | |
|
|
表 1 鲁棒性测试RMS Table 1 RMS of robustness test |
从图 2、图 3、图 4及表 1可以看出,初始位置对算法无影响,不同的重叠率对算法无影响,在存在高斯噪声的情况下,算法比较稳定,在高斯噪声较小的情况下,算法有较高的精度。
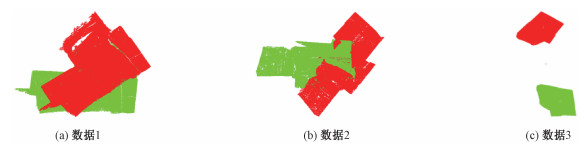
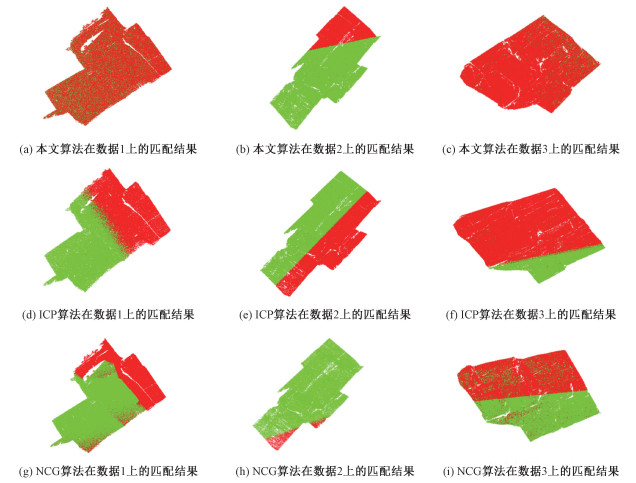
3.2 算法对比实验本文对比实验包括ICP算法、NCG算法,以及本文提出的经过ICP精配准的算法和未经过ICP精配准的算法,并通过计算RMS比较算法精度。分别在RockBench数据集中的数据1、数据2、数据3和在北京香山公园采集的数据4、数据5、数据6中进行了对比实验。实验数据的基本信息如表 2所示。数据1、数据2、数据3的初始位置如图 5,目标点云是通过对源点云进行变换得到,数据1、数据2、数据3的配准结果如图 6所示,RMS如表 3所示。数据4、数据5、数据6的初始位置如图 7所示,配准RMS如表 4所示,配准结果如图 8所示。
|
|
表 2 点云数据基本信息 Table 2 Information of point cloud data |
|
Download:
|
| 图 5 数据1、数据2、数据3初始位置 Fig. 5 Initial position of Data1, Data2, and Data3 | |
|
Download:
|
| 图 6 数据1、数据2、数据3匹配结果 Fig. 6 Registration result of Data1, Data2, and Data3 | |
|
|
表 3 数据1、数据2、数据3的RMS Table 3 RMS of Data1, Data2, and Data3 |

|
Download:
|
| 图 7 数据4、数据5、数据6的初始位置 Fig. 7 Initial position of Data4, Data5, and Data6 | |
|
|
表 4 香山公园数据的RMS Table 4 RMS of Xiangshan data registration results |

|
Download:
|
| 图 8 算法在数据4、数据5、数据6的匹配结果 Fig. 8 Registration results of Data4, Data5, and Data6 | |
由表 3可知,ICP算法和NCG算法在理想的情形下精度很高,而本文提出的算法精度能够与ICP算法和NCG算法媲美。由表 4可以看出,本文的算法在香山的3个岩石数据上表现都很稳定,本文的粗配准算法和经过精细配准的算法精度相差很小,而且本文粗配准算法在精度上比其他2种算法要高。ICP算法由于存在局部最优的问题,导致ICP在数据4和数据6上未匹配成功。而NCG算法在3个点云数据上虽然都匹配成功,但是精度都没有本文未经过ICP精配准的算法精度高。根据实验可知,本算法能够有效避免初始位置对算法的影响。在筛选匹配点对的过程中,本算法是通过匹配邻域来匹配对应点,这使得算法对噪声比较鲁棒,而且算法是通过几何特征逐层筛选匹配点对,最终能够剔除误匹配点对,从而得到精确的匹配点对。
3.3 运行时间分析本文算法总体时间主要分为4部分:Tg表示计算高斯曲率等几何特征的时间复杂度,Tr表示逐层过滤筛选匹配点对的时间复杂度,Tc表示矩阵聚类的时间复杂度,Ticp表示精配准的时间复杂度。这里,
| $ T_{g}=O(n \log n+m \log m), $ | (7) |
其中:m,n分别为源点云与目标点云的数量。Tr=O(K1K2),其中K1,K2分别为源点云与目标点云过滤之后剩余的点云的数量。Tc=O(K32),其中K3为矩阵的数量。一般来说,K1,K2,K3相对于源点云与目标点云的数量较小。Ticp=O(m log n)。则总时间复杂度为
| $ T=T_{g}+T_{r}+T_{c}+T_{\mathrm{icp}}. $ | (8) |
若选取合适的参数,可以使K1,K2,K3较小,最终使得
| $ T \approx O(N \log N). $ | (9) |
其中,N=max(m, n)。
对于NCG算法,若选取合适的参数,可使NCG算法时间复杂度为:TNCG≈O(N log N),其中,N=max(m, n)。
ICP算法时间复杂度为:Ticp=O(m log n)。因此当源点云与目标点云的数量相差不大时,3个算法的时间复杂度相近。
4 总结本方法针对岩体点云的数据量大、密度大,大部分区域为平面的特点,提出一种基于几何特征逐层过滤的岩体点云配准算法,该算法通过高斯曲率过滤掉绝大部分点云,再通过主曲率、主方向、法向量、邻域的协方差矩阵的特征值和特征向量逐层筛选匹配点对,最终精确地找到匹配点对。实验结果表明,本文算法能够很好地匹配岩体点云,对于初始位置和高斯噪声都具有较好的鲁棒性。本文方法目前只针对大型岩体点云,在包含其他特性的点云上的适用性未做深入讨论,这也是后续工作的重点。
| [1] |
Besl P J, McKay N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256. Doi:10.1109/34.121791 |
| [2] |
王飞鹏, 肖俊, 王颖, 等. 一种基于高斯曲率的ICP改进算法[J]. 中国科学院大学学报, 2019, 36(5): 702-708. Doi:10.7523/j.issn.2095-6134.2019.05.016 |
| [3] |
Aiger D, Mitra N J, Cohen-Or D. 4-points congruent sets for robust pairwise surface registration[J]. ACM Transactions on Graphics, 2008, 27(3): 1-10. Doi:10.1145/1360612.1360684 |
| [4] |
Yang B S, Zang Y F. Automated registration of dense terrestrial laser-scanning point clouds using curves[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 95: 109-121. Doi:10.1016/j.isprsjprs.2014.05.012 |
| [5] |
Xian Y R, Xiao J, Wang Y. A fast registration algorithm of rock point cloud based on spherical projection and feature extraction[J]. Frontiers of Computer Science, 2019, 13(1): 170-182. Doi:10.1007/s11704-016-6191-1 |
| [6] |
Wang F P, Xiao J, Wang Y. Efficient rock-mass point cloud registration using n-point complete graphs[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 9332-9343. Doi:10.1109/TGRS.2019.2926201 |
| [7] |
Hu L, Xiao J, Wang Y. An automatic 3D registration method for rock mass point clouds based on plane detection and polygon matching[J]. The Visual Computer, 2020, 36(4): 669-681. Doi:10.1007/s00371-019-01648-z |
| [8] |
Biber P, Straßer W. The normal distributions transform: a new approach to laser scan matching[C]//Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453). October 27-31, 2003, Las Vegas, NV, USA. IEEE, 2003: 2743-2748. DOI: 10.1109/IROS.2003.1249285.
|
| [9] |
Vongkulbhisal J, de La Torre F, Costeira J P. Discriminative optimization: theory and applications to point cloud registration[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). July 21-26, 2017, Honolulu, HI, USA. IEEE, 2017: 3975-3983. DOI: 10.1109/CVPR.2017.423.
|
| [10] |
Elbaz G, Avraham T, Fischer A. 3D point cloud registration for localization using a deep neural network auto-encoder[C]//2017 IEEE Conference on Computer Vision and Pattern Recongition(CVPR). July 21-26, 2017, Honolulu, HI, USA. IEEE, 2017: 2472-2481. DOI: 10.1109/CVPR.2017.265.
|
| [11] |
Lu W X, Wan G W, Zhou Y, et al. DeepVCP: an end-to-end deep neural network for point cloud registration[C]//2019 IEEE/CVF International Conference on Computer Vision (ICCV). October 27-November 2, 2019, Seoul, Korea (South). IEEE, 2019: 12-21. DOI: 10.1109/ICCV.2019.00010.
|
| [12] |
舒程珣, 何云涛, 孙庆科. 基于卷积神经网络的点云配准方法[J]. 激光与光电子学进展, 2017, 54(3): 129-137. Doi:10.3788/LOP54.031001 |
| [13] |
刘鸣, 舒勤, 杨赟秀, 等. 基于独立成分分析的三维点云配准算法[J]. 激光与光电子学进展, 2019, 56(1): 181-189. Doi:10.3788/LOP56.011203 |
| [14] |
Zhang X P, Li H J, Cheng Z L, et al. Robust curvature estimation and geometry analysis of 3D point cloud surfaces[J]. Journal of Information & Computational Science, 2009, 6(5): 1983-1990. |
| [15] |
Holz D, Ichim A E, Tombari F, et al. Registration with the Point Cloud Library: a modular framework for aligning in 3-D[J]. IEEE Robotics & Automation Magazine, 2015, 22(4): 110-124. Doi:10.1109/MRA.2015.2432331 |
| [16] |
Lato M, Kemeny J, Harrap R M, et al. Rock bench: establishing a common repository and standards for assessing rockmass characteristics using LiDAR and photogrammetry[J]. Computers & Geosciences, 2013, 50: 106-114. Doi:10.1016/j.cageo.2012.06.014 |
 2022, Vol. 39
2022, Vol. 39 


