2. 中国科学院上海微系统与信息技术研究所, 上海 200050;
3. 中国科学院大学, 北京 100049
2. Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Science, Shanghai 200050, China;
3. University of Chinese Academy of Science, Beijing 100049, China
移动智能终端的普及与5G、物联网等技术的井喷式发展,让移动网络数据的发送与接收达到了一个前所未有的数量级。仅2014年,全球的移动数据流量总量是2000年整个国际互联网数据总量的30倍[1]。缓存技术能够有效降低网络高峰期数据传输时延,一直以来都是国内外计算机、通信等信息科学领域的研究人员所关注的重要热点,传统缓存方案直接将用户所需要的部分文件存储在本地,当用户向所连接的服务器发出该文件的请求后,由服务器将未存储的另一部分发送到用户,从而满足用户需求。该方案对用户本地的存储空间要求较高,且当多个用户请求不同的文件时,服务器需进行多次发送,传输效率较低。2014年,Maddah-Ali和Niesen[2]针对服务器与多个用户无噪相连的系统模型,提出中心化的编码缓存方案。该方案将传统缓存和编码技术相结合,合理设计缓存问题中的2个阶段:Placement和Delivery,使得服务器发送的信号能同时满足多个用户的请求,从而获得传统缓存方案所不具有的多播增益,有效降低总的传输时延。
目前关于编码缓存的研究已经拓展到多个方向和应用场景。Maddah-Ali和Niesen[3]提出了支持用户数量变化和网络环境切换的去中心化缓存算法。去中心化缓存算法以牺牲少量性能为代价,具有更好的灵活性。在此基础上,国内外许多研究者也开始研究更实际更复杂的系统模型,为编码缓存方案的应用,做出了许多突破性的工作。例如,Karamchandani等[4]考虑服务器与用户之间存在中继辅助连接的多层模型。其中服务器与中继层为第1层网络,中继与所连接的用户为第2层网络。针对该模型,他们提出基于单层网络的多级编码缓存算法,并得到了最优传输时延上下界。更多的关于编码缓存的研究还包括:用户对文件的需求服从非均匀分布的编码缓存问题[5]; 多个服务器向用户提供服务的编码缓存问题[6]; 将编码缓存与分布式计算结合,在通信负载、节点计算量和缓存大小之间寻求一个折衷关系[7]; 以PDA(placement delivery array)的特殊结构来描述编码缓存过程中的2个阶段,同时减小文件划分数量级[8]; 将图论中的超图和二分图用于研究编码缓存[9-10]; 保持文件完整性同时降低传输时延的编码缓存技术[11]; 将编码缓存技术应用到信息安全与私人信息检索领域[12-14]等。
本文针对包含服务器、中继和用户的多层级联网络模型,提出去中心化和中心化的编码缓存方案,并从理论上推导出这2种方案的传输时延上界。该方案利用中继的缓存资源,实现了服务器与中继的并行传输,并通过合理设计Placement和Delivery阶段,使得服务器和中继能够根据自身和用户存储的文件内容,高效地选择发送时机和发送内容。通过数学推导和仿真结果表明,本文所提出的2种缓存方案均严格优于之前针对分层网络所提出的缓存方案,能够明显地降低系统的通信延迟。
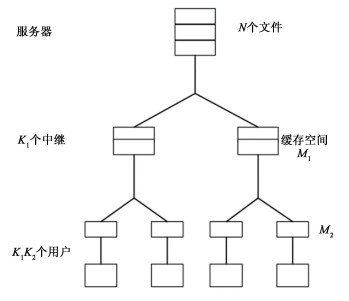
1 分层网络缓存模型如图 1所示,分层缓存网络包含一个存储了N个文件的服务器,每个文件的大小均为F比特,该服务器通过无噪的光比信道连接K1个中继节点,每个中继拥有的缓存空间大小为M1F比特; 同样地,每个中继也以同样的方式连接K2个用户,每个用户也拥有M2F比特的缓存空间,参数M1, M2即为中继和用户的标准化缓存大小。用W1, W2, …, WN表示存储在服务器中的N个文件,定义uji表示与第i个中继连接的第j个用户,其中i∈[K1], j∈[K2],Ui={u1i, …, uK2i}表示中继i所连接的用户集合,U=U1∪…∪UK1表示所有用户的集合。为便于表述,本文使用中括号代表集合符号,此处[K1]表示集合{1, …, K1},[K2]表示集合{1, …, K2}。定义R为衡量系统性能的标准化传输时延,即总的需要发送的文件比特数与F的比值。
|
Download:
|
| 图 1 分层网络编码缓存模型 Fig. 1 Hierarchical coded caching system model | |
在Placement阶段,所有的中继和用户可以预先存储N个文件的部分内容,用以填充其本地缓存空间,这个阶段通常发生在网络流量较低的时段。
Placement阶段完成后,用户uji向服务器提出自身的访问请求dji∈{1, 2, …, N}。本文考虑最差场景下的性能,即所有用户所请求的文件均不相同(对于非最差场景,传输延迟会降低)。当中继和服务器接收到用户的访问请求后,Delivery阶段开始工作。服务器根据用户的请求,将存储的文件进行编码后广播给中继。同时,每个中继根据自身存储以及从服务器接受的内容进行编码,然后将编码后数据广播给连接的用户。用户接收到来自中继的数据后,结合本地存储内容解出自身所需要的部分文件,即可恢复出所请求的整个文件。
本文研究的重点和难点在于,如何在Placement阶段合理地对文件进行分块和存储,以及服务器在知道用户的所有请求之后,如何在Delivery阶段对用户需要的内容进行编码和发送,使得用户在完美解出所需要内容的同时,尽可能降低系统的传输时延。
2 中心化编码缓存方案对于图 1中给出的网络,引入辅助参数t1, t2,令t1=K1M1/N, t2=K2M2/N,计算组合数L=Ct1K1·Ct2K2,中心化分层网络编码缓存即在Placement阶段将所有文件等分成L份子文件。每一个中继和用户都存储了关于所有文件的部分信息,文件Wn通过引入上下标的表示形式说明该子文件存储在中继和用户中的位置,可表示为
| $ \begin{gathered} W_{n} = \left(W_{n, T}^{Q}: Q \subset\left[K_{1}\right], T \subset\left[K_{2}\right],\right. \\ \left.|Q| = t_{1},|T| = t_{2}\right) . \end{gathered} $ |
其中: 上标Q表示子文件Wn, TQ存储在各个中继中的位置索引,即中继i存储了任意满足i∈Q的子文件; 下标T表示子文件Wn, TQ存储在用户中的位置索引。
根据Placement阶段的缓存情况,每个用户需要的子文件可以分为2类:
第1类子文件存储在用户所连接的中继中,表示为
| $ W_{d_{j}^{i}, S \backslash\{j\}}^{Q}, $ |
需满足条件Q[K1], |Q|=t1, S[K2], |S|=t2, i∉Q。
第2类子文件存储在不与该用户连接的中继中,表示为
| $ W_{d_{j}^{i}, S \backslash\{j\}}^{Q}. $ |
需满足条件Q[K1], |Q|=t1, S[K2], |S|=t2, i∈Q。
第1类子文件可以由该用户所连接的中继编码后直接进行发送,且所有中继可以同时工作,即对于所有的用户子集S[K2], |S|=t2+1以及任意j∈[K2],中继i发送编码信息
| $ \oplus_{j \in S} W_{d_{j}^{i}, S \backslash\{j\}}^{R} $ | (1) |
到所连接的用户,其中⊕代表异或操作。
由于不同的中继和所连接的用户之间没有有效通信,第2类子文件由服务器编码后发送到中继,对于任意的R[K1], |R|=t1+1, S[K2], |S|=t2+1,服务器发送编码子文件
| $ \oplus_{i \in R}\left(\oplus_{j \in S} W_{d_{j}^{i}, S \backslash\{j\}}^{R \backslash\{i\}}\right) $ | (2) |
到所有的中继,再由中继根据自身存储文件解出所连接用户需要的部分,分别发送给对应的用户。由于中继并不需要等服务器将第2类子文件发送完毕后再发送给用户,所以发送第1类和第2类子文件的过程可以实现并行发送。
定理1 考虑图 1所示的分层网络,在中心化编码缓存的设定下,其传输时延上界为
| $ \begin{gathered} R_{\mathrm{OUR}_{-} \mathrm{c}} = K_{1} K_{2} \cdot\left(1-\frac{M_{1}}{N}\right) \cdot\left(1-\frac{M_{2}}{N}\right) \cdot\\ \frac{1}{\left(1+\frac{K_{1} M_{1}}{N}\right) \cdot\left(1+\frac{K_{2} M_{2}}{N}\right)}+K_{2} \cdot \frac{M_{1}}{N} \text {. }\\ \left(1-\frac{M_{2}}{N}\right) \cdot \frac{1}{1+\frac{K_{2} M_{2}}{N}} . \end{gathered} $ | (3) |
下面以一个例子来说明中心化方案的Placement和Delivery阶段。
例1 考虑K1=2, K2=2, N=4, M1=2, M2=2的多层网络模型。以A, B, C, D分别表示服务器中的4个文件,用户所需要的文件均不相同但可以是任意的。不失一般性,假设4个用户需要文件分别是A, B, C, D。
计算出t1=t2=1, L=4,每个文件会被分成4等份。对文件A进行切分,可得到A11, A12, A21, A22共4个子文件,其他类似。A21表示既存储于第1个中继又存储于第1个中继所连接的第2个用户的子文件。不难看出,参数t1, t2代表的是切分后的子文件上标和下标中元素的个数,因此Ct1K1代表的是切分文件过程中上标可能的数目,Ct2K2代表的是下标可能的数目,二者的乘积即为切分后子文件的数目。同时,该存储设定也可以令缓存内容的大小刚好满足中继和用户的缓存空间。
表 1给出了2个中继连接的4个用户需求和缓存的基本情况,可以看出,用户1和用户3,用户2和用户4所缓存的内容是完全相同的,这是由于它们在不同中继上的相对位置是一样的,即不同中继所连接用户的缓存内容具有对称性。
|
|
表 1 中心化方案用户文件缓存与需求 Table 1 Caching and requesting contents in centralized scheme |
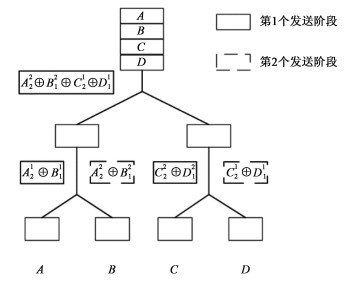
根据2类子文件发送的算法式(1)和式(2),图 2给出中心化方案的发送过程。
|
Download:
|
| 图 2 中心化方案发送过程 Fig. 2 Delivery of centralized scheme | |
首先,在第1个发送阶段,服务器通过共享链路向2个中继发送第1类子文件编码A22⊕B12⊕C21⊕D11; 同时,2个中继分别向所连接用户发送已存储的第2类子文件编码A21⊕B11,C22⊕D12,用户1,2,3,4即可以根据收到的信息进行解码,得到各自需要的第1类子文件A21,B11,C22,D12。在第2个发送阶段,服务器不再需要发送任何内容,2个中继根据前面收到的第2类子文件编码进行解码。中继1得到A22⊕B12,中继2得到C21⊕D11,然后发送给所连接的用户,用户解出需要的第2类子文件,从而所有用户均解出了需要的子文件,完成了文件访问需求。整个过程只需要2次子文件发送,因此ROUR_c=1/2。
3 去中心化编码缓存方案在Placement阶段对文件进行分割及缓存时,中心化方案将文件等分成固定数目的子文件,每个中继或用户存储每个文件的比例是相同的。而去中心化方案从概率统计的角度来考虑文件分割以及存储。假设所有文件独立且满足均匀分布,中继以随机选取的方式对文件进行缓存,那么对于任意一个文件所含的任意一个比特,能够被某一中继缓存的概率是M1/N,反之,不能够被某一中继缓存的概率是1-M1/N。同理,能够被某一用户缓存的概率是M2/N,不能够被某一用户缓存的概率是1-M2/N。根据存储位置的不同,文件Wn可被分为多个子文件,表示为
| $ W_{n} = \left\{W_{n, S}^{Q}, Q \subseteq\left[K_{1}\right], S \subseteq\left[K_{2}\right]\right\}. $ |
其中:上标Q表示子文件Wn, SQ存储在中继中的位置索引,下标S表示其存储在用户中的位置索引。假设文件的大小可以趋向于无穷大,根据大数定律,存储在中继或用户中子文件的大小为
| $ \begin{gathered} \left|W_{n, S}^{Q}\right| \approx\left(\frac{M_{1}}{N}\right)^{|Q|} \cdot\left(1-\frac{M_{1}}{N}\right)^{K_{1}-|Q|} \cdot\left(\frac{M_{2}}{N}\right)^{|S|} \cdot \\ \left(1-\frac{M_{2}}{N}\right)^{K_{1} K_{2}-|S|} F. \end{gathered} $ | (4) |
与中心化方案子文件不同的是,这里表示存储中继集合的Q和表示存储用户集合的S均可以为空集Ø。空集表示该部分子文件并未存储在任何一个中继或用户当中。
在Delivery阶段,对于任意一个中继i所连接的用户,所需要的子文件可以分为以下3类:
第1类被除中继i之外的其他中继所存储的子文件,表示为
| $ W_{d_{j}^{i}, S \backslash\left\{u_{j}^{i}\right\},}^{Q}, S \subset U, Q \subset\left[K_{1}\right], i \notin Q, $ |
第2类没有被任何中继存储的子文件,表示为
| $ W_{d_{j}^{i}, S \backslash\left\{u_{j}^{i}\right\}}^{\varnothing}, S \subset U, $ |
第3类被中继i所存储的子文件,表示为
| $ W_{d_{j}^{i}, S \backslash \{ u_{j}^{i}\}}^{Q}, S \subset U, Q \subseteq\left[K_{1}\right], i \in Q. $ |
因此,整个Delivery阶段发送3类子文件的过程也可以分为以下3步。
第1个发送阶段主要针对第1类子文件。由于中继之间并没有任何直接或间接的通信,因此第1类子文件将由服务器直接进行编码多播发送,对于任意的j∈[K2],服务器向所有的中继发送编码信息
| $ \oplus_{i \in R}\left(\oplus_{u_{j}^{i} \in S} W_{d_{j}^{i}, S_{i} \backslash\left\{u_{j}^{i}\right\} \cup T}^{R \backslash\{i\}}\right). $ | (5) |
考虑到并行发送的网络属性,此阶段中继i在解出需要的子文件之后,直接发送给所连接的用户,以R1表示此阶段的传输时延。
第2个发送阶段主要针对第2类子文件和部分第3类子文件。第2类子文件即上标为Ø且被用户所需要的部分,由服务器编码多播发送到所有中继,遍历所有用户子集S⊆U: |S|=s, s∈[K1K2],服务器发送
| $ \oplus_{u_{j}^{i} \in S} W_{d_{j}^{i}, S \backslash \{u_{j}^{i}\}}^{\varnothing} $ | (6) |
到所有中继,同时中继将接收到的子文件选择性地发送到自己所连接的用户。因为服务器发送的是针对所有用户的第2类子文件,而每个中继只需要发送其连接用户所需要的第2类子文件,所以服务器所发送第2类子文件中有一部分对于某些中继是冗余的信息,此时这些中继可以再将自身缓存的第3类文件发送给用户,即中继i发送
| $ \oplus_{u_{j}^{i} \in S_{i}^{\prime}} W_{d_{j}^{i}, S_{i}^{\prime} \backslash\left\{u_{j}^{i}\right\} \cup T^{\prime}}^{R^{\prime}}. $ | (7) |
也就是本身存储在中继中被下面所连接的用户需要的子文件,其中
| $ R^{\prime} \subseteq\left[K_{1}\right]: i \in R, $ |
| $ S_{i}^{\prime} \subseteq U_{i}:\left|S_{i}\right| = s, s \in\left[K_{2}\right], $ |
| $ T^{\prime} \subseteq U \backslash U_{i}:\left|T^{\prime}\right| = t, t = K_{1} K_{2}-K_{2}, \cdots, 0. $ |
以R2表示此阶段的传输时延。
在第3个发送阶段,中继发送剩余的第3类子文件。如果第3类子文件在第2个发送阶段已全部发送给到用户,那么所有发送过程均已完成,即第3个阶段不存在。因此此阶段存在的前提是,在服务器发送到中继的第2类子文件中,中继不需要的那部分子文件大小小于第3类子文件的大小,以R3表示此阶段的传输时延。
总结来说,表 2给出了去中心化方案中3类子文件的发送过程,第1类子文件由服务器和中继直接进行并行传输,传输时延即为第1类子文件的标准化大小R1; 在第2个发送步骤,服务器向中继发送所有的第2类子文件,中继利用并行传输发送第2类子文件中必要的部分信息以及部分第3类子文件,总的传输时延为R2; 若第3类子文件总的大小小于第2类子文件中冗余信息的大小,则整个发送过程结束,反之,则中继继续发送剩下的第3类子文件。
|
|
表 2 第1、2、3类子文件的发送 Table 2 Delivery of three types of subfiles |
定理2 考虑图 1所示的分层网络,在去中心化编码缓存的设定下,令
| $ r\left(\frac{M}{N}, K\right) = K \cdot\left(1-\frac{M}{N}\right) \cdot \frac{N}{K M}\left(1-\left(1-\frac{M}{N}\right)^{K}\right), $ | (8) |
则整个过程的传输时延上界为
| $ R_{1} = \left[r\left(\frac{M_{1}}{N}, K_{1}\right)-K_{1} \cdot\left(1-\frac{M_{1}}{N}\right)^{K_{1}}\right] \cdot r\left(\frac{M_{2}}{N}, K_{2}\right), $ | (9) |
| $ R_{2} = \left(1-\frac{M_{1}}{N}\right)^{K_{1}} \cdot r\left(\frac{M_{2}}{N}, K_{1} K_{2}\right), $ | (10) |
| $ R_{\mathrm{OUR}\_{\mathrm{d}}} = R_{1}+R_{2}+R_{3}. $ |
| $ \begin{gathered} R_{3} = \max \left(\frac{M_{1}}{N} \cdot r\left(\frac{M_{2}}{N}, K_{2}\right)-\left(1-\frac{M_{1}}{N}\right)^{K_{1}}\cdot\right. \\ \left.\left(1-\frac{M_{2}}{N}\right)^{K_{2}} \cdot r\left(\frac{M_{2}}{N},\left(K_{1}-1\right) K_{2}\right), 0\right). \end{gathered} $ | (11) |
下面以一个例子来说明去中心化方案的Placement和Delivery阶段
例2 考虑N=4, K1=K2=2, M1=M2=2的多层网络模型。以A, B, C, D表示服务器中的4个文件,用户所需要的文件均不相同但可以是任意的。不失一般性,假设4个用户需要的访问文件分别为A, B, C, D。
在Placement阶段,去中心化方案将文件A划分为多个子文件
| $ A = \left\{A_{S}^{\varnothing}, A_{S}^{1}, A_{S}^{2}, A_{S}^{1,2}\right\}. $ |
其中:S⊂{1, 2, 3, 4},所以A被分成了2K1·2K1K2=64个子文件。其余文件B, C, D类似。由式(4)可得,分割之后的子文件大小为
| $ \begin{aligned} \left|W_{n, S}^{Q}\right| \approx &\left(\frac{1}{2}\right)^{|Q|} \cdot\left(\frac{1}{2}\right)^{2-|Q|} \cdot\left(\frac{1}{2}\right)^{|S|} \cdot \\ &\left(\frac{1}{2}\right)^{4-|S|} \cdot F = \frac{1}{64} F . \end{aligned} $ |
在第1个发送阶段,根据第1类子文件的发送算法式(6),服务器向中继发送第1类子文件
| $ A_{\varnothing}^{2} \oplus C_{\varnothing}^{1}, B_{\varnothing}^{2} \oplus D_{\varnothing}^{1}, A_{2}^{2} \oplus B_{1}^{2} \oplus C_{4}^{1} \oplus D_{3}^{1}, $ |
| $ A_{3}^{2} \oplus C_{1}^{1}, A_{4}^{2} \oplus C_{2}^{1}, B_{3}^{2} \oplus D_{1}^{1}, B_{4}^{2} \oplus D_{2}^{1}, $ |
| $ A_{2,3}^{2} \oplus B_{1,3}^{2} \oplus C_{1,4}^{1} \oplus D_{1,3}^{1}, A_{3,4}^{2} \oplus C_{1,2}^{1}, $ |
| $ A_{2,4}^{2} \oplus B_{1,4}^{2} \oplus C_{2,4}^{1} \oplus D_{2,3}^{1}, B_{3,4}^{2} \oplus D_{1,2}^{1}, $ |
| $ A_{2,3,4}^{2} \oplus B_{1,3,4}^{2} \oplus C_{1,2,4}^{1} \oplus D_{1,2,3}^{1} . $ |
中继1可以将上标为2的子文件解出来,中继2也可以将上标为1的子文件解出来,然后直接发送到所连接的用户,用户可以根据存储内容进一步解出所需要的子文件,这个过程的传输时延R1=3/16。
第2个发送阶段,根据第2类子文件的发送算法式(7),服务器向中继继续发送第2类子文件
| $ A_{\varnothing}^{\varnothing}, B_{\varnothing}^{\varnothing}, C_{\varnothing}^{\varnothing}, D_{\varnothing}^{\varnothing}, A_{2}^{\varnothing} \oplus B_{1}^{\varnothing}, A_{3}^{\varnothing} \oplus C_{1}^{\varnothing}, $ |
| $ A_{4}^{\varnothing} \oplus D_{1}^{\varnothing}, C_{2}^{\varnothing} \oplus B_{3}^{\varnothing}, D_{2}^{\varnothing} \oplus B_{4}^{\varnothing}, C_{4}^{\varnothing} \oplus D_{3}^{\varnothing}, $ |
| $ A_{2,3}^{\varnothing} \oplus B_{1,3}^{\varnothing} \oplus C_{1,2}^{\varnothing}, A_{2,4}^{\varnothing} \oplus B_{1,4}^{\varnothing} \oplus D_{1,2}^{\varnothing}, $ |
| $ A_{3,4}^{\varnothing} \oplus C_{1,4}^{\varnothing} \oplus D_{1,3}^{\varnothing}, B_{3,4}^{\varnothing} \oplus C_{2,4}^{\varnothing} \oplus D_{2,3}^{\varnothing}, $ |
| $ A_{2,3,4}^{\varnothing} \oplus B_{1,3,4}^{\varnothing} \oplus C_{1,2,4}^{\varnothing} \oplus D_{1,2,3}^{\varnothing} . $ |
对于中继1而言,上述子文件中不需要的部分为CØØ, DØØ, C4Ø⊕D3Ø。同理,对于中继2而言,不需要的部分为AØØ, BØØ, A2Ø⊕B1Ø,此部分空缺由第3类子文件补上,这个发送过程的传输时延为R2=15/64。
第3个发送阶段,即服务器需要发送的内容已发送完毕,由中继将自身存储内容进行编码发送,根据第3类子文件的发送算法式(8),中继1发送的第3类子文件为
| $ A_{\varnothing}^{Q_{1}}, B_{\varnothing}^{Q_{1}}, A_{2}^{Q_{1}} \oplus B_{1}^{Q_{1}}, A_{3}^{Q_{1}}, A_{4}^{Q_{1}}, $ |
| $ B_{3}^{Q_{1}}, B_{4}^{Q_{1}}, A_{2,3}^{Q_{1}} \oplus B_{1,3}^{Q_{1}}, A_{2,4}^{Q_{1}} \oplus B_{1,4}^{Q_{1}}, $ |
| $ A_{3,4}^{Q_{1}}, B_{3,4}^{Q_{1}}, A_{2,3,4}^{Q_{1}} \oplus B_{1,3,4}^{Q_{1}} . $ |
其中:Q1{1, 2}并且包含元素1,此处为{1}或{1, 2}。中继2发送的第3类子文件为
| $ C_{\varnothing}^{Q_{2}}, D_{\varnothing}^{Q_{2}}, C_{4}^{Q_{2}} \oplus D_{3}^{Q_{2}}, C_{1}^{Q_{2}}, D_{2}^{Q_{2}}, $ |
| $ C_{\varnothing}^{Q_{2}}, D_{\varnothing}^{Q_{2}}, C_{4}^{Q_{2}} \oplus D_{3}^{Q_{2}}, C_{4}^{Q_{2}} \oplus D_{3}^{Q_{2}}, $ |
| $ C_{1,2}^{Q_{2}}, D_{1,2}^{Q_{2}}, C_{1,2,4}^{Q_{2}} \oplus D_{1,2,3}^{Q_{2}} . $ |
其中:Q⊂2{1, 2}并且包含元素2,此处为{2}或{1, 2},取部分文件补上第2阶段的空缺后,这个过程的传输时延为R3=21/64。
由此,可计算出总的传输时延ROUR_d=3/4。
4 性能分析本节将通过理论推导与仿真结果,从中心化和去中心化的角度,对本文所提出的2种方案与文献[4]的方案进行分析与比较。
在文献[4]的方案中服务器和中继连接的一层被看作第1层网络,中继和用户连接的一层被看作第2层网络。第1层网络使用单层的中心化或去中心化编码缓存算法,使得中继能够重建出所连接用户需要的文件,之后第2层网络将每个中继看作服务器,再次使用单层的编码缓存算法,通过发送编码多播子文件,满足其连接用户的文件访问请求。其中心化和去中心化方案的传输时延分别为
| $ \begin{gathered} R_{\mathrm{AN}\_{\mathrm{c}}} = K_{1} K_{2} \cdot\left(1-\frac{M_{1}}{N}\right) \cdot \frac{1}{1+\frac{K_{1} M_{1}}{N}}+ \\ K_{2} \cdot\left(1-\frac{M_{2}}{N}\right) \cdot \frac{1}{1+\frac{K_{2} M_{2}}{N}}, \end{gathered} $ | (12) |
| $ R_{\mathrm{AN}\_\mathrm{d}} = K_{2} \cdot r\left(\frac{M_{1}}{N}, K_{1}\right)+r\left(\frac{M_{2}}{N}, K_{2}\right). $ | (13) |
首先比较本文和文献[4]的中心化编码缓存方案。从式(3)和式(12)可以看出,ROUR_c加号左右两边的2项,均是在RAN_c 2项的基础上乘上小于1的因子,因此ROUR_c≤RAN_c,从理论上证明本文所提出的中心化方案能够获得更低的传输延迟。在例1中,若使用文献[4]的方案,将参数带入计算可得RAN_c=3/2,而本文提出的方案ROUR_c=1/2,与代入参数后式(3)的结果相同,性能提升了3倍,效果十分显著。
比较本文和文献[4]的去中心化编码缓存方案。由于r(M2/N, K2)≤K2,且
| $ \begin{gathered} R_{1}+R_{2} \leqslant K_{2} r\left(\frac{M_{1}}{N}, K_{1}\right)+\left(1-\frac{M_{1}}{N}\right)^{K_{1}}\cdot\\ \left(r\left(\frac{M_{2}}{N}, K_{1} K_{2}\right)-K_{1} r\left(\frac{M_{2}}{N}, K_{2}\right)\right) \leqslant K_{2} r\left(\frac{M_{1}}{N}, K_{1}\right), \end{gathered} $ |
| $ R_{3} \leqslant \frac{M_{1}}{N} \cdot r\left(\frac{M_{2}}{N}, K_{2}\right) \leqslant r\left(\frac{M_{2}}{N}, K_{2}\right), $ |
因此
| $ R_{1}+R_{2}+R_{3} \leqslant K_{2} r\left(\frac{M_{1}}{N}, K_{1}\right)+r\left(\frac{M_{2}}{N}, K_{2}\right) = R_{\mathrm{AN}\_d}. $ |
即ROUR_d=R1+R2+R3≤RAN_d,在理论上证明了本文所提出的去中心化方案仍然严格优于文献[4]的方案。在例2中,总的传输时延ROUR_d=3/4,而将参数代入式(13),计算出文献[4]去中心化方案的传输时延为RAN_d=9/4,显然,本文所提出的方案传输时延明显降低。
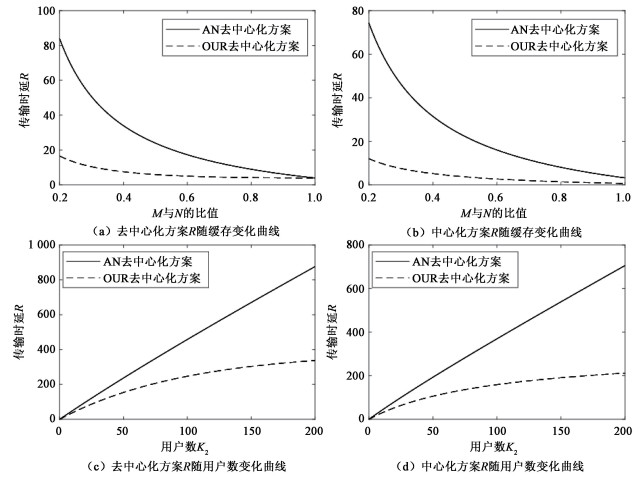
图 3(a)和(b)设定K1=40, K2=20, M2/N=0.2,以M1/N作为横坐标,传输时延R作为纵坐标。可以明显看出:中心化方案和去中心化方案的传输时延R均随着M1/N的增大而减小。这是当M1/N的增大时,中继缓存能力提升,因此服务器所需要发送的内容会减少,传输时延也随之降低; 在中心化和去中心化的设定上,本文所提出的2种方案与文献[4]的方案相比,均体现出非常明显的性能优势,特别是在M1/N取值较小的时候; 同样的参数设置,由于中心化的存储要求更严格,去中心化对文件进行分割存储的自由度更高,所以中心化方案的传输时延要略好于去中心化方案。
|
Download:
|
| 图 3 中心化和去中心化方案性能对比 Fig. 3 Performance comparison of centralized and decentralized scheme | |
图 3(c)和(d)设定M1/N=0.2, M2/N=0.01, K1=20,以每个中继连接的用户数量K2作为横坐标,整个系统的传输时延R作为纵坐标。可以看出:随着用户数目K2的增加,整个网络的负载增大,传输时延也增大; 本文提出的中心化和去中心化方案均明显优于文献[4]的方案; 在文献[4]的2种方案中,传输时延与用户数目基本都保持线性增长关系,而本文提出来的2种方案,传输时延随用户数目的增长速率相对来说较为缓慢,远远低于线性增长,意味着本文提出的方案具有更强的鲁棒性和可延展性。
5 总结本文针对包含服务器、中继和用户的分层网络模型,提出了中心化和去中心化的2种编码缓存方案。2种方案充分利用中继的缓存资源,合理设计Placement和Delivery阶段,在满足用户文件请求的同时,实现了数据的高效传输。通过理论推导和仿真验证,与文献[4]的编码缓存方案相比,本文提出的方案显著地降低系统的传输延迟,同时具有更强的鲁棒性以及可延展性。
| [1] |
Cisco. Cisco visual networking index: global mobile data traffic forecast update, 2015-2020 white paper[R/OL]. 2016, Document ID 958959758. (2017-05-26) [2020-04-02]. http://www.cisco.com/c/en/us/solutions/service-provide/visual-networking-index-vni/index.html.
|
| [2] |
Maddah-Ali M A, Niesen U. Fundamental limits of caching[J]. IEEE Transactions on Information Theory, 2014, 60(5): 2856-2867. Doi:10.1109/TIT.2014.2306938 |
| [3] |
Maddah-Ali M A, Niesen U. Decentralized coded caching attains order-optimal memory-rate tradeoff[J]. IEEE/ACM Transactions on Networking, 2015, 23(4): 1029-1040. Doi:10.1109/TNET.2014.2317316 |
| [4] |
Karamchandani N, Niesen U, Maddah-Ali M A, et al. Hierarchical coded caching[J]. IEEE Transactions on Information Theory, 2016, 62(6): 3212-3229. Doi:10.1109/TIT.2016.2557804 |
| [5] |
Niesen U, Maddah-Ali M A. Coded caching with nonuniform demands[J]. IEEE Transactions on Information Theory, 2017, 63(2): 1146-1158. Doi:10.1109/TIT.2016.2639522 |
| [6] |
Shariatpanahi S P, Motahari S A, Khalaj B H. Multi-server coded caching[J]. IEEE Transactions on Information Theory, 2016, 62(12): 7253-7271. Doi:10.1109/TIT.2016.2614722 |
| [7] |
Li S Z, Maddah-Ali M A, Yu Q, et al. A fundamental tradeoff between computation and communication in distributed computing[J]. IEEE Transactions on Information Theory, 2018, 64(1): 109-128. Doi:10.1109/TIT.2017.2756959 |
| [8] |
Yan Q F, Cheng M Q, Tang X H, et al. On the placement delivery array design for centralized coded caching scheme[J]. IEEE Transactions on Information Theory, 2017, 63(9): 5821-5833. Doi:10.1109/TIT.2017.2725272 |
| [9] |
Shangguan C, Zhang Y W, Ge G N. Centralized coded caching schemes: a hypergraph theoretical approach[J]. IEEE Transactions on Information Theory, 2018, 64(8): 5755-5766. Doi:10.1109/TIT.2018.2847679 |
| [10] |
Yan Q F, Tang X H, Chen Q C, et al. Placement delivery array design through strong edge coloring of bipartite graphs[J]. IEEE Communications Letters, 2018, 22(2): 236-239. Doi:10.1109/LCOMM.2017.2765629 |
| [11] |
Saberali S A, Lampe L, Blake I F. Decentralized coded caching without file splitting[J]. IEEE Transactions on Wireless Communications, 2019, 18(2): 1289-1303. Doi:10.1109/TWC.2019.2891618 |
| [12] |
Ravindrakumar V, Panda P, Karamchandani N, et al. Private coded caching[J]. IEEE Transactions on Information Forensics and Security, 2018, 13(3): 685-694. Doi:10.1109/TIFS.2017.2765503 |
| [13] |
Kamel S, Sarkiss M, Wigger M, et al. Secrecy capacitymemory tradeoff of erasure broadcast channels[J]. IEEE Transactions on Information Theory, 2019, 65(8): 5094-5124. Doi:10.1109/TIT.2019.2902578 |
| [14] |
Tandon R. The capacity of cache aided private information retrieval[C]//2017 55th Annual Allerton Conference on Communication, Control, and Computing. October 3-6, 2017, Monticello, IL, USA. IEEE, 2017: 1078-1082. DOI: 10.1109/ALLERTON.2017.8262857.
|
 2022, Vol. 39
2022, Vol. 39 


