非正交多址接入(non-orthogonal multiple access, NOMA)技术可以显著提高频谱效率，并在5G的系统吞吐量和用户公平性之间取得良好的平衡。换句话说，NOMA可以及时为具有不同信道条件的用户提供服务，这为满足超低等待时间和超高连接性的5G要求提供了可能性^[1]。最近，许多研究学者和专家提出了各种多址接入技术方案^[2]，包括功率域非多址接入技术和稀疏代码多址接入技术^[3]。Benjebbovu等^[1]通过评估使用非正交多址接入技术在蜂窝网络中的性能指标，表明不同的用户配对方案对非正交多址接入的网络性能影响。Ding等^[4]分析基于距离的用户配对的覆盖率，通过将用户与更独特的信道条件进行配对，非正交多址接入技术与正交多址接入技术(orthogonal multiple access, OMA)相比，网络的性能增益得到显著提升。此外，针对协同传输^[5], 多输入多输出(multiple input multiple output, MIMO)传输网络^[6]，不饱和流量网络^[7]以及上行链路传输网络^[8]都分析了NOMA的性能。

毫米波通信网络随着5G的发展，作为一种有前途的利用新的频谱资源技术，成为重要的手段之一^[9]。毫米波网络具有2个关键特征，即天线定向性和对阻塞效应的敏感性^[9]问题。本文的研究主题无线网络的最新研究热点领域，吸引了大量相关学者的关注。Bai和Heath^[10]分析毫米波网络中正交多址接入传输技术用户的覆盖率，其中用天线方向图的近似扇区来分析波束成形方向图，而Yu等^[11]认为正弦模型更接近真实扇形天线方向图模型，并作了深入研究。在毫米波网络中应用NOMA可以进一步提高网络性能^[12-15]。Sun等^[13]分析集群毫米波网络中NOMA的性能，分别采用随机的用户配对策略。Yi等^[14]采用基于距离的用户配对策略。但是，这些研究都没有在用户配对策略的设计中考虑天线定向传输特点。因此所有配对的用户可能不会充分利用天线阵列带来的高增益。Zhou等^[15]提出一种基于角度的用户配对策略，用以提高配对用户被基站主波束覆盖的可能性。但是，这些研究工作基本都采用了简化的扇形天线方向图模型，另外重要的距离信息并未考虑。

本课题考虑毫米波网络的下行链路传输场景，同时考虑到由均匀线性阵列生成的波束成形模式，以视距球模型来模拟毫米波网络中的链路阻塞以及用户在空间中随机分布。

为了促进毫米波网络中的NOMA传输，本文提出一种基于角度和距离的联合用户配对策略。位于最靠近基站的用户与位于距基站一定距离并且具有最小相对空间角度差的另一用户配对。为解决定向波束形成和最小空间角度差的随机性，基站选择性地启用NOMA或OMA方案。本文分析了距离和最小空间角度差的分布，并得出用户的遍历速率。分析结果将通过MATLAB平台仿真进行验证。仿真实验表明，本文所提出的方案比基于角度的NOMA、基于距离的NOMA以及传统NOMA方案和OMA方案具有更好的性能，并且存在距离阈值的最优值，该最优值使遍历总速率最大化，证实了角度和距离信息对用户配对的重要性。

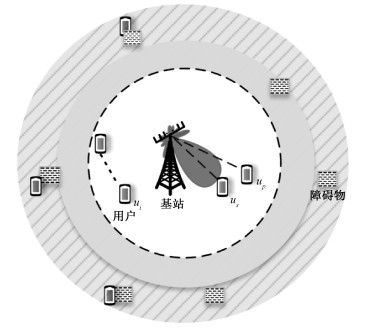
1 系统模型

如图 1所示，考虑一个毫米波网络的下行链路使用非正交多址接入传输场景。配备N根天线的基站位于圆形网络覆盖区域的中央，具有单根天线用户形成一个均匀的泊松点过程，记为Ф={x₁, x₂, …}，其中x_i是用户u_i的空间位置，用户密度表示为λ。在毫米波频率波段下进行户外传输时，每个通信链路都极易受到阻塞障碍物的干扰。因此在研究问题建模时，可以分为视距或非视距链路。本文采用视距球模型，长度r为视距的链路的概率为p_L=1(r≤R_L)，其中1(·)表示指示函数，R_L表示视距链路的最大长度。这样的建模在很多文献中得到了证明，可以忽略不同链路之间的阻塞效应的相关性，因为链路之间的相关性只会在性能分析的准确性上造成较小的损失误差影响。

通常在毫米波频率下的室外传输，非视距的链路很可能会因严重的路径损耗而中断，并始终处于中断状态^[16]。因此，本文将讨论的重点放在路径损耗和准静态信道衰落的视距链路上。l(r)=C_Lr^-β_L表示长度为r的视距链路的路径损耗，其中C_L和β_L分别表示常数参数和路径损耗指数。由于散射有限，假定每个链路都是独立的Nakagami-m衰落。基站和用户u_i之间的信道增益，表示为|h_i²|，它是归一化的伽马随机变量，即Γ(M_L, 1/M_L)，其中M_L为正整数。

为了准确表示定向传输，采用了实际天线阵列模型。对应于空间偏离角$ \vartheta_{i}$的阵列响应向量为

$ \boldsymbol{a}\left(\vartheta_{i}\right) = \frac{1}{\sqrt{N}}\left(1, \cdots, \mathrm{e}^{\mathrm{j} 2 {\rm{ \mathsf{ π} }} k \rho \vartheta_{i}}, \cdots, \mathrm{e}^{\mathrm{j} 2 {\rm{ \mathsf{ π} }}(N-1) \rho \vartheta_{i}}\right)^{\mathrm{T}}. $

(1)

其中：(·)^T表示转置，$\vartheta_{i}=\cos \phi_{i}$是基站与用户u_i之间信道的空间偏离角，$\phi_{i}$是物理偏离角，ρ是天线间距与波长之比，k∈{0, 1, …，N-1}是天线序号索引。为避免出现栅瓣，通常将天线密集放置。空间偏离角$\vartheta_{i}$可以近似为[-1, 1]上均匀分布的随机变量。为降低由于数字信号处理而导致的硬件成本和功耗，本文考虑使用模拟波束成形。模拟波束成形矢量由$\boldsymbol{w}=\boldsymbol{a}(\theta)$给出，其中θ表示基站与目标用户之间信道的空间偏离角，并且均匀分布在[-1, 1]上。因此，用户u_i获得的天线阵列增益，即$\left|\boldsymbol{a}^{\mathrm{H}}\left(\boldsymbol{\vartheta}_{i}\right) \boldsymbol{w}\right|^{2}$，为

$ G\left(\vartheta_{i}-\theta\right) = \frac{\sin ^{2}\left({\rm{ \mathsf{ π} }} \rho N\left(\vartheta_{i}-\theta\right)\right)}{N^{2} \sin ^{2}\left({\rm{ \mathsf{ π} }} \rho\left(\vartheta_{i}-\theta\right)\right)} = \frac{\sin ^{2}\left({\rm{ \mathsf{ π} }} \rho N \varphi_{i}\right)}{N^{2} \sin ^{2}\left({\rm{ \mathsf{ π} }} \rho \varphi_{i}\right)}. $

(2)

为了符号上的方便，其中$\vartheta_{i}-\theta$被替换为φ_i。由于$\vartheta_{i}$和θ是均匀分布，那么φ_i也均匀分布在[-1, 1]上。通过波束跟踪技术，基站可以调整其波束方向以使其自身与目标用户之间的信道向量对齐。

2 新型的非正交多址接入传输策略 2.1 匹配用户的选择准则

为了准确表示本文考虑两个用户NOMA传输的场景。为增强网络性能，选择离基站最近的用户并将其表示为u_s。为解决毫米波网络中的定向传输问题，提出一种基于角度和距离联合的用户配对策略

$ x_{p} = \arg \min \limits_{x_{i} \in \Phi\left(R_{T}\right) \backslash\left\{x_{s}\right\}} \varphi_{i s}. $

(3)

选择配对的用户表示为u_p，其中x_p表示用户u_p的位置，R_T是距离阈值。$\varPhi\left(R_{T}\right)=\left\{x_{i} \mid r_{i} <\right. \left.R_{T}\right\}$，其中r_i是基站与用户u_i之间的距离，并且φ_is=|φ_i -φ_s|是用户u_i和u_s之间空间角度差的绝对值。

每个用户的位置变化都比瞬时信道增益慢得多，因此可以假设基站中已知用户的位置信息。传统的基于距离的用户配对策略仅利用了适合于6 GHz以下网络的距离信息，却忽略了毫米波网络的关键特征(即定向传输)。如果不考虑角度信息，则2个NOMA用户同时被基站的定向波束覆盖的可能性会很低，因此无法充分利用天线阵列增益。另一方面，常规的基于角度的用户配对策略充分利用了天线阵列增益，但是没有考虑距离信息，可能导致毫米波网络中的较大传播损耗。所提出的用户配对策略充分利用了基于距离和基于角度的用户配对策略的优势，即充分利用毫米波网络中NOMA优势。

2.2 新型传输策略的分析

由于空间角度差(即φ_ps)的随机性，本文考虑了一种有选择的传输方案，可以将其分类为以下3种情况。情况1：如果空间角度差φ_ps < ε，其中ε是假设定好的角度阈值，则基站会同时为用户u_s和u_p使用NOMA服务。情况2：如果空间角度差φ_ps>ε，则基站无法使用NOMA同时为2个用户提供较高的传输增益，因此，基站使用OMA为2个用户提供服务。情况3：如果不存在用户u_p，则基站仅使用OMA为用户服务。用户u_s和u_p的功率分配系数分别为α_s和α_p，α_s+α_p=1且α_p>α_s。

NOMA传输    在情况1中，首先解码用户u_p的信号。基站调整其朝向用户u_s的波束方向。因此，基站和用户u_s之间的阵列增益为NG(0)，由于G(0)=1，因此等于N。传输给用户u_p的信号并由用户u_s解码的信号与干扰加噪声比(SINR)为

$ \varGamma_{p \rightarrow s} = \frac{\alpha_{p} N P_{B}\left|h_{s}\right|{ }^{2} l\left(r_{s}\right)}{\alpha_{s} N P_{B}\left|h_{s}\right|^{2} l\left(r_{s}\right)+\sigma^{2}}, $

(4)

其中：P_B表示基站的发射功率，σ²表示加性高斯白噪声的方差。如果用户u_s无法解码传输用户u_p的信号，则它无法解码自己的信号。否则，用户u_s解码自己的信号，其信噪比(SNR)为

$ \varGamma_{s} = \alpha_{s} N P_{B}\left|h_{s}\right|^{2} l\left(r_{s}\right) / \sigma^{2}, $

(5)

另一方面，用户u_p将把用户u_s的信号视为噪声并解码自己的信号，SINR为

$ \varGamma_{p | s} = \frac{\alpha_{p} N P_{B}\left|h_{p}\right|^{2} l\left(r_{p}\right) G\left(\varphi_{p s}\right)}{\alpha_{s} N P_{B}\left|h_{p}\right|^{2} l\left(r_{p}\right) G\left(\varphi_{p s}\right)+\sigma^{2}}, $

(6)

其中，φ_ps=|φ_p-φ_s|和G(φ_ps)是当用户u_s与u_p之间的空间角度差为φ_ps时，基站与用户u_p间的阵列增益。

OMA传输    发生情况2或情况3时，将启用OMA传输方案。基站调整其波束方向以使其自身与用户u_s之间的信道矢量对准。因此，在用户u_i，其中i∈{s, p}处观察到的SNR为

$ \varGamma_{i}^{\mathrm{OMA}} = N P_{B}\left|h_{i}\right|^{2} l\left(r_{i}\right) / \sigma^{2}. $

(7)

请注意，在情况3中，没有找到条件满足的匹配用户u_p，此时基站仅服务用户u_s。

3 用户遍历总速率分析

在本节中，先推导了涉及SINR的随机变量的概率密度函数，再通过随机几何数学用以分析用户的遍历总速率。假设有K≥1个用户在集合Φ(R_T)中，则基站与用户u_s之间距离r_s的条件概率密度函数为

$ f_{r_{s}}(r) = 2 K r R_{T}^{-2}\left(1-r^{2} / R_{T}^{2}\right)^{K-1}, 0<r<R_{T}. $

(8)

基于提出的用户配对策略，用户u_p必须与用户u_s不是同一个，并且其到基站的距离应大于其到用户u_s的距离，即r_p>r_s。如果存在配对的用户，则基站与用户之间距离r_p的条件概率密度函数为

$ f_{r_{p} \mid r_{s}}(r) = \left\{\begin{array}{cc} 2 r\left(R_{T}^{2}-r_{s}^{2}\right)^{-1}, & r_{s}<r<R_{T} \\ 0, & r \leqslant r_{s} \end{array},\right. $

(9)

假设在集合Φ(R_T)中至少有1个以上用户(即K≥1)，并且根据给出的用户配对策略，则用户u_s与u_p之间的空间角度差φ_ps随机变量的概率密度函数：

$ f_{\varphi_{p s}}(\varphi) = (K-1)(1-\varphi / 2)^{2 K-3}, 0 \leqslant \varphi \leqslant 2. $

(10)

距离r_s的概率密度函数和空间角度差φ_ps取决于限制区域集合Φ(R_T)中的用户的数量，这又取决于用户密度λ和半径。对于NOMA传输，用户u_s和u_p的接收阈值分别为τ_s=2^ν_s-1和τ_p=2^ν_p-1，其中ν_s和ν_p表示相应的目标数据速率。当用户u_s靠近基站时，如果成功执行SIC并且其自身信号的SNR大于接收阈值，则它可以解码其自身的信号。由于受实际的射频电路设计的限制，必存在一个最大SINR阈值门限，用τ_max=2^ν_max-1来表示，其中ν_max是最大的接收的目标速率。一旦有SINR超过了接收阈值的最大门限τ_max，那么就视为无法得到更好的速率。一般其他文献中往往使用固定的目标速率来研究一些重要的性能指标，而遍历速率是由在用户处观察到的瞬时SINR和SINR阈值来确定的。遍历总和率是指用户u_s与u_p的遍历速率之和。根据提出的方案将分析依次启用NOMA和OMA情况传输时的遍历总和率。遍历速率是频谱效率的重要指标，是指当使用自适应调制或编码实现给定瞬时SINR的香农边界时，用户可获得的平均速率。遍历速率定义为

$ \begin{gathered} \mathcal{R} = \mathbb{E}_{\varGamma}\left\{\log _{2}\left(1+\min \left\{\varGamma, \tau_{\max }\right\}\right)\right\} = \\ \frac{1}{\ln 2} \int_{0}^{\tau_{\max }} \frac{\overline{F_{\varGamma}(x)}}{1+x} d x, \end{gathered} $

(11)

其中: Γ和$\overline{F_{\varGamma}(x)}$表示用户信号加干扰噪声比和互补累计分布函数，$\mathbb{E}_{\varGamma}\{\cdot\}$表示了对SINR取数学期望。根据互补累计分布函数的定义，可以分别得出对应启用不同NOMA和OMA情况时的$\overline{F_{\varGamma}(x)}$。当启用NOMA传输时，如果传输给用户u_p的信号并由用户u_s解码，那么此时一般认为用户u_s能解码自己的信号，目标速率必能达到认为的门限。下面根据上一小节给出的传输情形依次给出计算遍历总速率所需要的互补累计分布函数。

推论1    考虑在集合Φ(R_T)中有K≥2个用户，并且空间角度差φ_ps不大于ε，即φ_ps≤ε，则根据用户在NOMA传输时的SINR，对应的互补累计分布函数可以算为和被近似为$\overline{F_{\varGamma_{s}}(x)}$和$\overline{F_{\varGamma_{p | s}}(x)}$：

$ \begin{gathered} \overline{F_{\varGamma_{s}}(x)} = \sum\nolimits_{k = 2}^{\infty} \sum\nolimits_{n = 0}^{M_{L}-1} \sum\nolimits_{m = 0}^{K-1} \frac{\varOmega(K)\left(\begin{array}{c} K-1 \\ m \end{array}\right) 2 K(-1)^{m}}{n ! \beta_{L} R_{T}^{2 m+2}}\left(\frac{M_{L} \xi_{s}(x)}{C_{L}}\right)^{-\frac{2+2 m}{\beta_{L}}} \times \\ \gamma\left(n+\frac{2 m+2}{\beta_{L}}, \frac{M_{L} \xi_{s}(x) R_{T}^{\beta_{L}}}{C_{L}}\right)\left(1-\left(1-\frac{\varepsilon}{2}\right)^{2 K-2}\right), \end{gathered} $

(12)

$ \begin{gathered} \overline{F_{\varGamma_{p | s}}(x)} \approx \sum\nolimits_{k = 2}^{\infty} \sum\nolimits_{n = 0}^{M_{L}-1} \sum\nolimits_{q_{1} = 1}^{Q_{1}} \sum\nolimits_{q_{2} = 1}^{Q_{2}} \varOmega(K)\left(\frac{M_{L} \xi_{p}(x)}{C_{L}}\right)^{-\frac{2}{\beta_{L}}} \frac{K(K-1) \varepsilon {\rm{ \mathsf{ π} }}^{2} r_{s, q_{2}} \sqrt{1-\zeta_{q_{2}}^{2}}}{n ! Q_{1} Q_{2} R_{T} \beta_{L}\left(R_{T}^{2}-r_{s, q_{2}}^{2}\right)} \\ \sqrt{1-\eta_{q_{2}}^{2}} G^{\frac{2}{\beta_{L}}}\left(\varphi_{p s, q_{1}}\right) \times\left(1-\frac{\varphi_{p s, q_{1}}}{2}\right)^{2 K-3}\left(1-\frac{r_{s, q_{2}}^{2}}{R_{T}^{2}}\right)^{K-1}\left(\gamma\left(n+\frac{2}{\beta_{L}}, \frac{M_{L} \xi_{p}(x) R_{T}^{\beta_{L}}}{G\left(\varphi_{p s, q_{1}}\right) C_{L}}\right)-\gamma\left(n+\frac{2}{\beta_{L}}, \frac{M_{L} \xi_{p}(x) r_{s, q_{2}}^{\beta_{L}}}{G\left(\varphi_{p s, q_{1}}\right) C_{L}}\right)\right), \end{gathered} $

(13)

证明  由于空间所限，证明的细节放在附录。其中，$\varOmega(K)=\frac{\left(\lambda \pi R_{T}^{2}\right)^{K}}{K !} \mathrm{e}^{-\lambda \pi R_{T}^{2}}$表示在集合Φ(R_T)内有K个用户的概率，$\xi_{s}(x)=\frac{\sigma^{2} x}{\alpha_{s} N P_{B}}, \xi_{p}(x)=$ $\frac{\sigma^{2} x}{\left(\alpha_{p}-\tau_{p} \alpha_{s}\right) N P_{B}}, \zeta_{q_{1}}=\cos \left(\frac{2 q_{1}-1}{2 Q 1}\right), \varphi_{p s, q 1}=$ $\frac{\varepsilon}{2}\left(\zeta_{q_{1}}+1\right), \eta_{q_{2}}=\cos \left(\frac{2 q_{2}-1}{2 Q_{2}} \pi\right), r_{s, q_{2}}=\frac{R_{T}}{2}\left(\eta_{q_{2}}+\right.$1)，Q₁和Q₂是利用高斯-切比雪夫求积公式引入的参数。

推论2   考虑在集合Φ(R_T)中有K≥2个用户，并且空间角度差φ_ps大于ε，即φ_ps>ε，则根据OMA传输中的SINR，对应的互补累计分布函数可以被算为和近似为$\overline{F_{\varGamma_{s}, o}(x)}$和$\overline{F_{\varGamma_{p, o}}(x)}$：

$ \begin{gathered} \overline{F_{\varGamma_{{s, o}}}(x)} = \sum\nolimits_{k = 2}^{\infty} \sum\nolimits_{n = 0}^{M_{L}-1} \sum\nolimits_{m = 0}^{K-1} \frac{\varOmega(K)\left(\begin{array}{c} K-1 \\ m \end{array}\right) 2 K(-1)^{m}}{n ! \beta_{L} R_{T}^{2 m+2}}\left(\frac{M_{L} \xi_{o}(x)}{C_{L}}\right)^{-\frac{2+2 m}{\beta_{L}}} \times \\ \gamma\left(n+\frac{2 m+2}{\beta_{L}}, \frac{M_{L} \xi_{o}(x) R_{T}^{\beta_{L}}}{C_{L}}\right)\left(1-\frac{\varepsilon}{2}\right)^{2 K-2}, \end{gathered} $

(14)

$ \begin{gathered} \overline{F_{\varGamma_{p, o}}(x)} \approx \sum\nolimits_{k = 2}^{\infty} \sum\nolimits_{n = 0}^{M_{L}-1} \sum\nolimits_{q_{2} = 1}^{Q_{2}} \varOmega(K)\left(\frac{M_{L} \xi_{o}(x)}{C_{L}}\right)^{-\frac{2}{\beta_{L}}} \frac{2 K {\rm{ \mathsf{ π} }} r_{s, q_{2}} \sqrt{1-\eta_{q_{2}}^{2}}}{n ! Q_{2} R_{T} \beta_{L}\left(R_{T}^{2}-r_{s, q_{2}}^{2}\right)}\left(1-\frac{\varepsilon}{2}\right)^{2 K-2}\left(1-\frac{r_{s, q_{2}}^{2}}{R_{T}^{2}}\right)^{K-1} \times \\ \left(\gamma\left(n+\frac{2}{\beta_{L}}, \frac{M_{L} \xi_{o}(x) R_{T}^{\beta_{L}}}{C_{L}}\right)-\gamma\left(n+\frac{2}{\beta_{L}}, \frac{M_{L} \xi_{o}(x) r_{s, q_{2}}^{\beta_{L}}}{C_{L}}\right)\right), \end{gathered} $

(15)

证明   证明的细节请参考附录。其中$\xi_{o}(x)=\frac{\sigma^{2} x}{N P_{B}}$。

特别地，当在集合Φ(R_T)中不存在一个满足所提出的用户配对条件，例如有且仅有单一用户(即K=1)时，对应的互补累计分布函数$\overline{F_{\varGamma_{s}, 1}(x)}$为

$ \begin{gathered} \overline{F_{\varGamma s, 1}(x)} = \varOmega(1) \sum\nolimits_{n = 0}^{M_{{L}^{-1}}}\left(\frac{2}{n ! \beta_{L} R_{T}^{2}}\right)\left(\frac{M_{L} \xi_{o}(x)}{C_{L}}\right)^{-\frac{2}{\beta_{L}}} \times \\ \gamma\left(n+\frac{2}{\beta_{L}}, \frac{M_{L} \xi_{o}(x) R_{T}^{\beta_{L}}}{C_{L}}\right), \end{gathered} $

(16)

推论3    考虑一个毫米波网络的下行链路使用提出的用户配对策略能适时地启用NOMA和OMA方案的传输场景，该方案的遍历总速率可以被总结为

$ \begin{gathered} \mathcal{R}_{\mathrm{sum}} = \frac{\min \left\{\tau_{\max }, \alpha_{p} / \alpha_{s}\right\} {\rm{ \mathsf{ π} }}}{2 \ln 2 Q_{4}} \sum\nolimits_{q_{4} = 1}^{Q_{4}}\\ \sqrt{1-\mu_{q_{4}}^{2}} \frac{\overline{F_{\varGamma_{p \mid s}}\left(x_{p, q_{4}}\right)}}{x_{p, q_{4}}+1}+\frac{\tau_{\max } {\rm{ \mathsf{ π} }}}{2 \ln 2 Q_{3}} \sum\limits_{q_{3} = 1}^{Q_{3}} \sqrt{1-\delta_{q_{3}}^{2}}\\ \frac{\overline{F_{\varGamma_{s}}\left(x_{s, q_{3}}\right)}}{x_{s, q_{3}}+1}+\frac{\tau_{\max } {\rm{ \mathsf{ π} }}}{2 \ln 2 Q_{3}} \times \sum\nolimits_{q_{3} = 1}^{Q_{3}} \sqrt{1-\delta_{q_{3}}^{2}}\\ \frac{\overline{F_{\varGamma_{s, o}}\left(x_{s, q_{3}}\right)}+\overline{F_{\varGamma_{p, o}}\left(x_{s, q_{3}}\right)}+\overline{F_{\varGamma_{s, 1}}\left(x_{s, q_{3}}\right)}}{x_{s, q_{3}}+1}, \end{gathered} $

(17)

其中, $\overline{F_{\varGamma_{s}}(x)}, \overline{F_{\varGamma_{p l s}}(x)}, \overline{F_{\varGamma_{s, o}}(x)}, \overline{F_{\varGamma_{p, o}}(x)}$，和$\overline{F_{\varGamma_{s, 1}}(x)}$均已经在上述推论中给出。$\varpi_{s}=$ $\cos \left(\frac{2 q_{3}-1}{2 Q_{3}} \pi\right), x_{s, q_{3}}=\frac{\tau_{\max }}{2}\left(\varpi_{s}+1\right), \quad \varpi_{p}=$ $\cos \left(\frac{2 q_{4}-1}{2 Q_{4}} \pi\right), x_{p, q_{4}}=\frac{\min \left\{\tau_{\max }, \alpha_{p} / \alpha_{s}\right\}}{2}\left(\varpi_{p}+\right.$1)。Q₃和Q₄是利用高斯-切比雪夫求积公式引入的参数。至此，本部分为数学上的严谨分析，下一节将重点用仿真实验来证明所提出方案的有效性。

4 仿真实验

这一章节中，主要介绍该方案的仿真和数值结果，并与基于距离的NOMA^[14]，基于角度的NOMA^[15]以及传统的NOMA方案^[13]和OMA方案的结果进行比较。Yi等^[14]选择离基站最近的用户，并将其与阈值距离范围内随机选择的用户配对。基站将随机选择的用户与另一个具有最小相对角度差的用户配对。在传统的NOMA方案^[13]中，离基站最近的用户将与随机选择的用户配对。OMA方案中将随机选择的用户分别进行OMA传输。另外，为了进行公平的比较，在OMA方案时，时隙的前一半和后一半，基站分别为2个用户服务。基站的发射功率为P_B=-15 dB ·mW，噪声功率为σ²=-80 dB ·mW。半径R和R_L分别设置为200和130 m。根据最近的研究成果中使用视距球模型^[11]的半径应该设在100 m左右。以下是各个仿真参数设定。设置密度λ=0.000 4/m²，β_L=3, 天线个数N=8根，C_L=2, M_L=3, ε=0.4, R_T=100 m, α_s=0.1, α_p=0.9, Q₁=Q₂=Q₃=Q₄=40，ν_s=5 bit/信道, ν_p=3 bit/信道。

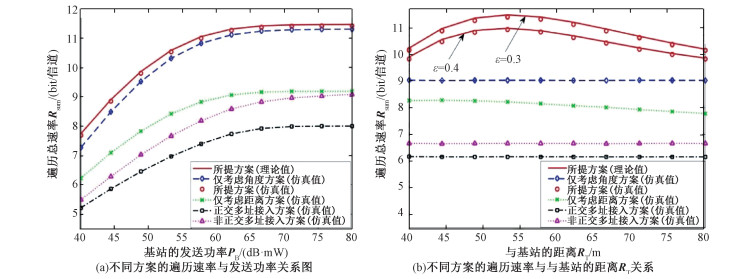
图 2表示不同方案对应的遍历速率能对比。图 2(a)表示发射功率(即P_B)对配对用户u_s和u_p的遍历总速率的影响。遍历速率是频谱效率的重要指标，在图中可以看出所提出的方案有较高的遍历和速率，其余4种均低于该方案。

从图 2(a)的结果来看，所提出的方案仿真值和理论数值结果之间的吻合验证了对其的理论分析。随着P_B的增加，用户接收到的SINR会增加，所有方案的遍历速率都随发射功率的增加而增加。最值得关注的是，所提出的方案的遍历速率高于所有其他方案，这是因为提出的基于角度和距离联合的用户配对策略同时具有了这2个重要位置信息给用户配对带来的优点。

不考虑距离的传统NOMA方案在网络性能方面优于OMA方案，并且遍历速率明显低于基于距离的NOMA方案，因此考虑用户的距离信息使得用户接收到的信噪比更好，NOMA方案的效率更高。

由图 2(b)可知，本文提出的用户配对方案中，与基站的距离和角度信息作为关键信息有重要的影响。图中2条所提出方案曲线随着角度阈值ε变小，遍历速率增加了。这是因为基于角度的用户配对策略NOMA方案在毫米波网络中充分考虑了基站的定向性波束(角度信息)使得启用NOMA的信噪比更好。总体来看，基于距离的NOMA用户配对方案性能均高于不考虑阈值范围的传统非正交多址接入方案，可见加入距离信息，遍历速率有了较明显的改善，突出了基于位置信息的配对有重要影响。而在毫米波网络中用户的传输对位置距离信息变化敏感，仅基于距离的方案，随着用户离基站的距离增加，遍历总速率呈下降趋势。最后，所提出的方案的遍历总速率曲线呈小幅度上升然后下降趋势，这是由于所提出的方案只能考虑与位于距基站一定距离内的用户配对，当距离太近用户密度较小的时候，限制了选择配对用户u_p的区域，根据提出的准则而找不到符合条件的u_p。随着R_T的增加，所提出方案的覆盖概率随着启用NOMA的概率增加而增加。当R_T超过某个阈值时，由于选择远离基站的用户的可能性更高，因此速率降低，但仍高于其他4种方案。因此，存在R_T的最优值，该最优值使配对用户遍历总速率最大化。由此可见，这2个重要的位置信息带来不可忽略的影响，充分考虑基于角度和距离联合的策略是很有必要的。

5 总结

本文讨论毫米波网络上用于下行链路非正交多址接入传输的近距离用户配对问题。提出一种基于角度和距离联合的用户配对策略，并与仅基于角度和距离的NOMA和传统不考虑位置信息的NOMA和OMA等基准方案相比，针对遍历速率评估了该方案的性能。使用随机几何对配对用户和相应的遍历速率进行了深入的数学分析。根据天线阵列等关键特征，利用了天线阵列增益而设计出的用户配对策略。结果表明，该方案下的用户遍历总速率与其他基准方案相比，具有更好的性能，并证实了在毫米波网络中考虑角度和距离信息对用户配对的重要性。最后，该方案具有更好性能的选择性接入思想以及对仿真结果的考虑与拓展是本文的亮点之处。

附录

公式(12)的证明   根据互补累积分布函数的定义可以得到$ \overline{F_{\varGamma_{s}}(x)}=\sum_{k=2}^{\infty} \varOmega(K) \mathbb{P}\left(\varGamma_{s}>x, \varphi_{p s} \leqslant\right.\varepsilon)$。再根据随机变量与其他随机变量之间的独立性，可以写成

$ \overline{F_{\varGamma_{s}}(x)} = \sum\nolimits_{k = 2}^{\infty} \varOmega(K) \mathbb{P}\left(\left|h_{s}\right|^{2}>\frac{\xi_{S}(x)}{l\left(r_{s}\right)}\right) \mathbb{P}\left(\varphi_{p s} \leqslant \varepsilon\right). $

为表示方便，$\varTheta=\mathbb{P}\left(\left|h_{s}\right|^{2}>\frac{\xi_{s}(x)}{l\left(r_{s}\right)}\right) \mathbb{P}\left(\varphi_{p s} \leqslant \varepsilon\right)$。接下来，空间角度差φ_ps的概率密度函数已经在公式(10)中给出。由公式(10)也可以得到它的累积分布函数$F_{\varphi_{i s}}(x)=1-\left(1-\frac{1}{2} \varphi\right)^{2 k-2}$，可得

$ \varTheta = \sum\nolimits_{n = 0}^{M_{L}-1} \frac{\left(M_{L} \xi_{s}(x)\right)^{n}}{n !} \mathbb{E}_{r_{s}}\left\{\frac{\exp \left(-\frac{\left(M_{L} \xi_{s}(x)\right)}{l\left(r_{s}\right)}\right)}{\left(l\left(r_{s}\right)\right)^{n}}\right\} \times F_{\varphi_{i s}}(\varepsilon). $

其中|h_s²|服从归一化的伽马分布，代入求期望时利用二项式展开可以写成$\varTheta=\sum_{n=0}^{M_{L}-1} \frac{\left(M_{L} \xi_{s}(x) / C_{L}\right)^{n}}{n !} \sum_{m=0}^{K-1}\left(\begin{array}{c} K-1 \\ m \end{array}\right)\left(-\frac{1}{R_{T}^{2}}\right)^{m} \int_{0}^{R_{T}} \frac{2 K}{R_{T}^{2}} \exp \left(-\frac{\left(M_{L} \xi_{s}(x) r_{s}^{\beta_{L}}\right.}{C_{L}}\right) r_{s}^{n \beta_{L}^{+1+2 m}} \mathrm{~d} r_{s} F_{\varphi_{i s}}(\varepsilon) $。这个积分就变得好解决了, 进而得出公式(12)。证毕。

公式(13)的证明   同样地，公式(13)的证明也按照相似的步骤，不同的是它需要对条件分布函数r_p做双重积分。$ \overline{F_{\varGamma_{p | s}}(x)}=\sum_{k=2}^{\infty} \varOmega(K) \mathbb{P}\left(\varGamma_{p |s}>x, \varphi_{p s} \leqslant \varepsilon\right)=\sum_{k=2}^{\infty} \varOmega(K) \sum_{n=0}^{M_{L}-1} \frac{\left(M_{L} \xi_{p}(x)\right)^{n}}{n !} \mathbb{E}$ $r_{s}, r_{p}, \varphi_{p s}\left\{\frac{\exp \left(-\frac{\left(M_{L} \xi_{p}(x)\right)}{G\left(\varphi_{p s}\right) l\left(r_{p}\right)}\right)}{\left(G\left(\varphi_{p s}\right) l\left(r_{p}\right)\right)^{n}}\right\} $。再接着求这样一个期望$ \mathbb{E}_{r_{s}, r_{p}, \varphi_{p}}$，三重积分展开成

$ \mathbb{E}_{r_{s}, r_{p}, \varphi_{p s}} = \int_{0}^{\varepsilon} \int_{0}^{R_{T}} \int_{r_{2}}^{R_{T}} \exp \left(-\frac{M_{L} \xi_{p}(x) r_{1}^{\beta_{L}}}{G(\varphi) C_{L}}\right)\left(G(\varphi) C_{L} r_{1}^{-\beta_{L}}\right)^{-n} \times f_{r_{p} \mid r_{s}}\left(r_{1}\right) f_{r s}\left(r_{2}\right) f_{\varphi_{p s}}(\varphi) \mathrm{d} r_{1} \mathrm{~d} r_{2} \mathrm{~d} \varphi $

通过富比尼定理，又可以处理成$\mathbb{E}_{r_{s}, r_{p}, \varphi_{p s}}=\frac{4 K\left(-\frac{M_{L} \xi_{p}(x)}{C_{L}}\right)^{-2 / \beta_{L}}}{\left(M_{L} \xi_{p}(x)\right)^{n} R_{T}^{2} \beta_{L}} \int_{0}^{E} \int_{0}^{R_{T}} \frac{r_{2} G(\varphi)^{2 / \beta_{L}}}{R_{T}^{2}-r_{2}^{2}}\left(1-\frac{r_{2}^{2}}{R_{T}^{2}}\right)^{K-1} \times $ $\left(\gamma\left(n+\frac{2}{\beta_{L}}, \frac{M_{L} \xi_{p}(x) R_{T}^{\beta_{L}}}{G(\varphi) C_{L}}\right)-\gamma\left(n+\frac{2}{\beta_{L}}, \frac{M_{L} \xi_{p}(x) r_{s, q_{2}}^{\beta_{L}}}{G(\varphi) C_{L}}\right)\right) $.

最后利用高斯-切比雪夫积分公式处理这个积分就能得到公式(13)。

公式(14)和公式(15)处理起来的过程与公式(12)和公式(13)相似，证毕。