高分辨率(high resolution, HR)图像在遥感、视频监控、医学图像、军事侦察等领域有重要应用价值。然而,图像在获取时往往会受到各种因素的影响,如距离、噪声、运动、设备抖动和欠采样等,导致分辨率受限,不能满足当前空间图像应用的要求。因此,提升图像的分辨率至关重要。超分辨率重建通过信号处理的方式,融合多帧具有亚像素位移的低分辨率(low resolution, LR)图像,估计出HR图像。该技术可以有效地克服硬件成像分辨率的限制。
1984年Tsai和Huang[1]首先提出频域超分辨率重建方法,并应用于卫星图像。此后,国内外学者对超分辨率重建技术进行后续研究,提出更有效的超分辨重建方法[2]。目前,超分辨率重建算法主要是在空间域上实现分辨率的提升,可分为基于插值、基于学习和基于建模3大类方法。基于插值的方法[3]是利用已知的相邻像素来估计未知的像素,优点是计算量较小,但该方法未考虑局部几何结构相似性等信息,会引入“锯齿”、“马赛克”等虚假信息,造成边缘不清晰,图像整体模糊。基于学习的方法[4]利用训练数据集学习LR图像和HR图像之间的映射关系预测HR图像,重建结果优于基于建模的方法。然而学习过程需要足够多的图像数据,算法一般针对特定类型的图像进行处理,在帧数有限的LR图像序列中难以满足。基于建模的方法从影响图像成像因素出发,建立退化模型进行重建。基于建模的方法在求解时,可以加入先验信息对重建问题进行约束,将病态的超分辨率重建问题转化为良性问题,成为超分辨率重建的主流方法之一。该方法主要包括迭代反投影(iterate back projection, IBP)法[5]、凸集投影(projection onto convex sets, POCS)法[6-7]和最大后验(maximum a posteriori, MAP)概率方法[8-10]等。IBP方法简单直观,可用于复杂运动的退化模型,但此方法不易加入先验,无法求得唯一的解。POCS方法可得到锐利的边缘和清晰的纹理,且加入先验方便,然而解依赖于初始值的设定,算法的计算量大,收敛速度和稳定性也有待提升。MAP方法尽管计算量较大,收敛速度较慢,但易于引入先验,确保解存在且唯一,是一种较优的重建方法。
在基于建模的方法中,添加的先验模型主要包括Tikhonov先验模型[11]和TV先验模型[12-13]及其改进先验模型。Tikhonov先验模型易于优化,而先验项限制了高频分量,重建图像无法得到锐利的边缘。TV先验模型因其保边性能好,是应用较多的先验模型之一。然而,该模型不能根据图像在不同区域的特性实现自动处理,导致在平坦区域存在“阶梯效应”。对此,Yuan等[14]根据图像的空间信息进行加权限制,提出空间加权(spatially weighted total variation,SWTV)正则化算法,有效改善重建图像的“阶梯效应”。Villena等[15]进一步优化TV先验模型,从梯度图像的水平方向和垂直方向选取不同权重值,提出L1先验模型,有效保持边缘的同时平滑图像,但此算法在平滑离散区域噪声时表现效果不佳。
基于上述分析,为重建出边缘保持且噪声低的HR图像,对L1先验模型进行改进,提出联合L1和L0先验模型的超分辨率重建算法。利用L0范数[16-17]的稀疏性,锐化图像的主要边缘而去除幅度较小的纹理或噪声,以去除因“阶梯效应”产生的噪声。将本文算法与双三次插值、TV先验模型和L1先验模型作对比,通过仿真实验数据和真实实验数据的分析,从客观评价指标和主观评价指标上证实本文算法重建的HR图像质量更高。
1 基于MAP的超分辨率重建在图像的获取过程中,许多因素会导致图像质量下降,得到低分辨率图像。在经典的退化模型中,影响因素有运动形变、模糊、下采样和噪声,其数学表达式如下
| $ \boldsymbol{y}_{i}=\boldsymbol{A} \boldsymbol{B} \boldsymbol{W}_{i} \boldsymbol{x}+\boldsymbol{n}_{i},(i=1,2, \cdots, k), $ | (1) |
式中:
超分辨率重建是上述退化过程的逆过程,是一个典型的病态问题。本文采用MAP方法对x进行估计:
| $ \hat{\boldsymbol{x}}=\underset{\boldsymbol{x}}{\operatorname{argmax}} p(\boldsymbol{x} \mid \boldsymbol{y})=\underset{\boldsymbol{x}}{\operatorname{argmax}} \frac{p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x})}{p(\boldsymbol{y})}, $ | (2) |
式中:
| $ \hat{\boldsymbol{x}}=\underset{\boldsymbol{x}}{\operatorname{argmin}}(-\log p(\boldsymbol{y} \mid \boldsymbol{x})-\log p(\boldsymbol{x})). $ | (3) |
假设第i帧图像的噪声是均值为0且方差为(2βi)-1的高斯白噪声,则每帧LR图像对应的条件概率p(yi|x)表示为
| $ p\left(\boldsymbol{y}_{i} \mid \boldsymbol{x}, {\beta}_{i}\right) \propto \beta_{i}{}^{\frac{m n}{2}} \exp \left\{-\beta_{i}\left\|\boldsymbol{y}_{i}-\boldsymbol{A} \boldsymbol{B} \boldsymbol{W}_{i} \boldsymbol{x}\right\|_{2}^{2}\right\} . $ | (4) |
假设LR图像序列之间的噪声是独立同分布的,则条件概率p(y|x)为
| $ p(\boldsymbol{y} \mid \boldsymbol{x}, \beta)=\prod\limits_{i=1}^{k} p\left(\boldsymbol{y}_{i} \mid \boldsymbol{x}, {\beta}_{i}\right). $ | (5) |
先验概率p(x)可以减少对x估计的不确定性,从而得到稳定的重建结果。结合L1先验模型pL1(x) 的保边特性和L0先验模型pL0(x)的去噪特性,本文提出混合先验模型p(x)=pL1 (x)pL0(x)。其中,L1先验模型的概率密度函数如下
| $ \begin{gathered} p_{L_{1}}\left(\boldsymbol{x} \mid \alpha^{\mathrm{h}}, \alpha^{\mathrm{v}}\right) \propto\left(\alpha^{\mathrm{h}} \alpha^{\mathrm{v}}\right)^{M N} \exp \left\{-\left[\alpha^{\mathrm{h}}\left\|\Delta^{\mathrm{h}}(\boldsymbol{x})\right\|_{1}+\right.\right. \\ \left.\left.\alpha^{\mathrm{v}}\left\|\varDelta^{\mathrm{v}}(\boldsymbol{x})\right\|_{1}\right]\right\}, \end{gathered} $ | (6) |
式中:Δih(x) 表示HR图像在像素点i处水平方向的一阶差分,Δiv(x) 表示HR图像在像素点i处垂直方向的一阶差分,αh和αv分别是水平方向和垂直方向的模型参数。
L0先验模型的概率密度函数如下
| $ p_{L_{0}}(\boldsymbol{x} \mid \lambda) \propto \lambda^{M N} \exp \{-\lambda C(\boldsymbol{x})\}, $ | (7) |
式中:C(x)=‖Δ(x)‖0表示HR图像的梯度图像中非零元素的个数,λ是参数。
因此,将式(5)、式(6)和式(7)代入式(3)得目标函数
| $ \begin{gathered} \min \limits_{\boldsymbol{x}} \beta\|\boldsymbol{y}-\boldsymbol{A} \boldsymbol{B} \boldsymbol{W} \boldsymbol{x}\|_{2}^{2}+\alpha^{\mathrm{h}}\left\|\varDelta^{\mathrm{h}}(\boldsymbol{x})\right\|_{1}+ \\ \alpha^{\mathrm{v}}\left\|\varDelta^{\mathrm{v}}(\boldsymbol{x})\right\|_{1}+\lambda C(\boldsymbol{x}), \end{gathered} $ | (8) |
式中:β‖y-ABWx‖22是数据保真项,αh‖Δh(x)‖1+ αv‖Δv(x)‖1是L1先验项,λC(x)是L0先验项。
2 联合L1和L0先验模型的超分辨率重建算法L1先验项和L0先验项无法直接应用梯度下降法,采用majorization-minimization(MM)算法[12]和the half-quadratic splitting L0 minimization method[16]分别对L1先验项和L0先验项进行优化。
2.1 L1先验项的优化MM算法的准则是找到目标函数的一个易于优化的上界函数,通过优化该上界函数获得原问题的解。首先考虑以下不等式,对任意的a≥0和b≥0有
| $ \sqrt{a} \leqslant \sqrt{b}+\frac{a-b}{2 \sqrt{b}}, $ | (9) |
然后,对L1先验项应用不等式(9),则L1先验项的上界函数可表示为
| $ \begin{gathered} Q_{L 1}\left(\boldsymbol{x} \mid \boldsymbol{x}^{(t)}\right)=\sum\limits_{i=1}^{M N} \alpha^{\mathrm{h}}\left\|\varDelta_{i}^{\mathrm{h}}\left(\boldsymbol{x}^{(t)}\right)\right\|_{1}+ \\ \sum\limits_{i=1}^{M N} \alpha^{\mathrm{v}}\left\|\varDelta_{i}^{\mathrm{v}}\left(\boldsymbol{x}^{(t)}\right)\right\|_{1}+ \\ \alpha^{\mathrm{h}} \sum\limits_{i}^{M N} \frac{\left(\varDelta_{i}^{\mathrm{h}}(\boldsymbol{x})\right)^{2}-\left(\varDelta_{i}^{\mathrm{h}}\left(\boldsymbol{x}^{(t)}\right)\right)^{2}}{2 \sqrt{\left(\varDelta_{i}^{\mathrm{h}}\left(\boldsymbol{x}^{(t)}\right)\right)^{2}}}+ \\ \alpha^{\mathrm{v}} \sum\limits_{i}^{M N} \frac{\left(\varDelta_{i}^{\mathrm{v}}(\boldsymbol{x})\right)^{2}-\left(\varDelta_{i}^{\mathrm{v}}\left(\boldsymbol{x}^{(t)}\right)\right)^{2}}{2 \sqrt{\left(\varDelta_{i}^{\mathrm{v}}\left(\boldsymbol{x}^{(t)}\right)\right)^{2}}}, \end{gathered} $ | (10) |
式中:x(t)表示当前迭代图像。令
| $ Q_{L_{1}}\left(\boldsymbol{x} \mid \boldsymbol{x}^{(t)}\right)=\boldsymbol{x}^{\mathrm{T}} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{U}^{(t)} \boldsymbol{D} \boldsymbol{x}+c^{t e}, $ | (11) |
式中:cte为常数项。
2.2 L0先验项的优化参考文献[16]所提的the half-quadratic splitting L0 minimization method算法,对L0范数引入增广变量进行优化,则λC(x) 变换为
| $ \lambda C(\boldsymbol{H}, \boldsymbol{V})+\gamma\left\|\boldsymbol{H}-\boldsymbol{D}^{\mathrm{h}} \boldsymbol{x}\right\|_{2}^{2}+\gamma\left\|\boldsymbol{V}-\boldsymbol{D}^{\mathrm{v}} \boldsymbol{x}\right\|_{2}^{2}, $ | (12) |
式中:C(H, V)= #{p‖Hp| + |Vp|≠0}表示|Hp|+ |Vp|在p处不为零的个数。当参数γ趋于无穷大时,H趋近于水平方向的梯度图像Dhx,V趋近于垂直方向的梯度图像Dvx。此时,C(H, V)的非零元素个数趋近于C(x)的非零元素个数。
将式(11)和式(12)代入式(8)得目标优化函数:
| $ \begin{gathered} Q\left(\boldsymbol{x} \mid \boldsymbol{x}^{(t)}\right)=\beta\|\boldsymbol{y}-\boldsymbol{A} \boldsymbol{B} \boldsymbol{W} \boldsymbol{x}\|_{2}^{2}+Q_{L_{1}}\left(\boldsymbol{x} \mid \boldsymbol{x}^{(t)}\right)+ \\ \lambda C(\boldsymbol{H}, \boldsymbol{V})+\gamma\left\|\boldsymbol{H}-\boldsymbol{D}^{\mathrm{h}} \boldsymbol{x}\right\|_{2}^{2}+ \\ \gamma\left\|\boldsymbol{V}-\boldsymbol{D}^{\mathrm{v}} \boldsymbol{x}\right\|_{2}^{2}, \end{gathered} $ | (13) |
对式(13)进行分步求解:
1) 求解HR图像x(t+1):
| $ \begin{aligned} \boldsymbol{x}^{(t+1)}=&\underset{\boldsymbol{x}}{\arg \min } \beta\|\boldsymbol{y}-\boldsymbol{A} \boldsymbol{B} \boldsymbol{W} \boldsymbol{x}\|_{2}^{2}+Q_{L_{1}}\left(\boldsymbol{x} \mid \boldsymbol{x}^{(t)}\right)+\\ &\gamma\left\|\boldsymbol{H}-\boldsymbol{D}^{\mathrm{h}} \boldsymbol{x}\right\|_{2}^{2}+\gamma\left\|\boldsymbol{V}-\boldsymbol{D}^{\mathrm{v}} \boldsymbol{x}\right\|_{2}^{2}, \end{aligned} $ | (14) |
2) 求解辅助变量H和V:
| $ \begin{gathered} (\boldsymbol{H}, \boldsymbol{V})=\underset{(\boldsymbol{H}, \boldsymbol{V})}{\arg \min } \lambda C(\boldsymbol{H}, \boldsymbol{V})+\gamma\left\|\boldsymbol{H}-\boldsymbol{D}^{\mathrm{h}} \boldsymbol{x}\right\|_{2}^{2}+ \\ \gamma\left\|\boldsymbol{V}-\boldsymbol{D}^{\mathrm{v}} \boldsymbol{x}\right\|_{2}^{2}, \end{gathered} $ | (15) |
基于上述分析,联合L1和L0先验模型的超分辨率重建算法如算法1所示。
Algorithm 1 image SR reconstruction algorithm by combining l1 and 10 prior model
Input: sequenses yi, i=1, 2, …, k
1:
2: choose blur matrix H
3: estimate registration matrix W and parameters β, αh, αv
4: for t: =0 to maxiter do
5:
U(t): = diag [Uh(t)Uv(t)]
6: initialize γ0, γmax, λ
7:
for γ: =γ0 to γmax do
8: with x(t), solve H and V with equation (15)
9: with H and V, solve x(t+1) with equation (14) by Preconditioned Conjugate Gradients algorithm
10:
end for
11:
if ‖x(t+1)-x(t)‖2/
‖x(t)‖2 < le-5 then
12: break
13:
end if
14: update W, β, αh, α
15: end for
Output:
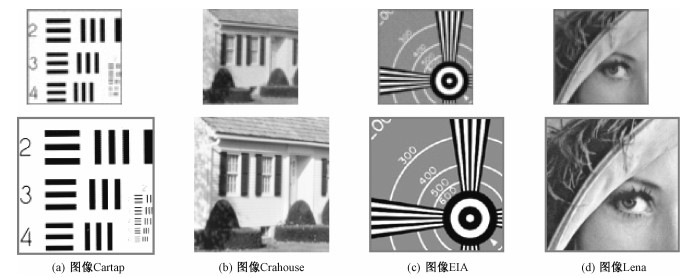
实验部分包含仿真实验数据和真实实验数据的分析, 选取双三次插值、TV先验模型、L1先验模型作为对比算法。仿真实验数据选取4幅124×124 HR图像,即图像Cartap、图像Crahouse、图像EIA和图像Lena,相应的参考LR图像和HR图像如图 1所示。其中LR图像序列由HR图像经过以下步骤获得:
|
Download:
|
| 图 1 仿真测试图像的LR图像及其相应的HR图像 Fig. 1 LR images and its corresponding HR images of simulations | |
1) 随机地平移旋转;
2) 使用3×3的均值模糊算子进行模糊退化;
3) 隔行隔列下采样;
4) 根据信噪比(signal-noise ratio, SNR)加入高斯噪声。
在估计
仿真实验采用峰值信噪比(peak signal-to-noise ratio, PSNR)和结构相似性指数(structure similarity index measure, SSIM)来评价算法的性能。PSNR值越高表明重建图像的信噪比越高,质量越好。SSIM值越接近1,表明2幅图像的结构相似性越高。
表 1给出SNR=30 dB时,本文算法与对比算法的PSNR和SSIM结果对比。由表 1可看出,本文算法的PSNR和SSIM均高于被对比算法。图 2给出与表 1一致的重建结果对比图。由图 2可看出,本文算法在保持边缘的同时,在非边缘区域的去噪效果更优,尤其是非边缘区域较多的图像Cartap和图像EIA。
|
|
表 1 不同算法的超分辨率重建结果对比 Table 1 Comparison of SR reconstruction results with different methods |
真实实验数据选取8帧100×100 LR图像Car、16帧100×100 LR图像Noel、30帧49×57 LR图像Text、15帧66×76 LR图像Adyoron和10帧256×256 LR图像Plant。实验结果如下所示,图 3为上述图像的参考LR图像,图 4至图 8分别是图像Car、图像Noel、图像Text、图像Adyoron和图像Plant的超分辨率重建结果对比图。

|
Download:
|
| 图 3 真实LR图像 Fig. 3 Real LR images | |

|
Download:
|
| 图 4 图像Car的超分辨率重建结果图 Fig. 4 SR reconstruction results of "Car" image | |
|
Download:
|
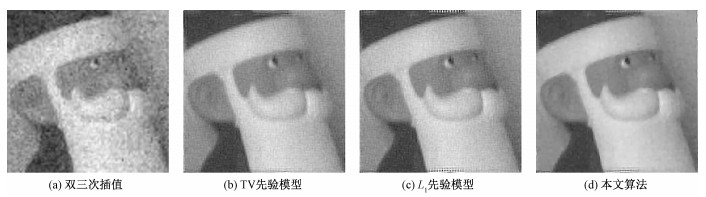
| 图 5 图像Noel的超分辨率重建结果图 Fig. 5 SR reconstruction results of "Noel" image | |

|
Download:
|
| 图 6 图像Text的超分辨率重建结果图 Fig. 6 SR reconstruction results of "Text" image | |
|
Download:
|
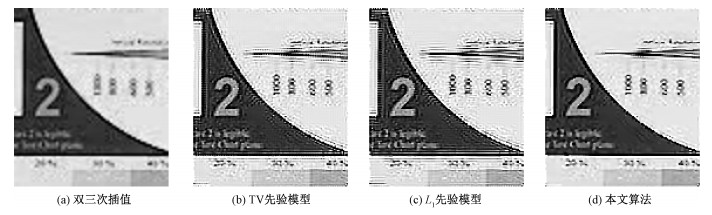
| 图 7 图像Adyoron的超分辨率重建结果图 Fig. 7 SR reconstruction results of "Adyoron" image | |

|
Download:
|
| 图 8 图像Plant的超分辨率重建结果图 Fig. 8 SR reconstruction results of "Plant" image | |
从图 4至图 8对比可看出,双三次插值的结果图边缘不清晰,噪声明显,图像整体模糊。TV先验模型和L1先验模型重建的边缘较好(如图 4 Car车窗上的字母和图 5 Noel的鼻子和耳朵),然而在非边缘区域存在“阶梯效应”(如图 4和图 5的白色区域,图 7的平坦区域和图 8的放大部分)。相比之下,本文算法的保边效果不低于TV先验模型和L1先验模型(如图 6中字母边缘部分),且在非边缘区域噪声抑制效果明显。
4 结论本文针对L1先验模型存在的“阶梯效应”,提出联合L1和L0先验模型的超分辨率重建算法。实验结果表明,本文算法的PSNR和SSIM值高于双三次插值、TV先验模型和L1先验模型,重建结果的保边效果和去噪效果优于被对比算法,有效提高超分辨率重建图像的质量。而本文算法因L0先验模型的引入,该先验的参数无法实现自动化求解,可进一步研究探讨。
| [1] |
Tsai R, Huang T S. Multiframe image restoration and registration[J]. Advances in Computer Vision and Image Processing, 1984, 1(2): 317-339. |
| [2] |
Yue L W, Shen H F, Li J, et al. Image super-resolution: the techniques, applications, and future[J]. Signal processing, 2016, 128(11): 389-408. Doi:10.1016/j.sigpro.2016.05.002 |
| [3] |
Zhang Y F, Fan Q L, Bao F X, et al. Single-Image super-resolution based on rational fractal interpolation[J]. IEEE Transactions on Image Processing, 2018, 27(8): 3782-3797. Doi:10.1109/TIP.2018.2826139 |
| [4] |
Yang W M, Zhang X C, Tian Y P, et al. Deep learning for single image super-resolution: a brief review[J]. IEEE Transactions on Multimedia, 2019, 21(12): 3106-3121. Doi:10.1109/TMM.2019.2919431 |
| [5] |
刘克俭, 陈淼焱, 冯琦. 一种优化的迭代反投影超分辨率重建方法[J]. 遥感信息, 2019, 34(3): 14-18. Doi:10.3969/j.issn.1000-3177.2019.03.003 |
| [6] |
陈健, 王伟国, 刘廷霞, 等. 基于梯度图的快速POCS超分辨率复原算法研究[J]. 仪器仪表学报, 2015, 36(2): 327-338. Doi:10.19650/j.cnki.cjsi.2015.02.011 |
| [7] |
Liu J S, Dai S S, Guo Z Y, et al. An improved POCS super-resolution infrared image reconstruction algorithm based on visual mechanism[J]. Infrared Physics & Technology, 2016, 78: 92-98. Doi:10.1016/j.infrared.2016.07.010 |
| [8] |
Liu C, Sun D Q. On Bayesian adaptive video super resolution[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(2): 346-360. Doi:10.1109/TPAMI.2013.127 |
| [9] |
Chen J, Nunez-Yanez J L, Achim A. Bayesian video super-resolution with heavy-tailed prior models[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2014, 24(6): 905-914. Doi:10.1109/TCSVT.2014.2302549 |
| [10] |
Zhang Q P, Zhang Y, Mao D Q, et al. A Bayesian super-resolution method for forward-looking scanning radar imaging based on split bregman[C]//2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2018). July 22-27, 2018, Valencia, Spain. IEEE, 2018: 5135-5138. DOI: 10.1109/IGARSS.2018.8518359.
|
| [11] |
Jiang J J, Chen C, Huang K B, et al. Noise robust position-patch based face super-resolution via Tikhonov regularized neighbor representation[J]. Information Sciences, 2016, 367/368: 354-372. Doi:10.1016/j.ins.2016.05.032 |
| [12] |
Bioucas-Dias J M, Figueiredo M A T, Oliveira J P. Total variation-based image deconvolution: a majorization-minimization approach[C]//2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings. May 14-19, 2006, Toulouse, France. IEEE, 2006: 861-864. DOI: 10.1109/ICASSP.2006.1660479.
|
| [13] |
Yuan Q Q, Zhang L P, Shen H F. Regional spatially adaptive total variation super-resolution with spatial information filtering and clustering[J]. IEEE Transactions on Image Processing, 2013, 22(6): 2327-2342. Doi:10.1109/TIP.2013.2251648 |
| [14] |
Yuan Q Q, Zhang L P, Shen H F. Multiframe super-resolution employing a spatially weighted total variation model[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2012, 22(3): 379-392. Doi:10.1109/TCSVT.2011.2163447 |
| [15] |
Villena S, Vega M, Molina R, et al. Bayesian super-resolution image reconstruction using an ℓ1 prior[C]//2009 Proceedings of 6th International Symposium on Image and Signal Processing and Analysis. September 16-18, 2009, Salzburg, Austria. IEEE, 2009: 152-157. DOI: 10.1109/ISPA.2009.5297740.
|
| [16] |
Xu L, Lu C W, Xu Y, et al. Image smoothing via L0 gradient minimization[J]. ACM Transactions on Graphics, 2011, 30(6): 1-12. Doi:10.1145/2070781.2024208 |
| [17] |
张剑, 刘萍萍. 基于L0范数和稀疏编码的单幅图像超分辨率重建方法[J]. 电子测量与仪器学报, 2018, 32(11): 194-201. Doi:10.13382/j.jemi.2018.11.026 |
| [18] |
He Y, Yap K H, Chen L, et al. A nonlinear least square technique for simultaneous image registration and super-Resolution[J]. IEEE Transactions on Image Processing, 2007, 16(11): 2830-2841. Doi:10.1109/TIP.2007.908074 |
 2022, Vol. 39
2022, Vol. 39 



