2. 中国科学院上海微系统与信息技术研究所, 上海 200050;
3. 中国科学院大学, 北京 100049
2. Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 200050, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
随着物联网时代信息的快速增长,用户对数据处理速率、服务质量(quality of service, QoS) 与体验质量(quality of experience, QoE)的要求在不断提高。然而大批提升用户体验的智能应用服务,如增强现实(augmented reality, AR)、虚拟现实(virtual reality, VR)、交互游戏等往往伴随着高计算复杂度和低时延的要求。因此即使移动设备的处理能力在不断提高,但智能手机作为便携性设备,由于其固有的缺点,如有限的计算资源、存储资源,仍然无法满足此类任务的要求。移动边缘计算能够有效平衡设备能力和用户体验的困境,同时,移动边缘计算的安全性能够得到保障,如文献[1]中作者从服务器安全、用户隐私等多方面来保证系统的稳定。因此移动边缘计算技术被广泛研究。在移动边缘计算(mobile edge computing, MEC)网络中[2-4],将高计算复杂度的任务卸载至网络边缘端,利用分布式的计算资源和存储资源,能够有效减少任务的处理时延。因此,如何实现更高效的任务卸载吸引了大量学者的关注。
在许多文献中,任务卸载被建模为确定性优化问题。You等[5]在任务计算时延的约束下,通过任务卸载实现最小化能量消耗,并将该任务卸载问题定义为确定性优化问题。然而一个实用的任务卸载策略应该能够根据系统的实时状态进行自主调整,例如用户设备的队列信息、帮助节点的计算能力等。基于该考虑,Mao等[6]将任务卸载建模为随机规划问题,利用李雅普诺夫优化方法,将复杂的随机规划问题转换为一系列简单的顺序决策问题。上述文献提出的任务卸载策略都是基于系统参数信息已知的假设,但在实际场景中用户难以获得系统信息,或者需要大量开销来获取信息,因此需要一个能够自主在线学习的策略实现任务卸载。此外,在文献[5-6]中,作者只根据系统的短期利益更新任务卸载策略,而忽略了系统的长远利益。本文将针对这2个因素来建立任务卸载模型。
强化学习作为一种在线学习方法,能够从系统历史反馈中学习系统信息,从而处理系统的未知性。近期许多文献利用强化学习技术在任务卸载方面取得进展。Chen等[7]利用强化学习得到更优的任务卸载策略,从而实现系统长期效用的最大化。Min等[8]将能量收集技术应用到MEC网络,通过强化学习来选择卸载节点和速率以提高用户体验。Huang等[9]将无线供电MEC网络的任务卸载建模为组合优化问题,利用强化学习得到近似最优解。然而,上述文献都是基于静止的用户设备,忽视了移动用户的需求,无法应用于移动场景,如现在的车联网(vehicle-to-everything, V2X)应用、AR的场景导览、移动机器人[10]等,因此针对于移动用户的任务卸载的研究具有重要意义。
相较于移动的用户,静止用户所处的MEC网络环境中的信道环境、周围节点的拓扑结构等比较稳定,这也是之前大部分研究任务卸载的文献中考虑的场景[4-8]。而相比于传统有线网络,如今很多使用无线网络、蜂窝网络的用户通常处于移动状态,因此不仅用户周围的帮助节点会随着变化,信道状态也会发生改变。基于此考虑,本文参照文献[11]中MEC网络的拓扑结构和用户移动模式,假设用户按照马尔科夫性质在网络中移动,利用强化学习技术对任务卸载进行研究。文献[11]中,在一个蜂窝网络完全覆盖、Wi-Fi局部覆盖的场景中,作者探究在昂贵的蜂窝网络和便宜的Wi-Fi下,移动用户通过Wi-Fi卸载来减少开销从而完成长时间的文件传输。他们将卸载模型定义为马尔科夫决策过程(Markov decision process, MDP),并在用户移动模式已知时提供系统最优解。MDP被广泛应用于随机规划问题中,它能够有效地刻画系统的动态变化,并将系统的长期表现作为目标。
本文将移动用户的任务卸载问题建模为MDP,并在系统信息为先验知识时,提供系统的最优解。同时,在系统信息未知,即用户移动模式未知时,通过基于Q-learning和DQN的在线学习方法,得到收敛速度快,且效果逼近最优解的算法。
符号说明:指示函数1{A}表示事件A发生(不发生)时取值为1(0)。
在移动边缘计算网络中(参见图 1),存在移动用户(本地节点)和一些固定节点。固定节点可以是宏基站、微基站和家庭基站等,它们能够为用户设备提供计算资源和存储资源等,后文将其称为帮助节点。

|
Download:
|
| 图 1 移动边缘计算的网络拓扑结构图 Fig. 1 Topology of the MEC network | |
参照文献[11]的场景设置,将移动边缘计算的网络场景离散化为L个方格(位置),每个方格用l表示,
① 以图 1为例, 当用户移动至场景中的左上角时, 相比于卸载至计算能力强但通信距离较远的宏基站, 若卸载到离用户设备更近的帮助节点, 可能会实现更低的时延。
由于单一节点的计算和存储资源有限,在本地处理的任务通常会经历较高延迟,影响用户服务质量。为实现低延迟处理,本地节点可以将部分计算任务卸载到周围的帮助节点,这些帮助节点通常拥有更多的计算和存储资源,并且可以按需部署以实现更高要求。在这个任务卸载模型中,考虑T个时隙
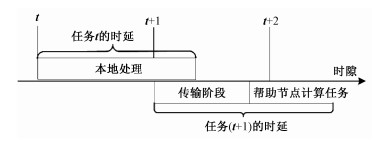
|
Download:
|
| 图 2 任务卸载模型时间线 Fig. 2 Timeline example of task offloading | |
本文的目标是最小化移动用户的长期任务时延。为刻画用户移动性带来的系统随机性,将问题定义为一个马尔科夫决策过程,利用系统转移概率来刻画用户的移动模式。该问题可以由4个元素完全表征,下面将分别介绍。
1) 系统状态
| $ \mathcal{B}=\left\{0, \mu, \mu-f^{0}, \cdots, m \cdot \mu-n \cdot f^{0}, \cdots, B\right\}. $ |
其中:m, n为正整数,f0为本地节点计算能力,即每时隙处理的任务大小。当任务在本地计算时,队列会增加大小为μ的任务,同时本地节点以f0的速度处理任务。当任务卸载到其他帮助节点时,本地节点不增加任务,同时以f0的速度处理任务。
2) 动作
3) 转移概率
| $ \begin{gathered} \mathbb{P}\left(s_{t+1} \mid s_{t}, a_{t}\right) = \mathbb{P}\left(l_{t+1}, b_{t+1} \mid l_{t}, b_{t}, a_{t}\right) = \\ \mathbb{P}\left(l_{t+1} \mid l_{t}\right) \mathbb{P}\left(b_{t+1} \mid l_{t}, b_{t}, a_{t}\right), \end{gathered} $ | (1) |
其中bt+1的转移概率服从
| $ \begin{gathered} \mathbb{P}\left(b_{t+1} \mid l_{t}, b_{t}, a_{t}\right) = \\ \begin{cases}1, & b_{t+1} = \left[b_{t}+\mu \cdot 1\left\{a_{t} = 0\right\}-f^{0}\right]^{+}, b_{t+1} \leqslant B, \\ 0, & \text { else },\end{cases} \end{gathered} $ | (2) |
4) 开销c(s, a):系统的开销定义为完成任务需要的时延,c(st, at)为完成任务t所需要的时延
| $ c\left(s_{t}, a_{t}\right) = \frac{\mu+b}{f\left(l_{t}, a_{t}\right)}+\frac{\mu \cdot 1\left\{a_{t} \in \mathcal{A} \backslash\{0\}\right\}}{r\left(l_{t}, a_{t}\right)}, $ | (3) |
等式右边的第1项为任务t的处理时延,第2项为传输时延,类似大多数文献的考虑[5-6],本文也忽略任务结果传输回本地节点的时间。f(lt, at)为用户位于lt时卸载到的节点at的计算能力,即节点at的计算速度。注意当at=0时,f(lt, at)=f0;当at≠0时b=0。r(lt, at)为传输速率,只有将任务卸载给帮助节点,即
为最小化移动用户的长期任务的时延,将问题定义为
| $ \min \limits_{\pi \in \Pi} \mathbb{E}\left[\sum\limits_{t = 1}^{T} \gamma^{t-1} c\left(s_{t}, \pi\left(s_{t}\right)\right)\right]. $ | (4) |
其中:π为
当系统信息已知,即转移概率
| $ V_{\pi}(s) = \mathbb{E}\left[\sum\limits_{t = i+1}^{T} \gamma^{t-1} c\left(s_{t}, a_{t}\right) \mid s_{i} = s\right], \forall s \in \mathcal{S}, $ | (5) |
其中:si代表初始状态,
最优策略π*的状态值函数Vπ*(s)称为最优状态值函数,下文简写为V*(s)。最优状态值函数满足贝尔曼最优性条件[14],以系统状态st为例:
| $ V^{*}\left(s_{t}\right) = \min \limits_{a \in \mathcal{A}} Q^{*}\left(s_{t}, a\right), $ | (6) |
其中Q*(st, a)为状态-动作对(st, a)的动作值函数,满足
| $ \begin{aligned} Q^{*}\left(s_{t}, a\right) & = \mathbb{E}\left[c\left(s_{t}, a\right)+\gamma V^{*}\left(s^{\prime}\right) \mid s_{t}, a\right] \\ & = c\left(s_{t}, a\right)+\gamma \sum\limits_{s^{\prime} \in \mathcal{S}} \mathbb{P}\left(s^{\prime} \mid s_{t}, a\right) V^{*}\left(s^{\prime}\right) \\ & = \frac{\mu+b}{f\left(l_{t}, a\right)}+\frac{\mu \cdot 1\{a \in \mathcal{A} \backslash\{0\}\}}{r\left(l_{t}, a\right)}+\\ &\gamma \sum\limits_{l^{\prime} \in \mathcal{L}, b^{\prime} \in \mathcal{B}} \mathbb{P}\left(l^{\prime} \mid l\right) \mathbb{P}\left(b^{\prime} \mid l_{t}, b_{t}, a\right) V^{*}\left(s^{\prime}\right), \end{aligned} $ | (7) |
其中s′为系统在状态st执行动作a后,系统可能转移的下一状态。式(7)中第2个等式的第1项为任务t的即时开销c(st, a),第2项为对未来所有任务的折扣开销的期望的估计,γ是1.2节中的折扣因子,满足γ < 1。在贝尔曼最优性方程中,即时开销的比重为1,高于对未来开销的估计的比重γ。
动作值函数Q*(s, a)的定义与状态值函数V*(s)相似,为系统在状态s执行动作a后,按照策略π*实现的长期折扣开销的期望。从式(6)可以看出,若已知最优动作值函数Q*(s, a),采用贪婪算法执行任务卸载,即最低动作值函数对应的动作为最优卸载决策
| $ \pi^{*}(s) = \underset{a \in \mathcal{A}}{\arg \min } Q^{*}(s, a), \forall s \in \mathcal{S} . $ | (8) |
基于以上研究,当系统信息已知时,通过数值迭代能够求解所有状态-动作对的最优动作值函数,再基于贪婪算法获得最优策略。具体流程见算法1。
算法1 最优任务卸载算法
输入:
步骤1) 初始化策略π*(s)和状态值函数
步骤2) 对
步骤3) 若b≤B,对
步骤4) 若b>B,对
步骤5) 根据式(7)更新Q*(s, a),根据式(8)更新π*(s),按照式(6)设置V*(s)。
步骤6) 若V*(s)收敛,算法结束;否则跳转至步骤2。
输出:最优任务卸载策略
算法1通过离线地对贝尔曼最优性条件,式(6)和式(7),进行数值迭代,从而得到最优卸载策略π*。当系统需要进行在线任务卸载时,观测到状态s后,可以直接通过π*(s)获得最优卸载决策。
2.2 在线任务卸载算法然而系统信息一般难以获得,虽然能够根据用户的历史移动轨迹,对用户移动模式进行预测[12-13],但会引入大量额外开销。为解决用户移动性带来的系统未知性,基于在线学习,提出能够应对用户移动性的任务卸载算法。
2.2.1 基于Q-learning的任务卸载由于用户移动模式为后验知识,无法通过2.1节中的算法得到最优任务卸载策略,因此需要在线学习的算法来处理未知信息。Q-learning作为一种无模型方法,可以根据系统的历史反馈,对动作值函数Q(s, a)进行预测。
在系统状态st时执行动作at后,观测系统开销c(st, at),同时系统转移到下一状态st+1,可以将这些信息称为一组经验值et=(st, at, c(st, at), st+1)。之后动作值函数Q(st, at)利用这一组经验值,按照下式更新:
| $ \begin{aligned} &Q_{t}\left(s_{t}, a_{t}\right) = \left(1-\alpha_{t}\right) Q_{t-1}\left(s_{t}, a_{t}\right)+ \\ &\alpha_{t}\left(c\left(s_{t}, a_{t}\right)+\min \limits_{a \in \mathcal{A}} Q_{t-1}\left(s_{t+1}, a\right)\right), \end{aligned} $ | (9) |
式中:Qt为动作值函数的第t次迭代,αt为第t次迭代的学习率,也代表此次经验值et的重要性。在每个时隙,系统利用经验值更新动作值函数,获得新的动作值函数后,在下一时隙根据新的动作值函数按照式(8)执行卸载决策。
根据文献[14-15]中的研究,若每个状态-动作对
1) 即时开销有界,|c(s, a)|≤C;
2) 学习率αt满足随机逼近条件
| $ \sum\limits_{t = 0}^{\infty} \alpha_{t} = \infty, \sum\limits_{t = 0}^{\infty} \alpha_{t}^{2}<\infty. $ | (10) |
我们的任务卸载模型符合条件1)。同时通过对学习率的设定,如设置αt=1/t,条件2)也可以得到满足。因此本文的任务卸载模型能够通过Q-learning方法收敛到最优解。基于Q-learning的在线任务卸载策略的流程见算法2。
算法2 基于Q-learning的任务卸载
步骤1) 设置t=1,初始化动作值函数
步骤2) 观测系统状态st,按照概率ε执行随机卸载决策;或按照(1-ε)的概率,执行卸载决策
步骤3) 观测系统开销c(st, at)以及新状态st+1;
步骤4) 存储经验值et=(st, at, c(st, at), st+1);
步骤5) 按照式(9)更新Qt(st, at);
步骤6) 设置t=t+1;
步骤7) 若t>T,算法结束;否则跳转步骤2)。
Q-learning是一个基于表格的策略,表格横轴为状态空间,纵轴为动作空间,表格内为所有状态-动作对的Q值。为达到收敛,表格中每一个数据都需要得到多次更新。但在算法2中,每个时隙只能更新表格中的一个数据,如果状态空间和动作空间非常大,将面临维度灾难并难以收敛。为应对这种情况,加快收敛速度,将采用基于拟合的方式,实现在单个时隙中批量更新Q值。
2.2.2 基于DQN的任务卸载为避免对每个
| $ Q(s, a ; \boldsymbol{\theta}) \approx Q^{*}(s, a), \forall s \in \mathcal{S}, a \in \mathcal{A}, $ | (11) |
其中:Q(s, a; θ)为深度神经网络的输出,θ为神经网络的参数,将深度神经网络与Q-learning的结合称为DQN[16]。
相比于Q-learning中每次只更新单个状态-动作对的动作值函数,DQN中每次网络参数θ的更新,使所有状态-动作对的动作值函数都能得到更新。同时,还将经验回放利用于神经网络的更新,加快DQN的收敛速度。首先设置容量为P的经验池
| $ L\left(\boldsymbol{\theta}_{t}\right) = \mathbb{E}_{{\mathop {\mathcal{P}}\limits^{○}} _{t} \sim U\left(\mathcal{p}_{t}\right)}\left[\left(y_{t}-Q\left(s_{t}, a_{t} ; \boldsymbol{\theta}_{t-1}\right)\right)^{2}\right], $ | (12) |
| $ y_{t} = c\left(s_{t}, a_{t}\right)+\gamma \min \limits_{a^{\prime}} Q\left(s_{t+1}, \boldsymbol{a}^{\prime} ; \boldsymbol{\theta}_{t-1}\right) . $ | (13) |
算法3 基于DQN的任务卸载
步骤1) 初始化神经网络参数θ0,设置t=1;
步骤2) 观测系统状态st,按照概率ε执行随机卸载决策;或按照(1-ε)的概率,执行卸载决策
步骤3) 观测系统开销c(st, at)及新状态st+1、经验值et=(st, at, c(st, at), st+1),更新经验池
步骤4) 从经验池
步骤5) 按照式(13)更新yt,在θ方向对损失函数执行梯度下降,更新θt;
步骤6) 设置t=t+1;
步骤7) 若t>T,算法结束;否则跳转步骤2)。
3 仿真实验 3.1 参数设置这一章节通过仿真实验验证本文的任务卸载策略。假设用户在4×4的正方形,共L=16个方格(位置)的网络中移动,网络场景大小为2 km×2 km。用户的移动模式参照文献[11]中的设置,用户以0.6的概率保持不移动,即
移动边缘计算网络的参数设定主要参照文献[17]。除位于场景中心的宏基站外,网络中还有N=20个帮助节点。本地节点的传输功率为20 dBm,到宏基站和其他帮助节点的路径损耗分别为(35.7+lgd+33.4) dB和(35.7+lgd+18.4) dB,d为本地节点到帮助节点的距离,单位为m。系统带宽为20 MHz,功率频谱密度为-174 dBm/Hz。本地节点和宏基站的处理速度分别为10和35 Mbps,其他帮助节点的处理速度均匀分布于(10, 40) Mbps。
在对DQN任务卸载策略进行仿真时,采用TensorFlow框架来搭建深度神经网络[18]。在神经网络中包含2层隐藏层,分别含有128和64个神经元,采用ReLU作为激活函数[19]。其他参数列在表 1中。
|
|
表 1 DQN参数设置 Table 1 DQN parameters |
这一节验证基于Q-learning和DQN的任务卸载策略的表现,并与最优卸载方案进行比较。由于在实际中系统信息难以获得,最优卸载方案无法应用,因此本文将最优任务卸载算法作为基准来验证其他2个算法的效果。
1) 收敛性:图 3通过展示动作值函数的累计平均值来验证基于Q-learning和DQN的任务卸载策略的收敛性。不失一般性地,选择系统状态s=(7, 30)和动作a=1的动作值函数作为示例,即Q((7, 30), 1)。

|
Download:
|
| 图 3 算法收敛性比较 Fig. 3 Convergence of the algorithms | |
从图 3可以看出,与基于Q-learning的卸载策略相比,基于DQN的算法能够更快速地收敛到接近最优解。正如在2.3.2节中的讨论,基于Q-learning的任务卸载算法只有在系统处于状态s=(7, 30)且执行a=1时,对应的动作值函数Q((7, 30), 1)才能够得到单次更新。而基于DQN的任务卸载算法,由于深度神经网络参数θ在每个时隙都进行更新,因此对于任意(s, a)∈ ×,动作值函数在每个时隙都能够得到更新。因此在DQN算法中Q((7, 30), 1)的更新次数远远多于Q-learning算法,基于DQN的任务卸载的收敛速度明显高于Q-learning的方法。
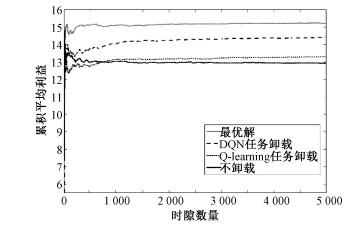
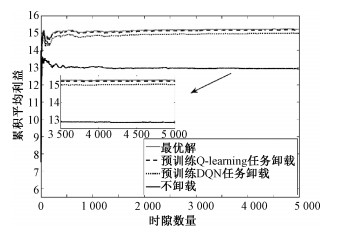
2) 近优性:在2.2.1节中提到,本文中的任务卸载模型采用的Q-learning算法能够以概率1收敛到最优解。为验证该结论,将通过长期任务的时延来验证算法的近优性。图 4和图 5的纵坐标为系统回报Rt,定义为Rt=C-c(st, at),C为开销的上界。
|
Download:
|
| 图 4 算法性能比较 Fig. 4 Performance of the algorithms | |
|
Download:
|
| 图 5 预训练后算法性能比较 Fig. 5 Performance of the algorithms after training | |
同样的,图中的最优解是基于系统信息已知的假设,因此只作为其他算法的表现基准,而基于Q-learning和DQN的任务卸载策略中,系统信息为后验知识,系统利用历史反馈以实现自主在线学习。同时,我们还将算法同“不卸载”进行比较,它忽略了用户的移动性,对所有任务都不执行任务卸载,只在本地节点进行处理。我们将观察不考虑用户移动性时的系统表现。
在图 4中,基于Q-learning和DQN的算法对系统信息没有先验知识,从时隙t=0开始在线学习。因此在仿真的前期时隙中,Q-learning由于学习数据的不足,导致算法对系统信息掌握较少,表现较差。此时基于Q-learning的任务卸载策略实现的系统回报,甚至低于不执行任务卸载的策略。但值得注意的是,基于Q-learning策略的回报始终保持着上升的趋势,并且从第800个时隙开始,表现超过不执行任务卸载的策略,且一直维持着上升的趋势。而基于DQN的任务卸载有着明显的优势,不论是仿真前期还是后期,获得的利益始终高于Q-learning和不执行卸载的策略,同时也维持着最为明显的系统回报上升的趋势。在短时间内,不考虑用户移动性的策略表现似乎与提出的算法相差不多,但从长时间尺度来看,考虑移动性的任务卸载策略,在后期表现更为优异。下面将进一步展示算法对长期任务的表现。
图 5将经过预训练的Q-learning和DQN的算法与最优解进行比较,从而验证2个算法的近优性。其中基于Q-learning和DQN的任务卸载分别经过200 000和2 000个时隙的预训练,已经接近收敛。从时隙t=0开始进行在线的任务卸载。可以看出,与图 4的未经预训练相比,2个算法经过预先学习后已经对系统掌握大量信息,Q-learning的表现已经非常接近最优解,证明它的确能够在系统信息未知的情况下,通过在线学习达到接近最优解,并高效地完成任务卸载。而DQN的表现虽然略逊于Q-learning,但相差不大。然而值得注意的是,相比于Q-learning,基于DQN的任务卸载只需要1 % 的预训练时间就能够达到接近Q-learning的效果,这也再一次验证了基于DQN的任务卸载策略快速的收敛速度。可以看出,在长期任务中,提出的算法在表现上一直明显优于不考虑用户移动性的不卸载策略,这也验证了上一段的讨论,考虑用户的移动性在长时间尺度上可以实现更高的系统利益。
4 结束语本文研究MEC网络中高效的在线任务卸载策略。为最小化移动用户在系统中的长期任务时延,利用马尔科夫决策过程建立任务卸载模型。在假设系统信息已知的前提下,提供了系统的最优解。在系统信息未知时,提出2个在线学习的算法,基于Q-learning和DQN的任务卸载。其中基于Q-learning的任务卸载在本文的模型中能够收敛到最优解,而基于DQN的算法能够快速收敛,并且达到接近最优解的表现。
| [1] |
Li Y T, Cheng Q F, Liu X M, et al. A secure anonymous identity-based scheme in new authentication architecture for mobile edge computing[J]. IEEE Systems Journal, 2021. Doi:10.1109/JSYST.2020.2979006 |
| [2] |
Dinh T Q, Tang J H, La Q D, et al. Offloading in mobile edge computing: task allocation and computational frequency scaling[J]. IEEE Transactions on Communications, 2017, 65(8): 3571-3584. Doi:10.1109/TCOMM.2017.2699660 |
| [3] |
Mao Y Y, You C S, Zhang J, et al. A survey on mobile edge computing: the communication perspective[J]. IEEE Communications Surveys & Tutorials, 2017, 19(4): 2322-2358. Doi:10.1109/COMST.2017.2745201 |
| [4] |
Mach P, Becvar Z. Mobile edge computing: a survey on architecture and computation offloading[J]. IEEE Communications Surveys & Tutorials, 2017, 19(3): 1628-1656. Doi:10.1109/COMST.2017.26823 |
| [5] |
You C S, Huang K B, Chae H, et al. Energy-efficient resource allocation for mobile-edge computation offloading[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1397-1411. Doi:10.1109/TWC.2016.2633522 |
| [6] |
Mao Y Y, Zhang J, Song S H, et al. Stochastic joint radio and computational resource management for multi-user mobile-edge computing systems[J]. IEEE Transactions on Wireless Communications, 2017, 16(9): 5994-6009. Doi:10.1109/TWC.2017.2717986 |
| [7] |
Chen X F, Zhang H G, Wu C, et al. Optimized computation offloading performance in virtual edge computing systems via deep reinforcement learning[J]. IEEE Internet of Things Journal, 2019, 6(3): 4005-4018. Doi:10.1109/JIOT.2018.2876279 |
| [8] |
Min M H, Xiao L, Chen Y, et al. Learning-based computation offloading for IoT devices with energy harvesting[J]. IEEE Transactions on Vehicular Technology, 2019, 68(2): 1930-1941. Doi:10.1109/TVT.2018.2890685 |
| [9] |
Huang L, Bi S Z, Zhang Y J A. Deep reinforcement learning for online computation offloading in wireless powered mobile-edge computing networks[J]. IEEE Transactions on Mobile Computing, 2020, 19(11): 2581-2593. Doi:10.1109/TMC.2019.2928811 |
| [10] |
余翀, 邱其文. 基于栅格地图的分层式机器人路径规划算法[J]. 中国科学院大学学报, 2013, 30(4): 528-538, 546. Doi:10.7523/j.issn.2095-6134.2013.04.015 |
| [11] |
Cheung M H, Huang J W. DAWN: delay-aware Wi-Fi offloading and network selection[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(6): 1214-1223. Doi:10.1109/JSAC.2015.2416989 |
| [12] |
Nicholson A J, Noble B D. BreadCrumbs: forecasting mobile connectivity[C]//MobiCom ′08: Proceedings of the 14th ACM International Conference on Mobile Computing and Networking. 2008: 46-57. DOI: 10.1145/1409944.1409952.
|
| [13] |
Gambs S, Killijian M O, del Prado Cortez M N. Next place prediction using mobility Markov chains[C]//MPM ′12: Proceedings of the First Workshop on Measurement, Privacy, and Mobility. 2012: 1-6. DOI: 10.1145/2181196.2181199.
|
| [14] |
Sutton R S, Barto A G. Reinforcement learning: an introduction[M]. 2nd ed.Cambridge, MA: The MIT Press, 2018.
|
| [15] |
Watkins C J C H, Dayan P. Q-learning[J]. Machine Learning, 1992, 8(3/4): 279-292. Doi:10.1007/BF00992698 |
| [16] |
Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533. Doi:10.1038/nature14236 |
| [17] |
Zhu Z W, Jin S D, Yang Y, et al. Time reusing in D2D-enabled cooperative networks[J]. IEEE Transactions on Wireless Communications, 2018, 17(5): 3185-3200. Doi:10.1109/twc.2018.2808259 |
| [18] |
Abadi M, Barham P, Chen J M, et al. Tensorflow: a system for large-scale machine learning[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2016, abs/1605.08695.
|
| [19] |
Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks[C]//Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. 2011: 315-323.
|
 2022, Vol. 39
2022, Vol. 39 


