2. 中国科学院上海微系统与信息技术研究所, 上海 200050;
3. 中国科学院大学, 北京 100049
2. Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 200050, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
异构网络的快速发展在各类无线网络应用中发挥中极其重要的作用,例如,物联网、车联网、智慧工厂等。而为了应对正在快速增长的无线数据量的需求,无线网络密集化,即密集组网被认为是下一代无线网络发展的必然趋势之一[1]。各种类型小型基站,例如,微基站、皮基站、飞基站的密集布置对于扩大小区的覆盖范围以及增强用户基站之间链接的通信质量大有裨益,而相比较于只有宏基站部署的解决方案,各种小型基站的密集部署也有利于不同区域的频谱复用。
但是无线网络的密集化往往会导致严重的网络频繁切换的问题,有时也被称之为网络的乒乓效应,其会严重影响到网络性能,这也是目前密集无线网络面临的主要挑战之一。
为解决这一问题,近年来已有的很多研究工作把目光集中在自组织网络(self-organizing network, SON)中,并且这也是最早在3GPP Rel-8标准中提出的解决方案。
Lee和Cho[2]提出一个用户集体网络切换的解决方案,该方案通过优化用户接入初期阶段的延迟来降低网络中断的概率。Fischionei等[3]提出混合型的系统模型来优化用户接入,并且该项工作同时考虑了用户的移动速度以及用户的距离造成的影响。文献[4]提出一个马尔科夫分析模型,利用特定的场景参数,例如路径损耗参数、用户移动速度,以及小区负载等等,最终得到依场景变化的最优网络切换解决方案。Ye等[5]提出一个分布式负载感知的用户接入算法,该算法复杂度低且考虑了负载均衡以及用户接入过程中涉及的频谱划分等因素。文献[6]从降低能量消耗的角度出发,优化在用户接入过程中的频谱分配及功率分配。孟庆民等[7]提出一种基于马尔科夫链预测的切换方案,在触发网络切换时会预测下一个基站的相关状态信息。
但是以上的这些工作其实都很少考虑用户频繁切换网络的这个问题。在相关的参考文献当中,想尝试解决该问题更多地还是依赖于机器学习的方法。例如文献[8]借助于深度强化学习训练得到一个最优的系统控制器,该控制器可以用来降低网络切换的次数同时也保障了网络的吞吐量性能。目前为止和本文工作最相关的是文献[9],在该项工作当中,作者首次论述建立无线网络切换过程和多臂老虎机模型之间的等价性,除此以外该文献也提出一种改进的置信区间上界(upper-confidence bound, UCB)策略以较低复杂度来解决用户接入频繁切换的问题。
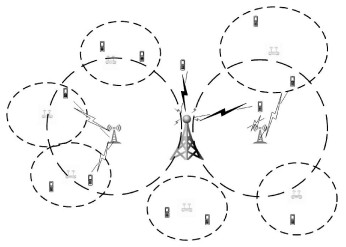
1 系统模型 1.1 网络模型考虑一个区域范围内的无线密集网络,如图 1所示,该区域内部署了前文所述的各类型基站: 宏基站、微基站、皮基站、飞基站。这些基站的集合表示为
| $ B=\{1,2, \cdots, N\}, $ | (1) |
|
Download:
|
| 图 1 无线密集网络示意图 Fig. 1 Wireless dense network | |
其中N为基站总数目。用户的集合表示为
| $ U=\{1,2, \cdots, K\}, $ | (2) |
所有这些基站都可以为其覆盖范围内的用户提供无线服务。
为描述简洁,本文假设时间尺度划分为均等长度的时隙。在传统的无线网络系统中,用户接入与切换往往是由配备在基站端的控制器来决定的。但是很多研究已经表明在下一代无线网络系统中,由于网络的高度异构性,网络用户主导的接入方案正成为主流的趋势[1, 10],这也是本文中所考虑的用户接入机制模型。
对于某一个特定的网络用户,记该用户在时隙t所选择建立链接的基站为at∈B。那么在总时间长度T范围内的用户接入模式可以表示为
| $ \varTheta=\left(a_{1}, a_{2}, \cdots, a_{T}\right). $ | (3) |
本文并不考虑其他复杂的接入模式,例如,3GPP Rel-12中的双连接,即一个用户可以同时接入2个不同的基站接受服务。
用户在时隙t结束后会立即收到奖励u(t, at)。在本文中,我们旨在建立适用于用户接入模型的通用框架和解决思路,故在此并不指定这里奖励的具体指标。在实际的系统当中,这里的奖励通常刻画的是某项网络性能指标的优化,例如,最大化数据吞吐量、最小化网络时延,或者是最小化用户能量消耗等。
假设奖励由一个随机变量产生,出于理论分析的方便,这里将奖励归一化至0~1。每一个基站都有各自的随机变量,其数学期望表达为
| $ u_{i}=E[u(t, i)], i=1, \cdots, N, $ | (4) |
为方便表达同时也不失一般性,令这里的N个数学期望是依升序排列
| $ u_{1} \leqslant u_{2} \leqslant \cdots \leqslant u_{N}, $ | (5) |
同时记它们之间的均值差距为
| $ \varDelta_{i}:=u_{N}-u_{i}, i=1, \cdots, N-1, $ | (6) |
从时隙1开始计时至时隙T为止,该用户所接受到的总奖励可以表示为
| $ A(\varTheta)=\sum\limits_{t=1}^{T} u\left(t, a_{t}\right), $ | (7) |
用户的目标是在缺乏关于可向其提供无线服务的这N个基站的准确统计信息情况下最大化其可以获得的总奖励量。而为了实现这一优化目标,用户需要在尽可能短的时间内分辨出有最高数学期望奖励的那个最优基站。而想要做到这一点就需要对每个基站进行足够的接入尝试,以对其分布做足够的采样估计。在实际系统中,若以最大化奖励为目标,则用户所采用的决策就必须平衡好“探索”与“利用”之间的均衡。一方面,用户为了增加眼前的奖励,决策应偏向尽可能“利用”经验最佳基站;另一方面,如果是从长远角度考虑,用户需要更多地“探索”其他基站以找到可能潜在的性能更佳的基站。为平衡这种关系,一种流行的方法在统计学以及机器学习领域内广泛使用,该方法是将“探索”与“开发”困境建模为多臂老虎机问题[11]。
解决多臂老虎机问题的经典算法为置信上界算法[12]。该方法为多臂老虎机的N个操纵杆维护它们各自的置信上界
| $ \hat{u}_{i}+\sqrt{\frac{2 \log t}{T_{i}}}, $ | (8) |
其中:
用户在每一个时隙开始时做出决策决定其在该时隙内选择建立链接的基站。我们称用户触发了一次网络切换为用户在相邻的2个时隙选择了不同的基站接入。用户触发一次网络切换会造成一些额外的损失,例如,时延、能量消耗或者是额外的频谱资源开销用来发送网络切换的控制信号。所以,频繁的网络切换很可能会严重降低服务质量(quality of service, QoS)以及体验质量(quality of experience, QoE)。与文献[8]及文献[10]类似,假设每一次切换会导致固定的损失C,那么在使用给定算法Π情况下,截止到时隙T为止,用户的网络切换损失可以表达为
| $ H^{\varPi}(\varTheta)=C \sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T} 1_{a_{t}=i, a_{t-1} \neq i}, $ | (9) |
这里1S表示事件S的指示函数。
由此可见,虽然多臂老虎机模型很好地刻画了“探索”与“利用”之间的均衡问题,但是这种方法无法直接运用于用户接入问题,因为该算法需要在各个基站之间反复切换。而该问题在无线网络中会尤其严重。考虑如下场景,当拥有最高数学期望奖励的2个基站之间的数学期望差距ΔN-1非常小的时候,该算法很难区分哪一个才是最好的,从而陷入在二者之间反复切换的僵局。为克服这一问题,在文献[13]中,算法设置在运行足够长的时间后终止探索过程,进而选择任意一个足够好的基站一直建立链接。
1.2 在线学习中的后悔值与切换次数上界为评价以置信上界算法等为代表的在线学习算法的性能优劣,常用的性能指标为后悔度。该指标定义为截止到T时所获得的总奖励与一直采用最高奖励均值的决策之间的差值。通常在理论分析时,关注的是后悔度的数学期望
| $ R^{\varPi}(T)=E\left[T \cdot u_{N}-\sum\limits_{t=1}^{T} u\left(t, a_{t}\right)\right]. $ | (10) |
Auer等[12]的早期工作已经表明传统置信上界算法的期望后悔度有严格上界:O(logT),这意味着该算法的后悔值是时隙T的高阶无穷小量,但同时文献也指出该算法运行时在不同操作杆之间切换次数的数学期望上界也是O(logT)。而这就意味着在无线密集网络问题中,由于网络切换带来的损失不可忽略,置信上界算法无法直接运用。
Shen和Schaar[9]提出一种直接的改进置信上界算法并给出了理论分析。在该算法中,连续的k个时隙会被组合在一起成为一个大时隙,并且k会从1开始逐一增加。在这连续的k个时隙内,用户只在第一个时隙开始时做出决策选择基站并一直与该基站保持接入。作者证明了在该策略下,其依旧能保证以O(logT) 为上界的期望后悔度,但用户在不同基站之间切换次数的数学期望上界可以降低为:o(logT)。这样一来就可以保证用户在不同基站之间切换造成的损失在阶数上可以忽略不计。
2 高效的用户接入策略本节首先提出基于操作杆淘汰机制的一种用户接入算法。随后的理论分析可以表明,该算法在保持期望后悔度上界O(logT) 不变的情况下,可以将用户在不同基站之间切换次数的数学期望上界降低为常数阶。相比较于前文提到的算法有重要改进。
2.1 基于淘汰机制的用户接入算法本节提出的算法以回合的形式来运行。每个回合包含若干连续个时隙。在算法运行过程中需要引入一个监控变量
每个回合的均等采样步骤所需要的时隙总数由当前所剩余的候选基站总数和当前的回合数所决定。用户在该步骤对每个基站保持接入连续的Lm个时隙
| $ L_{m}=n_{m}-n_{m-1}, $ | (11) |
其中nm的定义如下
| $ n_{m}:=\frac{2 \log \left(C T \hat{\varDelta}{}_{m}^{2}\right)}{\hat{\varDelta}{}_{m}^{2}}. $ | (12) |
用户在完成上述步骤之后会用其所获得的奖励数据来更新参数,包括均值的更新、监控变量的更新和采样次数的更新。
每个回合的最后阶段,用户会根据更新后的系统参数来淘汰掉被分类判断为次优的基站,也就是说在这之后的所有回合用户都不会再选择这个基站接入。这里设置淘汰判决条件为
| $ \hat{u}_{i}+\sqrt{\frac{\log \left(C T \hat{\varDelta}{}_{m}^{2}\right)}{2 n_{m}}}<\max \limits_{j \in B_{m}}\left\{\hat{u}_{j}-\sqrt{\frac{\log \left(C T \hat{\varDelta}{}_{m}^{2}\right)}{2 n_{m}}}\right\}, $ | (13) |
其中Bm为当前回合m尚未被淘汰的基站集合。在该回合之后所有满足上述判决条件的基站i都会被淘汰。
完整算法的具体流程见算法1。
算法1 UAAE(user association with arm-elimination)用户接入算法:
步骤1) 接受输入时间长度T,切换损失C,初始化监控变量等
步骤2) 若|Bm|=1,则用户保持接入Bm中的唯一基站直到时隙T,否则执行步骤3)。
步骤3) 均等采样:依次选择接入|Bm|中的基站,并且每个基站保持接入Lm个时隙,计算从每个基站i获得的总奖励
| $ r_{i}=\sum\limits_{t^{\prime}=t}^{t+L_{m}{\left|B_{m}\right|-1}} u\left(t^{\prime}, {i}\right), $ | (14) |
步骤4) 参数更新:按以上得到数据更新如下系统参数
| $ \hat{u}_{i}=\hat{u}_{i}+\frac{1}{n_{m}}\left(r_{i}-L_{m} \hat{u}_{i}\right), $ | (15) |
| $ t=t+L_{m}\left|B_{m}\right|, $ | (16) |
| $ \hat{\varDelta}_{m+1}=\frac{\hat{\varDelta}_{m}}{2}, $ | (17) |
步骤5) 操作杆淘汰:按照新的系统参数以及淘汰判决条件(13)更新Bm,
| $ m=m+1, $ | (18) |
步骤6) 若t>T,算法结束,否则跳转返回至步骤2)。其中,|S|表示集合S的势。
2.2 理论分析定理1 算法1保持了和置信上界相同的后悔度数学期望上界,同时用户在不同基站之间切换次数的数学期望上界可以降低为常数阶:
a) 算法1可以保证如下后悔度的上界
| $ R(T) \leqslant \sum\limits_{i=1}^{N-1}\left(\varDelta_{i}+\frac{32 \log \left(C T \varDelta_{i}^{2}\right)}{\varDelta_{i}}+\frac{96}{C \varDelta_{i}}\right), $ | (19) |
b) 对于每一个次优基站i,设置变量mi为第一次满足如下条件的回合数:
| $ m_{i}=\min \left\{m \mid \hat{\varDelta}_{m}<\varDelta_{i}\right\}, $ | (20) |
算法1可以保证如下切换次数的上界
| $ \begin{gathered} E[H(\Theta)] \leqslant \sum\limits_{j=0}^{m_{N-1}} \frac{(N-1) b^{2}}{C \hat{\varDelta}{}_{j}^{2} \log \left(C b^{2}\right)}+ \\ \sum\limits_{i=1}^{N-1}\left((N-i+1)\left(m_{i}-m_{i-1}\right)+\frac{b^{2}}{C \hat{\varDelta}{}_{m_{i}}^{2} \log \left(C b^{2}\right)}\right), \end{gathered} $ | (21) |
证明 为描述简洁,首先需要定义3个事件:E1,E2,E3。
1) E1:每一个次优基站i都会在第mi+1回合之前满足淘汰判决条件,从而被淘汰掉不再被使用;
2) E2:存在某一个次优基站i没有在第mi+1回合之前满足淘汰判决条件,被继续使用;
3) E3:最优基站被错误淘汰。
这里需要注意,以上事件分解得到的3个子集的并集是事件全集,但是交集未必是空集。
当事件E1发生时,每一个次优基站i都只能提供接入至多mi回合。在所有的次优基站都被淘汰掉以后,网络用户便不会再触发网络切换,由此可以得到在该事件发生的情况下用户触发网络切换次数的上界
| $ F_{1}=\sum\limits_{i=1}^{N-1}(N-i+1)\left(m_{i}-m_{i-1}\right), $ | (22) |
其中m0=0。
相应地,由于每一个次优基站i被选择接入的次数都不超过nmi。结合Δi并且通过不等式放缩,可以得到当事件E1发生时,所造成的后悔度
| $ \begin{aligned} &\sum\limits_{i=1}^{N-1} \varDelta_{i} n_{m_{i}}=\sum\limits_{i=1}^{N-1} \varDelta_{i} \frac{2 \log \left(C T \hat{\varDelta}_{m}^{2}\right)}{\hat{\varDelta}{}_{m}^{2}} \\ &\leqslant \sum\limits_{i=1}^{N-1}\left(\varDelta_{i}+\frac{32 \log \left(C T \varDelta_{i}^{2}\right)}{\varDelta_{i}}\right), \end{aligned} $ | (23) |
当事件E2发生时,由文献[14]可以得知某一个次优基站i没有在第mi+1回合之前满足淘汰判决条件的发生概率有上界:
| $ \begin{gathered} \frac{2}{C T \hat{\varDelta}{}_{m_{i}}^{2}} \times \frac{T b^{2}}{2 \log \left(C T b^{2}\right)}=\frac{b^{2}}{C \hat{\varDelta}{}_{m_{i}}^{2} \log \left(C T b^{2}\right)}\\ <\frac{b^{2}}{C \hat{\varDelta}{}_{m_{i}}^{2} \log \left(C b^{2}\right)}, \end{gathered} $ | (24) |
这里利用用户最大可能触发的网络切换次数
| $ D_{\max }=\frac{T}{\frac{2 \log \left(C T \hat{\varDelta}{}_{0}^{2}\right)}{\hat{\varDelta}{}_{0}^{2}}} \leqslant \frac{T b^{2}}{2 \log \left(C T b^{2}\right)}. $ | (25) |
上式成立的条件也是基于事实在均等采样步骤中每个基站保持接入Lm个时隙,而Lm是单调递增的。对所有N-1个次优基站求和,可以得到针对事件E2的用户触发网络切换次数的上界
| $ F_{2}=\sum\limits_{i=1}^{N-1} \frac{b^{2}}{C \hat{\varDelta}{}_{m_{i}}^{2} \log \left(C b^{2}\right)}. $ | (26) |
相应地,当事件E2发生时,其造成的后悔度可以如下表达:
| $ \sum\limits_{i=1}^{N-1} \varDelta_{i} \frac{2}{C T \hat{\varDelta}{}_{m_{i}}^{2}} T \leqslant \sum\limits_{i=1}^{N-1} \frac{8}{C \hat{\varDelta}{}_{m_{i}}^{2}} \leqslant \sum\limits_{i=1}^{N-1} \frac{32}{C \varDelta_{i}}. $ | (27) |
当事件E3发生时,同样可以由文献[14]得知最优基站被某一个次优基站i所错误淘汰的概率也有上界
| $ \begin{gathered} F_{3}=\sum\limits_{j=0}^{m_{N-1}}(N-1) \frac{2}{C T \hat{\varDelta}{}_{j}^{2}} \frac{T b^{2}}{2 \log \left(C T b^{2}\right)} \\ <\sum\limits_{j=0}^{m_{N-1}} \frac{(N-1) b^{2}}{C \hat{\varDelta}{}_{j}^{2} \log \left(C b^{2}\right)}, \end{gathered} $ | (28) |
注意该求和上下限为从0到mN-1回合,这是因为最优基站在mN-1回合之后被淘汰的情况实际上已经被包含在了事件E2当中。
相应地,当事件E3发生时,记最优基站在m*回合被淘汰,那么最优基站被淘汰后的每一个时隙都会增加后悔值。这里可以将该情况下的后悔值做如下不等式放缩:
| $ \begin{gathered} \sum\limits_{m_{*}=0 i,}^{m_{N-1}}\sum\limits_{ m_{i \geqslant} m_{*}} \frac{2}{C T \hat{\varDelta}{}_{m_{*}}^{2}} T \max _{j, m_{j} \geq_{m_*}} \varDelta_{j}\\ \leqslant \sum\limits_{m_{*}=0 i, }^{m_{N-1}} \sum\limits_{m_{i} \geq{m_*}} \frac{2}{C \hat{\varDelta}{}_{m_{*}}^{2}} 4 \hat{\varDelta}_{m_{*}}\\ =\sum\limits_{i=1}^{N-1} \sum\limits_{m_{*}=0}^{m_{i}} \frac{8}{C 2^{-m_{*}}} \leqslant \sum\limits_{i=1}^{N-1} \frac{64}{C \varDelta_{i}} . \end{gathered} $ | (29) |
结合以上事件分解后的分部结论相加,可以得到定理1中的结论。
证明完毕。
在该算法中,用户对每个基站保持接入连续的Lm个时隙,而Lm可以被验证是指数增长的。文献[9]中的算法是逐一增长的。这样做的好处是更有利于减缓前文中已经提到的当拥有最高数学期望奖励的2个基站之间的数学期望差距ΔN-1非常小的时候,算法会很难区分这两者的问题。而从另一方面来说,非常小的ΔN-1也保证了即使用户需要在较长的连续时隙内选择次优的那个基站接入,也不会造成特别大的后悔度。
Lm同时也会随着T的增加而增加。这个设计能够保证如果总时间足够长,算法会在每个回合执行淘汰机制之前对当前回合还存在的基站做充分的估计。同时由于总时间足够长,在所有次优基站被淘汰前对它们进行采样所使用的时隙造成的后悔度也相对影响较小。
该算法所保障的低切换的特性为更实际的网络模型提供了很好的使用条件。在实际的网络环境中,网络的各方面性能往往是动态变化的,即前文中所假设的奖励值由一个稳定分布所产生的条件不再成立。而算法往往需要在环境发生变化时重新开始学习以适应新的网络环境。这样一来,如果使用常规的多臂老虎机算法,则不可避免地重新造成了大量的网络切换。所以,在动态环境下,当用户需要重新开始学习过程时,UAAE算法能够保证节省大量的切换次数。
3 实验结果分析本节将利用蒙特卡洛仿真的方法验证本文所提算法的有效性。所有结果均为500次仿真实验的平均结果。
参数设定如下,系统中总共包含30个基站。每一个基站的期望奖励值由正态分布产生,N(5, δ2)。基站i在每次被用户选中接入时产生的奖励同样服从正态分布N(ui, 1)。这样设定的好处是可以通过控制方差δ来调节不同基站之间的优劣差距。δ越小意味着△i也越小。仿真的总时间长度为T=5×105,监控变量初始值为b=1,用户每次网络切换的损失为C=1。
为对比本文提出算法的有效性,本文选择如下算法作为对比算法:
a) 置信上界算法;
b) 改进置信上界算法[9];
c)
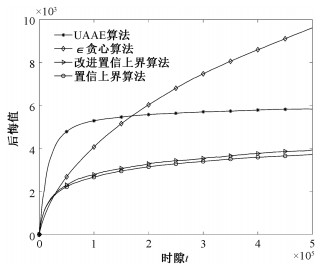
首先验证4种不同算法的后悔值性能表现。如图 2所示,可以清晰地看出,除
|
Download:
|
| 图 2 不同算法下的后悔值性能指标对比 Fig. 2 Cumulative regrets with various bandit handover algorithms | |
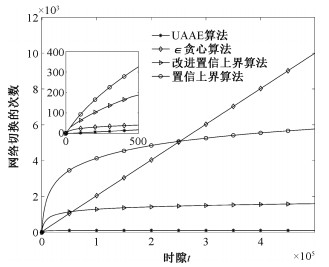
图 3表现的是4种算法下用户所触发的网络切换次数随时隙的变化曲线对比。UAAE算法相较于其他3个算法有着绝对的优势。这其中的原因正如前文所解释,用户最终淘汰掉N-1个基站,从而不会再触发任何网络切换。
|
Download:
|
| 图 3 不同算法下的用户触发网络切换次数对比 Fig. 3 Cumulative numbers of handovers with various bandit handover algorithms | |
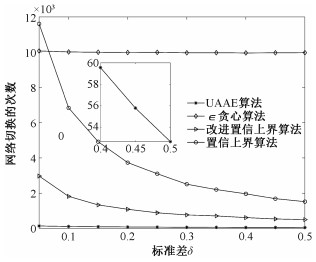
接下来验证不同基站之间的期望奖励差距大小对算法性能的影响及敏感度分析。针对这点的研究是必要的,但是往往被很多使用多臂老虎机模型的研究工作所忽略。不同于其他可以使用多臂老虎机的应用系统(例如推荐系统等)。在实际无线网络系统中,用户所能选择接入的基站往往可能不会有太大的性能差距。这就给很多多臂老虎机算法带来了挑战。在该实验中,参数δ变化范围0.05~0.5。从图 4可以看出,
|
Download:
|
| 图 4 不同算法对于基站间差距大小的敏感度对比 Fig. 4 Sensitivity to the gaps between the SBSs | |
本文利用多臂老虎机模型提出一个低复杂度的无线网络用户接入算法。通过3组不同角度的对比试验,验证了本文所提算法的有效性、鲁棒性,为下一代无线通信网络中用户接入系统设计提供一种解决思路。该算法除了有效降低用户触发网络切换的次数,也保证其后悔值性能不会受到影响。
本文主要考虑的是稳定环境下的解决方案,即基站产生奖励值的概率分布是恒定不变的。但是正如前文的讨论中所指出,当用户面临动态变化的网络环境时,其需要频繁重新开始学习过程。而本文所提算法为在动态环境下的部署使用提供了很好的基础。
| [1] |
Boccardi F, Heath R W, Lozano A, et al. Five disruptive technology directions for 5G[J]. IEEE Communications Magazine, 1996, 52(2): 74-80. Doi:10.1109/MCOM.2014.6736746 |
| [2] |
Lee W, Cho D H. Enhanced group handover scheme in multiaccess networks[J]. IEEE Transactions on Vehicular Technology, 2011, 60(5): 2389-2395. Doi:10.1109/TVT.2011.2140386 |
| [3] |
Fischione C, Athanasiou G, Santucci F. Dynamic optimization of generalized least squares handover algorithms[J]. IEEE Transactions on Wireless Communications, 2014, 13(3): 1235-1249. Doi:10.1109/TWC.2014.013014.121720 |
| [4] |
Guidolin F, Pappalardo I, Zanella A, et al. Context-aware handover policies in HetNets[J]. IEEE Transactions on Wireless Communications, 2016, 15(3): 1895-1906. Doi:10.1109/TWC.2015.2496958 |
| [5] |
Ye Q Y, Rong B Y, Chen Y D, et al. User association for load balancing in heterogeneous cellular networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(6): 2706-2716. Doi:10.1109/TWC.2013.040413.120676 |
| [6] |
Videv S, Haas H. Energy-efficient scheduling and bandwidth- energy efficiency trade-off with low load[C]//2011 IEEE International Conference on Communications(ICC). June 5-9, 2011, Kyoto, Japan. IEEE, 2011: 1-5. DOI: 10.1109/icc.2011.5962571.
|
| [7] |
孟庆民, 赵媛媛, 岳文静, 等. 动态超密集网络中的Markov预测切换[J]. 通信学报, 2018, 39(10): 166-174. Doi:10.11959/j.issn.1000-436x.2018225 |
| [8] |
Wang Z, Li L H, Xu Y, et al. Handover control in wireless systems via asynchronous multiuser deep reinforcement learning[J]. IEEE Internet of Things Journal, 2018, 5(6): 4296-4307. Doi:10.1109/jiot.2018.2848295 |
| [9] |
Shen C, van der Schaar M. A learning approach to frequent handover mitigations in 3GPP mobility protocols[C]//2017 IEEE Wireless Communications and Networking Conference. March 19-22, 2017, San Francisco, CA, USA. IEEE, 2017: 1-6. DOI: 10.1109/WCNC.2017.7925950.
|
| [10] |
Zhou Y M, Shen C, van der Schaar M. A non-stationary online learning approach to mobility management[J]. IEEE Transactions on Wireless Communications, 2019, 18(2): 1434-1446. Doi:10.1109/TWC.2019.2893168 |
| [11] |
Bubeck S. Regret analysis of stochastic and nonstochastic multi-armed bandit problems[M]. Boston: Now Publishers Inc, 2012. Doi:10.1561/9781601986276
|
| [12] |
Auer P, Cesa-Bianchi N, Fischer P. Finite-time analysis of the multiarmed bandit problem[J]. Machine Learning, 2002, 47: 235-256. Doi:10.1023/A:1013689704352 |
| [13] |
Sun Y X, Zhou S, Xu J. EMM: energy-aware mobility management for mobile edge computing in ultra dense networks[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(11): 2637-2646. Doi:10.1109/JSAC.2017.2760160 |
| [14] |
Auer P, Ortner R. UCB revisited: improved regret bounds for the stochastic multi-armed bandit problem[J]. Periodica Mathematica Hungarica, 2010, 61(1/2): 55-65. Doi:10.1007/S10998-010-3055.6 |
 2022, Vol. 39
2022, Vol. 39 


