随着多智体系统的发展,分布式优化算法受到广泛的重视并应用于诸多领域,如资源调度[1]、分布式传感器系统参数估计[2]、协同控制[3]及对分布式增强学习[4]等问题的相关研究。现存的分布式算法大多以各个节点目标函数梯度作为下降方向,以渐进收敛的方式达成最优共识状态,如分布式次梯度算法[5]、EXTRA[6]、DIGing[7]等。此类算法需要足够多迭代算法才能收敛到共识状态。另一类算法则以有限次迭代达成共识的FTC算法[8]为基础,在一个迭代周期内所有节点达到共识,如FADO[9]、FTC-NM[10]。其中FADO算法结合FTC与次梯度算法,因次梯度算法仅使用了函数基本的一阶信息,算法不能得到理想的收敛速率。FTC-NM算法利用二阶信息达到局部二次收敛速率。虽然收敛速率理想但需要传输二阶导数矩阵不适用于通信受限的场景中。考虑通信量与收敛速率的折中,本文中提出一种FTC算法与重球法相结合的分布式一阶算法。
本文贡献如下:提出基于FTC的分布式一阶加速优化算法。给出收敛性分析及算法参数的选取范围。证明本文算法与集中式重球法算法相同的收敛阶数。最后通过在随机生成的大规模网络上求解机器学习问题并与多种算法进行对比以体现算法的优良性能。
符号说明 本文中使用
假设网络中共有N个节点,每个节点有自己的目标函数fi(x)。在分布式协同优化中考虑如下问题
| $ \mathop {\min }\limits_{x \in {\mathbb{R}^d}} F(\boldsymbol{x}):=\frac{1}{N} \sum\limits_{i=1}^{N} f_{i}(\boldsymbol{x}), $ | (1) |
通过变量复制,问题(1)可以等价为如下问题
| $ \begin{array}{cc} \mathop {\min }\limits_{x \in {\mathbb{R}^{Nd}}} & \frac{1}{N} \sum\limits_{i=1}^{N} f_{i}\left(\boldsymbol{x}_{i}\right), \\ \text { s. t. } & \boldsymbol{x}_{1}=\cdots=\boldsymbol{x}_{N} . \end{array} $ | (2) |
此处x为x1, …, xN堆叠成的向量。等价问题(2)在分布式系统中被广泛应用,由于通信受限,并非所有节点都可以实时保持变量值相同,所以考虑每个节点i拥有自己的变量xi。为了分析算法的收敛速率引入以下描述函数性质的假设。
假设1(Li-光滑函数)假设函数fi(x)为Li-光滑,则函数fi(x)满足如下性质,即对任意x, y∈dom(fi),如下关系成立
| $ f_{i}(\boldsymbol{y}) \leqslant f_{i}(\boldsymbol{x})+\left\langle\nabla f_{i}(\boldsymbol{x}), \boldsymbol{y}-\boldsymbol{x}\right\rangle+\frac{L_{i}}{2}\|\boldsymbol{y}-\boldsymbol{x}\|^{2} $ |
Li-光滑的定义等价于函数fi的一阶导数Li-Lipschitz连续,是对函数变化程度的一种约束。
假设2(ν-限制性强凸函数)假设函数F(x)为ν-限制性强凸,则函数F(x)满足如下性质,对
| $ F(\boldsymbol{x})-\min F \geqslant \nu\left\|\boldsymbol{x}-\boldsymbol{x}^{*}\right\|^{2}, $ |
ν-限制性强凸是比强凸更弱的条件。
假设3(强制函数)函数fi(x)为强制函数,则当
对目标函数的假设会用于收敛性分析,为保证各个节点达成共识,需要对网络进行如下常见假设
假设4(网络连通)网络中的每一个节点至少存在一条到其他任意节点的路径。
只有在连通的网络中各个节点才能通过通信获取网络中的相关信息并进行协同。
假设5加权矩阵W为行随机矩阵而且当(i, j)∈ε时wij>0,其他情况下wij=0,且W1=1。
常见的W如
不失一般性,本节考虑
| $ \boldsymbol{x}_{i}^{t+1}=\sum\limits_{j \in \mathcal{N}_{i}} w_{i j} \boldsymbol{x}_{j}^{t}, \forall i \in \mathcal{V}, $ | (3) |
其中W是满足假设5的加权矩阵。当满足假设4,假设5时,通过式(3)所有节点的状态xit将渐进收敛于
| $ \mathop {\lim }\limits_{t \to \infty } {{\boldsymbol{x}}^{t}}=\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^0}, $ |
此处
Sundaram和Hadjicostis[8]通过单边z变换及Jordan分解证明FTC算法可以通过有限次迭代(3)达到x0并定义了相对节点的最小多项式。
定义1(节点i的最小多项式[8])qi(t)是多项式次数最低且满足eiTqi(W)=0T的首一多项式。其中W为满足假设5的加权矩阵。
节点i只需要Di≤N次加权迭代式(3)即可计算x-(0)。存在
| $ {{q}_{i}}(\xi )=(\xi -1)\sum\limits_{l=0}^{{{D}_{i}}}{\alpha _{l}^{(i)}}{{\xi }^{l}}, \alpha _{{{D}_{i}}}^{(i)}=1. $ | (4) |
下面介绍α(i)的一种分布式计算方法[13]。以勒贝格测度下为0的集合中的起始状态x0进行式(3)迭代(最多N次),组成如下Hankel矩阵
| $ \boldsymbol{H}(i, k):=\left[\begin{array}{cccc} y_{i}^{1} & y_{i}^{2} & \cdots & y_{i}^{k+1} \\ y_{i}^{2} & y_{i}^{3} & \cdots & y_{i}^{k+2} \\ \vdots & \vdots & & \vdots \\ y_{i}^{k+1} & y_{i}^{k+2} & \cdots & y_{i}^{2 k+1} \end{array}\right], $ |
其中
定理1(通过qi计算共识[8])当假设4,假设5满足且WT为行随机矩阵时,则共识可通过前Di次式(3)迭代得到,即
| $ \sum\limits_{i=0}^{{{D}_{i}}}{\hat{\alpha }_{l}^{(i)}}{{\boldsymbol{x}}_{i}}(l)=\frac{1}{N}\sum\limits_{i=1}^{N}{{{\boldsymbol{x}}_{i}}}(0), \hat{\alpha }_{l}^{(i)}=\frac{\alpha _{l}^{(i)}}{\sum\limits_{l=0}^{{{D}_{i}}}{\alpha _{l}^{(i)}}}. $ |
公式(4)中给出了αl(i)。
定理1给出了计算共识的方法,此方法是文中的信息融合的关键所在。
3 FTCHB算法设计结合FTC算法与重球法本章节提出算法1(finite-time-consensus-based heavy-ball method,FTCHB)。为避免二阶算法的巨大通信与计算量及经典梯度算法缓慢的收敛速率,本文决定结合使用历史信息的重球法以获取下降方向以求解问题(1)。重球法属于一阶算法,仅需要对梯度进行计算,避免了二阶算法计算量与通信量的缺陷。此外重球法在病态条件数的情况下可以保持良好的收敛速率。使用FTC算法辅助以达到共识。
|
|
算法初始化阶段各个节点分别计算自己FTC算法的相关参数α(i)(详见第2节)。算法中使用xi(t)表示节点i在内循环中第t步的状态,使用xck(i)表示节点i在第k次外循环迭代更新中状态。步骤2~步骤5可以理解为通过FTC算得初始状态的共识即
注意算法参数γk, βk选取方面各个节点使用相同的值,但参数值可通过FTC算法进行完全分布式计算。为简洁,算法表示仅通过表达式描述参数传递的过程。每次用到xj(t-1),
本节给出FTCHB算法的收敛性分析。注意到重球法中的更新方向单调下降方向,所以无法采用文献[10]中的方法进行分析。为分析收敛速率我们尝试通过找到一个Lyapunov函数以辅助收敛性证明。首先给出下降引理,并根据下降引理构造Lyapunov函数。此后在L-光滑与凸假设下得到一个目标函数F(x)有非各态历经的
注意到算法1中步骤3~步骤7以及步骤9~步骤12中更新是在每个内循环中使用FTC算法进行共识计算。这意味着对每次迭代k,有xck(i)=xck(j), ∀i,
上面的等价形式在证明中起着重要作用。算法1利用了变量复制后问题(2)的形式。下面通过FTC算法给出算法1的集中式等价解释。集中式理解方式允许我们参考重球法中的收敛性分析方法[14-15]。下面利用算法1主要迭代的等价形式结合文献[15]中的集中式处理分析方法获取非各态历经的收敛速率。
引理1 假设fi(x)是凸函数且一阶可导,且满足假设1,minF>-∞。假设动量系数{βk}k≥0⊆[0, 1)。通过选择步长
| $ {{\gamma }_{k}}=\frac{2\left( 1-{{\beta }_{k}} \right)e}{L}, $ |
其中:
| $ \begin{aligned} &{\left[F\left(\boldsymbol{x}_{c}^{k}\right)+\frac{\beta_{k}}{2 \gamma_{k}}\left\|\boldsymbol{x}_{c}^{k}-\boldsymbol{x}_{c}^{k-1}\right\|^{2}\right]-} \\ &{\left[F\left(\boldsymbol{x}_{c}^{k+1}\right)+\frac{\beta_{k+1}}{2 \gamma_{k+1}}\left\|\boldsymbol{x}_{c}^{k+1}-\boldsymbol{x}_{c}^{k}\right\|^{2}\right] \geqslant} \\ &\frac{(1-e) L}{2 e}\left\|\boldsymbol{x}^{k+1}-\boldsymbol{x}^{k}\right\|^{2}(>0), \end{aligned} $ |
证明:因为
| $ \boldsymbol{x}_{c}^{k+1}=\boldsymbol{x}_{c}^{k}-\gamma_{k} \nabla \boldsymbol{F}\left(\boldsymbol{x}_{c}^{k}\right)+\beta_{k}\left(\boldsymbol{x}_{c}^{k}-\boldsymbol{x}_{c}^{k-1}\right), $ | (5) |
在等价迭代式(5)及假设条件满足的情况下参考文献[15]中引理1的证明。
引理1说明
| $ V\left(\boldsymbol{x}_{c}^{k}\right):=F\left(\boldsymbol{x}_{c}^{k}\right)+\delta_{k}\left\|\boldsymbol{x}_{c}^{k}-\boldsymbol{x}_{c}^{k-1}\right\|^{2}-F^{*}, $ |
这里
| $ \begin{gathered} V\left(\boldsymbol{x}_{c}^{k}\right)-V\left(\boldsymbol{x}_{c}^{k+1}\right) \geqslant \frac{L(1-e)}{4 e} \times\left(\left\|\boldsymbol{x}_{c}^{k-1}-\boldsymbol{x}_{c}^{k}\right\|^{2}+\right. \\ \left.\left\|\boldsymbol{x}_{c}^{k}-\boldsymbol{x}_{c}^{k+1}\right\|^{2}\right) \geqslant 0, \end{gathered} $ |
这说明定义的V(xck)也是非增的函数。下面引理2给出V(xck)的上界在后面定理证明中起到关键作用。
引理2 假设引理1中的条件均满足,用
| $ \begin{align} & V{{\left( \boldsymbol{x}_{x}^{k} \right)}^{2}}\le {\epsilon_{k}}\left( V\left( \boldsymbol{x}_{c}^{k} \right)-V\left( \boldsymbol{x}_{c}^{k+1} \right) \right)\times \\ & \left( 2{{\left\| \boldsymbol{x}_{c}^{k}-\boldsymbol{x}_{c}^{k} \right\|}^{2}}+{{\left\| \boldsymbol{x}_{c}^{k}-\boldsymbol{x}_{c}^{k-1} \right\|}^{2}} \right), \\ \end{align} $ |
这里
证明:结合算法迭代更新的等价形式(5)及文献[15]中的引理2的证明可得。
由引理2可知V(xck)2 < +∞, 即supkV(xck) < +∞有上界。如果假设F为强制函数则有supk{‖xck‖}≤+∞。另外为了证明
| $ R: = \mathop {\sup }\limits_k\left\|\boldsymbol{x}_{c}^{k}-\boldsymbol{x}^{*}\right\|^{2}<+\infty, $ |
此处的
定理2 引理1中的假设成立的情况下,若0 < infkβk≤βk≤β0 < 1并且F(x)为强制函数,通过算法1,有
| $ F\left( \boldsymbol{x}_{c}^{k} \right)-{{F}^{*}}\le \frac{4R\mathop {{\rm{sup}}}\limits_k \left\{ {\epsilon _{k}} \right\}}{k}, $ |
证明:结合算法迭代更新的等价形式(5)及文献[15]定理1的证明可得。
注意这里的收敛是相对于算法外层的共识变量xck(即算法中的xck(i))的收敛,内层循环中的变量xi(l)并不能保证定理2中的收敛速率。
下面说明加上限制性强凸的假设之后,算法可以获得的非各态历经的线性收敛速率。
定理3 假设定理2中的条件均满足并且F满足假设2,那么有
| $ F\left( \boldsymbol{x}_{c}^{k} \right)-{{F}^{*}}\le V\left( \boldsymbol{x}_{c}^{0} \right){{\left( \frac{\ell }{1+\ell } \right)}^{k+1}}, $ |
这里
证明:结合算法迭代更新的等价形式(5)及文献[15]定理2的证明可得,注意对应文献[15]中的线性收敛速率常数应为
在限制性强凸的条件下有
本章节通过数值仿真体现FTCHB算法的有效性。图 1展现不同规模网络下的优越性,图 2展现不同问题参数下的性能。模型目标函数满足假设1,2,3均可以使用本文算法。常见的如最小二乘问题、机器学习问题、资源分配问题。本文的数值仿真考虑机器学习常见的岭回归问题[16],岭回归问题通过在目标函数中加入求解参数的正则项有效地处理了机器学习中的过拟合问题,因此得到广泛应用。在此问题中假设每个节点的目标函数为
| $ F(\boldsymbol{x})=\frac{N\lambda }{2}\|\boldsymbol{x}{{\|}^{2}}+\sum\limits_{i=1}^{N}{\sum\limits_{l=1}^{{{q}_{i}}}{\log }}\left[ 1+\exp \left( -{{v}_{il}}\boldsymbol{u}_{il}^{\text{T}}\boldsymbol{x} \right) \right], $ |
|
Download:
|
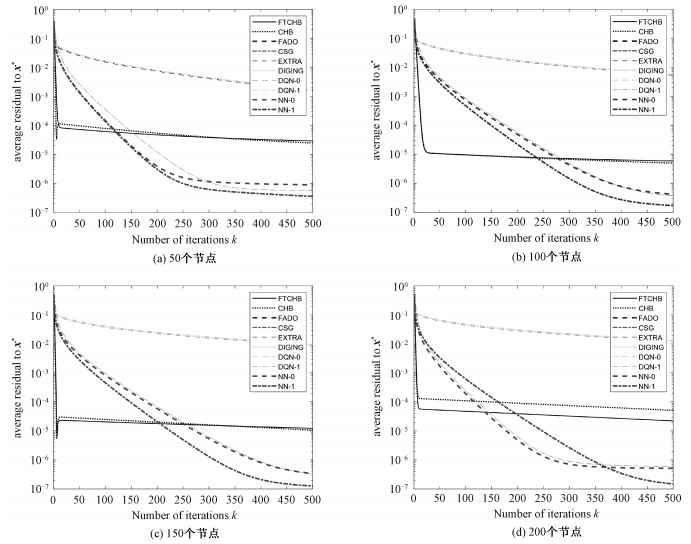
| 图 1 不同网络规模的收敛结果比较(λ=1) Fig. 1 Convergence result under different network sizes(λ=1) | |
|
Download:
|
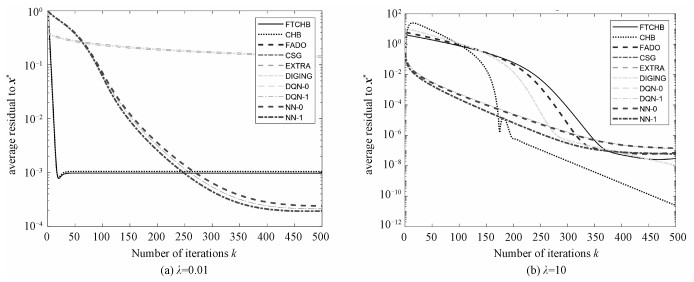
| 图 2 不同λ情况下收敛结果的比较(N=100) Fig. 2 Convergence result with different λ values(N=100) | |
其中:N为网络中节点的总数,λ>0为岭回归所对应的正则化参数,qi表示节点i上分配的数据个数,在此仿真中qi=6。uil表示节点i上的第l个数据,而vil∈{-1, +1}表示此数据对应的标签。在我们的仿真中随机生成数据
我们对比了一阶算法中的集中式的重球法(CHB)、FADO[9]、集中式的梯度下降法(CSG)、EXTRA[6]、DIGING[7]以及二阶算法中的DQN-0, 1[18],NN-0, 1[19]。图片中的横坐标为迭代次数,一次迭代表示进行一次节点变量xck(i)更新对应的计算,也即一次算法1的步骤7。这是因为在算法1中只有梯度计算为计算量大的操作,其他步骤仅为加权求和的线性操作。对于其他比较算法图中的横坐标增加1是一次方向更新。图片的纵坐标为网络中节点状态到最优解的残差平均值,即
从图 1,图 2可以看出除FTCHB外,相比其他一阶算法收敛比较接近,二阶算法之间的收敛也比较接近。与此同时FTCHB相对于其他一阶算法可以更快地收敛到更高的精度。二阶算法收敛最终收敛精度超过一阶算法。对比不同网络规模的情况,通过图 1可得知在网络规模变化的情况下FTCHB算法与其他算法的相对关系没有改变并且可以较快收敛到较高精度。从图 2可以看出当λ=10(对应条件数3.46×103)时所有算法表现均强于λ=0.01(对应条件数3.7×106),这可以看出条件数对一阶算法影响较大而对二阶算法影响较小。比较图 2(a)和2(b)两图可知FTCHB作为一阶算法在条件数大时可以很快收敛到较高精度。
此外,通过数值仿真可以看到设计算法的等价形式与集中式的重球法求解的最优值相差无几。两者有一定差别的主要原因是在算法初始化步骤1过程中的计算误差,如何减小此误差是一个单独的开放问题。
6 总结本文提出一种解决基于共识的多智体系统协同优化问题的分布式算法FTCHB。通过结合FTC及重球法,在凸假设和L-光滑假设下可以达到
| [1] |
Beck A, Nedić A, Ozdaglar A, et al. An O(1/k) gradient method for network resource allocation problems[J]. IEEE Transactions on Control of Network Systems, 2014, 1(1): 64-73. Doi:10.1109/TCNS.2014.2309751 |
| [2] |
Rabbat M, Nowak R. Distributed optimization in sensor networks[C]//Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks 2004. April 26-27, 2004. Berkeley, California, USA. New York: Association for Computing Machinery, 2004: 20-27.
|
| [3] |
Shamma J S. Cooperative control of distributed multi-agent systems[M]. New York: John Wiley & Sons, Ltd, 2007.
|
| [4] |
Wai H T, Yang Z, Wang Z, et al. Multi-agent reinforcement learning via double averaging primal-dual optimization[C]//Bengio S, Wallach H, Larochelle, et al. Advances in Neural Information Processing Systems 31: New York: Curran Associates, 2018: 9649-9660.
|
| [5] |
Nedic A, Ozdaglar A. Distributed subgradient methods for multi-agent optimization[J]. IEEE Transactions on Automatic Control, 2009, 54(1): 48-61. Doi:10.1109/TAC.2008.2009515 |
| [6] |
Shi W, Ling Q, Wu G, et al. EXTRA: an exact first-order algorithm for decentralized consensus optimization[J]. SIAM Journal on Optimization, 2015, 25(2): 944-966. Doi:10.1137/14096668X |
| [7] |
Nedić A, Olshevsky A, Shi W. Achieving geometric convergence for distributed optimization over time-varying graphs[J]. SIAM Journal on Optimization, 2017, 27(4): 2597-2633. Doi:10.1137/16M1084316 |
| [8] |
Sundaram S, Hadjicostis C N. Finite-time distributed consensus in graphs with time-invariant topologies[C]//2007 American Control Conference, July 9-13, 2007, New York NY, USA. IEEE, 2007: 711-716.
|
| [9] |
Mai V S, Abed E H. Local prediction for enhanced convergence of distributed optimization algorithms[J]. IEEE Transactions on Control of Network Systems, 2018, 5(4): 1962-1975. Doi:10.1109/TCNS.2017.2776084 |
| [10] |
Qu Z H, Wu X Y, Lu J. Finite-time-consensus-based methods for distributed optimization[C]//2019 Chinese Control Conference (CCC). July 27-30, 2019, Guangzhou, China. IEEE, 2019: 5764-5769.
|
| [11] |
Xiao L, Boyd S. Fast linear iterations for distributed averaging[J]. Systems & Control Letters, 2004, 53(1): 65-78. |
| [12] |
Horn R A, Johnson C R. Matrix analysis[M]. 2nd ed. Cambridge: Cambridge University Press, 1985: 191-200.
|
| [13] |
Sundaram S, Hadjicostis C N. Distributed function calculation and consensus using linear iterative strategies[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(4): 650-660. Doi:10.1109/JSAC.2008.080507 |
| [14] |
Ghadimi E, Feyzmahdavian H R, Johansson M. Global convergence of the heavy-ball method for convex optimization[C]//2015 European Control Conference (ECC). July 15-17, 2015, Linz, Austria. IEEE, 2015: 310-315.
|
| [15] |
Sun T, Yin P H, Li D S, et al. Non-ergodic convergence analysis of heavy-ball algorithms[C]//Proceedings of the AAAI Conference on Artificial Intelligence. AAAI, 2019, 33(1): 5033-5040.
|
| [16] |
Murphy K P. Machine learning: a probabilistic perspective[M]. Cambridge, Massachusetts: MIT press, 2012: 290-295.
|
| [17] |
Löfberg J. YALMIP: a toolbox for modeling and optimization in MATLAB[C]//2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No. 04CH37508). September 2-42004, Taipei, Taiwan, China. IEEE, 2004: 284-289.
|
| [18] |
Bajović D, Jakovetić D, Krejić N, et al. Newton-like method with diagonal correction for distributed optimization[J]. SIAM Journal on Optimization, 2017, 27(2): 1171-1203. Doi:10.1137/15M1038049 |
| [19] |
Mokhtari A, Ling Q, Ribeiro A. Network Newton distributed optimization methods[J]. IEEE Transactions on Signal Processing, 2017, 65(1): 146-161. Doi:10.1109/TSP.2016.2617829 |
 2022, Vol. 39
2022, Vol. 39 


