由于传感器空间分辨率和地面物体多样性的限制,混合像元问题广泛存在于高光谱遥感数据中。因此,混合像元分解已成为高光谱图像分析的最重要步骤之一。在线性混合模型下,混合像元是相应的丰度系数加权的几个单一光谱特征(称为端元)的线性组合。
在线性混合模型的假设下,端元提取算法可以分为端元选择和端元生成两类[1]。端元选择算法假设数据集中存在恰好为端元的像元,通过一定方法将最有可能成为单形体顶点的像元选择出来。比如纯像元指数算法(pixel purity index,PPI)[2],NFINDR[3],以光谱信息熵改进的NFINDR[4],单形体膨胀算法(simplex growing algorithm, SGA)[5],顶点分析法(vertex component analysis, VCA)[6],高斯消去法(Gaussian elimination method, GEM)[7],基于Gram行列式的快速端元确定法(fast gram determinant based algorithm, FGDA)[8],基于显著性的端元检测(saliency-based endmember detection, SED)[9],基于K-means聚类的端元提取[10]等。除此之外高光谱图像的聚类也可用于端元选择,譬如谱聚类[11]。当然对于实际的高光谱数据集,纯像元可能是不存在的,为了解决这种情况新的端元生成算法应运而生。端元生成算法在本质上就是找到尽可能包含所有像元的体积最小的单形体。譬如最小体积转换算法(minimum volume transformation, MVT)[12],迭代约束端元算法(the iterative constrained endmember method, ICE)[13],稀疏性ICE(sparsity-promoting ICE, SPICE)[14],基于非负矩阵分解的最小体积约束算法(minimum volume constraint NMF, MVC-NMF)[15], 最小封闭单形体体积(minimum volume enclosing simplex, MVES)[16-17]等,以及本文提到的几何优化模型(the geometric optimization model, GOM)[18]。
在不满足纯像元条件下,现有的端元生成方法一般通过使重建误差最小化来得到最终的端元。但是在实际的高光谱图像中一般是存在噪声的,噪声的存在会污染原有的像元,使得最小化重建误差的提取结果过拟合,失去其应有的物理意义。因此很多端元生成方法都引入了一些约束(例如体积约束)来限制过拟合。事实上,单形体体积的最小化本就是端元特征的体现。我们发现可以通过约束重建误差不变以得到更小的单形体体积。重建误差的大小与噪声强度是正相关的,以重建误差作为约束会有更好的鲁棒性。基于此提出基于固定模型误差的最优单形体体积模型,旨在对端元提取的结果进一步优化。
1 背景知识线性混合模型认为高光谱图像可以看成丰度矩阵与端元的线性组合加上误差,线性混合模型满足以下关系
| $ \mathit{\boldsymbol{X}} = \sum\limits_{i = 1}^p {{\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{S}}_i} + \mathit{\boldsymbol{n}}} = \mathit{\boldsymbol{AS}} + \mathit{\boldsymbol{n}}, $ | (1) |
其中:X为l (l为影像波段数)维混合像元光谱,是已知观测量;A为l×p(p为端元数目)端元矩阵或源矩阵,其中每一列为一个端元的光谱向量;丰度矩阵S为该像元对应各个端元的丰度;n为l维高斯随机噪声或模型误差。对于线性光谱混合模型,丰度矩阵S中的每个向量满足2个限制条件:非负性限制(abundance non-negativity constraint, ANC)、和为1限制(abundance sum-to-one constraint, ASC), 即每个像元的丰度系数均大于0且和为1。
给定端元矩阵A与丰度矩阵S,重建误差可以表示为
| $ \varepsilon = \left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{AS}}} \right\|_F^2. $ | (2) |
使用V表示单形体体积,统一地看,端元提取的最终目的均是优化如下目标函数
| $ {\rm{min}}F(\mathit{\boldsymbol{A, S, }}\lambda ) = {\rm{min}}\left( {\frac{1}{2}\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{AS}}} \right\|_F^2 + \lambda V(\mathit{\boldsymbol{A}})} \right). $ | (3) |
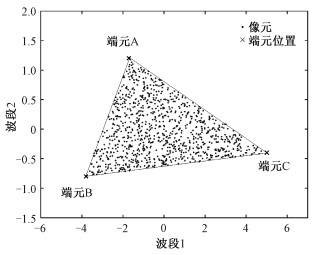
这里介绍一下凸面几何体理论,凸面几何体理论是高光谱影像端元提取的理论基础。如果空间中任意2点的连线仍然在该几何体内,那么该几何体就是凸的。n维凸面几何体是由n-1维的凸集构成,而单形体是指n维空间中只有n+1个顶点的凸面几何体。图 1是在2个波段的情况下,所有像元组成了一个三角形。A、B、C 3点是该凸面几何体的顶点,即该影像的纯像元位置;混合像元则分布在三角形的内部,每个像元均可以由3点线性表示。光谱矢量位于单形体内,如果线性混合模型的所有假设成立,那么其顶点就是要找的端元,端元提取相当于识别该单形体的顶点。
|
Download:
|
| 图 1 单形体(顶点代表端元) Fig. 1 Simplex vertices representing endmembers | |
最小化重建误差的意义是为了满足和为1约束与非负性约束;体积约束是为了单形体更紧密地包含像元,从而使得端元提取结果有物理意义。在理想条件下,纯像元存在、噪声忽略不计,那么重建误差项为0,这种情况下端元选择例如NFINDR、PPI等算法就可以准确定位端元位置。在非理想条件下需要考虑噪声对高光谱图像的污染与纯像元不存在的情况。而端元选择算法无法兼顾所有的约束条件,仅仅将已有的像元作为提取结果,导致端元提取结果不准确。
端元生成算法(例如MVC-NMF)为了弥补上述算法的缺陷,同时考虑重建误差与体积的约束,但是对于式(3)中参数λ的选择没有判据,生成结果的好坏极大程度地依赖λ的选择。
2 固定模型误差优化单形体体积 2.1 几何优化模型(GOM)几何优化模型利用一种新的衡量重建误差的方式,它放弃了线性混合模型中同时使用端元矩阵与丰度系数表示重建误差的方式,而是采用只有单一变量端元矩阵A来表示重建误差。
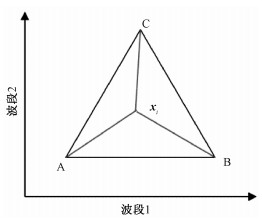
如图 2所示,一幅高光谱图像端元矩阵为A,端元数量为p,图中任一像元xi的丰度系数si可以写成
| $ {s_i} = \left[ {\frac{{V({\mathit{\boldsymbol{A}}_{i1}})}}{{V\left( \mathit{\boldsymbol{A}} \right)}}, \frac{{V({\mathit{\boldsymbol{A}}_{i2}})}}{{V\left( \mathit{\boldsymbol{A}} \right)}}, \frac{{V({\mathit{\boldsymbol{A}}_{i3}})}}{{V\left( \mathit{\boldsymbol{A}} \right)}}, \ldots , \frac{{V({\mathit{\boldsymbol{A}}_{ip}})}}{{V(\mathit{\boldsymbol{A}})}}} \right], $ | (4) |
|
Download:
|
| 图 2 几何优化模型 Fig. 2 Geometric optimization model | |
其中:
| $ {\mathit{\boldsymbol{A}}_{ij}} = \left[ {{\mathit{\boldsymbol{a}}_1}, \ldots , {\mathit{\boldsymbol{a}}_{j - 1}}, {\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{a}}_{j + 1}}, \ldots , {\mathit{\boldsymbol{a}}_p}} \right], $ |
其几何意义为将端元矩阵A中第i个端元换为xi后重新计算的端元矩阵的体积。
可以证明,当像元xi位于由端元构造的单形体内时,从式(4)推导出的点xi的体积比的系数总和恰好为1。实际上,可以发现对于任意单形体体内的像元xi,均满足
| $ \left( {\sum\limits_{j = 1}^p {\frac{{V\left( {{\mathit{\boldsymbol{A}}_{ij}}} \right)}}{{V\left( \mathit{\boldsymbol{A}} \right)}}} } \right) - 1 = 0. $ | (5) |
反之,如果像元xi在单形体外部,那么应该满足
| $ \left( {\sum\limits_{j = 1}^p {\frac{{V\left( {{\mathit{\boldsymbol{A}}_{ij}}} \right)}}{{V\left( \mathit{\boldsymbol{A}} \right)}}} } \right) - 1 > 0. $ | (6) |
于是重建误差可以表示为
| $ \varepsilon = \frac{1}{M}\sum\limits_{i = 1}^M {\left( {\left( {\sum\limits_{j = 1}^p {\frac{{V\left( {{\mathit{\boldsymbol{A}}_{ij}}} \right)}}{{V\left( \mathit{\boldsymbol{A}} \right)}}} } \right) - 1} \right)} , $ | (7) |
其中:M是像元的数量,p是端元数量。
GOM的关键优势在于它只有1个变量,即端元矩阵A,因此它避免了由于丰度矩阵S引起的所有问题。
2.2 EIC-OSV的建立及求解单形体体积在端元提取中具有重要的物理意义。端元提取实际上是在单形体体积的最小化与重建误差的最小化之间取得平衡。本文选择约束重建误差不变来获取最优的体积,这样有2个优势:一是重建误差有理想值0,规避了初值选取问题;二是保证了单形体体积不被约束,从而使求解结果有物理意义。基于这个思路可以建立如下EIC-OSV模型:
| $ \left\{ \begin{array}{l} {\rm{min}}h\left( \mathit{\boldsymbol{A}} \right) = {\rm{min}}V\left( \mathit{\boldsymbol{A}} \right), \\ {\rm{s}}.{\rm{t}}.\varepsilon \left( \mathit{\boldsymbol{A}} \right) = \frac{1}{M}\sum\limits_{i = 1}^M {\left( {\sum\limits_{j = 1}^p {V\left( {{\mathit{\boldsymbol{A}}_{ij}}} \right) - V\left( \mathit{\boldsymbol{A}} \right)} } \right)} = {\varepsilon _0}. \end{array} \right. $ | (8) |
该模型根据拉格朗日乘子法可以转化为如下无约束优化问题:
| $ \left\{ \begin{array}{l} {\rm{min}}H\left( {\mathit{\boldsymbol{A}}, \lambda } \right)\\ = {\rm{min}}\left( {V\left( \mathit{\boldsymbol{A}} \right) + \lambda \left( {\varepsilon \left( \mathit{\boldsymbol{A}} \right) - {\varepsilon _0}} \right)} \right) \end{array} \right., $ | (9) |
其中:ε0为重建误差的初值,在无噪声时为0,考虑噪声时为某一固定值。为保证重建误差约束,需要满足目标函数H的导数与重建误差函数的导数互相垂直,即两者的内积为0:
| $ \left\langle {{{H'}_\mathit{\boldsymbol{A}}}\left( {\mathit{\boldsymbol{A}}, \lambda } \right), \varepsilon ' \left( \mathit{\boldsymbol{A}} \right)} \right\rangle = 0, $ | (10) |
式(10)等价于
| $ \left\langle {V' \left( \mathit{\boldsymbol{A}} \right) + \lambda \varepsilon ' (\mathit{\boldsymbol{A}}), \varepsilon ' (\mathit{\boldsymbol{A}})} \right\rangle = 0, $ | (11) |
其中:
| $ \begin{array}{l} V' \left( \mathit{\boldsymbol{A}} \right) = {\left[ {\frac{1}{{\left( {p - 1} \right)!}}{\rm{abs}}\left( {{\rm{det}}\left( {\mathit{\boldsymbol{\bar A}}} \right)} \right){{\left( {{{\mathit{\boldsymbol{\bar A}}}^{ - 1}}} \right)}^{\rm{T}}}} \right]_{1:p - 1, 1:p}}, \\ \mathit{\boldsymbol{\bar A}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}\\ {\mathit{\boldsymbol{1}}_p^{\rm{T}}} \end{array}} \right]. \end{array} $ |
那么λ就可以根据重建误差约束求解:
| $ \lambda = - \frac{{\left\langle {V' \left( \mathit{\boldsymbol{A}} \right), \varepsilon ' \left( \mathit{\boldsymbol{A}} \right)} \right\rangle }}{{\left\langle {\varepsilon ' \left( \mathit{\boldsymbol{A}} \right), \varepsilon ' \left( \mathit{\boldsymbol{A}} \right)} \right\rangle }}, $ | (12) |
其中:
| $ \begin{array}{l} \varepsilon ' \left( \mathit{\boldsymbol{A}} \right) = \frac{1}{M}\sum\limits_{i = 1}^M {\left( {\sum\limits_{j = 1}^p {V\left( {{\mathit{\boldsymbol{A}}_{ij}}} \right) - V\left( \mathit{\boldsymbol{A}} \right)} } \right)'} \\ = \frac{1}{M}\sum\limits_{i = 1}^M {\left( {\sum\limits_{j = 1}^p {V'\left( {{\mathit{\boldsymbol{A}}_{ij}}} \right) - V'\left( \mathit{\boldsymbol{A}} \right)} } \right)} . \end{array} $ |
求解方法选用梯度下降法。考虑到求解过程需要一直保证重建误差空间与目标函数空间正交,因此每一步迭代都需要求解一次λ,每次更新λ之后,利用下式迭代更新端元矩阵A:
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{A}} - \eta {H'_A}\left( {\mathit{\boldsymbol{A}}, \lambda } \right). $ | (13) |
其中η为步长。步长的选择在该优化模型中至关重要,如果步长足够小,则可以保证每一次迭代都减少,但可能导致收敛太慢;如果步长太大,则不能保证每一次迭代都减少,也不能保证收敛。最终的求解结果需要多次迭代直至目标函数的变化小于一定阈值。EIC-OSV的本质是在重建误差梯度的正交补空间进一步缩小端元体积。只要两者梯度不是严格平行的,端元体积存在可以下降的梯度方向,就可以利用EIC-OSV进行迭代优化。
2.3 信噪比与重建误差的关系在不考虑噪声时,如果能够准确地找到端元,那么也可以准确地实现重建误差为0。然而一般情况下,完全理想的高光谱图像是不存在的,在有噪声干扰时,即使找到的端元是完美的真实端元,图像的重建误差仍然存在。
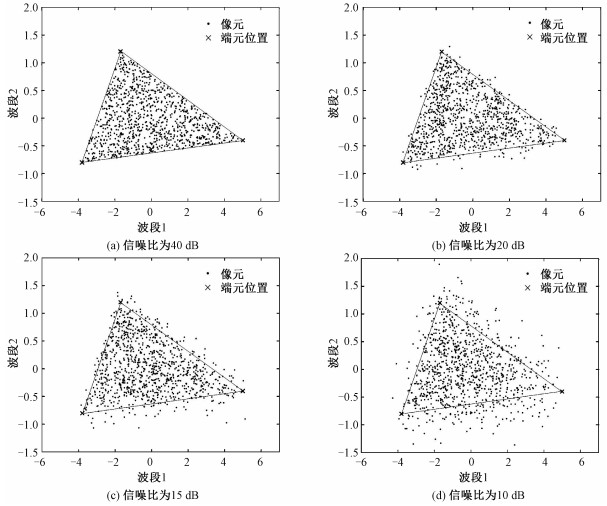
图 3列举了添加4种不同幅度噪声(信噪比依次为40、20、15、10dB)后的像元分布情况。理想数据在添加不同程度的噪声之后,各个像元的分布在各个方向有不同的波动,很多像元落在真实端元围成的单形体外,因此几何优化模型的重建误差不为0。噪声越大,落在单形体外的像元数量越多,距离越远。
|
Download:
|
| 图 3 不同信噪比下的像元分布 Fig. 3 Pixel distribution under different SNRs | |
接下来讨论对于给定信噪比的高光谱图像,如何在端元提取中降低噪声的影响。对无噪声的数据,可以约束重建误差为0;对有噪声的数据,可以采取如下措施:
1) 根据给定的高光谱图像的信噪比、波段数、分辨率、像元个数、端元数量等已有条件,判断在这一系列条件下真实端元的重建误差。
2) 选择合适的端元矩阵,使其重建误差等于步骤1)中的重建误差,将该端元矩阵作为初始端元矩阵,利用EIC-OSV模型进行端元优化。下面给出EIC-OSV实现的具体流程:
|
|
在该测试中,使用来自美国地质调查局数字光谱库的3个参考图:明矾石、方解石和高岭石,生成具有1000个像元的混合数据。通过Dirichlet分布(参数[1/3, 1/3, 1/3])产生相应的丰度系数。为了验证不同条件下的算法提取效果,对这组数据分别作2种处理:舍弃丰度系数大于0.9的像元(为了保证不满足纯像元条件);在前者基础上增加SNR=15dB的高斯白噪声(为了评估算法在噪声方面的性能)。
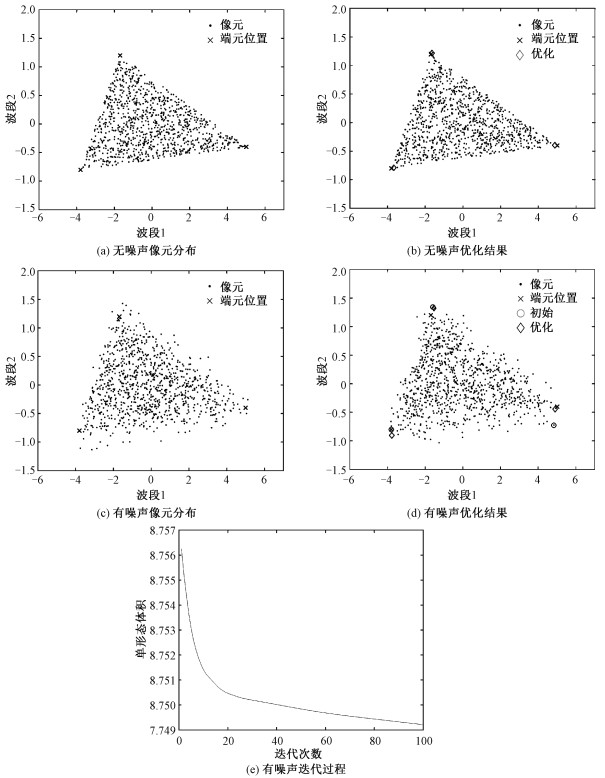
如图 4(a),对于不存在噪声的理想情况,可以用一个足够大的单形体作为初值,重建误差约束为0,EIC-OSV就可以精准地生成端元,优化结果如图 4(b)所示。
|
Download:
|
| (a)(b)为“纯像元不存在”情况; (c)(d)(e)为“加入SNR = 15 dB噪声”情况 图 4 优化结果 Fig. 4 Optimized results | |
不同信噪比的不同分布情况,已经在图 3中给出。随着噪声强度的扩大,真正的端元围成的单形体舍弃的噪声点逐渐增多。可以约束重建误差等于该信噪比下的某一固定值,优化单形体体积。这样得到的单形体体积具有物理意义。
以加入信噪比为15dB的噪声为例,假设端元已知,多次生成固定信噪比的随机数据,统计信噪比与模型误差的关系。统计了1000组数据下的重建误差,其均值为0.0151,标准差为0.0013,重建误差对于该组数据分布较为稳定。事实上如果像元数量足够大,重建误差会趋于某个固定的值。如图 4(c)所示,给定一组已知信噪比为15dB的待测数据。根据NFINDR的端元提取结果作为初始单形体,维持该单形体质心不变进行膨胀或者缩小,利用二分法多次确定某一初始端元矩阵使得其模型误差约为0.0151,利用得到的端元矩阵作为初值进行迭代优化。优化后的端元提取结果如图 4(d)所示。可以看出优化结果几乎完全地契合了真实端元。图 4(e)反映了单形体体积与迭代次数的关系。随着迭代次数的增加,单形体体积也在不断减小,符合我们的期望。
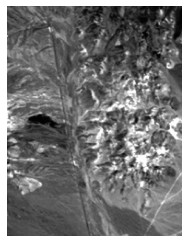
3.2 真实数据验证本节使用真实的高光谱数据集进一步验证EIC-OSV的有效性。该数据是1997年6月19日在内华达州的铜矿开采场由机载可见光红外光谱仪(AVIRIS)拍摄。本次实验中使用的子数据如图 5所示。该数据包含370~2500nm范围内的总共224个波段。考虑到存在水蒸气吸收或低信噪比的情况,删除了波段1~3、107~113、153~169、221~224。
|
Download:
|
| 图 5 实验用数据 Fig. 5 Experimental data | |
根据虚拟维度(virtual dimension,VD)[19]以及实地的地面调查[20], 提取端元数量设置为14。真实端元的光谱通过ENVI软件中USGS数字光谱库中对相应的光谱重采样获得。实验中,首先使用PCA将数据降至13维,分别利用NFINDR、ICE、MVC-NMF提取14个端元,同时分别将这3种算法提取的端元矩阵作为EIC-OSV的初值,计算各自的重建误差并进行优化。这样可以大大减少迭代次数,方便选取迭代步长。
使用均方根角度误差(rmsSAE)来衡量端元提取结果的准确性。rmsSAE反映了提取端元与真正端元的均方角度差异,定义如下:
| $ {\rm{rmsSAE}} = \sqrt {\frac{1}{p}\sum\limits_{i = 1}^p {{\rm{SAE}}_i^2} } , $ | (14) |
其中
| $ {\rm{SA}}{{\rm{E}}_i} = {\rm{arccos}}\left( {\frac{{\mathit{\boldsymbol{e}}_i^{\rm{T}}{{\mathit{\boldsymbol{\hat e}}}_i}}}{{\left\| {{\mathit{\boldsymbol{e}}_i}} \right\| \cdot \left\| {{{\mathit{\boldsymbol{\hat e}}}_i}} \right\|}}} \right). $ |
其物理意义为单一提取端元与真实端元之间的角度。
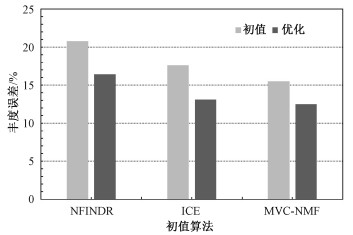
表 1给出了端元提取的结果与真实端元之间的角度、均方根角度误差。利用已经提取到的端元,可以分别计算对应的丰度矩阵以验证精度,其丰度误差在图 6中给出。
|
|
表 1 端元提取光谱角度差 Table 1 Endmember extraction spectral angle error |
|
Download:
|
| 图 6 丰度误差对比 Fig. 6 Abundance error comparison | |
对比以上实验结果,模拟数据的端元提取结果符合预期:当不考虑噪声或者噪声的影响极小时,约束重建误差为0,EIC-OSV可以作为一种理想数据的端元生成算法;在有噪声影响时,相同端元矩阵对于固定信噪比的随机数据,重建误差在统计上是大致稳定的,将该统计值作为EIC-OSV的初值进行优化,提取结果几乎完全吻合于真实端元。这也体现了EIC-OSV的一个显著优势:它的约束值——重建误差与噪声强度是正相关的,当确定这个约束值之后进行优化,能极大限度地规避噪声带来的影响。
真实数据的实验中,对比表 1的各组数据。可以发现3种初始方案中NFINDR的提取结果较差,这可能是图像中不存在纯像元导致的,而ICE、MVC-NMF均考虑了纯像元不存在的情况。对于这3种不同的初始方案,无论是rmsSAE还是丰度误差,EIC-OSV均实现了优于初值的提取结果。而且对于更好的初值,最终的优化结果也更接近真实端元,这也意味着该初值对应的ε0更接近真实值。值得注意的是,EIC-OSV的优化目标为整个端元矩阵的单形体体积,因此并不是所有端元的提取结果都会得到改善。
由于仪器参数的不确定,可用数据集受限以及实地考察结果的真实性,并不能完美地拟合初始重建误差。但考虑到EIC-OSV是在重建误差梯度的正交补空间进一步迭代缩小端元体积,其优化目标总是迫使迭代结果更加逼近真实端元的方向。因此理论上EIC-OSV可以对现有的所有端元提取算法进行优化,只要目标函数梯度与模型误差梯度不平行,就可以通过EIC-OSV优化得到更小的单形体体积,使得噪声对端元提取结果的影响降到最低,从而保证端元提取结果更有物理意义。
4 结论随着遥感技术的快速发展,高光谱图像的应用范围越来越广,混合像元问题普遍存在于高光谱数据中。作为混合像元分析的重要步骤,端元提取算法侧重于最小化重建误差来提升端元提取的精度,无法解决噪声带来的过拟合问题。本文提出的EIC-OSV模型沿用几何优化模型的重建误差,避开了求解丰度系数矩阵的繁琐步骤。针对重建误差的约束来最小化单形体体积,将信噪比与重建误差建立关联,保障在噪声条件下求解的结果仍然具有物理意义。在模拟数据及真实数据的提取结果均表现良好。对于真实数据,本文实现了提取结果的优化,如果要获得更理想的结果需要定量探讨信噪比与重建误差的关系,以及其他因素比如端元数量、像元数量、丰度分布等因素的影响,这也是将来工作致力的方向。
| [1] |
李二森, 朱述龙, 周晓明, 等. 高光谱图像端元提取算法研究进展与比较[J]. 遥感学报, 2011, 15(4): 659-679. |
| [2] |
Boardman J W. Automating spectral unmixing of AVIRIS data using convex geometry concepts[J]. Summaries of the Fourth Annual JPL Airborne Geoscience Workshop, JPL Publication, 1993, 1: 11-14. |
| [3] |
Winter M E. N-FINDR: an algorithm for fast autonomous spectral end-member determination in hyperspectral data[C]//International Symposium on Optics Science, Engineering, and Instrumentation. Proc SPIE 3753, Imaging Spectrometry V, Denver, CO, USA. 1999, 3753: 266-275.
|
| [4] |
杨可明, 魏华锋, 刘飞, 等. 以光谱信息熵改进的N-FINDR高光谱端元提取算法[J]. 地球信息科学学报, 2015, 17(8): 979-985. |
| [5] |
Chang C I, Wu C C, Liu W, et al. A new growing method for simplex-based endmember extraction algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(10): 2804-2819. Doi:10.1109/TGRS.2006.881803 |
| [6] |
Nascimento J M P, Dias J M B. Vertex component analysis: a fast algorithm to unmix hyperspectral data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 898-910. Doi:10.1109/TGRS.2005.844293 |
| [7] |
Geng X R, Xiao Z Q, Ji L Y, et al. A Gaussian elimination based fast endmember extraction algorithm for hyperspectral imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 79: 211-218. Doi:10.1016/j.isprsjprs.2013.02.020 |
| [8] |
Sun K, Geng X R, Wang P S, et al. A fast endmember extraction algorithm based on gram determinant[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(6): 1124-1128. Doi:10.1109/LGRS.2013.2288093 |
| [9] |
Wang X Y, Zhong Y F, Xu Y, et al. Saliency-based endmember detection for hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(7): 3667-3680. Doi:10.1109/TGRS.2018.2805340 |
| [10] |
严阳, 华文深, 崔子浩, 等. 高光谱分类体积的端元提取[J]. 激光与光电子学进展, 2018, 55(9): 446-451. |
| [11] |
杨随心, 耿修瑞, 杨炜暾, 等. 一种基于谱聚类算法的高光谱遥感图像分类方法[J]. 中国科学院大学学报, 2019, 36(2): 267-274. |
| [12] |
Craig M D. Minimum-volume transforms for remotely sensed data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(3): 542-552. Doi:10.1109/36.297973 |
| [13] |
Berman M, Kiiveri H, Lagerstrom R, et al. ICE: a statistical approach to identifying endmembers in hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(10): 2085-2095. Doi:10.1109/TGRS.2004.835299 |
| [14] |
Zare A, Gader P. Sparsity promoting iterated constrained endmember detection in hyperspectral imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(3): 446-450. |
| [15] |
Miao L D, Qi H R. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(3): 765-777. Doi:10.1109/TGRS.2006.888466 |
| [16] |
Hendrix E M T, Garcia I, Plaza J, et al. A new minimum-volume enclosing algorithm for endmember identification and abundance estimation in hyperspectral data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(7): 2744-2757. Doi:10.1109/TGRS.2011.2174443 |
| [17] |
Chan T H, Chi C Y, Huang Y M, et al. A convex analysis-based minimum-volume enclosing simplex algorithm for hyperspectral unmixing[J]. IEEE Transactions on Signal Processing, 2009, 57(11): 4418-4432. Doi:10.1109/TSP.2009.2025802 |
| [18] |
Geng X R, Ji L Y, Zhao Y C, et al. A new endmember generation algorithm based on a geometric optimization model for hyperspectral images[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 811-815. Doi:10.1109/LGRS.2012.2224635 |
| [19] |
Chang C I, Du Q. Estimation of number of spectrally distinct signal sources in hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(3): 608-619. Doi:10.1109/TGRS.2003.819189 |
| [20] |
Swayze G, Clark R N, Kruse F, et al. Ground-truthing AVIRIS mineral mapping at Cuprite, Nevada[C]//Summaries of the Third Annual JPL Airborne Geoscience Workshop. Denver, CO: JPL Publication, 1992: 47-49.
|
 2022, Vol. 39
2022, Vol. 39 


